M e c c ani c a / M O T O T R A S L AT O R I O
UE1030260
Moto uniformemente accelerato
UE1030260
B A SI GE NE R A L I
La velocità istantanea v e l’accelerazione istantanea a di un punto materiale sono definiti come rispettivamente la derivata prima e la derivata
seconda dello spostamento s rispetto al tempo t. Queste definizioni possono essere riprodotte in modo sperimentale considerando invece delle
derivate i relativi rapporti incrementali, e misurando i tempi tn relativi
ai punti del percorso sn considerando piccoli incrementi dello spostamento. Vengono così creati i presupposti, per esempio, per analizzare a
livello sperimentale l’andamento cronologico del moto uniformemente
accelerato.
Con un’accelerazione costante a la velocità istantanea v aumenta in modo
proporzionale al tempo t; assumendo il punto materiale inizialmente
fermo:
(1)
v = a ⋅t
Lo spostamento s aumenta in modo proporzionale al quadrato del tempo:
(2)
F UN Z IONI
SCOPO
• Registrazione dello spostamento in
funzione del tempo.
• Determinazione della velocità istantanea in funzione del tempo.
• Determinazione dell’accelerazione
istantanea in funzione del tempo.
• Determinazione dell’accelerazione
media come parametro di adattamento
e confronto con il quoziente ricavato
dalla forza e dalla massa.
Registrazione e valutazione di movimenti moti uniformemente accelerati sulla rotaia delle
pulegge­
1
s = ⋅a ⋅t 2
2
RIASSUNTO
In un moto uniformemente accelerato, la velocità istantanea è lineare rispetto al tempo e lo spostamento ha un rapporto quadratico rispetto ad esso. Queste dipendenze sono analizzate nell’esperimento sui moti sulla rotaia delle pulegge, che vengono registrati con una combinazione di una puleggia
Super Pulley e di una fotocellula.
A pparec chi nec essari
F
a=
m
Numero Apparecchio
Queste dipendenze sono esaminate nell’esperimento con un carrello sulla
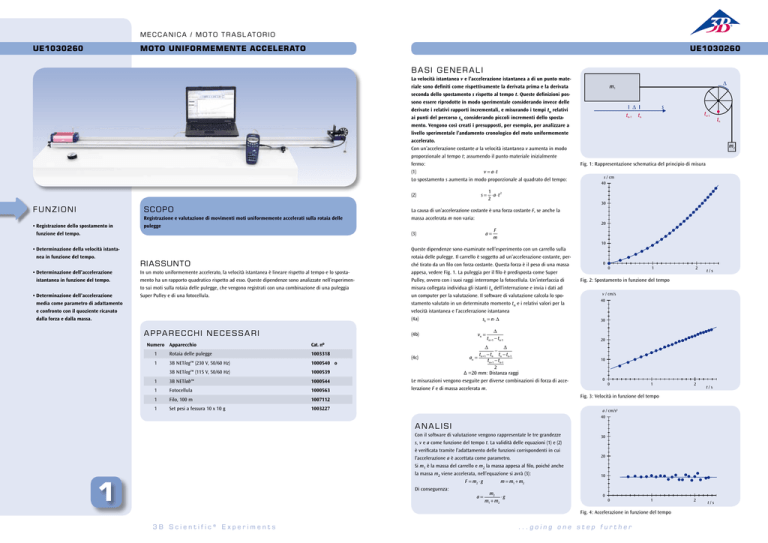
rotaia delle pulegge. Il carrello è soggetto ad un’accelerazione costante, perché tirato da un filo con forza costante. Questa forza è il peso di una massa
appesa, vedere Fig. 1. La puleggia per il filo è predisposta come Super
Pulley, ovvero con i suoi raggi interrompe la fotocellula. Un’interfaccia di
misura collegata individua gli istanti tn dell’interruzione e invia i dati ad
un computer per la valutazione. Il software di valutazione calcola lo spostamento valutato in un determinato momento tn e i relativi valori per la
velocità istantanea e l’accelerazione istantanea
(4a)
sn = n⋅ Δ
(4b)
Cat. no
1
Rotaia delle pulegge
1003318
1
3B NETlog™ (230 V, 50/60 Hz)
1000540o
3B NETlog™ (115 V, 50/60 Hz)
1000539
1
3B NETlab™
1000544
1
Fotocellula
1000563
1
Filo, 100 m
1007112
1
Set pesi a fessura 10 x 10 g
1003227
vn =
tn-1
tn
s
tn-1
Δ
tn+1 − tn-1
Fig. 1: Rappresentazione schematica del principio di misura
s / cm
40
20
10
0
0
1
2
t/s
Fig. 2: Spostamento in funzione del tempo
v / cm/s
40
30
20
Δ
Δ
−
tn+1 − tn tn − tn-1
(4c)
an =
tn+1 − tn-1
2
Δ =20 mm: Distanza raggi
Le misurazioni vengono eseguite per diverse combinazioni di forza di accelerazione F e di massa accelerata m.
10
0
0
1
2
t/s
Fig. 3: Velocità in funzione del tempo
a / cm/s²
40
A N A L ISI
Con il software di valutazione vengono rappresentate le tre grandezze
s, v e a come funzione del tempo t. La validità delle equazioni (1) e (2)
è verificata tramite l’adattamento delle funzioni corrispondenti in cui
l’accelerazione a è accettata come parametro.
Si m1 è la massa del carrello e m2 la massa appesa al filo, poiché anche
la massa m2 viene accelerata, nell’equazione si avrà (3):
F = m2 ⋅ g
m = m1 + m2
1
Di conseguenza:
a=
m2
⋅g
m1 + m2
30
20
10
0
0
1
Fig. 4: Accelerazione in funzione del tempo
3B Scientific® Experiments
tn
m2
30
La causa di un’accelerazione costante è una forza costante F, se anche la
massa accelerata m non varia:
(3)
m1
...going one step further
2
t/s