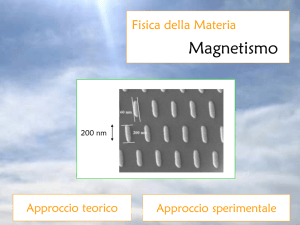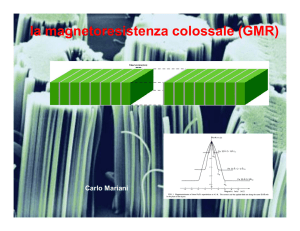
Molecole Magnetiche
Dante Gatteschi ([email protected])
&
Roberta Sessoli ([email protected])
Tel:055-457 3268
1
Chimica
Fisica
Magnetismo
molecolare
Biologia
/
Medicina
Scienza
dei Materiali
2
Mercato dei Magneti
Film per
registrazione
Calamite metaliche
(duri)
Ferriti duri
Particelle per
registrazione
Ferrite
Alta frequenza
(dolce)
Altre applicazione
Aciaio elettrico (dolce)
Materiali molecolari
3
Cenni Storici sul Magnetismo
800 a.c.: Le prime testimonianze scritte sul magnetismo
della magnetite (FeO-Fe2O3)
In Cina l’uso di un compasso
sembra risalire ad un periodo
molto anteriore (2000 a.c.)
L’origine del nome è incerta: dalla provincia greca dove
era stata trovata la roccia o dal nome del pastore le cui
scarpe chiodate furono attratte dalla roccia magnetizzata
(Plinio)
La prima individuazione dei poli magnetici risale al 1269
(Peregrinus)
Oersted e Ampere
• 1820 Oersted scopre che una corrente
elettrica influenza l’ago di una bussola
• Ampere suggerisce che correnti
elettriche interne sono responsabili del
ferromagnetismo e che queste correnti
fluiscono perpendicolari all’asse del
magnete. Le correnti devono essere
molecolari piuttosto che macroscopiche
5
La Meccanica Quantistica
• Hamiltoniano di scambio di Heisenberg,
Dirac, van Vleck
• Magnetismo come fenomeno cooperativo
• Antiferromagnetismo (Néel 1932)
• Teoria del ferromagnetismo (Slater 1937)
• Superscambio (Anderson 1951)
6
•Diamagnetismo
•Paramagnetismo
•Ferromagnetismo
•Antiferromagnetismo
ORDINE
A
LUNGO
RAGGIO
•Ferrimagnetismo
7
dimensionalità dello spin
Dimensionalità dello spin =3
modello di Heisenberg
Dimensionalità dello spin =2
modello XY o PLANARE
Dimensionalità dello spin =1
modello di Ising
8
dimensionalità del reticolo
(interazione magnetica)
3d
2d
1d
9
Ordine magnetico, dimensionalità dello
spin e dimensionalità del reticolo
Dimension. dello Spin
Dimensionalità del reticolo
2
1
1
NO
3
ORDINE
ORDINE
2
A LUNGO
A LUNGO
RAGGIO
3
per T≠
≠0
RAGGIO
T≠
≠0
10
Perchè studiare i materiali magnetici
Molecolari ?
• Nuovi fenomeni non
osservabili in magneti
tradizionali
• Sistemi modello
• Sistemi tunabili (‘magnets by
design’)
• Bassa densità
• Bio-compatibilità
• Trasparenza
November 2000
11
Un primo risultato
O
il primo (1991)
O
N
N
O
N
Tc= 0.6 K
O
F
S
F
N.
C
S N
F
N
Quello con Tc più
elevata
F
Tc=36 K
12
La Magnetizzazione dei Ferromagneti
Ms magnetizzazione di
saturazione
Mr magnetizzazione rimanente
Hc campo coercitivo
Hc→0 Magneti dolci (soft)
Hc ≠0 Magneti duri (hard)
13
Isteresi e struttura a domini
Per un ferromagnete l’energia si minimizza se si
formano domini: zone di spazio all’interno delle quali i
14
magneti elementari sono tutti paralleli tra di loro
L’anisotropia magnetica
• La magnetizzazione di un ferromagnete
tende a giacere lungo certi assi
cristallografici, detti assi facili
• L’energia di anisotropia è il lavoro che si
deve fare per orientare la
magnetizzazione lungo un certo asse
partendo dall’asse facile
15
Le pareti di Bloch
La parete è tanto più grande quanto più grande è l’interazione di
scambio e quanto è più piccola l’anisotropia.
Cosa succede quando le dimensioni del sistema sono
confrontabili con quelle di una parte di Bloch ?
16
Nanotecnologie
• Sistemi basati su
oggetti di dimensioni
di 100-102 nanometri
in almeno una
direzione
• Sviluppi resi possibili
dall’introduzione di
nuove tecniche tra
cui le microscopie a
scansione di sonda
AFM, STM, SPM
ecc.
17
Alcuni effetti importanti sono puramente legati
alle dimensioni
• Il rapporto atomi
superficiali/interni aumenta
al diminuire delle
dimensioni della particella
N
Est
Int
%int
1
2
3
4
..
8
1
6
12
18
...
42
0
1
7
19
...
127
0
14
37
51
..
75
superficiale
interno
18
There’s plenty of room at the
bottom
Un invito a entrare in un nuovo
campo della Fisica
19
Che cosa sono le nanotecnologie?
• Nanotecnologie vuol dire immaginare, progettare e
costruire strutture complesse con controllo su tutte le
scale, da quella atomica a quella macroscopica
• Le dimensioni nanometriche sono quelle giuste per
avere complessità sufficiente a introdurre proprietà
diverse
• Sviluppi rivoluzionari si possono attendere se si fa
molto lavoro di base
• Nell’attesa degli sviluppi rivoluzionari si può puntare a
sviluppi incrementali
20
Nobel per la Fisica 2007
Per la scoperta
della Magneto
Resistenza
Gigante, GMR
A: Fert, Orsay
P. Gruenberg,
Julich
21
Anisotropic magneto resistance
• “I found that iron, when subjected to a magnetic
force, acquires an increase of resistance to the
conduction of electricity along, and a diminution of
resistance to the conduction of electricity across, the
lines of magnetization”.
• W. Thomson, “On the Electro-Dynamic Qualities of
Metals: Effects of Magnetization on the Electric
Conductivity of Nickel and of Iron”, Proceedings of
the Royal Society of London, 8, pp. 546–550 (1856–
1857).
22
Magneto Resistenza, MR
• Gli elettroni hanno carica
elettrica e momento
magnetico (spin)
• In un conduttore magnetico lo
spin dell’elettrone può essere
parallelo o antiparallelo alla
magnetizzazione (effetto
quantistico)
• Gli elettroni con spin parallelo
alla magnetizzazione
vengono diffusi in modo
diverso dagli altri
• La variazione di R è
comunque al massimo di
qualche percento
23
Magneto Resistenza Gigante,
GMR
• Sistema a tre strati: 1 e 3
sono conduttori magnetici
(Fe), 2 è paramagnetico
(Cr, Cu)
• Magnetizzazione di 1
parallela a quella di 3
• Strati spessi alcuni nm
• Resistenza bassa
24
Magneto Resistenza Gigante,
GMR2
• Magnetizzazione di
3 antiparallela a
quella di 1
• Nessun elettrone si
muove bene
attraverso i tre strati:
• Resistenza alta
25
GMR per disco rigido
• 1988 la scoperta della
GMR
• 1996 IBM lancia le
testine a GMR
• Elevata sensibilità
consente di leggere
elementi di memoria
molto piccoli
26
Evoluzione della densità di immagazzinamento di
informazioni in supporti magnetici
27
MAGNETIZATION REVERSAL
macroscopic
permanent
magnets
S = 10
micron
particles
20
10
10
10
nanoscopic
nanoparticles
8
10
6
10
clusters
5
10
multi - domain
single - domain
nucleation, propagation and
annihilation of domain walls
uniform rotation
curling
1
4
molecular
clusters
3
10
10
2
Individual
spins
10
1
magnetic moment
quantum tunneling,
quantum interference
1
1
S
S
S
M/M
M/M
M/M
Fe8
0
0
0.7K
0
1K
-1
-40
-1
-20
0
20
µ 0H(mT)
40
0.1K
-1
-100
0
µ 0H(mT)
100
-1
0
µ 0H(T)
28
1
Il ruolo delle dimensioni nel processo di
inversione della magnetizzazione
Se l’inversione avviene attraverso la
suddivisione in domini l’energia in gioco nel
processo è ∝ R2 (n°di spin che non
minimizzano l’energia di scambio)
29
Il ruolo delle dimensioni nel processo di
inversione della magnetizzazione
Se l’inversione avviene attraverso la rotazione
coerente l’energia in gioco nel processo è ∝
all’anisotropia magnetica K x il numero di
spin coinvolti E∝
∝KV (E∝KR3 → il processo
collettivo è favorito per piccole dimensoni) 30
A bassa temperatura (T<<∆E/kB) diventa competitivo il
meccanismo di tunnel per l’inversione della
magnetizzazione
Energy
∆E=KV
θ
θ
31
Tunneling nella dinamica della
magnetizzazione
Prime evidenze in particelle di
dimensioni nanometriche
(problemi legati alle dimensioni non
omogenee)
0
3 nm
Ferridrite confinata all’interno
della ferritina (proteina
responsabile
dell’immagazzinamento del ferro
nei mammiferi)
(problemi legati al non omogeneo
carico di ferro)
32
Nano Magneti Molecolari
isteresi = memoria
in assenza di ordine a lungo raggio
Anche i sistemi 1d possono mostrare isteresi magnetica
Metallico
Molecolare
Caneschi et al.
P. Gambardella et al.
Nature 2002
Angew. Chem. 2001
1.8 K
3K
4K
5K
0.10
Mtotal (emu)
0.05
0.00
-0.05
-0.10
-40
-30
-20
-10
0
10
H (kOe)
20
30
40
34
[Mn12O12(CH3COO)16(H2O)4].2CH3COOH.4H20
Mn(III)
Mn(IV)
Oxygen
Carbon
S=10
35
Mn12ac: il primo magnete a singola
molecola (SMM)
τ= tempo caratteristico per l’inversione della magnetizzazione
25
τ=τ0exp(∆/kT)
-7
τ0=2x10 s;∆/k=62 K
log(τ)
15
1y
5
1h
1s
-5
2.5
5.0
T(K)
7.5
10.0
36
Mn12ac: il primo magnete a singola
molecola (SMM)
ciclo di isteresi
MAGNETIZATION (µB )
20
T=2.1K
10
0
-10
-20
-3
-2
-1
0
1
2
3
MAGNETIC FIELD (T)
37
Dalle nanoparticelle ai
magneti a singola molecola
• Il continuo di livelli
all’interno del doppio
pozzo si riduce a
livelli discreti e
diventano dominanti
gli effetti quantistici.
38
N
N S
S
S N
N
S
SN
S
N
SN
S
N
SN
S
N
N
N
S
S
S
N
S
N
N
Rilassamento della magnetizzazione: effetto classico
τ= τ0 exp(∆/kT)
N
N NN N S S S S S S
S
N
SSS
N NNN NN
S
S
Rilassamento della magnetizzazione: effetto quantistico
Magneti a Singola Molecola: una scuola di fisica
Programma I parte
• Introduzione
• Struttura elettronica degli ioni dei
metalli di transizione (6 ore):
–
–
–
–
ioni liberi e legati
repulsione elettronica
accoppiamento spin orbita
campo dei leganti e cenni di
simmetria (teoria dei gruppi)
• Hamiltoniano di spin (4 ore):
–
–
–
–
Formalismo
termini di Zeeman
zero field splitting
interazione spin elettronico spin
nucleare
• Spettroscopia di Risonanza
Paramagnetica Elettronica
Struttura elettronica degli ioni dei
metalli di transizione (2-4 ore):
– Principi
– Determinazione dei parametri del
Hamiltoniano di spin
– Strumentazione ed esercitazione
di registrazione e lettura di spettri
EPR
41
• Interazione spin spin (4 ore)
– hamiltoniano di spin per coppie
– relazioni tra parametri dell’
hamiltoniano di spin
• Operatori tensoriali irriducibili (2
ore)
• Hamiltoniano di spin per n ioni (2
ore)
• Tecniche di caratterizzazione
delle proprietà magnetiche (4
ore):
–
–
–
–
Metodi di forza
Metodi induttivi
Misure di momento torcente
Strumentazioni ed esercitazioni
• Modelli orbitali dell’interazione di
scambio (2 ore)
42
Magnetic quantities & units / 1
magnetic moment
Quantity name
alias magnetic dipole moment
or electromagnetic moment
Quantity symbol
m
ampere metre squared (or J/T)
emu (or erg/G)
A m2
Unit name
Unit symbols
τ = B × m × sinθ
Quantity symbol
Magnetic flux density,
alias Magnetic induction
B
Unit name
Tesla - gauss
Unit symbol
T -G
Quantity name
kg
Base units
s-2
B = µ0 ( H + M)
A-1
43
Magnetic quantities & units / 2
Quantity name
magnetic field strength
alias magnetic field intensity
Quantity symbol
H
Unit name
Ampere per metre / Oe
Unit symbols
A m-1 / Oe
So it seems that H describes the way magnetism is generated by moving electric
charge (which is what a current is), while B is to do with the ability to be detected
44 by
moving charges.
(Volume) Magnetization is defined as
The sum of the magnetic moments
in the unit of volume
M = m / V (A m-1 o emu/cm3 )
(Volume) Susceptibility is defined as:
χ = ∂M/ ∂H = dimensionless ( o emu/cm3 )
Permeability is defined as:
µ = B/H = (H m-1 o dimensionless)
Conversion Table
Magnetization and Susceptibility can be expressed as unit per mass
and therefore the above units are multiplied by m3kg-1 (cm3g-1) or
45
per mole and the units are multiplied by m3mol-1 (cm3mol-1)
Magnetic Term
Symbol
SI unit
CGS unit
conversion factor
magnetic
induction
B
Tesla (T)
Gauss (G)
1 T = 104 G
magnetic field
H
A/m
Oersted (Oe)
1 A/m =4p/103 Oe
magnetization
M
A/m
emu/cm3
1 A/m = 10-3 emu/cm3
mass
magnetization
s
Am2/kg
emu/g
1 Am2/kg = 1 emu/g
magnetic
moment
m
Am2
emu
1 Am2 = 103emu
volume
susceptibility
k
dimensionless
dimensionless
4π (SI) = 1 (cgs)
mass
susceptibility
c
m3/kg
emu/Oe·g
1 m3/kg = 103/4π emu
/Oe·g
permeability of
free space
µ0
H/m
dimensionless
4πx10-7 H/m = 1 (cgs)
A= Ampere
cm= centimeter
emu= electromagnetic unit
g= gram
kg= kilogram
m= meter
H= Henry
46
47
48
momenti angolari
In meccanica classica si definisce il momento angolare come
Proprietà di commutazione degli operatori quantistici
Inoltre, dati due vettori e (sempre corrispondenti ad operatori quantistici),
si può costruire l'operatore ``prodotto scalare''
Con le proprietà
di commutazione:
ed in particolare:
49
Momenti angolari
Da un punto di vista formale si può definire momento angolare un operatore
vettoriale che sia hermitiano e che soddisfi l'algebra di commutazione
[ J x , J y ] = iℏJ z
[ J y , J z ] = iℏJ x
[ J z , J x ] = iℏJ y
Che garantisce:
E’ importante ricordare come operano gli operatori momento angolare:
J z J , M = ℏm J , M
Dove –j ≤ m
J 2 J , M = ℏ 2 ( j ( j + 1)) J , M
J + J , M = ℏ j ( j + 1) − m(m + 1) J , M + 1
≤ j per intervalli interi
J − J , M = ℏ j ( j + 1) − m( m − 1) J , M − 1
dove:
J + = J x + iJ y
J − = J x − iJ y
1
(J+ + J− )
2
i
J y = − (J+ − J− )
2
Jx =
50
Composizione di Momenti Angolari
Questo porta a un numero di stati =
Definiamo un nuovo operatore somma
con
(2 j1 + 1)(2 j2 + 1)
J = J1 + J 2
| J 1 − J 2 |≤ J ≤ J 1 + J 2
Se c’è accoppiamento
e per ogni J
−J ≤ M J ≤ +J
H = kJ 1 ⋅ J 2
Per calcolare gli elementi di matrice dell’interazione possiamo sfruttare:
J 2 = ( J 1 + J 2 ) 2 = J 12 + J 2 2 + 2 J 1 ⋅ J 2
,
J1 ⋅ J 2 =
Ricordiamo che questa volta è
1 2
( J − J 12 + J 2 2 )
2
J z = ( J 1, z + J 2, z )
ad essere conservato e non le singole componenti
51