II Prova in Itinere di Fisica IB – 24 giugno 2008 – Ore 14 –

II Prova in Itinere di Fisica IB – 24 giugno 2008 – Ore 14 –
Indicare sul proprio elaborato NOME e COGNOME e NUMERO DI MATRICOLA
1) la prova è valida se affrontata individualmente; ogni tipo di comunicazione, verificata durante o dopo la prova, comporta
l’invalidazione della stessa. Un telefono cellulare acceso comporta l’annullamento della prova
2) la prova va affrontata senza alcun ausilio di libri di testo e/o appunti; sul banco devono trovare posto solo testo della
prova ed i fogli forniti, penna e calcolatrice numerica; zaini e borse devono essere depositati lungo i corridoi laterali.
3) nella soluzione dei problemi, sempre fornire prima il procedimento ed il risultato simbolico e successivamente il risultato
numerico; il testo deve essere scritto a penna e in forma leggibile; non verranno considerate soluzioni che risultano ambigue
a causa di disordine o scrittura poco leggibile del candidato.
4) ad ogni esercizio è accreditato di un punteggio in 30esimi; la media dei punteggi ottenuti nelle due prove in itinere (se
superiore a 18) sarà il voto di ammissione all’esame orale. L’esame orale si terrà a luglio e includerà la discussione della
prova scritta e domande di carattere teorico sul corso; la discussione sarà più approfondita nelle situazioni di limite per
assestare la sufficienza o l’eccellenza e nei casi di dubbia paternità della prova. Il voto finale tiene conto del punteggio delle
prove scritte e dell’orale.
Le soluzioni e l’esito della prova saranno pubblicati anche sul sito http://www.unipv.it/fis/fisica1B.
B
Esercizio 1: Un tubo di sezione costante viene usato per rimuovere dell'acqua da un
recipiente che non può essere capovolto come mostrato in figura. Sapendo che h1=1 m ,
h2=80 cm e che all'inizio h=h0=30 cm, che l'area della base del recipiente è Σ=2 m2 e che
il raggio del tubo è r=1 cm, si calcoli:
a) la velocità iniziale di fuoriuscita del liquido in C;
b) la pressione iniziale del liquido nel punto più alto B;
c) il tempo necessario perché il livello dell'acqua nel recipiente arrivi all'entrata del tubo
in A. (9 punti)
h1
h
A
h2
C
Esercizio 2: Un tubo alto L=25 m ha l'estremità superiore chiusa, quella
inferiore aperta e contiene aria inizialmente a pressione atmosferica. Il tubo
viene spinto verticalmente nell'acqua di un lago fino a che l'acqua non
riempie il tubo fino a metà altezza (come in figura). Qual'è la profondità h
dell'estremità aperta del tubo? Si consideri l'aria un gas perfetto; le
temperature iniziali e finali sono uguali. (5 punti)
L/2
L/2
h
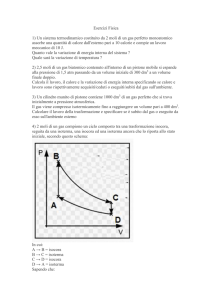
Esercizio 3: Due moli di gas ideale monoatomico sono contenute in un recipiente alla temperatura TA = 300K.
Al fine di dimezzare pressione e volume iniziali PA, VA, il gas viene sottoposto a due trasformazioni
consecutive: una compressione isoterma reversibile AB, che ne dimezza il volume; una isocora irreversibile
BC, realizzata ponendo il gas a contatto con una sorgente a temperatura TC, che ne porta la pressione a
1
P C = P A . Calcolare le quantità di calore scambiate con le sorgenti e la variazione di entropia
2
dell'universo. (5 punti)
Esercizio 4: In un giorno d'estate la temperatura è di 35 °C mentre l'acqua di un pozzo profondo 20 m è alla
temperatura di 15 °C. Mediante una macchina che operi fra queste due sorgenti si vogliono prelevare 50 l di
acqua dal pozzo.
a) Calcolare la minima quantità di calore che la macchina deve cedere all'acqua del pozzo.
b) Se la macchina ha un rendimento del 30% di quello di una macchina reversibile, calcolare la variazione di
entropia dell'universo e il lavoro sprecato durante il processo. (8 punti)
Esercizio 5:
Una mole di gas ideale monoatomico compie un ciclo costituito da un'espansione adiabatica da TA=600 K a
TB=300 K, una compressione isoterma fino al volume iniziale VA ed una trasformazione isocora fino a che la
temperatura ritorna al valore TA. Calcolare il rendimento e il lavoro fornito dalla macchina in un ciclo. (6
punti)
Soluzioni:
Esercizio 1:
a)
1
m
 g  h2h0  p atm =  v C2  p atm ⇒ v C = 2 g  h 0h 2 =4.65
2
s
b) la sezione del tubo è costante, quindi la velocità dell'acqua in tutti i punti del tubo è uguale alla velocità di
1
2
2
uscita, quindi P B  g h 1  v C = patm ⇒ P B= p atm− g  h0h2h1 =0.8 atm=80700 Pa
c)
dV
=r 2 v= r 2  2 g  hh2  e
dt
T=
h0h2

r
2
 2g
∫
h2
dy

= 2
 y r

dV
dh
=
quindi
dt
dt
h0
T
dh
=∫ dt
∫ hh
2
 r 2 g 0 
2
0

2
 h h − h =443.8 s
g  0 2  2
Esercizio 2:
[
 ]
detta S la sezione del cilindro p atm S L= p atm  g h−
Esercizio 3:
Nell'isoterma
Nell'isocora
L
2
S
p
L
L
⇒ h= atm  =22.83 m
2
g 2
VB
=−3458 J : il calore viene ceduto. P B V B =P A V A ⇒ P B =2 P A
VA
T A TC
T
3
Q BC =n RT C −T A =−5612 J : il calore viene ceduto.
=
⇒T C = A
2
PB PC
4
Q AB=n RT A ln
La prima trasformazione è reversibile, quindi la variazione dell'entropia dell'universo è nulla. Per la seconda
 S u= S gas  S T =nc V ln
C
Esercizio 4:
il lavoro che si deve compiere è
dell'acqua che si vuole estrarre.
T C Q BC
J
−
=40.26
T A TC
K
W =Mgh=9810 J , dove h è la profondità del pozzo e
 1 
QC =W −Q A=W 1−
a) il calore ceduto dalla macchina è
Q Ap=−QC =W
 1 −1
e quello assorbito dall'acqua del pozzo è
che è tanto più piccolo quanto più è grande

M la massa
 , cioè nel caso di ciclo reversibile

T1
1
p , min
−1 =141.2 kJ
=0.065 . Quindi Q A =W
R
T2
−Q A Q C
1
1
1
W
J
− =W −
− 
=
R −=79.5
b) nel caso =0.3⋅ R si ha  S U =
,e
T2
T1
 T 2 T 1 T 1  T 1
K
il lavoro sprecato è W S =T 1⋅ S U =22.9 kJ (se si considera anche la variazione di entropia della massa di
T2
J
=14052
acqua estratta che si scalda si deve aggiungere  S A=M c A ln
alla variazione di entropia
T1
K
 R=1−


dell'universo, ma tale variazione di entropia non corrisponde ad un passaggio di calore dalla sorgente calda a
quella fredda, quindi non deve comparire nel calcolo del lavoro sprecato)
Esercizio 5:
 
1
V
T −1
T A V =T B V ⇒ A = B
VB
TA
V
RTB T B
3
Q BC =R T B ln A =
ln =−2594 J , Q CA = R  T A−T A =3742 J
2
V B −1 T A
W
=0.307
W =Q BC Q CA=1148 J , =
Q CA
−1
A
−1
B