Panoramica di Teoria dei Modelli
Antongiulio Fornasiero & Tamara Servi
27 agosto 2015
Introduzione
Questo mini-corso è rivolto ad un pubblico misto di filosofi, informatici e
matematici, di livello e preparazione molto diversi. La Scuola Estiva di Logica
di Gargnano ha già ospitato diverse volte ottimi corsi istituzionali di teoria dei
modelli. Per cambiare un po’, abbiamo deciso quest’anno di offrire un corso un
po’ meno classico, con le seguenti proprietà: non potendo presupporre molti
prerequisiti, cercheremo di partire dai concetti di base. Tuttavia, volendo
arrivare a coprire del materiale piuttosto avanzato in poco tempo, alcuni
concetti e definizioni saranno spiegati in modo informale e discorsivo, facendo
appello all’intuizione e ad esempi concreti.
Lo scopo di questo corso è di dare una panoramica su alcuni temi fondamentali
della teoria dei modelli e sui problemi matematici che motivano ed
esemplificano le definizioni e i risultati che presenteremo. L’enfasi sarà sui temi
dell’eliminazione dei quantificatori, della model-completezza e della decidibilità
per strutture aventi come dominio R o C.
Prerequisiti/organizzazione
Assumeremo che lo studente conosca, oltre ai primi rudimenti della logica del
prim’ordine, le proprietà fondamentali dell’insieme dei numeri naturali N,
dell’insieme dei numeri interi Z, dell’insieme dei numeri razionali Q, dell’insieme
dei numeri reali R e dell’insieme dei numeri complessi C.
Alcuni esempi ed esercizi (notati con un asterisco) richiederanno delle nozioni
di algebra, topologia e analisi non del tutto elementari (funzioni continue,
derivabili, analitiche; caratteristica di un campo, chiusura algebrica;...).
In questo corso, tutto si svolge all’interno della logica del prim’ordine.
La Teoria dei Modelli può essere vista come lo studio della relazione tra le
formule e le strutture che le soddisfano (o refutano).
Cominceremo dunque il nostro corso fissando una notazione per questi concetti
di base.
1. Strutture e formule
Definizione 1.1 (Struttura) Sia dato un linguaggio L (ovvero, un insieme di
simboli delle seguenti tipologie: costante, relazione, funzione).
Una L-struttura A è il dato di un insieme non vuoto A (detto dominio) e di una
funzione di interpretazione che:
- ad ogni simbolo di costante di L associa un elemento di A;
- ad ogni simbolo di relazione n-ario di L associa un sottoinsieme di An ;
- ad ogni simbolo di funzione n-ario di L associa una funzione da An in A.
Esempi. 1.2
Dato il linguaggio L = {0, 1, +, ·}, la L-struttura A = hZ; 0, 1, +, ·i ha come
dominio l’insieme dei numeri interi e i simboli di L sono interpretati nella
maniera solita.
Dato il linguaggio L0 = {≤}, la L0 -struttura B = hZ; ≤i ha sempre l’insieme
dei numeri interi come dominio, ma questa volta il linguaggio contiene solo un
simbolo di relazione binaria, che interpretiamo come la relazione d’ordine
usuale.
Osservazioni 1.3
1. La notazione A = hZ; 0, 1, +, ·i richiama il fatto che vogliamo interpretare i
simboli di L nel modo solito. Questa notazione abbrevia la seguente notazione
più formale:
D
E
A = Z; 0A , 1A , +A , ·A ,
dove si specifica esplicitamente che l’interpretazione 0A del simbolo di costante
0 ∈ L è l’elemento zero dell’insieme dei numeri interi, l’interpretazione +A del
simbolo di funzione binaria + ∈ L è la somma usuale di numeri interi, ecc.
Quando possibile, si scelgono i simboli del linguaggio avendo già in mente
un’interpretazione (standard, comunemente accettata e conosciuta).
2. Consideriamo il linguaggio L00 = L ∪ L0 ottenuto espandendo il linguaggio L
con il simbolo di relazione ≤. La L00 -struttura C = hZ; 0, 1, +, ·, ≤i (che si
ottiene interpretando come al solito i simboli di L00 ) si dice un’espansione sia di
A che di B, e viceversa diciamo che A e B sono restrizioni di C. È evidente
che, rispetto alle altre due strutture, C è più ricca (possiamo parlare di più
proprietà di Z).
Per formalizzare questa idea, ci serve il concetto di formula.
Formule
Definizione 1.4 Sia dato un linguaggio L.
Una L-formula è un’espressione formale costruita a partire da un insieme di
variabili, usando le parentesi (, ), i connettivi logici ∨, ∧, ¬, →, i quantificatori
∃, ∀, i simboli di L ∪ {=}, nel modo seguente:
• dapprima costruiamo gli L-termini: un termine è una variabile, oppure un
simbolo di costante di L, oppure un’espressione f (t1 , . . . , tn ) dove ti sono
termini precedentemente costruiti e f è un simbolo di funzione n-ario di L;
• poi costruiamo le formule atomiche, ovvero le espressioni t1 = t2 (dove ti
sono L-termini) oppure le espressioni R (t1 , . . . , tn ) (dove R è un simbolo di
relazione n-ario di L e ti sono L-termini);
• infine, l’insieme delle L-formule è definito induttivamente come segue:
- ogni formula atomica è una formula;
- se α, β sono formule costruite precedentemente, allora
(α ∧ β) , (α ∨ β) , (¬α) , (α → β) sono formule;
- se α è una formula costruita precedentemente e x è una variabile,
allora ∃x α, ∀x α sono formule;
- nient’altro è una formula.
Esempi 1.5
Dato il linguaggio L = {0, 1, +, ·}, le espressioni seguenti sono L-formule:
x = y ; ∀x (x + y = x + 0) ; ∃x (x · x = x) ; x = 0 → x + x = y .
Una L-formula è un’espressione formale. Una L-struttura è il dato di un insieme
e di una funzione di interpretazione. Per mettere in relazione questi due
concetti, bisogna chiarire come si interpreta una L-formula in una L-struttura.
Informalmente, data una L-formula ϕ e una L-struttura A, se assegnamo ad
ogni variabile non quantificata di ϕ un elemento del dominio di A, e
interpretiamo i simboli di L usando la funzione di interpretazione di A
(l’interpretazione dei simboli logici è fissa), otteniamo un’interpretazione di ϕ in
A, ovvero un’affermazione (che può essere vera o falsa) sul comportamento
degli elementi del dominio di A rispetto alle funzioni e relazioni di A.
Esempi 1.6
Sia A = hZ; 0, 1, +, ·i. Data la formula x = y , se assegnamo a x il numero
intero 1 e a y il numero intero 2, allora la formula interpretata “1=2” è
un’affermazione (falsa) nella struttura A.
Se invece assegnamo a x e y lo stesso numero intero, l’affermazione diventa
vera. La formula ∃x (x · x = x) ha un’unica interpretazione in A, in quanto
tutte le variabili che vi appaiono sono quantificate e non c’è una scelta da fare.
Ha dunque senso chiedersi se questa formula sia vera o falsa in A
(indipendentemente dalla valutazione delle variabili).
Definizione 1.7 (Enunciato) Una formula senza variabili libere (ovvero, in cui
compaiono solo variabili quantificate) si dice enunciato.
Data una L-struttura A e un L-enunciato ϕ, se ϕ è vera in A scriviamo
A |= ϕ.
Notiamo che, per ogni enunciato ϕ, si ha che A |= ϕ o A |= ¬ϕ.
Esempio 1.8
Sia L = {e, ⊕, }, dove e è un simbolo di costante, ⊕ è un simbolo di funzione
binaria e è un simbolo di funzione unaria. Una L-struttura G è un gruppo se
i seguenti enunciati sono veri in G:
• (associatività) ∀x, y , z ((x ⊕ y ) ⊕ z = x ⊕ (y ⊕ z)).
• (elemento neutro) ∀x (e ⊕ x = x ∧ x ⊕ e = x).
• (inverso) ∀x ((x) ⊕ x = e ∧ x ⊕ (x) = e).
Esercizi.
Tradurre le seguenti affermazioni in un linguaggio appropriato come enunciati
veri nelle relative opportune strutture.
1. Z è un anello, ovvero un gruppo abeliano rispetto alla somma, un monoide
rispetto alla moltiplicazione e la moltiplicazione è distributiva rispetto alla
somma.
2. Q è un campo, ovvero un anello dove ogni elemento diverso da zero ha un
inverso moltiplicativo.
3. R è un campo ordinato, ovvero un campo dotato di una relazione d’ordine
totale compatibile con somma e prodotto.
4. C è un campo algebricamente chiuso, ovvero ogni polinomio in una
variabile e a coefficienti in C ha una radice in C.
Osservazione 1.9 Una formula può esser scritta, grazie a manipolazioni
elementari, nella seguente forma normale
Q1 x1 . . . Qn xn α (x1 , . . . , xn , y1 , . . . , ym ) ,
dove α è una formula senza quantificatori con le variabili x1 , . . . , xn , y1 , . . . , ym
come variabili libere e Qi ∈ {∃, ∀}.
Possiamo inoltre supporre che α sia una disgiunzione finita di congiunzioni
finite di formule atomiche e negazioni di formule atomiche.
Notazione 1.10 La notazione ϕ (y1 , . . . , ym ) significa che le variabili libere di ϕ
appartengono all’insieme {y1 , . . . , ym }. Non si notano invece esplicitamente le
variabili quantificate, in quanto si tratta di variabili “mute” o “segna-posto”.
Sia A una L-struttura e sia A il dominio di A. Se (a1 , . . . , am ) ∈ Am ,
l’espressione A |= ϕ (a1 , . . . , am ) significa che l’interpretazione di ϕ in A nella
quale si assegna il valore ai alla variabile yi , è vera in A.
2. Insiemi definibili
Date una formula ϕ (y ), dove y = (y1 , . . . , ym ), e una struttura A, è naturale
chiedersi per quali scelte di a = (a1 , . . . , am ) ∈ Am si ha che A |= ϕ (a).
Definizione 2.1 (Insiemi ∅-definibili) Sia A una L-struttura, n ∈ N e D ⊆ An un
sottoinsieme. Si dice che D è ∅-definibile in A se esiste una L-formula
ϕ (y1 , . . . , yn ) tale che
D = {a ∈ An : A |= ϕ (a)} .
Una parte della teoria dei modelli è dedicata allo studio degli insiemi definibili
in una certa struttura: qual è la loro natura? È possibile descriverli in modo
“semplice”? Come stabilire se un dato insieme è o meno definibile in una data
struttura?
Esempio 2.2 Consideriamo l’insieme dei numeri complessi con la struttura di
campo C = hC; 0, 1, +, −, ·i.
• L’insieme {a ∈ C : a · a + a · a + a · a − a − a + 1 = 0} è ∅-definibile. Più in
generale, i termini del linguaggio di C sono tutti e soli i polinomi a coefficienti
in Z; dunque l’insieme delle soluzioni di un’equazione polinomiale a coefficienti
in Z è ∅-definibile.
• L’insieme delle soluzioni di un’equazione polinomiale a coefficienti in Q è
∅-definibile (esercizio).
• L’insieme
(a, b, c) ∈ C3 : (a 6= 0 ∨ b 6= 0) ∧ ∀x ax 2 + bx + c 6= 0
è ∅-definibile(è l’insieme vuoto!).
• L’insieme (a, b) ∈ C2 : a2 − 3a + 1 = b è ∅-definibile. Si tratta del grafico
2
della funzione polinomiale p (z) = z − 3z + 1.
Definizione
funzione f : Am→ A si dice ∅-definibile se il suo grafico
2.3 Unam+1
Γ (f ) = (x, y ) ∈ A
: f (x) = y è un insieme ∅-definibile.
Esempio 2.4 Tutte le funzioni polinomiali a coefficienti in Q sono ∅-definibili in
C. Cosa possiamo dire delle funzioni polinomiali a coefficienti in C?
Definizione 2.5 (Insiemi definibili con parametri) Sia A una L-struttura, n ∈ N
e D ⊆ An un sottoinsieme. Si dice che D è definibile con parametri in A se
esistono un’espansione L0 di L, ottenuta aggiungendo dei simboli di costante, e
una L0 -formula ϕ (y1 , . . . , yn ) tale che
D = {a ∈ An : A |= ϕ (a)} .
In altre parole, ϕ è della forma ψ (c1 , . . . , cm , y1 , . . . , yn ), dove ci sono nuovi
simboli di costante e ψ (x, y ) è una L-formula con m + n variabili libere.
L’insieme dei parametri è l’insieme delle interpretazioni di c1 , . . . , cm .
Dato A0 ⊆ A, diciamo che D è A0 -definibile se D è definible con parametri
appartenenti all’insieme A0 . Di conseguenza, gli insiemi ∅-definibili sono gli
insiemi definibili senza parametri.
Un insieme definibile con parametri non è dunque altro che un insieme
∅-definibile nell’espansione A0 di A che si ottiene aggiungendo a L un simbolo
di costante per ogni elemento di A (e intepretandolo come l’elemento in
questione).
Analogamente, si definisce il concetto di funzione definibile con parametri.
Notazione 2.6 D’ora in poi useremo l’espressione “definibile” per un insieme
definibile con parametri.
Esempio 2.7
L’insieme delle soluzioni di un sistema di equazioni polinomiali a coefficienti in
C è definibile in C.
L’insieme
Calg = {a ∈ C : ∃ un polinomio p (z) ∈ Z [z] t.c. p (a) = 0} ,
come sottoinsieme di C, non è invece definibile (lo vedremo in seguito).
Esercizio. Ogni sottoinsieme finito del dominio di una struttura è definibile con
parametri. Lo stesso vale per ogni sottoinsieme co-finito.
Osservazioni 2.8
• Dato A0 ⊆ A, la collezione Defn (A, A0 ) dei sottoinsiemi di An che sono
A0 -definibili forma una sottoalgebra di Boole dell’algebra di Boole di tutti i
sottoinsiemi di An . In altre parole, Defn (A, A0 ) è chiusa rispetto alle operazioni
insiemistiche di intersezione, unione e complementare. Questo segue dal fatto
che la congiunzione, la disgiunzione, la negazione di formule è ancora una
formula.
[
• La collezione
Defn (A, A0 ) è chiusa per proiezione nel senso seguente:
n∈N
sia D ∈ Defn (A, A0 ) e sia π : An → Ai la proiezione sulle prime i coordinate
(per un qualche i ≤ n). Allora π (D) ∈ Defi (A, A0 ). Infatti, se ϕ (x1 , . . . , xn ) è
una formula che definisce D, la formula ∃xi +1 . . . ∃xn ϕ definisce π (D).
Osservazione 2.9 Sia D ⊆ An un insieme definibile. È evidente che esistono
infiniti modi di definire D, ovvero infinite formule che possono essere usate per
la definizione di D (se ϕ è una tale formula e θ è una qualunque tautologia,
allora anche ϕ ∧ θ è una formula che definisce D). Uno degli scopi della teoria
dei modelli è quello di trovare formule “semplici” per definire gli insiemi.
Associamo (in modo un po’ informale) ad ogni formula in forma normale una
nozione di complessità.
Essenzialmente, consideriamo le formule senza quantificatori come le più
semplici;
le formule in cui tutti i quantificatori sono dello stesso tipo (formule esistenziali
e formule universali) sono le formule più semplici in cui compaiano dei
quantificatori;
procedendo così, maggiore è l’alternanza tra quantificatori esistenziali e
universali, maggiore è la complessità.
Questa nozione di “semplicità” e “complessità” riflette il fatto che, dato un
insieme definibile D ⊆ An e una n-upla a ∈ An , verificare se a appartiene a D o
meno è tanto più difficile quanto più la formula che definisce D è complessa.
Ritorneremo su questo punto più tardi.
Esempio 2.10
Consideriamo l’insieme dei numeri reali con la struttura di campo ordinato
R = hR; 0, 1, +, −, ·, <i.
Gli insiemi definibili senza quantificatori in questa struttura si chiamano insiemi
semialgebrici.
Si tratta di combinazioni booleane di insiemi della forma {a ∈ Rn : p (a) = 0}
e della forma {a ∈ Rn : p (a) < 0} (dove n ∈ N e p (x) ∈ R [x]).
Osserviamo che, se p, q ∈ R [x] e a ∈ Rn , allora
p (a) · q (a) = 0 ⇔ p (a) = 0 ∨ q (a) = 0 e
p (a)2 + q (a)2 = 0 ⇔ p (a) = 0 ∧ q (a) = 0.
Inoltre, p (a) 6= 0 ⇔ p (a) < 0 ∨ −p (a) < 0.
Grazie a queste osservazioni e a facili manipolazioni, si può dimostrare
(esercizio) che ogni insieme semialgebrico si può scrivere come unione finita di
insiemi della forma
{a ∈ Rn : p (a) = 0, q1 (a) < 0, . . . , qr (a) < 0} .
Dunque gli insiemi definibili senza quantificatori hanno una forma piuttosto
semplice, se scegliamo la formula definente in modo intelligente.
Vediamo ora un esempio di insieme definibile in R con quantificatori.
Consideriamo l’insieme dei coefficienti a, b, c ∈ R tali che l’equazione di
secondo grado ax 2 + bx + c = 0 ha soluzione in R, ovvero l’insieme
(a, b, c) ∈ R3 : ∃x ax 2 + bx + c = 0 .
Lo stesso insieme può essere definito da una formula più semplice, senza
quantificatori:
(a, b, c) ∈ R3 : a 6= 0 ∧ 4ac − b 2 ≤ 0 ∨ (a = 0 ∧ (b 6= 0 ∨ c = 0)) .
Cosa succede se consideriamo un insieme definito da una formula più
complessa, con un alternanza di quantificatori?
Un teorema di Tarski molto profondo che vedremo in seguito ci dice che tutti
gli insiemi definibili sono definibili con una formula senza quantificatori.
In altre parole, tutti gli insiemi definibili sono semialgebrici.
Osservazione.
La relazione d’ordine “<” è definibile a partire dalla somma e dal prodotto,
sfruttando il fatto che i numeri reali strettamente positivi sono tutti e soli i
quadrati non nulli:
a < 0 ⇔ ∃x −a · x 2 = 1 .
Tuttavia, questa definizione introduce un quantificatore.
Per questo motivo conviene considerare la relazione d’ordine come primitiva
(ovvero includerla nel linguaggio).
Esercizio. Descrivere i sottoinsiemi di R definibili in R senza quantificatori.
Esercizio. (*) Si consideri la topologia euclidea su R, e siano f : R → R e
D ⊆ Rn rispettivamente una funzione e un insieme definibili in R.
Scrivere un enunciato che afferma che f è una funzione continua e che D è un
insieme aperto (rispetto alla topologia euclidea).
Esempio 2.11 Consideriamo il linguaggio L = {+, ·} e le due L-strutture N e Z,
di dominio N e Z rispettivamente, dove i simboli di L sono interpretati come la
somma e il prodotto usuali. L’insieme N, visto come il sottoinsieme di Z
composto dai numeri non negativi, può essere definito in Z senza parametri,
grazie a un teorema di Lagrange che afferma che:
a ∈ N ⇔ ∃x, y , z, t a = x 2 + y 2 + z 2 + t 2 .
Poiché la somma e il prodotto di numeri naturali non sono altro che le
restrizioni a N della somma e prodotto di numeri interi, possiamo dire che
l’intera struttura N è “∅-definibile” in Z. Il teorema di Gödel afferma che la
struttura N non è decidibile, nel senso che non esiste un algoritmo che decida,
dato un L-enunciato ϕ, se ϕ sia vero o falso in N. D’altro canto, l’osservazione
precedente ci fornisce (esercizio) un metodo esplicito (algoritmico) per tradurre
ogni L-enunciato ϕ in un L-enunciato ϕ0 tale che
N |= ϕ ⇔ Z |= ϕ0 .
Ne deduciamo che anche la struttura Z non è decidibile. Questo esempio
mostra che la definibilità gioca un ruolo importante anche in relazione a
problemi di decidibilità (vedremo più dettagli su questo tema in seguito).
3. Teorie e modelli
Dato un linguaggio L, un L-enunciato ϕ e due L-strutture A e B, naturalmente
è possibile che A e B siano d’accordo o siano in disaccordo sulla verità di ϕ.
Esempi 3.1
Le strutture Q = hQ; 0, 1, +, −, ·, <i e R = hR; 0, 1, +, −, ·, <i sono entrambe
campi ordinati, e dunque concordano sul valore di verità degli assiomi di campo
ordinato.
Tuttavia, se ϕ è l’enunciato ∃x x 2 = 2 , abbiamo che Q |= ¬ϕ e R |= ϕ.
Le strutture hZ; 0, 1, +, ·i e hZ/2Z; 0, 1, +, ·i, pur essendo entrambe anelli,
non concordano sul valore di verità dell’enunciato 1 + 1 = 0.
Definizione 3.2 Dato un linguaggio L, due L-strutture A, B si dicono
elementarmente equivalenti (e si scrive A ≡ B) se soddisfano esattamente gli
stessi L-enunciati, ovvero:
∀ϕ L-enunciato, A |= ϕ ⇔ B |= ϕ.
Una domanda naturale si pone: date A, B, come stabilire se esse sono
elementarmente equivalenti o meno? E ancora: data A, come caratterizzare
tutte le L-strutture ad essa elementarmente equivalenti?
Definizione 3.3 Sia dato un linguaggio L.
• Una L-teoria T è un insieme di L-enunciati (che vengono anche chiamati
assiomi).
• Data una L-teoria T , una L-struttura A è un modello di T se
∀ϕ ∈ T , A |= ϕ.
Denotiamo con Mod (T ) la classe di tutti i modelli di T .
• Data una L-teoria T e un L-enunciato ϕ, si dice che ϕ è conseguenza logica
di T (e si scrive T |= ϕ) se ϕ è vera in ogni modello di T .
• Data una L-teoria T , definiamo la chiusura deduttiva T di T come l’insieme
degli enunciati che sono conseguenza logica di T .
Si osservi che Mod (T ) = Mod T .
• Una L-teoria T è completa se per ogni L-enunciato ϕ si ha che T |= ϕ
oppure T |= ¬ϕ.
Data una L-struttura A, denotiamo con Th (A) la teoria completa di A, ovvero
l’insieme di tutti gli L-enunciati che sono veri in A (si tratta di una teoria
completa e deduttivamente chiusa (esercizio)).
Per semplicità, in questo corso considereremo solo teorie che abbiano almeno
un modello (ovvero teorie coerenti ).
Esempio 3.4 La collezione degli assiomi di campo forma una teoria.
Non si tratta di una teoria completa, poiché esistono enunciati che sono veri in
alcuni modelli ma falsi in altri (vedi Esempio 3.1).
Lemma 3.5 Sia T una L-teoria. Le seguenti affermazioni sono equivalenti:
1.
2.
3.
4.
∀A, B ∈ Mod (T ) si ha A ≡ B.
T è completa.
Se T 0 ⊇ T è una L-teoria, allora T 0 = T .
T = Th (A) per un qualunque A ∈ Mod (T ).
Dimostrazione. Assumiamo 1. e sia ϕ un L-enunciato. Supponiamo che ϕ non
sia conseguenza logica di T . Questo vuol dire che esiste un modello A di T in
cui è vera ¬ϕ. Per 1., ¬ϕ è vera in tutti i modelli di T , ovvero T |= ¬ϕ.
Assumiamo 2. e sia ϕ ∈ T 0 . Poiché T è completa, si ha che o ϕ ∈ T oppure
¬ϕ ∈ T . Ma se ¬ϕ ∈ T ⊆ T 0 , avremmo che T 0 sarebbe incoerente, quindi
necessariamente ϕ ∈ T .
Assumiamo 3. e sia A un modello di T . È evidente che T ⊆ Th (A). Grazie a
3., concludiamo che T = Th (A).
Infine, assumiamo 4. ∀A, B ∈ Mod (T ) si ha Th (A) = Th (B), e dunque
A ≡ B.
Dunque, data una classe di L-strutture, se esiste una teoria completa di cui
tutte le strutture della classe siano modello, allora tutte le strutture della classe
sono elementarmente equivalenti.
4. Assiomatizzazioni e decidibilità
Definizione 4.1 Data una L-teoria T , un sottoinsieme S ⊆ T è un insieme di
assiomi per T se S = T .
Data una L-struttura A, come caratterizzare tutti i modelli di Th (A)? Ovvero,
come caratterizzare tutte le L-strutture elementarmente equivalenti ad A?
Un modo per farlo è riuscire a trovare un insieme di assiomi per Th (A).
In altre parole, cerchiamo una sottoteoria T ⊆ Th (A) che sia completa e che
consista in una lista esplicita di enunciati (la cui interpretazione sia, se
possibile, matematicamente “pregna di senso”). Facciamo un esempio.
Esempio 4.2 Supponiamo di voler descrivere Th C con una lista di assiomi
che esprimano delle proprietà facilmente identificabili del campo dei numeri
complessi. Costruiamo dunque pezzo per pezzo una sottoteoria T ⊆ Th C ,
enumerando le proprietà di base di C che ci vengono in mente. Cominciamo
considerando gli assiomi di campo (che abbiamo visto in un esercizio
precedente). Questi enunciati sono sicuramente veri in C poiché C è un campo.
Tuttavia, sappiamo (vedi Esempio 3.1) che esistono modelli degli assiomi di
campo che non sono elementarmente equivalenti a C.
Questo esempio suggerisce di aggiungere alla nostra lista di assiomi una
proprietà del campo dei numeri complessi che il campo dei numeri razionali non
ha: l’essere algebricamente chiuso.
Come tradurre questa proprietà con degli enunciati?
Un solo enunciato non sarà sufficiente. Ce la possiamo fare invece con una lista
numerabile di assiomi: per ogni n ∈ N fissato, possiamo scrivere un enunciato
che dice che, per ogni scelta degli n coefficienti complessi che identificano un
polinomio monico di grado n, il polinomio in questione ha una radice:
∀a0 , . . . , an−1 ∃x x n + an−1 x n−1 + . . . + a0 = 0.
A questo punto abbiamo identificato gli assiomi di campo algebricamente
chiuso e ci chiediamo se abbiamo ottenuto una teoria completa. Esistono
campi algebricamente chiusi che non sono elementarmente equivalenti a C? Un
esempio precedente ci suggerisce che la risposta è sì: consideriamo un campo di
caratteristica diversa da 0 (per esempio, il campo Z/2Z dell’Esempio 3.1).
Nella chiusura algebrica di questo campo (che esiste ed è anch’essa di
caratteristica 2 (*)) si avrà che 1 + 1 = 0, un enunciato che è falso in C.
Aggiungiamo dunque alla nostra lista di assiomi un enunciato per ogni n ∈ N
che dice che la somma di n volte 1 è diversa da zero.
Abbiamo dunque identificato la teoria ACF0 dei campi algebricamente chiusi di
caratteristica zero.
Si tratta di una teoria completa?
Questa domanda è difficile: come stabilire se esiste un enunciato vero in C e un
modello di ACF0 in cui tale enunciato sia falso? Vedremo in seguito alcuni
metodi e criteri per stabilire se una teoria è completa.
Teorema (Tarski). ACF0 è una teoria completa.
Dunque il campo dei numeri complessi è caratterizzato, a meno di elementare
equivalenza, dagli assiomi di campo algebricamente chiuso di caratteristica zero.
Esercizio. Abbiamo già incontrato (di sfuggita...) un altro modello di questa
teoria. Quale?
Descrivere Th C come l’insieme delle conseguenze logiche degli assiomi di
ACF0 ha il vantaggio di identificare delle proprietà algebriche ben note (“essere
un campo”, “essere algebricamente chiuso”, “essere di caratteristica zero”)
come caratterizzanti tutto ciò che si può dire su C al prim’ordine (nel
linguaggio dei campi).
C’è un altro grande vantaggio.
La lista di assiomi che abbiamo fornito è “esplicita” anche nel seguente senso:
esiste una procedura algoritmica che permette di stabilire in un tempo finito se
un dato enunciato sia o meno un assioma della teoria.
Questo fatto ha una conseguenza molto importante, ovvero che
esiste una procedura algoritmica che permette di stabilire in un tempo finito,
dato un qualunque enunciato, se tale enunciato sia o meno conseguenza logica
degli assiomi.
Cerchiamo di dare una spiegazione informale di questo risultato.
Il teorema di completezza ci dice che se un enunciato ϕ è conseguenza logica di
una teoria T , allora esiste una dimostrazione di ϕ a partire dagli assiomi di T .
Una dimostrazione di ϕ non è altro che una successione finita di enunciati (che
termina con l’enunciato ϕ), prodotta a partire dagli assiomi di T grazie alle
regole di deduzione.
Una dimostrazione ha dunque un carattere finitario e algoritmico, se gli assiomi
sono identificabili in maniera effettiva.
Possiamo allora elencare (enumerare) in maniera effettiva tutte le dimostrazioni
a partire dagli assiomi di T e otterremo così un’enumerazione effettiva dei
teoremi (ovvero le conseguenze logiche) di T .
Sia ora ϕ un enunciato, vogliamo stabilire algoritmicamente se ϕ sia o meno un
teorema di T .
Poiché T è completa, sappiamo che esattamente uno dei due enunciati ϕ e ¬ϕ
è un teorema di T .
Percorriamo dunque l’elenco numerato dei teoremi di T : per ogni n ∈ N,
verifichiamo se l’n-simo teorema θn di T è ϕ oppure ¬ϕ.
In caso affermativo, abbiamo finito. Altrimenti, passiamo ad esaminare θn+1 .
Prima o poi (ma non sappiamo quando!) troveremo un n ∈ N tale che θn = ϕ
oppure θn = ¬ϕ, e a quel punto sapremo se ϕ sia un teorema di T oppure no.
Il concetto intuitivo di “algoritmo” o “procedura effettiva” si formalizza in
teoria della ricorsività (macchina di Turing), ma per gli scopi di questo corso la
nozione di “lista finita di istruzioni” sarà sufficiente.
Definizione 4.3
Una L-teoria T è ricorsivamente assiomatizzabile se esiste un insieme di assiomi
S per T e un algoritmo che, dato un L-enunciato ϕ, stabilisce in un tempo
finito se ϕ ∈ S oppure no.
Una L-teoria T è decidibile se esiste un algoritmo che, dato un L-enunciato ϕ,
stabilisce in un tempo finito se ϕ sia conseguenza logica di T oppure no.
Esempio 4.4 Alla luce di questa definizione, possiamo rivedere e formalizzare
l’Esempio 2.11 dicendo che le teorie Th N e Th Z non sono decidibili.
Teorema 4.5
Una teoria ricorsivamente assiomatizzabile e completa è decidibile.
Le ipotesi possono essere indebolite, richiedendo che l’assiomatizzazione sia
solamente ricorsivamente enumerabile.
Esempio 4.6 Da quanto detto fin’ora, segue che la teoria ACF0 è decidibile.
Nel seguito di questo corso considereremo alcuni esempi di strutture
matematiche interessanti e ci chiederemo se le relative teorie complete sono
ricorsivamente assiomatizzabili.
5. Eliminazione dei quantificatori
Abbiamo già osservato che, dato un insieme definibile in una struttura, esistono
infinite formule per definire tale insieme, e che alcune formule sono più semplici
di altre. Cerchiamo di generalizzare e formalizzare questa osservazione.
Definizione 5.1 Data una L-teoria e due L-formule ϕ (x) , ψ (x), diciamo che
ϕ (x) e ψ (x) sono T -equivalenti se vale
T |= ∀x (ϕ (x) ↔ ψ (x)) .
In altre parole, in tutti i modelli di T , ϕ e ψ definiscono lo stesso insieme
definibile.
La situazione che ci interessa è la seguente: data una qualunque L-formula
ϕ (x), cerchiamo una L-formula più semplice ψ (x) che sia T -equivalente a ϕ.
Definizione 5.2 Una L-teoria T ammette l’eliminazione dei quantificatori se
ogni L-formula è T -equivalente a una L-formula senza quantificatori (ovvero a
una combinazione booleana di formule atomiche).
In altre parole, in tutti i modelli di T , gli insiemi definibili sono definibili senza
quantificatori.
Osservazione 5.3(a) Gli insiemi definiti da una formula senza quantificatori
hanno una descrizione geometrica semplice. Prendiamo l’esempio di R.
Consideriamo l’insieme dei coefficienti di un’equazione polinomiale monica di
grado 3 che abbia tre soluzioni reali distinte:
^
2
A = (a, b) ∈ R : ∃x1 , x2 , x3 xi 6= xj ∧
i 6=j
^
i =1,2,3
xi3
+ axi + b = 0 .
A può essere anche definito, grazie alla formula di Cardano, come
A = (a, b) ∈ R2 : 4a3 + 27b 2 < 0 .
Geometricamente, la prima definizione ci costringe a partire da un sottoinsieme
di R5 , ovvero l’insieme semialgebrico
^
(a, b, x1 , x2 , x3 ) ∈ R5 :
xi 6= xj ∧
i 6=j
^
i =1,2,3
xi3 + axi + b = 0
,
e inseguito a proiettare questo insieme sulle prime 2 coordinate, per ottenere A.
La forma geometrica di A non è apparente nel fare questo processo.
La seconda definizione è invece molto più facile da interpretare: per cominciare,
non siamo costretti a salire di dimensione. Inoltre la forma relativamente
semplice della formula ci permette di dare un’interpretazione geometrica
immediata: si tratta di una parte di piano delimitata dalla cuspide
3
2
b=± √
(−a) 2 .
3 3
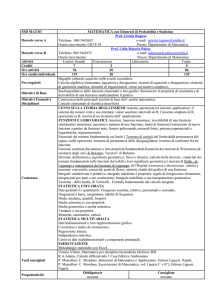
L’insieme A = (a, b) ∈ R2 : 4a3 + 27b2 < 0
b
2
1
0
−4
−3
−2
−1
−1
−2
−3
a
0
1
Osservazione 5.3(b)
Supponiamo di avere una procedura effettiva che, dato un L-enunciato ϕ,
restituisce un L-enunciato ψ senza quantificatori T -equivalente a ϕ.
Supponiamo inoltre di avere una procedura effettiva che, dato un L-enunciato
senza quantificatori ψ, stabilisce se ψ sia o meno conseguenza logica di T .
Allora T è decidibile: combinando le due procedure effettive, si ottiene un
algoritmo di decisione.
Consideriamo
di nuovo R. Come già detto, un risultato di Tarski ci dice che
Th R ammette l’eliminazione dei quantificatori.
Inoltre, la dimostrazione mostra che esiste una procedura effettiva di
eliminazione.
Ora, gli enunciati senza quantificatori non sono altro che combinazioni
booleane di enunciati della forma m = n e m < n (con m, n ∈ Z), la cui verità
o falsità è facilmente verificabile algoritmicamente.
Ne segue che Th R è decidibile.
Osservazione 5.3(c) Sia T una L-teoria incompleta.
È possibile estendere T a una teoria completa: basta considerare un qualunque
modello A di T e la teoria Th (A).
Supponiamo di voler classificare tutti i possibili completamenti di T .
Se A, B sono due modelli di T non elementarmente equivalenti, allora esiste un
enunciato ϕ tale che A |= ϕ e B |= ¬ϕ.
Se T ammette l’eliminazione dei quantificatori, allora possiamo supporre che ϕ
sia senza quantificatori.
Ad esempio, consideriamo la teoria ACF dei campi algebricamente chiusi (di
qualsiasi caratteristica).
Teorema (Tarski). Questa teoria ammette l’eliminazione dei quantificatori.
Da quanto abbiamo detto, la classificazione dei campi algebricamente chiusi a
meno di elementare equivalenza dipende dagli enunciati senza quantificatori.
Nel linguaggio dei campi gli unici enunciati senza quantificatori sono
combinazioni booleane di enunciati della forma m = 0 (con m ∈ Z).
Ne segue che i completamenti di ACF sono interamente determinati dalla
caratteristica dei loro modelli.
Ovvero, tutti e soli i completamenti di ACF sono della forma ACFp (campi
algebricamente chiusi di caratteristica p, dove p è zero o un numero primo).
Proposizione 5.4 Sia K = hK ; 0, 1, +, −, ·i un campo e supponiamo che
Th (K) ammetta l’eliminazione dei quantificatori. Allora ogni sottoinsieme
definibile di K è finito o cofinito.
Dimostrazione. Sia A ⊆ K un sottoinsieme definibile. Per ipotesi, si tratta di
un insieme definibile (con parametri) senza quantificatori. Le formule senza
quantificatori in una variabile libera nel linguaggio dei campi sono combinazioni
booleane di formule della forma
p (x) = 0,
dove p (x) è un polinomio a coefficienti in K . L’insieme {x ∈ K : p (x) = 0} è
un insieme finito (di cardinalità ≤ al grado di p). Una combinazione booleana
di insiemi finiti è un insieme finito o cofinito.
Corollario 5.5 I sottoinsiemi di C definibili in C sono finiti o cofiniti.
In particolare, Calg non è definibile in C.
Definizione 5.6 Una struttura infinita tale che tutti i sottoinsiemi definibili del
dominio sono finiti o cofiniti, è detta minimale.
Una teoria completa i cui modelli siano tutti minimali è detta fortemente
minimale.
Osservazione 5.7 Sappiamo che ACF0 ammette l’eliminazione dei quantificatori
ed è completa (dunque, ACF0 =Th C ). Segue dalla Proposizione 5.4 che
Th C è fortemente minimale.
Nota. L’aggettivo “minimale” significa che i sottoinsiemi definibili del dominio
della struttura sono i più semplici possibile, ovvero definiti da formule senza
quantificatori che coinvolgono unicamente il simbolo “=” (e non gli altri
simboli del linguaggio).
L’avverbio “fortemente” si spiega nel modo seguente: la proprietà di
finitezza/cofinitezza degli insiemi definibili non è esprimibile con un insieme di
enunciati (vedremo in seguito perchè) e non si preserva per elementare
equivalenza.
Ci sono esempi di teorie complete che hanno alcuni modelli minimali e altri
modelli senza questa proprietà.
Esercizio. (*) Calg è un campo algebricamente chiuso di caratteristica zero.
Sia Calg = Calg ; 0, 1, +, −, · |= ACF0 . Poiché la teoria ACF0 è completa, ne
deduciamo che C ≡ Calg .
Di conseguenza, il fatto che C contenga elementi non algebrici (trascendenti)
non può essere espresso con un enunciato del linguaggio dei campi.
Il Teorema di Tarski
Il teorema di Tarski afferma che Th R ammette l’eliminazione dei
quantificatori ed è decidibile. Enunceremo un teorema piùgenerale, che avrà il
vantaggio di fornire un’assiomatizzazione ricorsiva di Th R .
Definizione 5.8 Un campo ordinato K è reale chiuso se vale il Teorema del Valor
Intermedio: per ogni polinomio p (x) a coefficienti in K , se esistono a, b ∈ K
tali che a < b e p (a) · p (b) < 0, allora esiste c ∈ (a, b) tale che p (c) = 0.
Esercizio. Esprimere questa proprietà nel linguaggio dei campi ordinati.
Notazione 5.9 Denotiamo con RCF la teoria dei campi ordinati reali chiusi.
Notiamo che si tratta di una teoria ricorsivamente assiomatizzata.
Teorema 5.10
La teoria RCF ammette l’eliminazione dei quantificatori.
La procedura di eliminazione è effettiva.
Poiché chiaramente RCF ⊆ Th R , si ha che anche Th R ammette
l’eliminazione dei quantificatori effettiva.
Ricorsiva assiomatizzabilità
Corollario 5.11 RCF è una teoria completa.
Dimostrazione (idea). Sia ϕ un enunciato del linguaggio dei campi ordinati.
Dunque ϕ è RCF -equivalente ad un enunciato senza quantificatori, ovvero a
una combinazione booleana di enunciati della forma m = n e m < n (con
m, n ∈ Z). Il valore di verità di questi enunciati è indipendente dalla scelta del
modello di RCF (tali enunciati sono dimostrabili o refutabili a partire dagli
assiomi di RCF ).
Esistono esempi di notevole interesse matematico di campi reali chiusi diversi
dal campo dei numeri reali (ad esempio, alcuni campi di serie formali). Grazie
al Corollario 5.11, tutte le proprietà di R che possono essere espresse come
enunciati del linguaggio dei campi ordinati sono vere in tutti i campi reali
chiusi. Questo principio di transfer della verità degli enunciati da R ad altri
modelli di RCF permette di ottenere automaticamente dei risultati in tali
modelli che sarebbero altrimenti complicati da dimostrare direttamente, non
avendo a disposizione in tali modelli tutti gli strumenti di cui disponiamo in R.
In altre parole, possiamo trasferire la verità di enunciati anche se la
dimostrazione di tali enunciati in R usa argomenti che non sono validi in tutti i
modelli di RCF (dato un enunciato ϕ vero in R, il Corollario 5.11 ci dice che
esiste anche una dimostrazione di ϕ a partire dagli assiomi di RCF , ma non
abbiamo bisogno di trovare tale dimostrazione per concludere che ϕ è vero in
tutti i modelli di RCF ).
Decidibilità
Corollario 5.12 RCF è un’assiomatizzazione ricorsiva di Th R , che è dunque
una teoria decidibile:
esiste una procedura algoritmica per decidere la verità e
la falsità degli L R -enunciati nella struttura R.
Osservazione 5.13 Il corollario ci dice che esiste un algoritmo di decisione. La
dimostrazione di Tarski (eliminazione effettiva dei quantificatori) produce un
tale algoritmo, ma di una tale complessità da renderlo inutile a fini pratici.
Dagli anni ’50 a oggi, numerosi studi si sono concentrati sul produrre algoritmi
di complessità più ragionevole. Risultati di Fischer e Rabin (1974) e di
Davenport e Heinz (1997) hanno mostrato che qualunque algoritmo deve essere
almeno della complessità di una doppia esponenziale nel numero delle variabili.
Un algoritmo di tale complessità è stato dato da Collins (1975, Cylindrical
Algebraic Decomposition). Da allora ne sono stati proposti miglioramenti,
sempre restando nei limiti di complessità imposti dai risultati citati. In
particolare, Weisspfenning e altri si sono concentrati su metodi di decisione per
certe sottoclassi della classe di tutte le formule, in modo da risolvere
determinati problemi in tempo più breve.
Dunque, mostrare con metodi model-teoretici l’esistenza di un algoritmo di
decisione non implica necessariamente di avere a disposizione una procedura
efficace e implementabile a fini pratici.
Definibilità in R
Corollario 5.14 Gli insiemi definibili in R sotto tutti e soli gli insiemi
semialgebrici, ovvero le unioni finite di insiemi della forma
{a ∈ Rn : p (a) = 0, q1 (a) < 0, . . . , qr (a) < 0} ,
dove p, q1 , . . . , qr ∈ R [x].
In particolare, la proiezione di un insieme semialgebrico e il complementare
della proiezione di un semialgebrico sono ancora insiemi semialgebrici.
Grazie alla loro definizione “semplice”, gli insiemi semialgebrici formano una
famiglia di sottoinsiemi di Rn con numerose proprietà geometriche interessanti.
Trattandosi di una famiglia di insiemi definibili in una struttura, tale famiglia è
anche sufficientemente “ricca” da permettere costruzioni non banali.
Osservazione. Riprendiamo l’esempio dell’equazione di secondo grado:
A = (a, b, c) ∈ R3 : R |= a 6= 0 ∧ ∃x ax 2 + bx + c = 0 .
Abbiamo osservato che A è definibile senza quantificatori come
A = (a, b, c) ∈ R3 : R |= b 2 − 4ac ≥ 0 .
Abbiamo anche una formula risolutiva per l’equazione di secondo grado:
√
√
−b + b 2 − 4ac
−b − b 2 − 4ac
x è soluzione ⇔ x =
oppure x =
.
2a
2a
Osserviamo che le soluzioni (viste come funzioni delle variabili a, b, c) sono
definibili.
Ma osserviamo anche che le soluzioni non sono esprimibili come termini del
linguaggio dei campi ordinati: ci mancano il simbolo di divisione e il simbolo di
radice quadrata.
Dunque avere l’eliminazione dei quantificatori non implica saper risolvere le
equazioni come termini del linguaggio.
Cosa succede se espando il linguaggio dei campi ordinati, aggiungendo un
√
simbolo per la divisione e, per ogni n ∈ N, un simbolo per n ?
Posso esprimere le soluzioni delle equazioni polinomiali come termini di questo
linguaggio espanso?
La risposta è NO: parafrasando un teorema di Galois, non tutte le equazioni
polinomiali si risolvono per radicali. Per esempio, per i polinomi di grado 5 non
si ha una formula risolutiva che coinvolga somma, prodotto, quozienti e radici.
Attenzione: se espandiamo il linguaggio con un simbolo di funzione per ogni
soluzione di ogni equazione polinomiale, allora ovviamente in questo linguaggio
espanso tutte le soluzioni di equazioni polinomiali saranno termini! Ma un tale
linguaggio è talmente ricco da essere ingestibile, e dunque non interessante ai
fini di comprendere la natura delle soluzioni.
Resta dunque aperta la seguente questione: esiste un’espansione “ragionevole”
del linguaggio dei campi ordinati in cui le soluzioni delle equazioni polinomiali
siano esprimibili come termini? O più in generale, un’espansione in cui tutte le
funzioni definibili si esprimano come termini?
Viceversa, supponiamo di avere una struttura A in un linguaggio L talmente
ricco che tutte le funzioni definibili si esprimono come termini del linguaggio.
Allora Th (A) ammette l’eliminazione dei quantificatori.
Infatti, dato un insieme definibile B ⊆ An , vogliamo mostrare che B è definibile
senza quantificatori.
Consideriamo la seguente funzione caratteristica
(
1 se x ∈ B
.
χB (x) =
/B
0 se x ∈
Poiché B è definibile in A, si ha che χB è una funzione definibile in A
(esercizio).
Per ipotesi, χB si esprime come un termine del linguaggio L. Dunque la
L-formula
χB (x) = 1
è una L-formula senza quantificatori che definisce l’insieme B.
La relazione d’ordine
Osservazione 5.15 Abbiamo osservato in precedenza che la relazione d’ordine su
R è definibile a partire dalle operazioni di campo.
Ci si potrebbe dunque chiedere se, traducendo gli enunciati di Th R in
formule del linguaggio puro dei campi (senza un simbolo per la relazione
d’ordine) si ottenga una teoria che ammette eliminazione dei quantificatori.
La risposta è negativa (e suggerita dal fatto che per definire la relazione
d’ordine serve un quantificatore).
Infatti, l’insieme definibile a ∈ R : ∃x − a · x 2 = 1 è la semiretta dei numeri
reali negativi, che è un insieme infinito e co-infinito.
Se avessimo eliminazione dei quantificatori nel linguaggio puro dei campi,
questo fatto contraddirrebbe la Proposizione 5.4.
Definibilità in RCF
Si noti che lo stesso argomento vale in qualunque modello R di RCF .
In altre parole, i campi reali chiusi non sono minimali.
Dato un campo reale chiuso R = hR : 0, 1, +, −, ·, <i, come descrivere dunque
i sottoinsiemi di R definibili in R?
Grazie al Teorema di Tarski, sappiamo che si tratta di insiemi definibili senza
quantificatori.
Ovvero, si tratta di combinazioni booleane di insiemi della forma
{x ∈ R : p (x) = 0} e della forma {x ∈ R : p (x) < 0} (dove p (x) è un
polinomio a coefficienti reali).
Gli insiemi del primo tipo sono finiti (si tratta dell’insieme delle radici a1 , . . . , ar
di p (x)).
Gli insiemi del secondo tipo sono, grazie alla proprietà del valore intermedio,
unioni di alcuni degli intervalli aperti (−∞, a1 ) , (a1 , a2 ) , . . . , (ar , +∞).
Dunque i sottoinsiemi di R definibili in R sono unioni finite di intervalli aperti
(limitati o illimitati) e punti.
Strutture o-minimali
Definizione 5.16
Una struttura infinita totalmente ordinata tale che tutti i sottoinsiemi definibili
del dominio sono unioni finite di intervalli e punti, è detta o-minimale.
La “o” in “o-minimale” è un’abbreviazione per “ordine”. In analogia con il caso
minimale, nelle strutture o-minimali i sottoinsiemi definibili del dominio sono
definibili con formule senza quantificatori che coinvolgono unicamente la
relazione d’uguaglianza e la relazione d’ordine (e non gli altri simboli del
linguaggio). Si tratta quindi delle più “semplici” strutture totalmente ordinate.
Come per le strutture minimali, non è possibile esprimere la proprietà di
o-minimalità con un insieme di enunciati (vedremo in seguito perchè).
Tuttavia, a differenza del caso minimale, un teorema di Knight, Pillay e
Steinhorn dimostra che, data una teoria completa T di strutture infinite
totalmente ordinate, se esiste un modello o-minimale di T allora tutti i modelli
di T sono o-minimali.
In questo caso si parla di teoria o-minimale (l’avverbio “fortemente” non è più
necessario).
Funzioni non semialgebriche
Nella struttura R le funzioni definibili sono le funzioni semialgebriche. Esempi
di funzioni algebriche, oltre
p ai polinomi, sono le funzioni razionali (quozienti di
polinomi) e le funzioni p (x), dove p è un polinomio.
Esistono molte funzioni reali interessanti che non sono semialgebriche.
Esercizio. La funzione esponenziale exp (x) = e x non è semialgebrica.
Infatti, grazie al teorema di eliminazione dei quantificatori, se e x fosse definibile
in R allora esisterebbero polinomi p (x, y ) , q1 (x, y ) , . . . , qr (x, y ) tali che
n
2
(x, y ) ∈ R : y = e
x
o
=
n
o
2
(x, y ) ∈ R : p (x, y ) = 0 ∧ q1 (x, y ) < 0 ∧ . . . ∧ qr (x, y ) < 0 .
In altre parole, per ogni x ∈ R, si avrebbe p (x, e x ) = 0 e qi (x, e x ) < 0.
Notiamo che l’equazione p (x, e x ) = 0 deve essere necessariamente presente in
questa presentazione (le condizioni qi < 0 definiscono aperti del piano e non
possono dunque bastare a definire il grafico di e x (*)).
Scriviamo p (x, y ) = an (x) y n + an−1 (x) y n−1 + . . . + a0 (x), dove ai sono
polinomi.
a
a
Sostituendo y = e x , otteniamo an (x) e nx 1 + n−1
(x) e −x + . . . + an0 (x) e −nx = 0.
an
Passando al limite per x → +∞, otterremmo che 1 + 0 + . . . + 0 = 0, un
assurdo.
La struttura Rexp
Definizione 5.17 Consideriamo un’espansione Lexp del linguaggio dei campi
ordinati con un simbolo di funzione unario exp, da interpretare come la
funzione esponenziale, e definiamo in questo linguaggio espanso la struttura
Rexp = hR; 0, 1, +, −, ·, exp, <i .
È possibile ottenere per Th (Rexp ) dei risultati di eliminazione, ricorsiva
assiomatizzabilità,
decidibilità analoghi a quelli che abbiamo presentato per
Th R ? Cercheremo di rispondere a questa domanda nel seguito del corso.
Anticipiamo subito un risultato molto profondo di Wilkie:
Teorema 5.18 La teoria Th (Rexp ) è o-minimale.
In altre parole, tutti i sottoinsiemi di R definibili in Rexp sono unioni finite di
intervalli e punti.
Osservazione 5.19 Per capire la difficoltà di questo risultato, vediamo cosa
sappiamo sui sottoinsiemi di R definibili in Rexp .
Consideriamo dapprima gli insiemi definibili senza quantificatori.
I termini (in una variabile) del linguaggio Lexp sono espressioni molto
complicate:
x 2 e 3x
3
+e 5
− 1; e e
ee
x
− x 5 ; e 3x
2
+4x 6 −e x
2
.
I termini più semplici sono i polinomi esponenziali, ovvero espressioni della
forma
f (x) = p (x, e x ) , dove p ∈ Z [x, y ] .
Notiamo che a priori non sappiamo nemmeno se un’equazione della forma
f (x) = 0 ha o meno un numero finito di soluzioni!
(Si tratta di un risultato difficile di Khovanskii)
Anche conoscendo il risultato di Khovanskii, non sappiamo se Th (Rexp )
ammetta o meno l’eliminazione dei quantificatori. Dunque, a priori gli insiemi
definibili sono molto complicati, e non è chiaro come stabilire se un sottoinsieme
di R definibile in Rexp sia o meno un’unione finita di intervalli e punti.
Insiemi definibili nelle strutture o-minimali
Gli insiemi definibili in strutture o-minimali (di tutte le arietà) hanno delle
proprietà geometriche interessanti. In particolare, molte delle proprietà
geometriche degli insiemi semialgebrici sono vere anche degli insiemi definibili
nelle strutture o-minimali.
Il Teorema 5.18 ha le seguenti conseguenze (che sono anche vere in R) sulla
geometria degli insiemi definbili in Rexp .
Corollario 5.20
• I sottoinsiemi di Rn definibili in Rexp hanno un numero finito di
componenti connesse.
• Le funzioni f : R → R definibili sono continue (derivabili) a tratti (ovvero,
salvo in un numero finito di punti) e hanno un numero finito di zeri.
• (Uniforme finitezza) Sia ϕ (x, y1 , . . . , yn ) una Lexp -formula tale che
∀a ∈ Rn l’insieme Aa = {x ∈ R : Rexp |= ϕ (x, a)} è finito. Allora esiste
N ∈ N tale che ∀a ∈ Rn l’insieme Aā ha al più N elementi.
6. Rapporti tra strutture e model-completezza
Definizione 6.1 Sia L un linguaggio e siano A = hA; . . .i , B = hB; . . .i due
L-strutture tali che A ⊆ B.
A è una sottostruttura di B (e scriviamo A ⊆ B) se:
• per ogni simbolo di costante c, si ha c A = c B ;
• ∀a ∈ An e per ogni simbolo f di funzione n-ario di L, si ha f A (a) = f B (a);
• ∀a ∈ An e per ogni simbolo R di relazione n-ario di L, si ha
a ∈ RA ⇔ a ∈ RB.
In questo caso diciamo che B è un’estensione di A.
Proposizione 6.2 A ⊆ B se e solo se, per ogni L-formula senza quantificatori
ϕ (x) e per ogni a ∈ An si ha
A |= ϕ (a) ⇔ B |= ϕ (a) .
Dimostrazione. (esercizio).
Definizione 6.3 Diciamo che A è sottostruttura elementare di B (e scriviamo
A B) se per ogni L-formula ϕ (x) e per ogni a ∈ An si ha
A |= ϕ (a) ⇔ B |= ϕ (a) .
Osservazione 6.4 Se A B allora A ≡ B. Infatti, basta considerare solo gli
enunciati, nella precedente definizione.
Esempi 6.5 Riprendiamo le strutture degli esempi fatti finora.
• nella notazione dell’Esempio 2.11, abbiamo che N ⊆ Z. Tuttavia, N non è
una sottostruttura elementare di Z. Infatti, N 6≡ Z (esercizio).
• nella notazione dell’Esempio 3.1, abbiamo che hZ/2Z; 0, 1, +, ·i non è una
sottostruttura di hZ; 0, 1, +, ·i. Infatti esiste un enunciato senza
quantificatori sul valore di verità del quale le due strutture non concordano.
alg
C. Infatti, sappiamo che si tratta di modelli della teoria completa
ACF0 , che ammette l’eliminazione dei quantificatori. Dunque, verificare
che Calg C si riduce a verificare che Calg ⊆ C. Quest’ultima verifica è
immediata usando la definizione di sottostruttura.
• C
Definizione 6.6 Una L-teoria è detta model-completa se per ogni A, B |= T con
A ⊆ B si ha che A B.
Osservazione 6.7 Una teoria che ammette l’eliminazione dei quantificatori è
model-completa.
Come verificare se una sottostruttura è elementare?
Teorema 6.8 (Test di Robinson) Una L-teoria T è model-completa se e solo se
ogni L-formula è T -equivalente a una formula esistenziale.
La dimostrazione è rimandata a più tardi.
Corollario 6.9 Nei modelli di una teoria model-completa tutti gli insiemi
definibili sono esistenzialmente definibili, ovvero sono proiezioni di insiemi
definibili senza quantificatori.
Esempio 6.10 Consideriamo la struttura Rf = hR; 0, 1, +, −, ·i (dove abbiamo
omesso la relazione d’ordine). Abbiamo visto che la relazione d’ordine è
esistenzialmente definibile in Rf . Abbiamo anche visto che Th (Rf ) non
ammette eliminazione dei quantificatori.
Tuttavia, questa teoria è model-completa.
Infatti, se L0 è il linguaggio dei campi e L è il linguaggio dei campi ordinati,
ogni L0 -formula è una L-formula e, viceversa, ad ogni L-formula ϕ possiamo
associare una L0 -formula ϕ0 , dove abbiamo sostituito la relazione d’ordine con
la suadefinizione esistenziale. Notiamo che, se θ è un L-enunciato, allora
Th R |= θ ⇔ Th (Rf ) |= θ0 . Ne segue che, se ψ è una L0 -formula, allora ψ è
Th R -equivalente a una L-formula ϕ senza quantificatori. Ne segue che ψ è
Th (Rf )-equivalente alla formula esistenziale ϕ0 .
Vediamo ora che legame c’è tra completezza e model-completezza di una teoria.
Definizione 6.11 Data una L-teoria T , un modello di T che sia una
sottostruttura di tutti gli altri modelli T è detto modello primo.
Esempio 6.12 Calg è un modello primo della teoria ACF0 .
Esercizio. L’insieme Calg ∩ R è il dominio di una struttura Ralg , che è modello
primo di RCF .
Proposizione 6.13 Sia T una L-teoria model-completa. Se T ammette un
modello primo allora T è completa.
Dimostrazione. Sia P un modello primo e siano A, B |= T . Per ipotesi,
P ⊆ A, B e per model-completezza P A, B. Dunque in particolare
A ≡ P ≡ B.
Come conseguenza otteniamo una dimostrazione del Corollario 5.11.
Ancora su Rexp
Teorema. La teoria Texp := Th (Rexp ) non ammette l’eliminazione dei
quantificatori.
Teorema (Wilkie). La teoria Texp è model-completa.
Teorema (Macintyre, Wilkie). Esiste una procedura effettiva per trasformare
una Lexp -formula ϕ in una Lexp -formula esistenziale ψ che sia Texp -equivalente
a ϕ. (∼)
Domanda. Possiamo concludere che Texp è decidibile?
Problema. Non sappiamo se esiste un algoritmo per decidere la verità o falsità
degli enunciati esistenziali.
Addirittura, non sappiamo se esiste un algoritmo per decidere la verità o falsità
degli enunciati senza quantificatori!
Teorema (Macintyre, Wilkie). Se assumiamo una celebre congettura di teoria
dei numeri (congettura di Schanuel), allora Texp è decidibile.
Sempre assumendo la congettura, abbiamo un’assiomatizzazione esplicita per
Texp .
7. Compattezza
• Il teorema di compattezza;
• classi assiomatizzabili;
• non assiomatizzabilità delle strutture o-minimali;
• dimostrazione del Teorema 6.8;
• I teoremi di Löwenheim-Skolem.
Appendice I
Consideriamo l’insieme dei numeri reali con la struttura di campo ordinato
R = hR; 0, 1, +, −, ·, <i.
Sia Ralg l’insieme dei numeri reali che sono soluzione di un’equazione
polinomiale a coefficienti interi, ovvero
Ralg = {a ∈ R : ∃ un polinomio p (z) ∈ Z [z] t.c. p (a) = 0} .
Esercizio. L’insieme delle soluzioni di un sistema di equazioni polinomiali a
coefficienti in Ralg è ∅-definibile in R.
Suggerimento. Sia a ∈ Ralg . Trovare una L R -formula ϕ (x) tale che
{a} = x ∈ R : R |= ϕ (a) .
Una volta fatto ciò, ecco un esempio di come proseguire: consideriamo il
polinomio ax 2 + 2x + 1 e supponiamo di voler dimostrare che l’insieme delle
sue radici è ∅-definibile. Ecco la definizione:
x ∈ R : ax 2 + 2x + 1 = 0 = x ∈ R : ∃y ϕ (y ) ∧ yx 2 + 2x + 1 = 0 .
Osservazione. Consideriamo l’insieme a ∈ C : a2 + 1 = 0 = {i, −i}.
La struttura C non “distingue” le due radici del polinomio x 2 + 1 (vedremo
dopo perchè). In altre parole, {i} non è ∅-definibile.
Non posso dunque fare lo stesso ragionamento con Calg .
Sia Calg l’insieme dei numeri complessi che sono soluzione di un’equazione
polinomiale a coefficienti interi, ovvero
Calg = {a ∈ C : ∃ un polinomio p (z) ∈ Z [z] t.c. p (a) = 0} .
Sia C = hC; 0, 1, +, −, ·i.
Teorema (Tarski). La teoria Th C ammette l’eliminazione dei quantificatori.
Osservazione. Il singoletto {i} non è ∅-definibile in C.
Supponiamo che esista una L C -formula ϕ (x) tale che
{i} = x : C |= ϕ (x) .
Grazie al Teorema di Tarski, possiamo supporre che ϕ (x) sia una formula senza
quantificatori. Mettiamo ϕ (x) in forma normale disgiuntiva: ϕ è dunque una
disgiunzione finita di formule della forma
p1 (x) = 0 ∧ . . . ∧ pk (x) = 0 ∧ q1 (x) 6= 0 ∧ . . . ∧ ql (x) 6= 0,
dove pi , qi ∈ Z [x].
Claim. Affermo che i e −i soddisfano esattamente le stesse relazioni
polinomiali.
Modulo il Claim, è facile ricavare dall’espressione (1) che i e −i soddisfano
esattamente le stesse formule.
(1)
Claim. Affermo che i e −i soddisfano esattamente le stesse relazioni
polinomiali.
Per vedere ciò, ci sono due modi:
- osserviamo che il coniugio di numeri complessi lascia invariati i polinomi a
coefficienti in Z: p (i) = 0 ⇔ p (i) = 0 ⇔ p (−i) = 0.
- alternativamente, usiamo la divisione euclidea per mostrare che, se p (i) = 0,
allora il polinomio p (x) è divisibile per il polinomio x 2 + 1:
p (x) = x 2 + 1 q (x) + r (x) ,
(2)
dove r (x) = ax + b è un polinomio di grado 1. Sostituendo i a x
nell’equazione (2), otteniamo che r (x) è il polinomio nullo (ovvero a = b = 0).
In entrambi i casi, ho dimostrato il Claim.
Osservazione. Il secondo metodo può essere facilmente generalizzato per
dimostrare l’enunciato seguente:
Sia g (x) un polinomio di grado > 1 e sia a ∈ C tale che g (a) = 0.
Allora il singoletto {a} non è ∅-definibile.
Per vedere ciò, basta ripetere il ragionamento qui sopra, facendo giocare al
polinomio minimo di a il ruolo del polinomio x 2 + 1.
Osservazione. Anche il primo metodo può essere generalizzato per dimostrare
l’enunciato qua sopra, ma bisogna conoscere un po’ di teoria di Galois.
Ran
Appendice II: Failure of quantifier elimination for
= hR; +, −, ·, <, {f [−1, 1]n : f real analytic, n ∈ N}i
(Osgood, 1916). y = ϕ (x) transcendental analytic. The cone on y = ϕ (x)
z
E = {(x, y , z) : ∃u 0 ≤ x, z, u ≤ 1, x = uz, y = zϕ (u)}
y
is not quantifier free definable.
x
Suppose E described by an analytic equation F = 0 in a nbd of 0.
P
Then F (x, y , z) =
p (x, y , z), pn homogeneous of degree n.
P n n
0 = F (uz, zϕ (z) , z)=
z pn (u, ϕ (u) , 1)⇒ ∀n pn (u, ϕ (u) , 1) = 0
However,
(Gabrielov, 1968). Ran is model complete and o-minimal.
(Hironaka, 1973; Denef-van den Dries, 1988).
Ran has quantifier elimination in the language L (Ran ) ∪ x 7→ x1 .
Example. The cone : E = (x, y , z) : 0 ≤ x, z ≤ 1, y = zϕ xz .