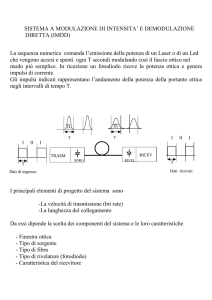
FOTODIODI METALLO-SEMICONDUTTORE
Il problema dell’assorbimento di fotoni nella regione neutra frontale può essere risolto
ricorrendo a diodi metallo-semiconduttore. Se il metallo utilizzato è trasparente o molto
sottile, l’assorbimento in questo strato può essere trascurabile.
Eg > h > q B utile per la rivelazione di fotoni a
bassa energia
h > Eg e V < Vm (pol. inversa), simile al caso del
pin, ma senza regione neutra frontale, utile per la
rivelazione di fotoni ad alta energia ( grande)
h > Eg e V > Vm (pol. inversa), moltiplicazione a
valanga
Fotodiodo Au/Si con strato
antiriflesso in ZnS
Anche i fotodiodi ad eterogiunzione consentono di abbattere in modo considerevole
il numero di fotoni assorbiti nella regione superficiale.
In questo esempio la regione frontale n
è composta da InP, che ha una Eg = 1.3
eV (950 nm), mentre la regione di
assorbimento è in In0.53Ga0.47As con Eg
= 0.73 eV (1670 nm). I fotoni con >
950 nm attraversano l’InP per essere
assorbiti nella rcs, che invece è
trasparente ai fotoni con > 1670 nm.
Per ottenere un’elevata R, è
fondamentale l’assenza di difetti
reticolari all’interfaccia.
P-GaAs
Fotodiodo integrato per =1.55 m
Esempio
Una barra di semiconduttore intrinseco con concentrazione intrinseca trascurabile al
buio è esposta ad una sorgente luminosa.
a) assumendo una generazione uniforme gn=51018 cm-3 s-1, determinare la
conducibilità del semiconduttore. Utilizzare n=p=100 cm2V-1s-1 e n=p=10 s
b) determinare quanto tempo occorre affinché la conducibilità diminuisca di e=2.71
volte dopo lo spegnimento della sorgente luminosa.
Esempio
A causa dell’assorbimento, non è sempre possibile ipotizzare una foto-generazione
uniforme in un semiconduttore. Infatti la generazione vale localmente: gn(x) = gn(0)
exp(- x) in cui è il coefficiente di assorbimento del materiale.
Assumendo che la regione intrinseca è completamente
svuotata, che la generazione superficiale è go=1019 cm-3 s-1,
che l’assorbimento è = 0.01 m-1, che l’area di giunzione
è 1 mm2, calcolare la fotocorrente che si genera nella
regione svuotata.
POLARIZZAZIONE DEL
FOTODIODO
Il modo più semplice di utilizzare un
fotodiodo consiste nel polarizzarlo
inversamente
attraverso
un
resistore, misurando su questo la
caduta prodotta dalla corrente
fotogenerata.
Per correnti elevate c’è il rischio di
portare il dispositivo a funzionare in
polarizzazione diretta (zona non
lineare).
Il guadagno di transimpedenza
per segnali variabili è:
vo
R
i ph 1 sRC J
e quindi per avere elevato guadagno
occorre R grande. Ma questo riduce
la banda passante.
POTENZIALE FOTOVOLTAICO
Un modo alternativo di utilizzare un fotodiodo è quello di misurare la tensione di circuito aperto.
Infatti se si applica una polarizzazione diretta ad un fotodiodo illuminato, si determina una corrente
di portatori maggioritari che ha verso opposto a quello dei portatori minoritari. Il potenziale per il
quale si annulla la corrente attraverso il dispositivo è il potenziale fotovoltaico.
Operando a circuito aperto ID=0 e quindi il potenziale fotovoltaico compare ai capi del dispositivo.
Ponendo ID= 0 nella:
V
I D I Ph I o 1 e nVT
si ottiene:
I Ph
Voc n VT ln1
Io
con IPh >> Io
Quindi il potenziale prelevato ai capi del
fotodiodo aumenta con il logaritmo
dell’intensità luminosa.
circuito di polarizzazione che riduce il
rischio di portare il PD in zona non lineare
I
RI+RL
RL
Iph
V
AMPLIFICATORE A TRANSIMPEDENZA PER FOTODIODO
Un fotodiodo non è un generatore di corrente ideale, e quindi
utilizzando una resistenza per la misura della corrente prodotta
nel fotodiodo, non tutta Iph circolerà in RL, tranne se RL = 0
Utilizzando l’ingresso di un Op.Amp. il fotodiodo
vede un corto virtuale a massa. Quindi:
vo v x
vx
i ph
0
RF
Z CJ
A
dove
da cui
vo
1
A
RF
1 A 1 sC J RF
i ph
1 A
vo Av x
f 3dB
e
ZCJ 1
sC J
1 A
2 RF C J
Lontano dalla frequenza di taglio, il guadagno coincide con quello che si ha con carico
puramente resistivo (RF), mentre la banda è notevolmente aumentata. Se si aumenta il
guadagno agendo su RF , si ha una riduzione della banda.
SENSORI DI POSIZIONE BASATI SU FOTODIODI
Fotodiodi a quadrante:
a) circolare con finestra circolare
b) quadrato con finestra quadrata
c) quadrato con finestra a croce
d) variazione dell’area illuminata in
funzione dello spostamento (o=a, =b, x=c)
Esempio: determinazione della
posizione di una sorgente luminosa
FOTODIODI A VALANGA (APD)
I dispositivi APD sfruttano il meccanismo della moltiplicazione a valanga per amplificare il
segnale ricevuto. Per instaurare tale meccanismo, essi funzionano in condizioni di elevata
polarizzazione inversa.
Come in tutti i dispositivi in cui ha luogo un fenomeno di moltiplicazione a valanga, la
corrente risulta incrementata di un fattore M dato da:
'
M 1 n exp n p dx dx
0
0
w
x
1
in cui w è l’ampiezza della regione di
svuotamento e n , p sono i coefficienti di ionizzazione di elettroni e
lacune.
M
Per n ed p uguali e costanti attraverso la rcs si ottiene:
Si ha breakdown quando wn = 1.
1
1nw
All’aumentare del guadagno, il fenomeno di valanga persiste sempre più a lungo dopo la fine
dello stimolo luminoso, e quindi si riduce la velocità del dispositivo.
Per n = p ed M , il
prodotto guadagno*larghezza di
banda vale approssimativamente:
G * BW
3
tn t p
2
2
con tn = w/vn , tp = w/vp
(v = vel. di sat.)
Nella progettazione e realizzazione degli APD occorre garantire che la moltiplicazione sia
uniforme attraverso la sezione del dispositivo, evitando picchi di campo elettrico
localizzati che possono dar vita a fenomeni di breakdown.
Le correnti di dispersione (leakage) ai bordi della giunzione, e le variazioni del campo
elettrico legate a fenomeni di curvatura, sono limitate attraverso la creazione di anelli di
guardia (guard ring).
Il processo di moltiplicazione è per sua natura statistico perché il parametro M fluttua.
Per questo motivo i diodi APD sono caratterizzati da rumore generalmente molto
elevato.
FOTOTRANSISTOR
Il fototransistor è un dispositivo optoelettronico per la rivelazione di luce molto più
sensibile del fotodiodo. Esso sfrutta il guadagno di corrente interno di un BJT per
amplificare la fotocorrente prodotta dalla radiazione.
La raccolta avviene alla giunzione
base-collettore, che per questo
motivo ha una superficie maggiore
rispetto al caso di un BJT normale.
Il terminale di base normalmente
non è polarizzato, per cui l’effetto
fotovoltaico al diodo B-C (p-n) alza il
potenziale di base riducendo la
barriera alla giunzione E-B.
Ne consegue un aumento dell’iniezione di elettroni da E verso C. La corrente di emettitore è:
I E I ph I ph
- ELEVATO RUMORE
- BASSA VELOCITA’ (grande area)
Charge Coupled Devices - CCD
L’applicazione più comune dei CCD è
nei sensori di immagini. Il sensore è
organizzato come un array di singoli
sensori (condensatori MOS o fotodiodi)
parzialmente esposti alla radiazione.
I fotoni incidenti generano localmente
coppie e-h che vengono separati dal
campo. Il numero di elettroni
accumulati è funzione dell’intensità
luminosa, della sua composizione
spettrale e del tempo di esposizione.
La struttura periodica consente
trasferimento degli elettroni lungo
riga, in fondo alla quale è presente
“dispositivo di misura”, in grado
convertire il numero di elettroni in
potenziale.
il
la
un
di
un
La generazione termica concorre ad accumulare elettroni nei pixel, per cui ogni sensore
deve essere svuotato prima dell’esposizione ed il tempo di esposizione deve essere breve.
Durante il trasferimento in cascata, la cui velocità spesso dipende dal tempo di
svuotamento dell’horizontal CCD, i pixel sono ancora esposti alla radiazione (smear).
Alla fine della catena la carica è trasferita ad
un condensatore composto da una regione
n+ isolata (floating), che converte la carica
in un livello di tensione. Ad ogni lettura il
condensatore deve essere scaricato (reset
noise).
quattro fasi
tre fasi
due fasi
SENSORI DI IMMAGINI INTEGRATI
La dimensione massima del sensore (array di pixel) è
imposta dal processo fotolitografico (step-and-repeat).
La tecnologia più diffusa è quella basata su CCD.
Qmax=250.000 e/pixel
Q.E.=15% a 550 nm
fattore di conversione= 5 V/e Jdark=1.2 nA/cm2 (a 60°C)
SENSORI INTEGRATI DI IMMAGINI
Negli ultimi anni si stanno diffondendo sensori di immagini
basati su pixel attivi (APS) compatibili con la tecnologia CMOS.
- minore potenza dissipata
- integrazione con elettronica periferica
- maggiore sensibilità (pixel amplificati)
- funzionamento a basse tensioni ( anche sotto 3.3 V)
- minore risoluzione spaziale
- più elevate correnti di buio
fotodiodo
VDD
Output
Funzionamento:
1) il fotodiodo viene precaricato ad una tensione inversa nota
(reset)
2) durante l’esposizione la fotocorrente scarica parzialmente il
fotodiodo. La scarica è proporzionale al segnale luminoso.
3) il livello finale di tensione è amplificato da M2
cella 55 m2
tecnologia 0.5 m
SENSORI INTEGRATI DI IMMAGINI A COLORI
sensori a matrice RGB
sensori stacked a film sottile
dalla proporzione fra i segnali misurati
sui tre canali è possibile risalire al colore
PIROMETRO
Un pirometro è un sensore che consente di risalire alla temperatura di un oggetto
attraverso la misura a distanza dell’energia emessa da esso.
Alla fine dell’800 il fisico Stefan documentò la relazione esistente fra la radiazione
emessa da una superficie nera e la sua temperatura. Simultaneamente Boltzmann
ricavò teoricamente la stessa relazione per un corpo nero:
E Wm T
2
4
con T in K e = 5.67 10-8 W m-2 K-4 (costante di StefanBoltzmann)
Nel 1900 Plank descrisse la distribuzione spettrale della radiazione emessa:
E T , Wm m
2
1
A
B
5
T
e 1
Ovviamente:
con A=3.74 108 W m4 m-2
B=1.44104 m K (nel vuoto)
E T , d T
0
4
Un pirometro è un sensore di radiazione IR
(fotodiodo, termocoppia, ...) che misura la
potenza emessa da un corpo per unità di
superficie in un dato intervallo di (p.e s fino
a 12 m). Cioè:
Emis
2
1
A
e
5
B
T
1
d
da cui è in principio possibile risalire alla
T. Purtroppo nessun materiale è un corpo
nero, per cui occorre introdurre un coeff.
di
emissività
(,T)
nell’integrale,
coefficiente quasi mai noto con precisione.
densità spettrale di emissione del corpo nero
Nell’ipotesi di costante, il valore di T si
può ricavare eseguendo due o più misure
in diversi intervalli di (two-color
pyrometer).
La precisione è piuttosto bassa: 1%
RUMORE NEI DISPOSITIVI A SEMICONDUTTORE
Con il termine “rumore” (noise) si intendono le fluttuazioni spontanee della
corrente che attraversa un dispositivo, o della tensione ai suoi capi. Poiché
molti dispositivi sono utilizzati con segnali molto deboli (p.es. gli
amplificatori), tali fluttuazioni pongono un limite all’ampiezza minima dei
segnali trattabili.
Una sorgente di rumore viene modellata come un generatore equivalente.
Le prestazioni in termini di rumore sono in genere fornite con riferimento ad
un rumore equivalente in ingresso (equivalent input noise signal), ed il
circuito in cui si genera il rumore viene studiato separando la sorgente dal
circuito stesso:
Le sorgenti di rumore non hanno polarità e non si sommano algebricamente,
si sommano però in potenza. In caso di sorgenti scorrelate:
Anche se il valore medio del rumore è normalmente nullo, la sua presenza
determina in ogni caso una dissipazione di potenza sui carichi resistivi,
essendo la potenza proporzionale al valore quadratico medio (RMS) del
segnale.
Meccanismo fondamentale di formazione del rumore
La densità di corrente in un conduttore vale:
J qnv
Se n e v cambiano nel tempo in modo non correlato, si avrà:
dJ
2
qv dn
qn
2
dv
2
I principali rumori sono Thermal noise, Flicker noise, Shot noise
Il rumore termico è causato, nei semiconduttori e nei conduttori, dal moto
casuale dei portatori. Il valore quadratico medio è calcolabile da:
Vn2 4kTBR
in cui B è la banda [Hz] considerata e R è la resistenza del dispositivo. In
termini di corrente:
I
2
n
4kTB
R
POTENZA DI RUMORE
La potenza del rumore prodotto da un resistore è la potenza che si dissipa su
un carico resistivo RL di valore pari alla resistenza interna del generatore
equivalente di rumore, RS:
vo
vn
2
vn
4
kTRB
2
2
vo
4
Po
kTB
RL
RL
R
Calcolo del rumore termico in un resistore da 1 kohm
A 25°C (298 K)
J
vt2 4 1.38 10 23 298K 1Hz 1000
K
1.64 10 17 W 1.64 10 17 V 2
vt (rms )
A 77 K (azoto liquido)
vt2 4 nV
vt (rms)
vt2 2 nV
Il rumore Flicker ha una distribuzione spettrale del tipo 1/f con 1, per
cui è importante alle basse frequenze. La causa risiede in genere negli effetti
di superficie (difetti o trappole superficiali).
Il rumore Shot costituisce in genere la sorgente maggiore di rumore nei
dispositivi a semiconduttore in cui è presente una giunzione. E’ indipendente
dalla frequenza, tranne che alle altissime frequenze.
Ha due componenti:
- rumore da diffusione termica, generato dagli urti dei portatori con il
cristallo (simile al rumore termico)
- rumore da generazione-ricombinazione
Entrambi i fenomeni danno origine a correnti di “rilassamento” che, a
seguito dei due fenomeni, si creano spontaneamente per garantire la
stazionarietà delle condizioni al contorno (imposte dalla polarizzazione).
Il valore quadratico medio dello Shot noise è calcolabile, a frequenze basse, da:
I
2
n
4 Aq 2 Dn
Ln
n p n po n po 4 Aq 2 Dn n p n po n po
B
3
2
6
2
Ln
generazione-ricombinazione
diffusione termica
dove np è la concentrazione di elettroni iniettati nella regione P (ad x=0), npo
è la concentrazione di equilibrio, e B è la larghezza della banda di interesse.
In polarizzazione diretta si ha:
I n2
2 Aq 2 Dn
n p n po 2qI 2 I o
B
Ln
In polarizzazione inversa si ha:
I n2
B
2qI o
Altre due forme di rumore sono il BURST NOISE (dovuto alla contaminazione
di ioni pesanti, come Au), ed l’AVALANCE NOISE (presente nei dispositivi in
cui si hanno fenomeni a valanga).
Sorgenti di rumore nel BJT
- Shot noise nella corrente di collettore
- Shot, Flicker e Burst noise nella corrente di base
- Thermal noise nel resistore di base