1 Un corpo di massa m = 0.5Kg

1
Esercizio
(tratto dal Problema 4.29 del Mazzoldi 2)
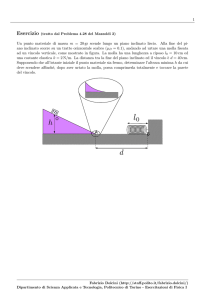
Un corpo di massa m = 0.5 Kg è agganciato ad un supporto fisso tramite una molla di costante
elastica k = 2 N/m; il corpo è in quiete nel punto O di un piano orizzontale, che è liscio a destra di O
e scabro a sinistra di O. Viene impressa al corpo una velocità v0 = 0.16 m/s verso destra. Calcolare:
1. di quanto è allungata la molla nell’istante in cui il corpo si ferma.
Il corpo ripassa per O con velocità −v0 e si ferma dopo aver percorso una distanza di 5 cm alla sinistra
di O. Calcolare
2. il valore del coefficiente di attrito dinamico µ.
m
O
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
2
SOLUZIONE
DATI INIZIALI
m = 0.5 Kg
k = 2 N/m
v0 = 0.16 m/s
|∆l0 | = 0.05 m
1. La prima parte del moto si svolge dal punto O al punto A, in cui il corpo si arresta alla destra
di O.
l0
lA
m
A
O
In questa fase il corpo è soggetto alla sola forza elastica della molla. Indicando con l la coordinata
lungo il piano
F (l) = −k(l − l0 )
(1)
dove l0 è la lunghezza a riposo della molla. Possiamo risolvere il problema in due modi
Primo modo (Bilancio energetico)
Dato che la forza della molla è conservativa, possiamo applicare il teorema di conservazione
dell’energia meccanica:
in
f in
Em
= Em
(2)
dove l’energia meccanica è data da
Em =
1
mv 2 +
2
| {z }
en. cinetica
1
k(∆l)2
2
| {z }
∆l = l − l0
(3)
en. potenz. elastica
Inizialmente la molla è a riposo (il punto materiale si trova in l = l0 ) e quindi
1
in
Em
= mv02
2
(4)
mentre quando il punto materiale si arresta si ha
1
f in
Em
= k(∆lmax )2
2
(5)
Inserendo (4) e (5) in (2) otteniamo
1
mv 2
2 0
=
1
k(∆lmax )2
2
r
⇒ ∆lmax =
m
v0
k
(6)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
3
Sostituendo i valori numerici si ottiene
r
m
v0 =
k
s
0.5 Kg
m
0.16
N
s
2m
∆lmax =
=
uso N = Kg m/s2
s
0.25 Kg
m
=
0.16 =
Kg
s
s2
√
m
=
0.25 s2 0.16 =
s
= 0.08 m
(7)
Secondo modo (Equazioni della dinamica):
Nel tratto da O ad A l’unica forza che agisce sul punto materiale è la forza elastica della molla.
Denotiamo con l la coordinata del punto materiale (l’origine l = 0 è situata nel punto in cui la
molla è agganciata al supporto). Quindi abbiamo
ma = F
⇓
m
d2 l
= −k(l − l0 )
dt2
⇓
d2 l
= −
dt2
k
(l − l0 )
m
(8)
Questa è l’equazione differenziale che dobbiamo risolvere, con le condizioni iniziali (relative
all’istante in cui il punto materiale parte da O verso destra)

l(t = 0)
= l0


(9)

 dl (t = 0) = v
0
dt
Per risolvere l’Eq.(32) osserviamo che è simile all’equazione di un moto armonico
d2 l
= −ω 2 l
dt2
(10)
di cui sono note le soluzioni. Osservando che l0 è costante possiamo scrivere
d2 (l − l0 )
dt2
= −
k
(l − l0 )
m
(11)
da cui, definendo
ω2 =
k
m
(12)
e introducendo la variabile
l0 (t) = l(t) − l0
(13)
d2 l0
dt2
(14)
otteniamo
= −ω 2 l0
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
4
che è l’equazione del moto armonico, la cui soluzione generale si può scrivere
l0 (t) = A cos(ωt) + B sin(ωt)
(15)
Ricordando la relazione (13) otteniamo la soluzione generale dell’Eq.(8)
r
l(t) = l0 + A cos(ωt) + B sin(ωt)
ω=
k
m
Le costanti A e B si determinano imponendo le condizioni iniziali (9)

l(t = 0)
= l0 + A cos(ω 0) + B sin(ω 0) = l0


ossia

 dl (t = 0) =
dt

 A

(16)
(17)
−Aω sin(ωt) + Bω cos(ωt)|t=0 = v0
= 0
(18)
Bω = v0
⇒B=
v0
ω
Sostituendo i valori di A e B nella soluzione generale (16) otteniamo
r
v0
l(t) = l0 +
sin(ωt)
ω
ω=
k
m
(19)
e la velocità è
dl
= v0 cos(ωt)
(20)
dt
Denotiamo ora con tA l’istante in cui il punto materiale raggiunge il punto A di massimo allungamento della molla. Tale punto è caratterizzato dall’annullarsi della velocità
π
v(tA ) = v0 cos(ωtA ) = 0
⇒ ωtA =
(21)
2
La coordinata del punta A è dunque
v0
lA = l(tA ) = l0 +
sin(ωtA ) =
ω | {z }
v(t) =
=+1
v0
= l0 +
ω
Ricordando la definizione (12) otteniamo che l’allungamento
v0
∆lmax = lA − l0 =
=
ω
r
m
=
v0
k
Sostituendo i valori numerici si ottiene
r
m
∆lmax =
v0 =
k
s
0.5 Kg
m
=
0.16
N
s
2m
uso N = Kg m/s2
s
0.25 Kg
m
=
0.16 =
Kg
s
s2
√
m
=
0.25 s2 0.16 =
s
= 0.08 m
(22)
(23)
(24)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
5
2. Il secondo tratto del moto va da quando il corpo ripassa per O con velocità −v0 a quando si
arresta dalla parte scabra del piano (a sinistra di O) in un punto che indichiamo con B. Anche
l0
lB
m
B
O
qui possiamo procedere in due modi:
Primo modo (Bilancio energetico):
In questo tratto le forze che agiscono sul punto materiale sono la forza elastica della molla e
l’attrito dinamico del piano scabro. Dato che quest’ultima forza non è conservativa, l’energia
meccanica non si conserva. Possiamo tuttavia applicare il teorema dell’energia meccanica (NB:
non il teorema di conservazione dell’energia meccanica!)
∆Em = Wnc
(25)
dove ∆Em è la variazione dell’energia meccanica e Wnc è il lavoro delle forze non conservative
(in questo caso l’attrito dinamico). Nel tratto da O a B abbiamo dunque
Z B
O→B
∆Em
=
F~att · d~l
(26)
O
La variazione di energia meccanica vale
O→B
∆Em
= Em;B − Em;O =
1
1
0 2
2
=
0 + k(∆l ) −
m(−v0 ) + 0 =
2
2
1
1
=
k(∆l0 )2 − mv02
2
2
(27)
dove ∆l0 = lB − l0 e lB è la coordinata del punto B.
Siccome la forza di attrito si oppone sempre al moto ed è costante in modulo abbiamo
Wnc = −|F~att ||∆l0 | = −µ mg|∆l0 |
(28)
Si noti che il lavoro è negativo, e quindi l’energia meccanica diminuisce passando da O a B [vedi
Eq.(26)], come è intuitivo aspettarsi in presenza di forze dissipative quali l’attrito.
Inserendo le Eq.(27) e (28) in (25) otteniamo
1
1
k(∆l0 )2 − mv02 = −µ mg|∆l0 |
2
2
(29)
da cui il coefficiente di attrito vale
µ =
− 12 k(∆l0 )2
mg|∆l0 |
1
2
2 mv0
(30)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
6
Inserendo i valori numerici otteniamo
µ =
1
2 0.5 Kg
2
N
0.16 ms − 21 2 m
(−0.05m)2
=
0.5 Kg 9.81 sm2 · 0.05 m
[uso N = Kg m/s2 ]
2
=
0.25 · 0.0256 Kgs2m −
0.24525
Kg
s2
Kg m2
s2
· 0.0025m2
=
= 0.016
(31)
Secondo modo (Equazioni della dinamica):
Nel tratto da O a B la forza di attrito è diretta verso destra, dato che si oppone al moto verso
sinistra. Denotiamo con l la coordinata del punto materiale (l’origine l = 0 è situata nel punto
in cui la molla è agganciata al supporto). Quindi abbiamo
ma = F
⇓
m
d2 l
dt2
= −k(l − l0 ) + µmg
⇓
d2 l
dt2
= −
k
(l − l0 ) + µg
m
(32)
Questa è l’equazione differenziale che dobbiamo risolvere, con le condizioni iniziali (relative
all’istante in cui il punto materiale parte da O verso sinistra)

l(t = 0)


= l0

 dl (t = 0) = −v
0
dt
(33)
Per risolvere l’Eq.(32) osserviamo che è simile all’equazione di un moto armonico
d2 l
= −ω 2 l
dt2
(34)
di cui sono note le soluzioni. Cerchiamo pertanto di ricondurre l’eq.(32) alla forma (34). A
tale proposito osserviamo che il termine in l0 e il termine µg sono entrambi costanti e possono
dunque essere accorpati. Per cui riscriviamo (32) come
d2 l
k µmg l
−
(l
+
)
=
−
0
dt2
m
k
Definendo ora
r
ω=
e
l00 = l0 +
(35)
k
m
(36)
µmg
k
(37)
l’Eq.(35) diventa
d2 l
= −ω 2 l − l00
2
dt
(38)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
7
che è l’equazione di una molla con la stessa costante elastica ma una lunghezza a riposo diversa
(l00 anziché l0 ).
In sostanza
Forza elastica di una
molla con lunghezza
a riposo l0
Forza elastica di una
+
Forza costante
⇔ molla con lunghezza
a riposo l00
Siccome l00 è costante, dall’Eq.(38) segue che
d2 (l − l00 )
2
0
=
−ω
l
−
l
0
dt2
(39)
l0 (t) = l(t) − l00
(40)
d2 l0
= −ω 2 l0
dt2
(41)
ossia la variabile
soddisfa l’equazione del moto armonico
la cui soluzione generica si può scrivere nella forma
l0 (t) = A cos(ωt) + B sin(ωt)
(42)
Dall’Eq.(40) otteniamo dunque la soluzione generale dell’equazione differenziale (32)
l(t) = l00 + A cos(ωt) + B sin(ωt)
(43)
e ricordando l’espressione (37) per l00 otteniamo
r
µmg
l(t) = l0 +
+ A cos(ωt) + B sin(ωt)
k
ω=
k
m
(44)
Le costanti A e B sono da determinarsi imponendo le condizioni iniziali (33)

µmg

l(t = 0)
= l0 +
+ A cos(ω 0) + B sin(ω 0) = l0


k


 dl (t = 0) =
dt
ossia

 A

(45)
−Aω sin(ωt) + Bω cos(ωt)|t=0 = −v0
= − µmg
k
(46)
Bω = −v0
⇒B=
− vω0
Sostituendo le costanti A e B nella soluzione generale (44) otteniamo
µmg µmg
v0
l(t) = l0 +
−
cos(ωt) −
sin(ωt)
k
k
ω
r
ω=
k
m
(47)
La velocità è data dunque da
v(t) =
dl
µmgω
=
sin(ωt) − v0 cos(ωt)
dt
k
(48)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
8
Denotiamo con tB l’istante in cui il punto materiale raggiunge il punto B. Tale punto è caratterizzato dall’annullarsi della velocità
v(tB ) =
µmgω
sin(ωtB ) − v0 cos(ωtB ) = 0
k
(49)
e dunque
v0 k
µmgω
tan(ωtB ) =
Ricordando le formule di trigonometria


cos α =






 sin α
=
√
√
(50)
1
1 + tan2 α
tan α
1 + tan2 α
e utilizzando la (50) ricaviamo



cos(ωtB ) =













sin(ωtB )





=
r
1+
1
v0 k
µmgω
2
(51)
v0 k
µmgω
r
1+
v0 k
µmgω
2
da cui possiamo ricavare la posizione del punto B
µmg µmg
v0
−
cos(ωtB ) −
sin(ωtB ) =
k
k
ω
v0 k
µmg µmg
1
v0
µmgω
r
l0 +
−
2 − ω r
2 =
k
k
v0 k
v0 k
1 + µmgω
1 + µmgω
1
µmg µmg
v02 k 2
r
−
l0 +
2 1 + (µmgω)2 =
k
k
v0 k
1 + µmgω
s
µmg µmg
v0 k 2
l0 +
−
1+
=
k
k
µmgω
s
µmg
1
v0 k 2
2
l0 +
−
(µmg) +
=
k
k
ω
lB = l(tB ) = l0 +
=
=
=
=
[uso ω 2 = k/m]
p
µmg − (µmg)2 + kmv02
= l0 +
k
da cui
p
(µmg)2 + kmv02
(52)
k
Dato che conosciamo ∆l0 come dato dal problema, tale equazione ci permette di determinare µ.
µmg −
.
∆l = lB − l0 =
0
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
9
Esplicitamente, da (52) otteniamo
µmg
∆l −
k
0
p
= −
(µmg)2 + kmv02
k
⇓
∆l0 −
µmg 2
µmg
+
k
(µmg)2
k
=
(µmg)2 + kmv02
k2
⇓
(∆l0 )2 − 2∆l0
k2
=
(µmg)2 + kmv02
k2
⇓
(∆l0 )2 − 2∆l0
µmg
k
=
mv02
k
⇓
2∆l0
µmg
k
= (∆l0 )2 −
mv02
k
⇓
µ =
ossia
µ=
k
2∆l0 mg
mv02
0 2
(∆l ) −
k
1
0 2
2 k(∆l )
− 21 mv02
mg∆l0
(53)
(54)
Sostituendo i valori numerici (ricordiamo che ∆l0 = −0.05 m) otteniamo
µ =
1
2
2
N
2m
(−0.05m)2 − 21 0.5 Kg 0.16 ms
0.5 Kg · 9.81 sm2 · (−0.05 m)
=
[uso N = Kg m/s2 ]
=
Kg
s2
2
· 0.0025 m2 − 0.25 · 0.0256 Kgs2m
= 0.016
2
−0.24525 Kgs2m
=
(55)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I