1
Esercizio
(tratto dal Problema 4.7 del Mazzoldi 2)
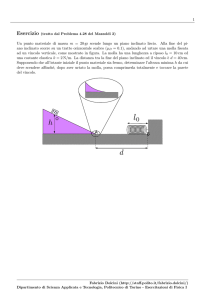
Un punto materiale di massa m è sospeso tramite un filo verticale ed è collegato al suolo da una
molla, di costante elastica k = 70 N/m, che si trova alla lunghezza di riposo l0 . La tensione del filo è
T = 4.9 N. Il filo viene ora tagliato.
m
l0
Calcolare:
1. la massima distanza percorsa dal punto;
2. la posizione in cui la velocità è massima;
3. il valore massimo della velocità.
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
2
SOLUZIONE:
Dati iniziali:
k
T
= 70 N/m
= 4.9 N
Prima che il filo venga tagliato, la molla non esercita alcuna forza sul punto materiale (dato che la
T�
m
m�g
molla è in condizioni di riposo). Il punto materiale è dunque fermo per l’equilibrio tra la forza peso e
la tensione T del filo. Pertanto in modulo abbiamo
T
= mg
⇒ m=
T
g
(1)
Quando si taglia il filo, il punto materiale è soggetto alla forza peso e alla forza elastica della molla.
Per trovare le quantità richieste possiamo procedere in due modi:
PRIMO MODO (Bilancio Energetico):
Le forze che agiscono sul sistema sono (lungo la direzione verticale, asse z verso l’alto)
F = −mg
forza peso
forza elastica
F = −k(z − l0 )
Siccome sono forze conservative, l’energia meccanica è conservata. L’energia meccanica in questo
sistema è data da:
energia cinetica + en. potenz. gravitazionale + en. potenz. elastica
|
{z
}
|
{z
}
|
{z
}
mgz
1
mv 2
2
k
(z−l0 )2
2
1. Trovare la massima distanza percorsa dal punto materiale corrisponde a trovare di quanto si
comprime la molla rispetto alla lunghezza iniziale (=lunghezza a riposo). All’istante iniziale la
velocità è nulla e la molla si trova nella posizione di riposo (z = l):
1
1
in
Em
= mv 2 + mgl0 + k(l0 − l0 )2
2
| {z }
|2
{z
}
=0
(2)
=0
All’istante in cui il corpo raggiunge l’altezza minima (la molla non è necessariamente compressa
completamente!) la velocità è nuovamente nulla. Denotando con
z ∗ = altezza minima raggiunta
(3)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
3
z
z⇤
abbiamo
m l0
1
1
f in
Em
= mv 2 + mgz ∗ + k(z ∗ − l0 )2
2
|2 {z }
(4)
=0
Per la conservazione dell’energia meccanica si ha
in
f in
Em
= Em
1
mgl0 = mgz ∗ + k(z ∗ − l0 )2
2
1
⇒
k(z ∗ − l0 )2 + mg(z ∗ − l0 ) = 0
2
1
∗
∗
(z − l0 )
k(z − l0 ) + mg = 0
2
(5)
Abbiamo due soluzioni
(a) z ∗ − l = 0
⇒
z∗ = l
(corrisponde all’istante iniziale, in cui infatti l’energia cinetica è nulla)
(b)
1
∗
2 k(z
− l) + mg = 0
⇒
z ∗ − l0 = − 2mg
k
| {z }
∆z
− 2mg
k
da cui ∆z =
(negativo perché la molla è compressa verso il basso) Sostituendo i valori numerici otteniamo
2mg
2T
=−
=
k
k
2 · 4.9 N
−
=
N
70 m
= −0.14 m
∆z = −
(6)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
4
2. Per determinare l’altezza z̄ a cui il corpo raggiunge la velocità massima posso procedere in due
modi
• Primo modo (sfrutto la conservazione dell’energia)
La conservazione dell’energia meccanica vale istante per istante. Ad un generico istante il
punto materiale si trova ad un data altezza z e abbiamo
1
1
Em (z) = mgz + mv 2 + k(z − l0 )2
2
2
(7)
e per la conservazione dell’energia
in
Em
= Em (z)
∀z
1
1
mgl = mgz + mv 2 + k(z − l0 )2
2
2
da cui
(8)
1
1
mv 2 = − k(z − l02 + mg(l0 − z)
2
2
e dunque
r
k
(z − l0 )2 + 2g(l0 − z)
(9)
m
(dove abbiamo scelto il segno − davanti alla radice quadrata perché stiamo considerando
la fase in cui il punto materiale scende).
v(z) = − −
Controllo dimensionale:
k
(z − l)2
m
=
[2g(z − l)] =
N
Kg m
m2
m2 = 2
m= 2
m Kg
s Kg
s
2
m
m
m= 2
s2
s
(10)
(11)
OK
Il punto z̄ in cui la velocità è massima è dato dalla soluzione di
dv
dz
=
0
− 2k
m (z̄ − l0 ) − 2g
− q
k
2 −m
(z̄ − l0 )2 + 2g(l − z̄)
=
0
2k
(z̄ − l0 ) + 2g
m
=
0
⇒ z̄ − l0 = −
mg
k
(12)
Lo scostamento vale dunque
∆z = −
mg
T
=−
k
k
(13)
Sostituendo i valori numerici
∆z = −
mg
4.9 N
=− N =
k
70 m
= −0.07 m
(14)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
5
• Secondo modo (sfrutto la dinamica)
La velocità è massima quando l’accelerazione è nulla, ossia quando la somma delle forze che
agiscono sul corpo è nulla. Dunque l’altezza in cui la velocità è massima viene raggiunta
all’altezza z̄ (incognita) alla quale la forza elastica e la forza peso si bilanciano esattamente:
−k(z̄ − l0 )
| {z }
−mg
| {z }
=0
forza elastica
forza peso
(verso l’alto)
(verso il basso)
⇒
z̄ − l0 = −
mg
k
(15)
Lo scostamento vale dunque
∆z = −
mg
T
4.9 N
= − = − N − 0.07 m
k
k
70 m
(16)
3. Il valore massimo della velocità è dato da
vmax = v(z̄) =
r
k
= − − (z̄ − l0 )2 + 2g(l0 − z̄) =
m
[usiamo z̄ − l0 = − mg
k ]
r
k (mg)2
mg
= − −
+ 2g
2
m
k
k
r
mg 2
mg 2
= − −
+2
k
k
r
2
mg
= −
k
[usiamo T = mg]
r
Tg
= −
k
(17)
Sostituendo i valori numerici
s
m 4.9 N
=
N
s2 70 m
r
9.81 · 4.9 m 2
= −
=
70
s
m
= −0.83
s
vmax = − 9.81
(18)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
6
SECONDO MODO (Equazione del moto):
Si parte dalle equazioni della dinamica
F
Fpeso + Fel
= ma
d2 z
= m 2
dt
(19)
d2 z
− mg −k(z − l0 ) = m 2
| {z }
dt
forza elastica
Osserviamo che
se z < l la forza elastica è pos → diretta verso l’alto
se z > l la forza elastica è neg → diretta verso il basso
Pertanto abbiamo l’equazione differenziale
m
d2 z
= −k(z(t) − l0 ) − mg
dt2
(20)
Lo scopo è trovare la soluzione z(t) di tale equazione, con le condizioni iniziali
z(t = 0)
dz
dt (t
= l
(all’inizio il punto si trova a z = l)
(21)
= 0) = 0
(parte con velocità nulla)
Per risolvere l’equazione differenziale (21) procediamo in questo modo
• Osserviamo che la (21) si può riscrivere come
m
d2 z
dt2
= −k(z − l0 ) −mg =
| {z } | {z }
peso
forza elastica
mg
= −k z − l0 −
=
| {z k }
= −k(z − l00 )
con
l00 = l0 −
(22)
mg
k
(23)
In tal modo l’Eq.(21) acquista la forma
m
d2 z
= −k(z − l00 )
dt2
(24)
che rappresenta l’equazione del moto per un punto materiale soggetto ad una molla efficace con
la stessa costante elastica k, ma con una lunghezza a riposo l00 anziché l0 .
Abbiamo pertanto ricondotto il problema a quello di una molla efficace che ingloba sia la molla
originaria che la forza peso
Forza elastica di una
molla con lunghezza
a riposo l0
+
Forza costante
(= −mg)
Forza elastica di una
⇔ molla con lunghezza
a riposo l00 = l0 − mg/k
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
7
• Osservando che l00 è una costante, possiamo introdurre una variabile z 0 traslata
z 0 (t) = z(t) − l00
(25)
⇓
d2 z 0
dt2
=
d2 (z − l00 )
d2 z
=
dt2
dt2
e l’Eq.(25) acquista la forma
m
d2 z 0
= −kz 0
dt2
• Definendo ora
ω2 =
(26)
k
m
(27)
l’equazione (27) diventa
d2 z 0
+ ω2z0 = 0
dt2
(28)
che è l’equazione del moto armonico, le cui soluzioni sono ben note, e sono della forma
z 0 (t) = A cos(α + ωt)
(29)
In conclusione, ricordando la relazione (26) e l’espressione (24) per l00 , abbiamo
r
mg
k
z(t) = l0 −
ω=
+ A cos(α + ωt)
k
m
(30)
Questa è la soluzione generale dell’Equazione differenziale (21). E’ generale nel senso che le
costanti A e α possono essere arbitrarie.
• Il valore delle costanti A e α si determina imponendo che la soluzione generale soddisfi le particolari condizioni iniziali (22). Dunque abbiamo
mg
z(t = 0) = l0 − k + A cos α = 0
(31)
dz
(t
=
0)
=
−A
sin(α
+
ωt)|
=
−A
sin
α
=
0
t=0
dt
Dalla seconda equazione abbiamo
α=0
(32)
e sostituendo nella prima otteniamo
z(t = 0) = l0 −
mg
+ A cos
| {z 0} = l0
k
=−1
mg
⇒ A=
k
(33)
Sostituendo nell’Eq.(31) i valori (33) e (34) trovati per le costanti, otteniamo la soluzione
dell’equazione (21) che soddisfa le particolari condizioni iniziali (22)
r
mg mg
k
+
cos(ωt)
(34)
z(t) = l0 −
ω=
k
k
m
La velocità del punto materiale è data da
dz
mg
v(t) =
= −ω
sin(ωt)
dt
k
r
ω=
k
m
(35)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
8
Avendo trovato la legge oraria del punto materiale possiamo ora rispondere ai vari quesiti del problema:
1. La massima distanza percorsa corrisponde all’altezza minima raggiunta dal punto materiale; denotiamo con z ∗ tale altezza (ancora ignota) e con t∗ il tempo impiegato a raggiungerla (anch’esso
ignoto). Dopo che il punto è sceso e ha compresso la molla fino all’altezza z ∗ , la molla si estende
e il punto materiale viene proiettato verso l’alto. All’altezza z ∗ la velocità si annulla e dunque il
punto z ∗ è determinato dalla condizione
v(t∗ ) = 0
(36)
Sostituendo nell’espressione (36) otteniamo
0 = v(t∗ ) = −
mg
sin ωt∗
k
(37)
che ha come soluzioni
i) t
= 0 (corrisponde all’istante iniziale, in cui infatti la vel. è nulla)
(38)
ii) ωt∗ = π → t∗ =
π
ω
(corrisponde all’altezza minima)
Pertanto l’altezza minima vale
z ∗ = z(t∗ ) = l0 −
mg mg
+
k
k
cos(ωt∗ )
| {z }
=−1,vedi
= l0 −
=
Eq.(39)
2mg
k
(39)
E dunque la deviazione massima dalla posizione iniziale di equilibrio vale
∆z = −
2mg
k
(40)
Sostituendo i valori numerici otteniamo
2mg
2T
=−
=
k
k
2 · 4.9 N
−
=
N
70 m
= −0.14 m
∆z = −
(41)
2. Il punto materiale parte inizialmente con velocità nulla, e poi si ferma istantanemente all’altezza
z ∗ trovata al punto precedente. Quindi durante la discesa la velocità cresce fino ad un certo
valore massimo, per poi decrescere fino ad annullarsi nuovamente. Denotiamo con t̄ l’istante
in cui la velocità è massima. Dall’espressione (36) per la velocità possiamo vedere l’istante t̄ è
determinato dalla condizione
dv
=0
(42)
dt
ossia
mg 2
π
−
ω cos(ω t̄) = 0
⇒ ω t̄ =
(43)
k
2
Denotando con z̄ la posizione corrispondente al massimo della velocità, abbiamo
mg mg
z̄ = z(t̄) = l0 −
+
cos ω t̄ =
k
k | {z }
=0
mg
= l0 −
k
(44)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I
9
che devia dalla posizione iniziale di equilibrio di una quantità
∆z = −
mg
k
(45)
Sostituendo i valori numerici
∆z = −
mg
4.9 N
=− N =
k
70 m
= −0.07 m
(46)
3. Il valore della velocità massima è (per definizione di istante t̄)
vmax = v(t̄) =
mgω
= −
sin ω t̄ =
k
mgω
= −
=
k
q
k
[uso ω = m
]
r
mg k
=
= −
k
m
r
mg 2
= −
=
k
[uso mg = T ]
r
Tg
= −
k
(47)
s
m 4.9 N
=
N
s2 70 m
r
9.81 · 4.9 m 2
= −
=
70
s
m
= −0.83
s
vmax = − 9.81
(48)
Fabrizio Dolcini (http://staff.polito.it/fabrizio.dolcini/)
Dipartimento di Scienza Applicata e Tecnologia, Politecnico di Torino - Esercitazioni di Fisica I