Verifica sui Principi della Dinamica
Classe 3E (recupero)- 4 dicembre 2014
Durata: 55 minuti. Soglia sufficienza: 60 pt. Punteggio massimo: 100 pt.
Es. 1 Considera due corpi di masse m1 = 150.0 kg e m2 = 50.0 kg appoggiati ad un piano orizzontale scabro
(µd = 0.100), a contatto fra loro e inizialmente in quiete. Il primo corpo è soggetto ad una forza di intensità
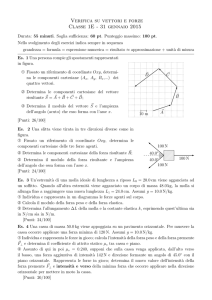
F1 = 2400 N e il secondo a una forza F2 = 1200 N dirette come in figura.
F~1
F~2
m1
m2
À Stabilita la direzione di movimento del sistema, traccia i due diagrammi del corpo
libero includendo tutte le forze agenti sui singoli corpi.
Á Determina l’intensità delle due reazioni vincolari e delle forze di attrito.
 In un opportuno riferimento scrivi le equazioni del secondo principio delle dinamica relative a ciascun corpo e risolvile determinando l’accelerazione del sistema e
l’intensità della forza di contatto .
[PUNTI 24/100]
Es. 2 Considera un corpo di massa 100 kg, inizialmente in quiete, appoggiato ad un piano inclinato di altezza
h = 5.00 m, privo di attrito e formante un angolo θ = 30.0◦ con il piano orizzontale.
À Traccia il diagramma del corpo libero del corpo riportando le componenti della forza
peso rispettivamente parallela (Pk ) e perpendicolare (P⊥ ) al piano inclinato.
Á Determina le intensità della reazione vincolare R e della forza risultante agente sul
corpo.
 Determina in un opportuno riferimento l’accelerazione del corpo e il tempo impiegato
a discendere il piano.
h
θ
[PUNTI 26/100]
Es. 3 Considera una cassa di massa m appoggiata su una bilancia all’interno di un ascensore, come rappresentato in
figura. Quando l’ascensore sale con accelerazione di modulo as = 2.00 m/s2 la bilancia segna 24.0 kg, essendo 240 N
la reazione normale che il piatto della bilancia esercita sulla cassa. Nella fase di discesa la bilancia segna invece
16.0 kg.
Fase 1
Fase 2
~as
~ad
m
m
À In entrambe le situazioni proposte: traccia il diagramma del
corpo libero della cassa e scrivi le equazioni del secondo principio
della dinamica utilizzando un medesimo riferimento.
Á Determina la massa m della cassa e l’intensità dell’accelerazione
ad nella fase di discesa.
[PUNTI 24/100]
Es. 4 Una curva sopraelevata di un’autostrada ha raggio R pari a 400 m e angolo di sopraelevazione θ, ed è progettata
per una velocità di 90.0 km/h.
R
~g
θ
[PUNTI 26/100]
À Qual è il giusto angolo di sopraelevazione θ del piano stradale affinché, in assenza
di attrito, un veicolo di massa m = 1000 kg possa percorrere la curva senza perdere il
controllo?
Á Se la curva non fosse sopraelevata, cioè θ = 0◦ , e avesse medesimo raggio, e il
coefficiente di attrito statico fra strada e battistrada fosse µs = 0.500, quale sarebbe
la massima velocità con cui il veicolo potrebbe affrontare la curva senza perdere il
controllo?
Si assuma in tutti gli esercizi g = 10.0 ms−2 .