Chimica Fisica - Chimica e Tecnologia Farmaceutiche
Lezione n. 11
−
−
−
−
−
Diagrammi p-x e TT-x
Distillazione
Azeotropi
Liquidi parzialmente miscibili
Grandezze d’eccesso
02/03/2008
Antonino Polimeno
1
Antonino Polimeno
2
Diagrammi p, T, x (1)
- Un sistema bifasico bicomponente ha
varianza due
- Possiamo ottenere una relazione tra T, p e x1
- Possiamo razionalizzare il comportamento dei
sistemi bifasici bicomponenti mediante
diagrammi p-composizione e Tcomposizione
Antonino Polimeno
3
Diagrammi p-composizione (1)
- Per una soluzione ideale, dalla legge di Raoult
p = p + ( p − p ) x1
*
2
y1
*
1
=
p =
*
2
*
1 1
*
1
xp
*
*
p2 + ( p − p2 ) x1
*
1
*
2
*
2
p p
*
*
p1 + ( p − p1 ) y1
Antonino Polimeno
4
*
1
p
*
2
p
Antonino Polimeno
fissato
5
Diagrammi p-composizione (2)
- Fissiamo la temperatura → diagramma p-x
- La retta in diagonale rappresenta la tensione di vapore
totale di una soluzione di composizione data (ascissa come
x1); i punti sopra la retta sono fasi liquide, poichè la
pressione è superiore alla tensione di vapore.
- La curva rappresenta la tensione di vapore totale di una
vapore di composizione data (ascissa come y1); i punti sotto
la curva sono fasi vapore, poichè la pressione è inferiore
alla tensione di vapore.
- La zone compresa tra la retta e la curva rappresenta la
coesistenza delle due fasi: l'ascissa in questo caso la
frazione molare totale del componente 1 nel sistema, che
indichiamo con z1.
- La zona superiore, avendo fissato la temperatura, è a
varianza 2;
- quella intermedia è a varianza 1
- quella inferiore è a varianza 2.
Antonino Polimeno
6
Antonino Polimeno
7
Regola della leva
- Se indichiamo con nliq e nvap il numero di moli totali di
soluzione e vapore, possiamo scrivere
nz1 ≡ ( nliq + nvap ) z1 = nliq x1 + nvap y1
nliq ( x1 − z1 ) = nvap ( z1 − y1 ), lliq = x1 − z1 , lvap = z1 − y1
nliq lliq = nvaplvap
Antonino Polimeno
8
Distillazione (1)
- Il processo di distillazione si
basa
sull'idea
che
il
componente più volatile di una
soluzione
è presente in
proporzioni maggiori nel vapore
che nella soluzione
- Condensando il vapore sottratto
al sistema si ottiene dunque
una
soluzione
a
diversa
composizione, che è via via,
ripetendo la procedura, più
ricco nel componente più
volatile.
Antonino Polimeno
9
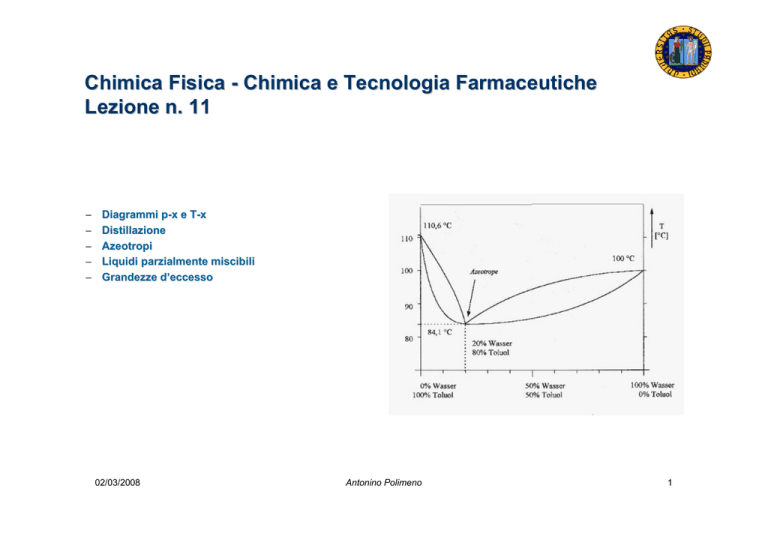
Distillazione (2)
-
Per l'interpretazione di questo tipo di processi si possono impiegare i
diagrammi T-x, a pressione costante (di solito 1 atm)
La zona del liquido è sotto la curva inferiore, che indica la temperatura
di ebollizione
La curva superiore indica la composizione di un vapore in equilibrio con
un liquido ad una data temperatura
Antonino Polimeno
10
Antonino Polimeno
11
Antonino Polimeno
12
Liquidi parzialmente miscibili (1)
- Due liquidi parzialmente miscibili possono essere
studiati in presenza e in assenza di fase vapore, dal
punto di vista della regola delle fasi.
- A basse frazioni molari del primo componente i due
componenti si mescolano in presenza di fase vapore
- Nella zona centrale si formano due fasi liquide a
composizione costante (una più ricca in un
componente e l'altra nell'altro) in equilibrio con una
fase vapore;
- Segue poi una zona in cui la fase liquida diviene
nuovamente una sola.
- Nella zona centrale, a causa della regola delle fasi, il
sistema è monovariante (2 componenti e 3 fasi), quindi
se si fissa la pressione totale le tensioni di vapore parziali
dei due componenti restano le stesse.
Antonino Polimeno
13
Antonino Polimeno
14
Liquidi parzialmente miscibili (2)
- Diagrammi temperatura-composizione per soluzioni
binarie mono o bifasiche di liquidi parzialmente miscibili, in
assenza di fase vapore (cioè sotto la temperatura di
ebollizione)
- Nelle regioni di composizione dove i due liquidi non si
mescolano, sono presenti due fasi (cioè due soluzioni
liquide a diversa composizione) e quindi la varianza è
2; fissata la pressione, per ogni temperatura la
composizione delle due fasi è determinata.
- Se i due liquidi si mescolano completamente, si ha una
sola fase, e quindi la varianza è 3: a pressione fissata,
sia la temperatura che la composizione della fase
possono essere variate liberamente.
Antonino Polimeno
15
Liquidi parzialmente miscibili (3)
-
Diagramma temperatura-composizione per due componenti liquidi 1 e 2 in funzione di z2 (frazione molare totale di 2),
a pressione fissata.
Antonino Polimeno
16
Liquidi parzialmente miscibili (4)
-
Per una data temperatura, inferiore alla temperatura critica superiore Tc a basse concentrazioni del
liquido 2 si ha un'unica fase, ricca in 1;
Al crescere di z2 si giunge alla formazione di due fasi, una ricca in 1 (e in maggior quantità), ed una
ricca in 2 (in tracce).
Le due curve indicano la composizione delle due fasi ad ogni temperatura, e l'abbondanza relativa
delle due fasi ad una temperatura è data dalla regola della leva
nsol. di 2 in 1lsol. di 2 in 1 = nsol. di 1 in 2lsol. di 1 in 2
Antonino Polimeno
17
Liquidi parzialmente miscibili (5)
- Al crescere di z2, la composizione delle due fasi non
cambia, perchè per la regola delle fasi in presenza di
due fasi la varianza è due (T e p sono fissate)
- aumenta però l'abbondanza della seconda soluzione,
ricca in 2;
- Infine la quantità di 2 aggiunta è tale da portare alla
scomparsa della soluzione ricca in 1 e alla presenza di
un'unica soluzione ricca in 2.
- Sopra la temperatura critica, i due liquidi sono
completamente miscibili, e quindi la varianza è tre:
anche a temperatura e pressione fissata, la
composizione dell'unica soluzione può cambiare.
- Temperatura critica inferiore /superiore → solo
sotto/sopra Tc i liquidi sono completamente miscibili
Antonino Polimeno
18
Soluzioni solido-liquido (1)
Es. Soluzione di due componenti A e B quasi immiscibili in forma solida,
e completamente mescolabili in Antonino
forma
liquida
Polimeno
19
Soluzioni solido-liquido (2)
- A temperatura elevata il sistema si presenta come una
sola fase liquida, bicomponente (quindi a varianza 3: a
pressione fissata e temperatura fissata la composizione
può variare).
- Scendendo con la temperatura, il sistema entra in una
regione in cui sono presenti due fasi, con una soluzione e
uno dei due componenti in forma solida, per esempio A
- La soluzione ha una composizione indicata dal punto
della curva relativa alla composizione totale data e
l'ammontare relativo di liquido e solido è dato dalla
regola della leva; continuando a scendere con la
temperatura si giunge alla separazione dei due solidi.
- Il punto a temperatura più bassa in cui coesistono la
soluzione ed un solido si dice punto eutettico: una
soluzione al punto autentico congela senza prima
depositare in forma solida uno suoi componenti.
Antonino Polimeno
20
Nomenclatura
-
Punto eutettico - temperatura minima di un diagramma
T-x a cui il liquido coesiste con il solido
Liquidus – curva sopra la quale non esiste una fase
solida.
Solidus – curva sotto la quale non esiste una fase
liquida.
Antonino Polimeno
21
Sistemi multi-componente
- I sistemi tri-componenti (A+B+C) sono visualizzabili sotto
forma di diagrammi ternari
- Ogni vertice corrisponde ad una sostanza pura, es. A
- Il lato opposto corrisponde ad una miscela delle altre due
sostanze B+C
- In un punto dato La frazione molare di A si ottiene dalla
‘distanza’ rispetto al lato opposto
Antonino Polimeno
22
Grandezze di eccesso (1)
-
-
Le proprietà termodinamiche delle soluzioni reali vengono espresse
mediante le grandezze di eccesso che rappresentano la differenza
tra l'energia libera, l'entalpia, l'entropia di mescolamento etc. della
soluzione e la corrispondente funzione di mescolamento della
soluzione ideale alla stessa composizione, temperatura e pressione.
Per una generica grandezza estensiva X
X = ∆ mix X − ∆
E
Antonino Polimeno
ideale
mix
X
23
Grandezze di eccesso (2)
- L'entità delle grandezze di eccesso rappresenta il grado di
deviazione dall'idealità di una soluzione
- La definizione delle grandezze di eccesso in termini di
opportune funzioni dei parametri di composizione,
temperatura, pressione, dedotte a partire da modelli
molecolari od inferite da osservazioni sperimentali,
permettono di determinare modelli specifici delle soluzioni
reali.
- Uno dei modelli più utili è quello delle soluzioni regolari,
per le quali si definiscono deviazioni dall'idealità
dell'entalpia di eccesso, mentre si assume che l'entropia
di eccesso sia nulla.
H E = nβ RTx1 x2
SE = 0
Antonino Polimeno
24