Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
Creato il 10/12/2002 9.46
stampato il 17/12/2002 10.44
Momento angolare
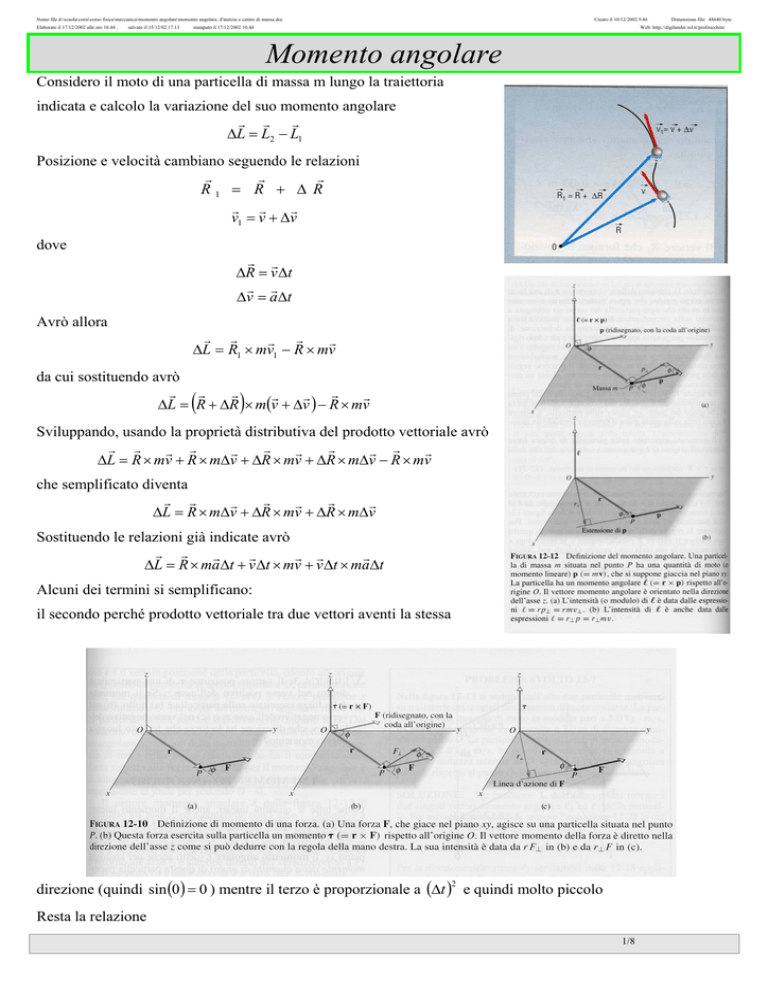
Considero il moto di una particella di massa m lungo la traiettoria
indicata e calcolo la variazione del suo momento angolare
r r r
∆L = L2 − L1
Posizione e velocità cambiano seguendo le relazioni
r
r
r
R1 = R + ∆ R
r
r r
v1 = v + ∆v
dove
r r
∆R = v ∆t
r r
∆v = a∆t
Avrò allora
r r
r r
r
∆L = R1 × mv1 − R × mv
da cui sostituendo avrò
r r
r
r
r r
r
∆L = R + ∆R × m(v + ∆v ) − R × mv
(
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
)
Sviluppando, usando la proprietà distributiva del prodotto vettoriale avrò
r r
r
r
r r
r
r
r r
r
∆L = R × mv + R × m∆v + ∆R × mv + ∆R × m∆v − R × mv
che semplificato diventa
r r
r
r
r
r
r
∆L = R × m∆v + ∆R × mv + ∆R × m∆v
Sostituendo le relazioni già indicate avrò
r r
r
r
r r
r
∆L = R × ma ∆t + v ∆t × mv + v ∆t × ma∆t
Alcuni dei termini si semplificano:
il secondo perché prodotto vettoriale tra due vettori aventi la stessa
direzione (quindi sin (0 ) = 0 ) mentre il terzo è proporzionale a (∆t ) e quindi molto piccolo
2
Resta la relazione
1/8
Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
stampato il 17/12/2002 10.44
Creato il 10/12/2002 9.46
(
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
)
r r r
∆L = R × F ∆t
r r r
dove ponendo M = R × F (momento di una forza)
avrò infine
r
r
M∆t = ∆L
(“impulso” per le rotazioni)
o anche
r
r ∆L
M=
∆t
(secondo principio della dinamica per le rotazioni)
Il parallelismo con la dinamica lineare si evidenzia meglio ponendo a confronto le relazioni:
dinamica lineare
r ∆pr
r
F=
= ma
∆t
r
r
F∆t = m∆v
Dinamica delle rotazioni
r
r ∆L
M=
∆t
r
r
M∆t = ∆L
r
r
F →M
r
r
p→L
Con l’introduzione del momento d’inerzia si evidenzierà ancor meglio il parallelismo fra dinamica lineare e
delle rotazioni.
Momento d’inerzia
Considero un sistema costituito da 3
corpi rigidamente posti a distanze
note dal centro di rotazione O.
Le tre masse si muovono ruotando a
velocità angolare ω .
Le velocità lineari saranno quindi
v1 = ωR1
v2 = ωR2
v = ωR
3
3
r
r
r
Ancora meglio dovrei esprimere vettorialmente le velocità come v i = ω × R i
Scrivo l’energia cinetica del sistema:
EC =
1 3
1 3
2
2
mi vi = ∑ miω 2 Ri
∑
2 i =1
2 i =1
raccogliendo avrò
2/8
Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
Creato il 10/12/2002 9.46
stampato il 17/12/2002 10.44
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
1 3
2
EC = ∑ mi Ri ω 2
2 i =1
Scrivo il momneto angolare del sistema:
r 3 r
r
L = ∑ Ri ×m i vi
i =1
(
r 3 r
r r
L = ∑ Ri × mi ω × Ri
)
i =1
da cui
r 3
r
L = ∑ mi Ri 2ω da cui infine
i =1
r 3
r
L = ∑ mi Ri 2 ω
i =1
Nelle due relazioni citate ricorre la quantità
r2
m
R
∑ i i che dipende dalle masse e dalla loro distribuzione
3
i =1
3
spaziale; questa quantità è detta Momento d’inerzia I = ∑ mi Ri 2 e con questa notazione si ha
i =1
1 2
Iω
2
r
r
L = Iω
EC =
Rivediamo il parallelismo fra dinamica lineare e dinamica delle rotazioni:
dinamica lineare
r
r ∆pr
r
∆v
F=
= ma = m
∆t
∆t
r
r
F∆t = m∆v
Dinamica delle rotazioni
r
r
r ∆L
∆ω
M=
=I
∆t
∆t
r
r
r
M∆t = ∆L = I∆ω
1
EC = mv 2
2
r
r
p = mv
1 2
Iω
2
r
r
L = Iω
EC =
r
r
F →M
r
r
p→L
m→I
r
r
v →ω
r
r
∆v
∆ω
→
∆t
∆t
3/8
Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
Creato il 10/12/2002 9.46
stampato il 17/12/2002 10.44
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Centro di massa
Considero la quantità di moto di un sistema di punti materiali espressa rispetto ad un sistema di riferimento oxy
r
r
P = ∑ mi vi
i
Considero poi la quantità di moto dello stesso sistema di punti materiali ma visto da un sisitema di riferimento
r
o′x′y ′ in moto relativo al primo a velocità V e tale per cui ogni singolo punto materiale avrà velocità
r r′ r
v i = vi + V
r
r′ r
Sostituendo nella relazione iniziale avrò P = ∑ mi vi + V da cui avrò
i
r
r
r′
P = ∑ mi vi + ∑ miV
i
i
r
r′
e ponendo P′ = ∑ mi vi potrò scrivere
i
r r r
P = P′ + V ∑ mi
i
r
Il valore di P′ dipende dalla scelta del sistema di riferimento o′x′y ′ e quindi con una scelta opportuna potrò
r
avere P ′ = 0
r
La domanda è allora quanto vale la velocità V per cui il sistema di riferimento accentato rappresenti il sistema
r
a quantità di moto nulla P ′ = 0
Avrò
r r
P = V ∑ mi
i
da cui
r
V=
r
P
=
∑ mi
i
r
∑m v
∑m
i i
i
i
i
La relazione appena trovata individua un “ambiente” particolare in cui studiare il moto complessivo del sistema
r
dato che in esso il sistema di punti nel loro insieme appare in quiete (perché P ′ = 0 ).
Da questa relazione, moltiplicando per il tempo si avrà
r
mi vi
r
r ∑
X cm = Vt = i
t=
∑ mi
r
r
∑m v t ∑m x
=
∑m
∑m
i i
i
i i
i
i
i
i
i
i
r
La posizione del punto X cm in ogni istante t è determinato dall’uguaglianza
r
m
x
∑
i
i
r
X cm = i
∑ mi
i
4/8
Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
Creato il 10/12/2002 9.46
stampato il 17/12/2002 10.44
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Questo punto è detto centro di massa e rispetto ad esso il sistema di punti ha quantità di moto nulla.
Nello studio delle proprietà meccaniche di un sistema isolato di punti materiali è naturale servirsi di un sistema
di riferimento in cui il centro di massa persevera in quiete.
L’energia di un sistema meccanico perseverante in quiete è detta energia interna e l’osservazione dal centro di
massa consente proprio di valutare questa energia interna senza preoccuparsi del moto traslatorio del sistema
nel suop complesso (dato che questo è “contenuto” nel moto del sistema di riferimento del centro di massa )
r
mi vi
r ∑
Partendo dalla precedente V = i
si può anche fare la seguente considerazione:
∑ mi
i
r
r
∆xi
r ∑ mi
∆
m
x
∑
i
i
r
r ∆X
∆t
da cui semplificando ∆X = i
= i
V=
∆t
∑ mi
∑ mi
i
i
Avrò poi
r r
r
∆X = X f − X i
r
r
∑ m (x − x )
da cui avrò separando le grandezze riferite agli istanti iniziale e finale avrò
=
∑m
i
if
ii
i
i
i
r
r
mi xii
mi xif
∑
r ∑
r
Xi − i
=Xf − i
m
∑ i
∑ mi
i
i
Questo implica che la grandezza
r
mi xi
r ∑
r
X− i
si mantega costante, ovvero X cm =
∑ mi
i
r
∑m x
∑m
i i
i
r
+c
i
i
r
r
ma c è solo una traslazione e quindi posso supporre c = 0 giungendo anche da questa strada alla relazione già
trovata per il centro di massa
r
X cm =
r
∑m x
∑m
i i
i
i
i
Momento d’inerzia di corpi rigidi comuni
Abbiamo detto che il momento d’inerzia è definito dalla relazione
n
I = ∑ mi Ri 2
i =1
ma quando i corpi sono continui (cioè corpi costituiti da materia non riconducibile a somma di punti materiali)
è necessario passare dalla sommatoria all’integrale
I = ∫ r 2 dm
5/8
Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
Creato il 10/12/2002 9.46
stampato il 17/12/2002 10.44
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Il calcolo porta ai seguenti risultati riassunti in tabella:
Da notare che quasi tutti i momenti d’inerzia presentati (tranne il caso f) ruotano per assi passanti per il centro
di massa.
teorema di Steiner
Quando si conosce il momento d’inerzia di un corpo rigido rispetto
ad un asse passante per il centro di massa e si desidera conoscere il
momento d’inerzia per un asse ad esso parallelo, posto a distanza d
dal centro di massa si applica il teorema di Steiner:
Considero due sistemi di riferimento:
1. o′x′y ′ la cui origine coincide con il centro di massa del corpo
2. oxy con origine qualsiasi
r
r r r
I punti del corpo sono individuati dai vettori ri = ri′ + d dove d
individua la posizione relativa delle origini dei sistemi.
6/8
Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
Creato il 10/12/2002 9.46
stampato il 17/12/2002 10.44
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
Dimostreremo il teorema partendo dalla relazione
(
r r
2
I = ∑ m i ri = ∑ m i ri ′+ d
i
)
2
i
Ricordando le regole sul prodotto scalare
(
r r
′2
I = ∑ m i ri + ∑ m i d 2 + 2∑ mi r ′i ⋅d
i
i
)
i
r
r
′2
I = ∑ m i ri +d 2 ∑ m i + 2d ⋅ ∑ mi r ′i
i
i
i
ma l’ultimo termine è legato alla posizione del centro di massa
r′
∑m r
i
i
r
= Mr ′CM che nel sistema di riferimento
i
r
r
r′
′2
scelto è l’origine (r ′CM = 0 ) e quindi si ha I = ∑ m i ri + d 2 ∑ m i + 2d ⋅ ∑ mi r i da cui segue infine il teorema
i
i
i
1
424
3
1
23
1
4
24
3
I CM
0
M
di Steiner
I = I CM + Md 2
Lo stesso calcolo si potrebbe sviluppare più in generale e più correttamente utilizzando gli integrali
r r2
I = ∫ r 2 dm = ∫ r ′ + d dm
(
(
)
)
r r
r r
I = ∫ r ′ 2 dm + ∫ d 2 dm + 2∫ r ′ ⋅ d dm = ∫ r ′ 2 dm + d 2 ∫ dm + 2d ⋅ ∫ r ′dm
ma l’ultimo termine nel sistema del centro di massa è nullo, coincidendo con l’origine e quindi resta
I = ∫ r ′ 2 dm + d 2 ∫ dm = I CM + Md 2
Teorema di Köening
Come nel caso precedente considero i due sistemi, o′x′y ′ d’origine coincidente con il centro di massa del corpo
studiato e oxy d’origine qualsiasi.
La relazione tra le velocità sarà
Considero poi l’energia cinetica del corpo vista dal sistema non accentato.
EC =
r r
1
mi (vi ⋅ vi )
∑
2 i
r r′ r
sostituendo le velocità con vi = vi + V come in precedenza si avrà
EC =
1
r′ r 2
mi vi + V
∑
2 i
che sviluppato darà
EC =
r′ r 1
1
2
′2 1
m
v
+
m
v
miV
∑
∑
∑
i i
i i ⋅V +
2 i
2 i
2 i
da cui si avrà
7/8
Nome file d:\scuola\corsi\corso fisica\meccanica\momento angolare\momento angolare, d'inerzia e centro di massa.doc
Elaborato il 17/12/2002 alle ore 10.44 ,
salvato il 15/12/02 17.13
Creato il 10/12/2002 9.46
stampato il 17/12/2002 10.44
EC =
Dimensione file: 48640 byte
Web: http://digilander.iol.it/profzucchini
r′ 1
1
′2 1 r
m
v
+ V ⋅ ∑ mi vi + V 2 ∑ mi
∑
i i
24
i
i
i
1
243 2 1
4
24
3 2 1
23
EC ′
0
M
da cui segue infine il Teorema di Köening
1
′
EC = EC + MV 2
2
L’energia cinetica di un sistema in moto è uguale all’energia cinetica che esso possiede rispetto ad un
riferimento baaricentrico aumentata dell’energia cinetica che avrebbe un punto il quale si muovesse con
velocità del baricentro e nel quale fosse concentrata tutta la massa del sistema.
Nel caso il corpo sia rigido e in rotazione attorno ad un asse passante per il barigentro sappiamo già che
′ 1
l’energia cinetica di rotazione sarà EC = Iω 2
2
E quindi per il teorema di Köening avremo
EC =
1 2 1
Iω + MV 2
2
2
come espressione dell’energia cinetica di rototraslazione.
EC =
1 2 1
Iω + MV 2
2
2 23
123 1
rotazione
traslazione
8/8












