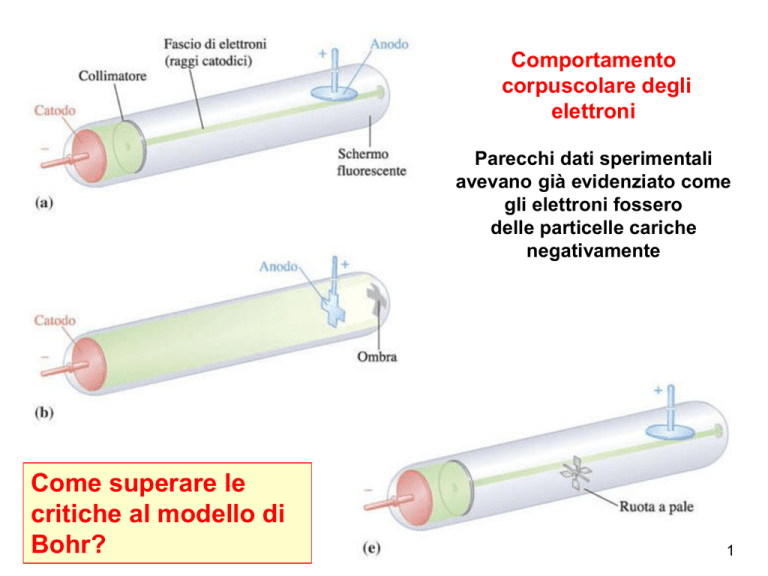
Comportamento
corpuscolare degli
elettroni
Parecchi dati sperimentali
avevano già evidenziato come
gli elettroni fossero
delle particelle cariche
negativamente
Come superare le
critiche al modello di
Bohr?
11
Si potrebbe considerare
ondulatorio degli elettroni?
un
comportamento
De Broglie affermò che le particelle elementari possono
presentare, in analogia al comportamento della radiazione
elettromagnetica, proprietà tipiche delle onde.
Se si parte dalla relazione di Planck: E h
e si considera che
secondo Einstein
della luce
c
E mc2
Eh
c
dove m è la massa e c la velocità
il momento o quantità di moto p di una particella è
p mv
p mc E pc
si può scrivere
pc h
c
p
h
2
m (g)
v (cm/s)
(Å)
elettrone a 300 K
9.1·10-28
1.2·107
61.0
elettrone a 1 V
9.1·10-28
5.9·107
12.0
elettrone a 100 V
9.1·10-28
5.9·108
1.20
atomo di He 300 K
6.6·10-24
1.4·105
0.71
atomo di Xe 300 K
2.2·10-22
2.4·104
0.12
1
1
6.6·10-19
Particella
particella di 1 g
alla v = 1 cm/s
h
6.626×10-27 erg s
(CGS)
6.626×10-34 J s
(SI)
--------1 Å = 10-8 cm
3
Ecco perché un fascio di elettroni subisce diffrazione,
in perfetta analogia ad un fascio di raggi X.
Dualismo onda-particella
4
Cosa comporta considerare l’elettrone
come un’onda?
Quando si fa vibrare una corda di
chitarra, che è una vibrazione che
avviene tra due vincoli, non tutte le
vibrazioni audio sono possibili, ma
solo quelle che hanno una relazione
con la lunghezza della corda. Se vario
la lunghezza della corda cambia “la
nota”. La vibrazione totale che
avviene è rappresentata dall’inviluppo
delle vibrazioni permesse (corda di
chitarra → suono) e si genera uno
spettro audio, cioè la nota che il
nostro orecchio sente è il suono
prodotto
dalla
vibrazione
fondamentale più tutte le vibrazioni
permesse.
Quindi abbiamo un
esempio di sistema quantizzato
macroscopico. Quale la condizione?
Che la corda di chitarra sia ben ferma
tra i due vincoli.
5
Questo significa che anche per particelle elementari, come
l’elettrone, che si muovono a velocità elevate prossime a quella
della luce è possibile considerare un’onda associata al loro moto.
Qual è la condizione? Che esse siano sottoposte ad un vincolo,
come nella corda di chitarra ed il vincolo per gli elettroni è che essi
sono costretti a muoversi dentro il campo elettrico creato dal
nucleo. Infatti, se diamo parecchia energia, tale da liberarli
dall’influenza del nucleo, essi si comportano da particelle.
Quindi quando l’elettrone si trova all’interno di un atomo emergono
le sue proprietà ondulatorie, quando esso si trova fuori si
comporta come una particella normale, ed anche per esso
possiamo parlare di doppia natura (corpuscolare ed ondulatoria).
Quando consideriamo la sua natura ondulatoria gli spettri a righe
degli atomi sono facilmente giustificabili (e non abbiamo bisogno
di condizioni aggiuntive) così come accadeva per lo spettro audio
della corda di chitarra.
6
Natura duale onda-corpuscolo della materia e della luce
= h /mv
L'elettrone ha una massa pari a 9,1095×10-31 Kg
7
Nella natura dualistica delle
particelle elementari vi è insito
un
concetto,
quello
di
conoscenza probabilistica non
assoluta.
Tutto
ciò
viene
espresso sinteticamente dal
Principio di indeterminazione di
Heisenberg:
Dx Dp h/4p
8
L’equazione precedente che può anche essere scritta:
Dx Dv
2m
mostra chiaramente :
• per particelle molto pesanti, ħ/2m è piccolo, e quindi il
prodotto degli errori Dx e Dv è piccolo, cioè sia la velocità
che la posizione possono essere determinati con
sufficiente accuratezza.
• se m è molto piccolo, come nel caso delle particelle
elementari, ħ/2m è grande, quindi anche il prodotto degli
errori Dx e Dv è grande, cioè la posizione e la velocità non
potranno più essere contemporaneamente determinate
con sufficiente accuratezza.
9
Definire le traiettorie degli elettroni intorno ad un
nucleo di un atomo è impossibile, non per la
pochezza dei nostri mezzi di osservazione, ma
concettualmente impossibile per la natura stessa
della materia.
Un’orbita di un elettrone non è una entità
osservabile e quindi non ha senso tentare di
definirla
10
L'oggetto di cui si parla perde la sua
unicità e le sue proprietà sostanziali.
La particella elementare non ha né
dimensioni, né forma determinate.
11
• La particella si può creare od annullare. Il principio di
conservazione della massa che vale nelle reazioni chimiche,
dove entrano in gioco gli atomi (individui chimici) non vale più.
Così ad esempio per impatto di un elettrone con un positrone
(elettrone con carica positiva) si ha il fenomeno
dell'annichilazione con produzione di energia sotto forma di
radiazione elettromagnetica (si ottengono due fotoni da 0.51
MeV) e dall'interazione dei radiazione elettromagnetica con la
materia (se il fotone incidente ha energia superiore alla soglia di
1.02 MeV) si ha scomparsa della radiazione stessa con la
creazione di due particelle elementari (una coppia elettrone, e-,
positrone, e+).
• Le particelle elementari vengono studiate tramite il loro
interagire. Non esiste altro modo per ricavare informazioni sulle
proprietà delle particelle elementari se non osservando cosa
accade nell'interazione con le altre particelle.
12
Ma se dobbiamo trattare l’elettrone come un’onda occorre
una funzione (che dobbiamo trovare) che ne descriva
esaurientemente queste proprietà.
Nell’atomo l’energia associata ad un elettrone (trascurando i moti
nucleari) è data dalla somma dell’energia cinetica e dell’energia
potenziale:
1
e2
2
E mv
2
r
E T V
ma p = mv, ovvero p2 = m2v2, quindi:
1
p2
2
mv
2
2m
p 2 e2
E
2m r
Il passaggio dalla meccanica classica alla meccanica ondulatoria fa si
che mentre nella meccanica classica il momento era una quantità
vettoriale, caratterizzata da un modulo ed una direzione, nella meccanica
ondulatoria diventa un operatore, cioè un oggetto matematico che mi
dice quale operazione devo fare su una certa funzione:
p
h
d
2p i dx
p
2
h2 d 2
4p 2 dx 2
13
Gli operatori in matematica
Come suggerisce il nome stesso, un operatore matematico compie una
operazione matematica sulla funzione in questione. La derivata è un tipo
di operazione matematica.
Per esempio:
d
deriva una variabile rispetto ad x.
dx
Sia
y
la
variabile
su
cui
y = 8x. Si calcoli la derivata dy/dx:
dy
dx
agisce
il
d (8 x)
8
differenziale,
con
dx
L’operatore Hamiltoniano, H, è un operatore differenziale complesso ed è
uguale a:
h 2 2
2
2
V ( x, y , z )
8p 2 m x 2 y 2 z 2
termine dell’energia
derivate parziali
potenziale
La natura complessa di H deriva dalla necessità di descrivere la posizione
dell’elettrone in uno spazio cartesiano a tre dimensioni
14
Detta la funzione d’onda, cioè la funzione che contiene tutte le
informazioni riguardanti l’elettrone avremo:
h2 d 2 e2
E
8p 2 m dx 2 r
Questa equazione vale solo per il moto nella dimensione x, per
considerarla nello spazio dovremo aggiungere gli altri termini (cioè y e
z). Cioè p è diventato una istruzione che deve operare sulla funzione .
h 2 2 2 2 e 2
E
2
2
2
2
8p m x
y
z r
Η E
Equazione di Schrödinger
Questa è un’equazione differenziale che ammette infinite soluzioni! Ma
quali sono quelle fisicamente accettabili? In altre parole, le funzioni
d’onda, soluzioni dell’equazione precedente, hanno tutte un
significato fisico?
15
Per definire delle soluzioni valide da un punto di vista fisico:
• Le funzioni devono essere finite, continue ed ad un solo valore,
come pure le loro derivate in ogni punto dello spazio.
• La probabilità (2 rappresenta proprio la probabilità di trovare
l’elettrone ed è ciò che ha significato fisico per il principo di
indeterminazione di Heisemberg) deve corrispondere al 100%
2 dv 1
Quindi quello che ha significato fisico è il quadrato della
funzione d’onda, poiché essa è in relazione alla probabilità di
trovare l’elettrone.
La funzioni d’onda
Senza entrare nel merito della soluzione dell’equazione di
Schrödinger, possiamo affermare che le funzioni d’onda
possono essere classificate in base a tre numeri quantici
16
• n, numero quantico principale
n,l,ml
E’ in relazione alla quantizzazione dell’energia (cioè l’energia
dei livelli dipende da esso). Può assumere tutti i valori interi da
1 a infinito.
n=1, 2, 3 , 4, 5,…….,
• l, numero quantico angolare
esso quantizza il momento angolare dell’elettrone e può
assumere tutti i valori interi da 0 a n-1. l = 0, 1, 2, 3,…..,n-1
• m, numero quantico magnetico
quantizza il momento magnetico dell’elettrone (una particella
carica che si muove genera una corrente elettrica che avrà un
campo magnetico associato). Può assumere tutti i valori che
vanno da –l a +l, incluso lo zero. m = -l,.., -2, -1, 0, 1, 2,.., +l
17
L’equazione di Schrodinger ammette soluzioni accettabili, cioè
permette di definire delle funzioni d’onda fisicamente appropriate a
descrivere lo stato di un elettrone in un atomo d’idrogeno, solo per
determinati valori di energia (autovalori) caratterizzati da un numero
intero (numero quantico principale n)
Le funzioni d’onda che per quei dati valori di energia sono soluzioni
dell’equazione (autofunzioni) sono funzioni matematiche alquanto
complesse che contengono tre numeri quantici e restano definite
dagli specifici valori di questi.
Ogni autofunzione associata ad una definita terna di numeri quantici
è chiamata ORBITALE.
Un orbitale non ha un significato fisico ma lo ha il suo quadrato, che
rappresenta la probabilità di trovare l’elettrone in una data regione
dello spazio.
Ψ può assumere valori positivi, negativi o nulli (nodi).
In questi ultimi la probabilità di trovare l’elettrone è 0
18
Ricapitolando
n1
numero quantico principale
0 l n-1
numero quantico secondario
-l ml l
numero quantico magnetico
19
20
La funzione d’onda si trova risolvendo l’equazione di
Schrödinger della particella con i vincoli imposti dalle condizioni
al contorno. Si trova che la particella è in grado di possedere
solo determinate energie!
21
Nell’atomo di idrogeno:
ε0= permettività nel vuoto
22
n
l
m
1
0
0
1,0,0
s
2
0
0
2,0,0
s
2
1
-1
2,1,-1
2
1
0
2,1,0
2
1
+1
2,1,-1
3
0
0
3,0,0
3
1
-1
3,1,-1
3
1
0
3,1,0
3
1
+1
3,1,-1
3
2
-2
3,2,-2
3
2
-1
3,2,-1
3
2
0
3,2,0
3
2
+1
3,2,1
3
2
+2
3,2,2
p
s
p
d
23
x = r sin cos
y = r sin sin
z = r cos
Alcuni autori trovarono più conveniente
esprimere la funzione d’onda in
funzione delle coordinate sferiche.
In questo modo la funzione d’onda può essere
considerata il prodotto di due componenti:
( r ) ( , )
24
25
Gli orbitali atomici.
n=1. Orbitale 1s
26
Gli orbitali atomici.
n=2. Orbitali 2s e 2p
27
Gli orbitali atomici.
n=3. Orbitali 3d
28
Bisogna quindi immaginare l’elettrone come diffuso nello spazio
attorno al nucleo in zone in cui è massima la probabilità di
trovarlo.
Queste zone sono delimitate da superfici limiti che racchiudono
il 90 % (non si può mai escludere che l’elettrone se ne trovi al di
fuori) della probabilità di trovare l’elettrone ed è proprio con
queste superfici che i chimici ricavano informazioni sugli atomi e
sulle molecole.
Gli orbitali s hanno sempre una simmetria sferica, cioè la
probabilità di trovare l’elettrone è sempre la stessa in tutte le
direzioni a partire dal nucleo.
Tutti gli altri orbitali hanno proprietà direzionali, cioè la
probabilità di trovare l’elettrone a partire dal nucleo ha direzioni
privilegiate.
Come vedremo questo è la causa della formazione delle
geometrie molecolari.
29
Ψ2(r,θ,ϕ)
30
31
32
33
34
Il numero quantico di spin
Facendo passare un fascio di atomi di idrogeno attraverso un forte campo
magnetico, il fascio si separa in due parti che seguono traiettorie diverse :
l’elettrone si comporta come una carica che “ruota” su se stessa producendo
un campo magnetico (STERN e GERLACH, Ag)
N
S
35
Stern and Gerlach
36
Il cloruro MeClx ha pesoformula =133,35 uma e l’ossido
Me2Oy ha pesoformula = 101,96 uma. Noto che il metallo
Me ha lo stesso numero di ossidazione nei due composti,
se ne calcoli il peso atomico (PA(Cl)=35,45 uma;
PA(O)=16,00 uma).
Da 2,000 g dell’ossido Me2O trattati con HCl acquoso in
eccesso, si ottengono g 3,771 di MeCl. Si calcoli il peso
atomico di Me (PA(Cl)=35,45 uma; PA(O)=16,00 uma).
37
E’ dato un campione impuro di arsenito di
potassio, KAsO2, del peso di 1,48 g. Si
determini la quantità di KAsO2 presente,
sapendo che, dopo trattamento del campione
con eccesso di Zn in ambiente acido,
l’arsina, AsH3, formata viene ossidata
completamente ad acido arsenico, H3AsO4,
da 6,82 g di I2. Lo iodio si riduce a I-.
PA(I) = 126,904 uma; PA(As) = 74,922 uma;
PA(O) = 15,999 uma; PA(K) =39,098 uma.
38











