Funzioni

Capitolo 4
Funzioni
4.1
Il concetto di funzione
Nella matematica, ed in molte delle sue applicazioni scientifiche e tecniche, si ha molto spesso
la necessità di considerare grandezze appartenenti ad un certo insieme B che dipendono
da grandezze appartenenti ad un altro insieme A, la dipendenza essendo espressa da una
relazione in base alla quale una volta fissato un elemento dell’insieme A resta ben determinato
il corrispondente elemento dell’insieme B.
La dipendenza tra le grandezze può essere di natura svariata. La forma della relazione
può essere tale da non consentire una scelta arbitraria dell’elemento di A, vale a dire che la
relazione risulta operante solo su un certo sottoinsieme E di A. Considereremo, da qui in
avanti, quelle relazioni che rispondono alla definizione di funzione formulata nel capitolo 1.
Ciò che caratterizza specificamente il concetto di funzione — nell’accezione in cui ora
ci interessa particolarmente — è la natura degli insiemi delle grandezze coinvolte. Questi
saranno sempre insiemi di punti di spazi euclidei (o, comunque, ad essi assimilabili). E si
tratterà, in generale, di spazi euclidei di dimensione da 1 a 3. Rimandando a più avanti
l’esame delle situazioni in cui uno od entrambi gli insiemi A e B appartengano a spazi a più
dimensioni, ci occuperemo qui del caso in cui entrambi appartengano allo spazio R (o R 1 ):
ciò definisce le funzioni (reali) di una variabile (reale).
4.2
Funzioni di una variabile
Tutte le volte che, dato un certo insieme E di punti dell’asse x, esiste una legge che consente
di associare ad ogni punto x ∈ E un determinato numero reale y, si dirà che y è una funzione
della variabile x (o del punto x), definita nell’insieme E. Per indicare questo concetto si
usa la rappresentazione y = f (x). Affinché la legge cosı̀ espressa risulti consistente con il
concetto di funzione deve verificarsi che ad ogni punto dell’insieme E, ove la funzione è
definita, corrisponda uno ed un solo valore y della funzione f .
Quando si afferma che la funzione f (x) è definita nell’insieme E si vuole intendere che il
numero y = f (x) risulta sicuramente determinato in corrispondenza ad ogni punto x ∈ E.
Per un punto x ∈
/ E non si può dire nulla circa il valore f (x) della funzione. In generale, ciò
dipenderà dal fatto che la legge che definisce tale valore perde significato quando x è fuori
di E, ma può anche esprimere che non siamo interessati a considerare tale legge per punti x
fuori di E. Se una funzione f (x) è definita nell’insieme E, essa risulta anche definita in ogni
insieme G ⊂ E; si dice, in questo caso, che si considera la restrizione di f all’insieme G.
23
Capitolo 4. Funzioni
Se f (x) è definita nell’insieme E, ad ogni punto x ∈ E corrisponde il valore y della
funzione e, al variare di x in E, tutti i valori x che si ottengono costituiscono un certo
insieme F di numeri reali che si chiama il coinsieme della f (x) in E. Si può dire che la
funzione f (x) trasforma l’insieme E nel coinsieme F , oppure che realizza un’applicazione di
E in F . Ciò viene anche indicato con la notazione
f : E → F.
(4.1)
Può accadere che il coinsieme F sia costituito da un solo punto: in tal caso la funzione si
dice costante nell’insieme E.
Generalmente per definire una funzione si utilizza una formula, come ad esempio
1
,
1−x
(4.2)
y = loga x.
(4.3)
y=
oppure
In tal caso si considera come insieme di definizione l’insieme E costituito dai numeri x
per i quali la formula abbia senso, cioè per i quali sia possibile eseguire le operazioni indicate
nella formula.
Ad esempio, la (4.2) non ha senso per x = 1, quindi E = (−∞, 1) ∪ (1, +∞). La (4.3) ha
senso solo se è x > 0, quindi E = (0, +∞).
4.3
Grafico di una funzione
Per le funzioni y = f (x) di una variabile si può dare la seguente rappresentazione geometrica.
Si segnano su un piano due assi cartesiani ortogonali x, y e sull’asse x si considera l’insieme
E dei punti in cui la funzione f (x) è definita; quindi, per ogni punto x ∈ E, si costruisce il
punto del piano che ha ascissa uguale a x e ordinata uguale al valore y = f (x) della funzione
f nel punto x. Si ottiene cosı̀ nel piano un insieme di punti Γ: la figura formata da tali punti
costituisce quello che si chiama il grafico della funzione. I punti di Γ costituiscono anche un
sottoinsieme del prodotto cartesiano E × F , definito da
Γ = {(x, y)| x ∈ E, y ∈ F, y = f (x)}.
Nei casi che più comunemente si presentano l’insieme E è costituito da un intervallo o
dall’unione di più intervalli dell’asse x. In tal caso il grafico della funzione è costituito da
uno o più rami di curva e, per questo motivo, il grafico della funzione y = f (x) viene anche
detto curva di equazione y = f (x).
Vedremo ora, a titolo di esempio, i grafici di alcune importanti funzioni, per delineare
i criteri che aiutano a determinarne l’andamento e cominciare a familiarizzare con le loro
proprietà.
24
4.3. Grafico di una funzione
Grafico della funzione y = ax + b.
L’insieme E di definizione della funzione è l’intervallo (−∞, +∞); il grafico (figura 4.1) è
una retta che incontra l’asse y nel punto di ordinata b ed ha il coefficiente angolare uguale
ad a (vale a dire forma con l’asse x un angolo α tale che tan α = a).
y
y =x+2
3
2
1
−6
−5
−4
−3
−2
1
−1
−1
2
3
4
5
x
Figura 4.1: Grafico della funzione y = x + 2.
Grafico della funzione y = ax 2 .
L’insieme E di definizione della funzione è l’intervallo (−∞, +∞); il grafico (figura 4.2) è
una parabola con il vertice nell’origine.
y
5
4
3
2
y=
1 2
x
2
1
−5
−4
−3
−2
1
−1
2
Figura 4.2: Grafico della funzione y =
25
3
1 2
x .
2
4
x
Capitolo 4. Funzioni
Grafico della funzione y =
a
.
x
L’insieme E di definizione della funzione è costituito dall’unione degli intervalli (−∞, 0) e
(0, +∞); il grafico (figura 4.3) è una curva composta di due rami che si chiama iperbole
equilatera.
y
4
3
2
3
x
y=
1
−5
−4
−3
−2
1
−1
−1
2
3
x
4
−2
−3
−4
−5
Figura 4.3: Grafico della funzione y =
3
.
x
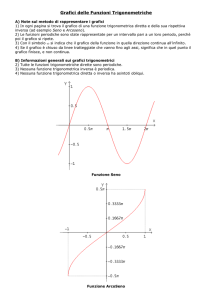
Grafici delle funzioni y = sin x e y = cos x.
Queste due funzioni sono definite nell’intervallo (−∞, +∞); i loro grafici (figura 4.4) hanno
lo stesso andamento e differiscono per uno spostamento dell’argomento pari a π/2.
y
y = cos x
−
3π
2
−π
−
1
π
2
y = sin x
π
2
π
3π
2
−1
Figura 4.4: Grafici delle funzioni y = sin x e y = cos x.
26
x
4.3. Grafico di una funzione
Grafici delle funzioni y = tan x e y = cot x.
La funzione
sin x
cos x
è definita per i punti x in cui cos x 6= 0 e quindi in tutto l’intervallo (−∞, +∞) esclusi i punti
y = tan x =
x = (2 k + 1)
π
2
con k intero relativo; analogamente, la
y = cot x =
cos x
sin x
è definita per i punti x in cui sin x 6= 0 e quindi in tutto l’intervallo (−∞, +∞) esclusi i punti
x = 2 k π.
I grafici sono mostrati nella figura 4.5.
y
2
y = tan x
1
−
3π
2
−π
−
π
2
π
2
π
3π
2
x
−1
−2
y
2
y = cot x
1
−π
−
π
2
π
2
π
3π
2
−1
−2
Figura 4.5: Grafici delle funzioni y = tan x e y = cot x.
27
x
Capitolo 4. Funzioni
Grafico della funzione y = loga x.
Si suppone naturalmente la base a positiva e diversa da 1; la funzione è definita nell’intervallo
aperto (0, +∞). Il grafico (curva logaritmica) si presenta in due modi diversi a seconda che
sia a > 1 oppure a < 1. I due grafici sono mostrati nella figura 4.6.
y
y = log2 x
3
2
1
1
2
3
4
5
6
7
x
8
−1
−2
y = log
−3
1/2
x
Figura 4.6: Grafici delle funzioni y = log2 x e y = log
1/2
x.
Grafico della funzione y = a x .
Si suppone a > 0 ed allora la funzione è definita nell’intervallo (−∞, +∞). Se a = 1 la
funzione è costante; se a 6= 1 Il grafico (curva esponenziale) si presenta in due modi diversi
a seconda che sia a > 1 oppure a < 1. I due grafici sono mostrati nella figura 4.7.
y
5
4
x
1
y=
2
y = 2x
3
2
1
−4
−3
−2
1
−1
2
3
4
Figura 4.7: Grafici delle funzioni y = 2 x e y = (1/2) x .
28
x
4.3. Grafico di una funzione
Grafici delle funzioni circolari inverse.
Dato un numero x ci proponiamo di trovare tutti i numeri y il cui seno è uguale a x. È
evidente che affinché il problema abbia soluzione occorre che sia −1 6 x 6 1; inoltre, è
chiaro che di tali numeri y ne esistono infiniti. Però fra questi infiniti valori di y ne esiste
uno solo che appartenga all’intervallo [−π/2, π/2]. Tale numero sarà chiamato l’arco il cui
seno è x e si scriverà y = arcsin x, che rappresenta una funzione definita nell’intervallo [−1, 1].
In modo del tutto analogo si definisce nell’intervallo [−1, 1] la funzione arco il cui coseno
è x, che si scrive y = arccos x, con l’intesa di prendere, per ogni x, il valore di y appartenente
all’intervallo [0, π]. I grafici delle funzioni y = arcsin x e y = arccos x sono mostrati nella
figura 4.8.
y
π
y = arccos x
π
2
−4
−3
−2
1
−1
y = arcsin x
−
2
3
4
x
π
2
Figura 4.8: Grafici delle funzioni y = arcsin x e y = arccos x.
Infine si definisce nell’intervallo (−∞, +∞) la funzione arco la cui tangente è x, che si
scrive y = arctan x ed il cui grafico è mostrato nella figura 4.9.
y
π
2
y = arctan x
−7
−6
−5
−4
−3
−2
1
−1
−
2
3
4
π
2
Figura 4.9: Grafico della funzione y = arctan x.
29
5
6
7 x
Capitolo 4. Funzioni
4.4
Alcune definizioni e proprietà relative alle funzioni
Una funzione f (x) definita in un insieme E si dice crescente [non decrescente] in tale insieme
quando, comunque si prendano in E due punti x0 , x00 con x0 < x00 , risulta f (x0 ) < f (x00 )
[f (x0 ) 6 f (x00 )]. Si dice decrescente [non crescente] se da x0 < x00 segue f (x0 ) > f (x00 )
[f (x0 ) > f (x00 )].
Le funzioni crescenti, non decrescenti, decrescenti, non crescenti in un dato insieme E si
designano complessivamente col nome di funzioni monotone in tale insieme. La monotonia
di una funzione ha un’immediata interpretazione nel suo grafico: per una funzione crescente
[decrescente] il grafico sale verso destra [verso sinistra] ed analogamente per una funzione
non decrescente [non crescente].
Se l’insieme E di punti dell’asse x in cui è definita la f (x) è un insieme simmetrico rispetto
all’origine, ad ogni punto x ∈ E si può associare il punto −x ∈ E e si possono considerare i
due valori f (x), f (−x) della funzione. Se risulta
f (−x) = f (x),
∀x ∈ E
(4.4)
si dice che y = f (x) è una funzione pari. Se risulta
f (−x) = −f (x),
∀x ∈ E
(4.5)
si dice che y = f (x) è una funzione dispari.
È chiaro che il grafico di una funzione pari risulta simmetrico rispetto all’asse delle
ordinate, mentre il grafico di una funzione dispari risulta simmetrico rispetto all’origine delle
coordinate.
È anche ovvio che in generale una funzione non risulta né pari né dispari; però, scrivendo
f (x) + f (−x) f (x) − f (−x)
+
,
(4.6)
2
2
si vede che ogni funzione può essere considerata come la somma di una funzione pari e di
una funzione dispari.
f (x) =
Vediamo ora alcune categorie notevoli di funzioni.
Una prima categoria è costituita dai polinomi in x, definiti in (−∞, +∞) da formule del
tipo
y = a0 x n + a1 x n−1 + . . . + an−1 x + an , (a0 6= 0),
ove n è il grado del polinimio e a0 , a1 , . . . , an sono delle costanti.
Una seconda categoria è data dalle funzioni razionali di x, che sono espresse dal rapporto di due polinomi in x. Sono funzioni definite nell’insieme che si ottiene dall’intervallo
(−∞, +∞) togliendo gli eventuali punti in cui si annulla il polinomio denominatore.
30
4.5. Funzioni composte
In queste due categorie di funzioni si opera sulla variabile x soltanto con le quattro operazioni elementari (addizione, sottrazione, moltiplicazione, divisione); se ad esse si aggiunge
l’operazione di estrazione di radice, si ottiene una vasta classe di funzioni alle quali si può
dare il nome di funzioni algebriche della variabile x.
Sempre rimanendo nell’ambito delle funzioni esprimibili per mezzo di formule, si può
pensare a funzioni definite da espressioni in cui si opera sulla variabile, oltre che con le
operazioni algebriche, anche con i simboli loga , sin, cos, tan, cot, arcsin, arccos, arctan, oppure
in cui le variabili compaiono ad esponente. Tali funzioni si dicono non algebriche oppure
trascendenti.
Data la f (x) definita in E, consideriamo un qualsiasi G ⊆ E. La f (x) si dirà limitata
inferiormente, limitata superiormente, limitata in G se, rispettivamente, risulta limitato
inferiormente, limitato superiormente, limitato il coinsieme della f (x) in G.
Chiameremo estremo inferiore o estremo superiore della f (x) in G rispettivamente l’estremo
inferiore o l’estremo superiore del coinsieme di f (x) in G; tali estremi possono essere finiti o
infiniti. Se l’estremo inferiore [superiore], supposto finito, appartiene al coinsieme di f (x) in
G, se cioè è un minimo [massimo] per tale coinsieme, diremo che la f (x) è dotata di minimo
[massimo] assoluto nell’insieme G. Dire, ad esempio, che f (x) è dotata di massimo assoluto
in G significa che, al variare di x in G, l’insieme dei valori assunti dalla f (x) ha un estremo
superiore finito Λ e che questo numero Λ è un valore effettivamente assunto dalla funzione,
vale a dire che esiste almeno un x0 ∈ G tale da aversi f (x0 ) = Λ.
Se l’estremo inferiore e l’estremo superiore sono entrambi finiti, la loro differenza è un
numero non negativo che si chiama l’oscillazione della f (x) in G. Se uno almeno dei predetti
estremi non è finito diremo che l’oscillazione della f (x) in G è infinita. Si può anche dire che
l’oscillazione di f (x) in G è uguale all’estremo superiore dell’insieme descritto dal numero
|f (x0 ) − f (x00 )| al variare dei punti x0 e x00 in G.
4.5
Funzioni composte
La funzione f (x) sia definita nell’insieme E (di punti dell’asse x) ed abbia per coinsieme
l’insieme F (di punti dell’asse y). Supponiamo che F sia contenuto in un certo insieme H
(di punti dell’asse y) nel quale sia definita una funzione u = ϕ(y) della variabile y.
In tali condizioni possiamo dire che per ogni punto x ∈ E resta determinato, mediante
la y = f (x), un punto y ∈ H e quindi anche individuato il valore u = ϕ(y) della funzione ϕ.
Ne deriva che u può pensarsi, oltre che funzione della variabile y, anche funzione della x, la
dipendenza di u da x avvenendo per il tramite della y. In sostanza, per calcolare la u come
funzione di x, occorre prima calcolare la y = f (x) e poi sostituire il valore trovato nella ϕ,
per cui si può scrivere
u = ϕ[f (x)].
31
Capitolo 4. Funzioni
Questa nuova funzione u della variabile x, definita in E, si chiama funzione composta
mediante la funzione ϕ (della variabile y, definita in H) e la funzione f (della variabile x,
definita in E).
L’operazione di composizione delle funzioni può essere ripetuta più volte e si possono cosı̀
generare, a partire dalle funzioni più comuni, delle altre funzioni via via più complicate.
32