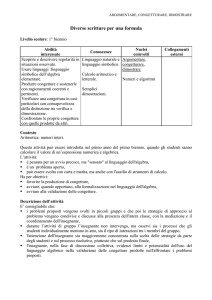
Costruzione di espressioni rappresentanti particolari
proprietà dei numeri Naturali
Nell’approccio all’algebra risultano molto importanti lo sviluppo della capacità di assegnare “nomi
appropriati” a entità coinvolte nella soluzione di problemi e di costruire espressioni per interpretare
situazioni problematiche o descrivere fenomeni. Per sviluppare queste capacità può essere molto
utile svolgere attività centrate sulla costruzione e dimostrazione di congetture relative a proprietà
dei numeri. AlNuSet può svolgere un ruolo molto importante nello sviluppo delle capacità indicate.
Consideriamo il seguente compito. Vogliamo esplorare cosa succede se si sommano due numeri
dispari consecutivi.
Un esempio di testo per gli studenti può essere il seguente:
“Nell’ambiente di AlNuSet seleziona il dominio dei numeri naturali, usa appropriati nomi per
indicare in modo generale due numeri dispari consecutivi, rappresenta tali nomi sulla Retta
Algebrica e verifica che superino il test del trascinamento (si veda successivamente). Usa tali nomi
per scrivere l’espressione che rappresenta la somma di due numeri dispari consecutivi e usa la
Retta Algebrica per esplorare la proprietà che caratterizza i numeri da essa indicati. Esprimi
questa proprietà con un enunciato. Esprimi l’espressione in un’altra forma che consenta di
evidenziare più esplicitamente la proprietà individuata. Usa il test del trascinamento per verificare
che le espressioni sono tra loro equivalenti.”
Il test di trascinamento citato nel del testo consiste nella verifica che i nomi rappresentati sulla retta
indicano una coppia di numeri dispari consecutivi durante il trascinamento dei punti mobili. Se uno
studente usa come nomi, per esempio, x e y, oppure d e d 2 (evento piuttosto frequente), il test di
trascinamento consente immediatamente di evidenziare che essi non sono appropriati per indicare
una qualsiasi coppia di numeri dispari e consecutivi. Lo sfruttamento sul piano didattico di questa
funzione di validazione permette di attuare un insegnamento specifico sulla nominalizzazione, di
difficile realizzazione senza l’uso della Retta Algebrica. Inoltre, nella soluzione di questo compito,
il trascinamento del punto mobile svolge anche una funzione didattica di mediazione nella
costruzione e nella verifica di congetture. Infatti, rappresentata sulla retta l’espressione relativa alla
somma di due numeri dispari consecutivi ( 2 x 1 2 x 3 ), il trascinamento del punto x può essere
usato per esplorare e cogliere regolarità numeriche in ciò che questa espressione indica. Il
trascinamento può, infine, essere usato per verificare che esistono forme equivalenti
dell’espressione ( 4 x 4 , 4 x 1 ) in grado di evidenziare con più efficacia la proprietà
individuata. Il test di trascinamento consente di validarne l’equivalenza.