The Feyman Lectures on Physics: SCHEDULES
La fisica di Feynmann
Tabelle
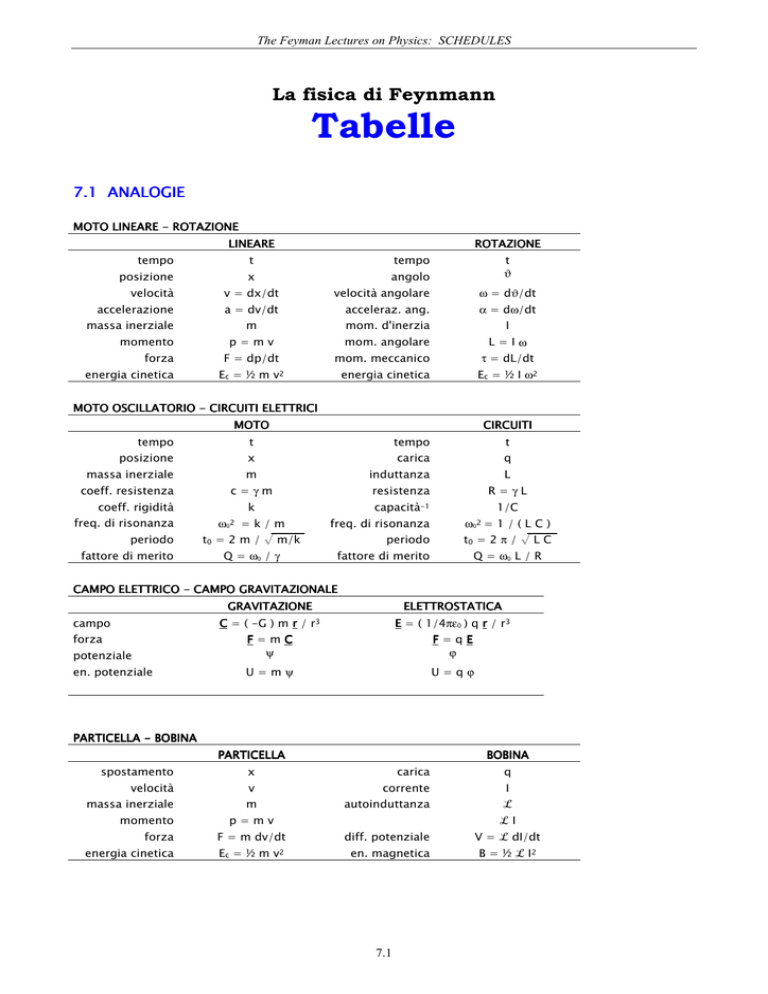
7.1 ANALOGIE
MOTO LINEARE - ROTAZIONE
LINEARE
ROTAZIONE
tempo
t
tempo
posizione
x
angolo
velocità
accelerazione
massa inerziale
momento
forza
energia cinetica
v = dx/dt
a = dv/dt
velocità angolare
p=mv
Ec = ½ m v2
ω = dϑ/dt
acceleraz. ang.
m
F = dp/dt
t
ϑ
α = dω/dt
mom. d'inerzia
I
mom. angolare
L=Iω
mom. meccanico
τ = dL/dt
energia cinetica
Ec = ½ I ω2
MOTO OSCILLATORIO - CIRCUITI ELETTRICI
MOTO
tempo
posizione
massa inerziale
coeff. resistenza
coeff. rigidità
freq. di risonanza
periodo
fattore di merito
CIRCUITI
t
tempo
m
induttanza
k
capacità-1
x
c=γm
q
L
resistenza
ω02 = k / m
freq. di risonanza
Q = ω0 / γ
fattore di merito
t0 = 2 m / √ m/k
t
carica
periodo
R=γL
1/C
ω02 = 1 / ( L C )
t0 = 2 π / √ L C
Q = ω0 L / R
CAMPO ELETTRICO - CAMPO GRAVITAZIONALE
GRAVITAZIONE
ELETTROSTATICA
C = ( -G ) m r / r3
potenziale
F=mC
ψ
E = ( 1/4πε0 ) q r / r3
en. potenziale
U=mψ
U=qϕ
campo
forza
F=qE
ϕ
PARTICELLA - BOBINA
PARTICELLA
BOBINA
spostamento
x
carica
q
velocità
v
corrente
I
massa inerziale
momento
forza
energia cinetica
m
autoinduttanza
F = m dv/dt
diff. potenziale
p=mv
Ec = ½ m v2
en. magnetica
7.1
ℒ
ℒI
V = ℒ dI/dt
B = ½ ℒ I2
The Feyman Lectures on Physics: SCHEDULES
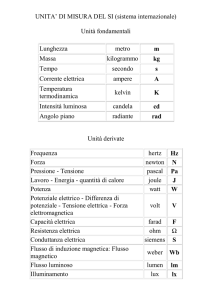
7.2 GRANDEZZE E COSTANTI
Grandezze fondamentali
Unita S.I.
Lunghezza (s,x,y,z,r)
m (metro)
s (secondo)
t
Massa (m)
kg (kilogrammo)
m
Corrente elettrica (I)
A (ampere)
I
Tempo (t)
Temperatura (T)
Angolo piano
r
K (kelvin)
rad (radiante)
T
Grandezze derivate
Lunghezza e massa
Momento d'inerzia (I)
Superficie (A)
m2
Volume (V)
m3
Densità (ρ)
CINEMATICA (lunghezza e tempo)
I = ∑ mi ri2
ρ=
Accelerazione (a)
m s-2
Accelerazione angolare (α)
rad s-2
Frequenza (ν)
Lunghezza d'onda (λ)
a = dv
v/dt
α = dω
ω/dt
Hz (hertz)
m
ν=
λ=
m-1
Numero d'onda (k)
rad
Oscillazione o freq. angolare (ω)
rad s-1
ω=
m s-1
v = drr/dt
Periodo (t0)
s
Velocità angolare (ω)
rad s-1
Velocità (v)
k=
t0 =
[v=ω∧r]
DINAMICA (lunghezza, tempo e massa)
Forza (F)
N (newton)
F = dp
p/dt
Energia cinetica (EC)
J (joule)
Ec = ½ m ( v ⋅ v )
Energia (E)
Energia potenziale (U)
Lavoro (W)
Momento angolare (L)
Momento meccanico (τ)
Potenza (P)
J (joule)
J (joule)
s₂
J (joule)
W = ∫ F ds
s
s₁
L=r∧p
τ=r∧F
W (watt)
P=F⋅v
Quantità di moto (p)
TERMODINAMICA (lunghezza, massa, tempo e temperatura)
Entalpia (H)
Entropia (S)
Flusso termico
J (joule)
J grado-1
Intensità di campo gravitazionale (C)
C = - G m r / r3
Potenziale gravitazionale (ψ)
Carica elettrica (q)
Densità di carica elettrica (ρ)
ψ = -∫ C ds
s
C (coulomb)
[ I = dq/dt ]
ρ=
Densità di corrente elettrica (j)
Forza elettrica (F)
H = U + PV
S = Q/T
GRAVITAZIONE (lunghezza, massa e tempo)
ELETTROMAGNETISMO
p=mv
j=
F=q(E+v∧B)
Capacità elettrica (C)
F (farad)
C=q/V
Induttanza elettrica (L)
H (henry)
[ V = L (dI/dt) ]
Differenza di potenziale (V)
V (volt)
7.2
The Feyman Lectures on Physics: SCHEDULES
Intensità di campo elettrico (E)
E = q r / ( 4πε0 r3 )
Potenziale elettrico (φ)
Resistenza elettrica (R)
MAGNETISMO
Induzione magnetica (B)
Intensità di campo magnetico (B)
φ = -∫ E ds
s
Ω (ohm)
R=V/I
T (tesla)
weber m-1
Costanti
Meccanica
Costante G
G = 6.670 ⋅ 10-11 [ N m2 / kg2 ]
Numero di Avogadro
N0 = 6.02 ⋅ 1023
Termodinamica
Costante di Boltzmann
R
Elettromagnetismo
k = 1.38 ⋅ 10-23 [ J / K ]
R = N0 k = 8.317 [ J / mol K ]
Velocità della luce
c ≅ 3 ⋅ 108 [ m / s ]
1 / ( 4π ε0 )
1 / ( 4π ε0 ) ≅ 9.0 ⋅ 109 [ N m2 / C2 ]
Permettività del vuoto
ε0 = 8.854 ⋅ 10-12 [ C2 / N m2 ]
Impedenza del vuoto
1/ ( ε0 c ) = 377 [ Ω ]
Carica di un elettrone
qe = 1.602 ⋅ 10-19 [ C ]
Raggio classico dell'elettrone
r0 = e2 / me c2
e2
Meccanica quantistica
e2 = qe2 / ( 4π ε0 ) = 2.3068 ⋅ 10-28 [ N m2 ] ; e = 1.5188 ⋅ 10-14
Costante di Planck
h = 6.626 ⋅ 10-34 [ J s ]
Raggio di Bohr
a0 = 0.528 [ Å ]
ћ=
Energia di ionizzazione dell'idrogeno E0 = -13.6 [ eV ]
Costante del corpo nero
s = K4 π2 / 60 ћ3 c2 = 5.67 ⋅ 10-8 [ W / m2 grado4 ]
7.3