Esercizio #1
Un importante annuncio è trasmesso, per mezzo di onde radio, a persone sedute vicino alle proprie
radio ad una distanza di 100 Km dall'emittente e, per mezzo di onde sonore, alle persone sedute
nella sala stampa a 3 m dallo speaker. Considerando che la velocità del suono nell'aria è uguale a
343 m/s, chi riceve per primo la notizia? Spiegare il perché.
Le persone alla radio, perché te.m. = 0. 333 ms, ts = 8.746 ms
Esercizio #2
Una lampadina da 100 W emette onde elettromagnetiche sferiche uniformemente in tutte le
direzioni. Trovare (a) la potenza media per unità di superficie, (b) l’intensità del campo magnetico
B e (c) del campo elettrico E alla distanza d = 3 m dalla lampadina, supponendo che solo metà della
potenza si converta in radiazione elettromagnetica. (d) Indicare direzione e verso del vettore di
Poynting nel punto a distanza d dalla lampadina?
P = 100 W
d=3m
(a) I = 0.884 W/m2 (b) E = 25.2 V/m (c) B = 8.40 10-8 T
Soluzione
(a) La lampadina emette come una sorgente puntiforme, ovvero emette la stessa quantità di
radiazione in tutte le direzioni. Quindi la potenza che irraggia ad una distanza d è distribuita su una
sfera centrata nella lampada stessa e con raggio pari a d = 3m. Quindi, data la potenza media
emessa dalla lampada P = 100 W, dividiamo per la superficie della sfera e otteniamo la potenza per
unità di superficie, ovvero l'intensità I della lampada:
I=
P
100 W
=
= 0.884 W/m 2
2
2
2
4π d
4π 3 m
(b, c) Dato che la potenza media per unità di superficie può essere espressa in funzione del campo
elettrico Emax e campo magnetico Bmax dalla relazione:
I=
2
Emax Bmax
E2
c Bmax
= max =
2 µ0
2 µ0 c
2 µ0
è possibile ricavare il valore di Emax e Bmax:
Emax = 2 I µ 0 c = 2 * 0.844
Bmax
2 I µ0
=
=
c
W
Tm
m
V
* 4π 10 −7
* 3 108 = 25.2
2
m
A
s
m
2 * 0.844
W
Tm
* 4π 10 −7
2
m
A = 8.40 10 −8 T
m
3 10 8
s
(d) Il vettore di Poynting sarà diretto verticalmente nella direzione di propagazione dell'onda
elettromagnetica emessa dalla lampadina, quindi verso il basso.
Esercizio #3
Una comunità progetta di costruire un impianto per convertire la radiazione solare in energia
elettrica. La comunità richiede 1 MW di potenza e il sistema da installare ha un rendimento del 12%
(cioè 12% dell’energia solare incidente sulla superficie viene convertita in energia utile).
Assumendo che la luce solare abbia un’intensità costante di 1000 W/m2, quale deve essere l'area
effettiva dei pannelli fotovoltaici perfettamente assorbenti utilizzati in un tale impianto?
A = 3.33 103 m2
Esercizio #4
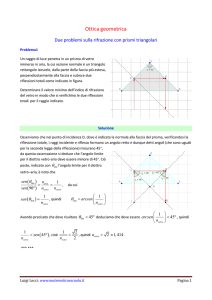
Inclinando opportunamente uno specchio piano si vuole illuminare il fondo di un pozzo sfruttando
la luce solare mentre il Sole forma un angolo α = 36° sopra l'orizzonte. Determinare l'angolo β
formato tra lo specchio e il terreno.
β = 63°
Soluzione
Per poter illuminare il fondo del pozzo, lo specchio deve essere posizionato in modo tale che il
raggio di sole sia riflesso verticalmente e l'angolo formato dal raggio incidente e da quello riflesso
sarà dato dalla somma di α e 90° (vedi figura).
Ricordando che, in base alla legge della riflessione, l'angolo ϑi (formato dal raggio incidente sullo
specchio e la normale n allo specchio nel punto di incidenza) è uguale all'angolo ϑr (formato dal
raggio riflesso e la normale allo specchio), possiamo ricavare il valore di ϑi e ϑr:
ϑi + ϑr = α + 90°
α + 90° 36° + 90°
⇒ 2ϑi = α + 90° ⇒ ϑi =
=
= 63°
2
2
ϑi = ϑr
Quindi, facendo riferimento alla figura seguente, se consideriamo l'angolo di 90° formato dallo
specchio e dalla normale n, nella regione in cui giace il raggio incidente, possiamo ricavare
l'inclinazione dello specchio rispetto al terreno, ovvero l'angolo β richiesto:
β = (90° - ϑi) + α = (90° - 63°) + 36° = 63°
β
ϑr
α
ϑi
n
Esercizio #5
Un gatto (che non ha ripassato bene l'ottica geometrica) vede un pesce rosso appoggiato alla parete
di un acquario cilindrico di raggio R = 20 cm, a x = 10 cm dalla superficie dell'acqua. Felice del suo
imminente bocconcino, prende la mira... ma sbaglia clamorosamente bersaglio! A che quota si trova
realmente il pesce dalla superficie dell'acqua? L'indice di rifrazione dell'acqua è nH2O = 1.33.
R
x
h = 18.2 cm dalla superficie
Soluzione
ϑi
α
R
x
α
ϑr
h
L'angolo formato dalla superficie dell'acqua e dal prolungamento senza diffrazione del raggio
incidente (tratteggiato in rosso nella figura) è opposto al vertice all'angolo α, quindi vale anch'esso
α. Pertanto, considerando il triangolo rettangolo di cateti x e R, abbiamo che vale:
tg α = x/R = 10 cm / 20 cm = 0.5
quindi:
α = arctg (0.5) = 26.56°
Quindi l'angolo di incidenza dal raggio sull'acqua è dato da:
ϑi = (90° - α) = (90° - 26.56°) = 63.43°
Dalla legge di Snell della rifrazione, sappiamo che:
n1 sen(ϑi) = n2 sen(ϑr)
con indice di rifrazione dell'aria n1 = 1.0003 ≈ 1 e n2 = nH2O = 1.33. Quindi:
sen(ϑr) = sen(ϑi) / n2 = sen(ϑi) / 1.33
ϑr = arcsen( sen(ϑi) / 1.33 ) = arcsen( sen(63.43°) / 1.33 ) = arcsen( 0.894 / 1.33 ) = 47.69°
Quindi per calcolare la vera quota a cui si trova il pesce, consideriamo il triangolo rettangolo
formato dai cateti h ed R e l'angolo adiacente alla superficie dell'acqua dato da:
(90° - ϑr) = (90° - 47.69°) = 42.3°
Dalla relazione tg(42.3°) = h / R, ricaviamo il valore di h:
h = R * tg(42.3°) = 20 cm * 0.91 = 18.2 cm
quindi il gatto ha sbagliato la mira di 18.2 - 10 = 8.2 cm!
Esercizio #6
Su una lastra di materiale trasparente e di forma rettangolare incide della radiazione luminosa. Si
considerino i raggi che dopo aver inciso sulla faccia orizzontale ed essere stati rifratti incidono su
quella verticale. Quale deve essere l’indice di rifrazione n della lastra affinché tale raggio incidente
sulla parete verticale subisca riflessione totale, se α = 30°?
n = 1.11
Esercizio #7
Un raggio di luce monocromatica incide con un angolo di 54° su una lastra di vetro a facce piane
parallele, avente indice di rifrazione n = 1.62. Se lo spostamento d subito dal raggio luminoso è pari
a 0.8 cm, qual’é lo spessore della lastra?
h = 1.7 cm