Induzione elettromagnetica 1

[Adattato da AIF, Esempio di proposta di II prova scritta, 2014]
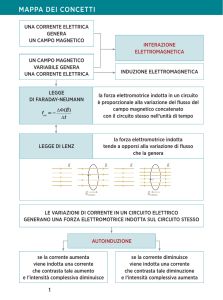
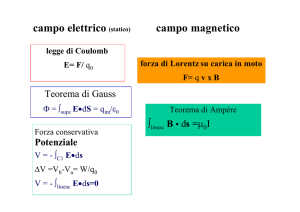
INDUZIONE ELETTROMAGNETICA
Si consideri un circuito rettangolare come quello mostrato in figura formato da un telaio fisso e
una sbarra conduttrice come quarto lato lunga 3 cm. Tale circuito è dotato di una resistenza del
valore noto R. Il circuito è immerso in un campo magnetico uniforme ortogonale al piano del
circuito d’intensità pari a 400 G (1 G = 10-4 T).
Il candidato:
a) Descriva sotto quali ipotesi si genera una f.e.m. indotta nel circuito e commenti le principali
leggi fisiche che descrivono il fenomeno.
[il telaio deve essere formato da materiale conduttore, la sbarretta deve essere in movimento
in modo che possa variare il flusso del campo magnetico, …; legge di Faraday-Neumann-Lenz,
eventualmente Leggi di Ohm.]
b) Dimostri che la Legge di Faraday-Neumann-Lenz può essere dedotta dall’azione della forza di
Lorentz che agisce sugli elettroni liberi del conduttore.
[La f.e.m. agli estremi della sbarra è pari a 𝐵𝑙𝑣 in quanto sugli elettroni liberi di tale sbarra si
esercita la forza di Lorenz con modulo pari a 𝐹 = 𝑞𝑣𝐵. A questa forza corrisponde un campo
elettrico costante del valore pari a 𝐸 = 𝐹/𝑞 = 𝑞𝑣𝐵/𝑞 = 𝑣𝐵 e quindi f.e.m.= 𝑣𝐵 ⋅ 𝑙.
c) Calcoli il valore della f.e.m. indotta se la barretta si muove con velocità costante pari a 2 cm/s
verso destra
𝑓. 𝑒. 𝑚. = 𝐵𝑙𝑣 = 400 ⋅ 10−4 ⋅ 3 ⋅ 10−2 ⋅ 2 ⋅ 10−2 = 24 𝜇𝑉
Si consideri ora un magnete tra le cui espansioni si produce un campo magnetico variabile nel
tempo la cui intensità (espressa in tesla) segue la legge 𝐵(𝑡) = 3 ⋅ 𝑒 −𝑡 . Una spira circolare di raggio
2 cm è immersa in questo campo e viene tenuta ferma.
Il candidato:
d) Rappresenti graficamente nel piano cartesiano la funzione B(t) in funzione del tempo.
e) Scriva l’espressione analitica che permette di calcolare la f.e.m. indotta nel circuito in funzione
di t e calcoli il valore della f.e.m. indotta nell’istante t=2 s.
𝑓. 𝑒. 𝑚. (𝑡) = −
𝑑Φ(𝐵)
𝑑B(t)
= −𝑆 ⋅
= −𝜋(2 ⋅ 10−2 )2 ⋅ 3 ⋅ 𝑒 −𝑡 ⋅ (−1) = 0,015 ⋅ 𝑒 −𝑡
𝑑𝑡
𝑑𝑡
𝑓. 𝑒. 𝑚. (𝑡 = 2) = 0,015 ⋅ 𝑒 −2 ≅ 2 𝑚𝑉
f) A quale velocità dovrebbe muoversi la barretta rappresentata in figura per ottenere lo stesso
valore della f.e.m. indotta nell’istante t=2 s precedentemente calcolata?
2 ⋅ 10−3 = 𝐵𝑙𝑣 → 2 ⋅ 10−3 = 400 ⋅ 10−4 ⋅ 3 ⋅ 10−2 ⋅ 𝑣 → 𝑣 =
≅ 1,7 𝑚/𝑠
2 ⋅ 10−3
400 ⋅ 10−4 ⋅ 3 ⋅ 10−2
g) Fornisca una giustificazione geometrica nel piano cartesiano del legame tra la f.e.m. indotta e il
flusso del campo magnetico.
[il valore istantaneo della f.e.m. indotta è la pendenza della retta tangente al grafico del flusso
del campo magnetico, cambiata di segno]