PRIMO PRINCIPIO DELLA TERMODINAMICA
1. Si calcoli il calore molare di un gas perfetto in una trasformazione reversibile
descritta dall’equazione VT k = cost , dove V e T sono il volume e la temperatura
assoluta del gas mentre k è una costante.
[c = cV − kR ]
2. n = 10 moli di gas perfetto vengono compresse isotermicamente ed in modo
reversibile passando da un volume Vi = 1 m3 ad un volume finale V f . Il gas è
contenuto in un recipiente adiabatico a contatto termico con un serbatoio di calore
costituito da una massa m = 0.1 kg di ghiaccio fondente alla temperatura di
t = 0 °C .
Sapendo
che
il
calore
latente
di
fusione
del
ghiaccio
è
λgh = 79.7 kcal kg , si determini il valore del volume finale V f per il quale si ha
completa fusione del ghiaccio.
m2λgh
3
V f = Vi exp −
= 0.23 m
nRT
3. n = 2 moli moli di gas perfetto monoatomico sono contenute in un recipiente a
pareti adiabatiche, chiuso da un pistone anch’esso adiabatico, di massa
trascurabile e sezione S = 10 cm 2 . Sul pistone è appoggiato un blocco di massa
m = 20 kg ed il pistone è in equilibrio alla temperatura T1 = 100 K . Si determini il
volume occupato dal gas sapendo che la pressione atmosferica esterna è
patm = 105 Pa . Successivamente il blocco viene rimosso ed il gas si espande fina a
raggiungere l’equilibrio alla pressione atmosferica esterna. Si calcoli la
temperatura finale di equilibrio T f .
peV1 + ncV T1
= 73.5 K
T2 =
nc p
4. Un recipiente a pareti rigide ed adiabatiche è costituito da due ampolle collegate
da un tubicino munito di valvola. Inizialmente la valvola è chiusa e nell’ampolla
di sinistra sono contenute n1 = 3 moli di He alla temperatura T1 = 300 K mentre
nell’ampolla di destra ci sono n2 = 2 moli di N 2 a temperatura T2 = 270 K . La
valvola viene aperta ed i gas si miscelano fino a raggiungere una condizione di
equilibrio. Calcolare la temperatura finale di equilibrio dei due gas, supponendo
che questi si comportino come gas perfetti.
3n1T1 + 5n2T2
≈ 284.2 K
T =
3n1 + 5n2
5. In un recipiente rigido adiabatico contenente n2 = 2 moli di un gas ideale
monoatomico a pressione p0 = 2 × 105 Pa e temperatura T0 = 300 K , viene
introdotto un solido di capacità termica C = 30 J K , alla temperatura T = 800 K .
Si determini la pressione finale del gas. Si trascurino la capacità termica del
recipiente ed il volume del solido.
3nRT0 + 2CT p0
5
p
=
=
×
3.82
10
Pa
f
3nR + 2C T0
6. Un gas ideale monoatomico è contenuto in un recipiente adiabatico alla pressione
p0 = 2 atm , collegato mediante una valvola ad un cilindro munito di pistone
soggetto ad una pressione esterna di pe = 1 atm . Inizialmente la valvola è chiusa
ed il gas si trova in equilibrio alla temperatura T1 = 300 K .La valvola viene aperta
lentamente ed il gas fluisce nel cilindro, fino a che si raggiunge una condizione di
equilibrio. Si determini la temperatura finale del gas.
4
T
=
f 5 Ti = 240 K
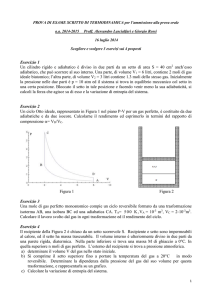
7. Un cilindro a pareti adiabatiche (a parte la parete di sinistra) è diviso in due parti
A e B da un setto adiabatico mobile e senza attrito; sia in A che in B ci sono
n = 1.2 moli di gas ideale biatomico alla pressione p0 = 1 bar ed alla temperatura
T0 = 300 K , eguale alla temperatura della sorgente di calore a contatto termico con
il gas in A . Si scalda molto lentamente il gas fornendogli il calore QB tramite una
resistenza elettrica e si attende che il sistema raggiunga uno stato di equilibrio in
cui la pressione vale pB = 1.3 bar . Determinare la temperatura finale del gas in B ,
il valore di QB e del calore QA scambiato dal gas in A con la sorgente.
p0
QA = LA = nRT0 ln = −745 J; TB = 469 K; QB = 4960 J
pB