Consideriamo lo sviluppo binomiale di

La precisione in matematica
Di Cristiano Armellini, [email protected]
Consideriamo il tema del calcolo dei decimali di un qualunque numero reale con una precisione infinita.
Consideriamo lo sviluppo binomiale di
(1 + 𝑥)𝑎 = 1 + 𝑎𝑥 + 𝐶2𝑎 𝑥 + 𝐶3𝑎 𝑥 + ⋯
Ove i termini dello sviluppo sono i coefficienti binomiali C.
Consideriamo quindi a = ½, a = 1/3 ecc.
Nel caso a = ½, per -1 < x <= 1 ho la seguente formula
1
1 2
1∗3 3 1∗3∗5 4
𝑥 +
𝑥 − 4
𝑥 +⋯
√1 + 𝑥 = 1 + 𝑥 −
2
2∗4
2∗4∗6
2 ∗ 4!
Per x = 1 ho immediatamente la √2
1
√3
Se x =1/2 ho posso calcolare √1 + 𝑥 = √1 + 2 = 2 ma sconoscendo già il valore esatto del denominatore
√
mi ricavo facilmente il valore del numeratore.
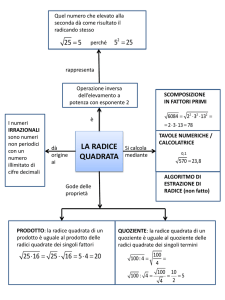
Continuando così per x = 1/3 mi calcolo la radice quadrata di 4 (che già so essere un quadrato perfetto),
quindi per x = ¼ mi calcolo la radice quadrata di 5, conoscendo la radice di 4, e per x = 1/5 la radice di 6
conoscendo già al passo precedente la radice quadrata di 5, ecc.
Il metodo iterattivo è immediato quando √1 + 1/𝑛 = √(𝑛 + 1)/𝑛 e n o n+1 sono quadrati perfetti perché
in questo caso applicando la formulo dello sviluppo binomiale e conoscendo il valore del quadrato perfetto,
il calcolo dell’altra radice quadrata risulta immediato.
Stesso ragionamento per le radici cubiche ricordando che per a = 1/3 (per -1 < x <= 1)
1
2 2
2∗5 3
𝑥 +
𝑥 +⋯
√1 + 𝑥 = 1 + 𝑥 −
3
3∗6
3∗6∗9
3
Il sistema descritto consente di ottenere valori con una precisione arbitraria ma a volte risulta poco pratico.
Consideriamo allora un’altra semplice tecnica. Partiamo dall’equazione 𝑥 2 + 𝑥 + 𝑐 = 0 che ha come
soluzioni 𝑥1,2 =
−1±√1−4𝑐
2
. Allora se il mio obiettivo è calcolare (ad esempio) la radice quadrata di 5 basterà
porre 1-4c=5, quindi c = -1, quindi 𝑥 2 + 𝑥 − 1 = 0, 𝑥 =
−1±√5
.
2
Per ottenere la soluzione in modo preciso
possiamo risolvere l’equazione usando i metodi del calcolo numerico (tangenti, Newton, punto unito,
bisezione) . Una volta trovato x basterà calcolare 2x+/-1 per ottenere il risultato finale.
E se devo calcolare la radice ennesima di x ? n > 2 . Si possono studiare regole ad hoc come abbiamo fatto
sopra per ogni n > 2 ma in generale si considera l’equazione 𝑥 𝑛 − 𝑎 = 0 che risolta con le tecniche di analisi
numerica dà la radice ennesima di a.
Un altro possibile approccio (sempre grazie a Taylor-Mc-Laurin) consiste nel considerare lo sviluppo di
𝑎 𝑥 = 𝑒 𝑥𝑙𝑛(𝑎) = 1 + 𝑥𝑙𝑛(𝑎) +
(𝑥𝑙𝑛(𝑎))2 (𝑥𝑙𝑛(𝑎))3
+
+⋯
2!
3!
Che vale per ogni x ma nella quale compare ln(a) ovvero il logaritmo naturale di a che però possiamo
calcolare con una precisione infinita usando una delle formule riportate qui sotto.
Usando lo sviluppo in serie di Taylor già sappiamo che possiamo calcolare con estrema accuratezza i valori
di sen(x), cos(x), tan(x), ln(x), alla base di molti calcoli e applicazioni matematiche (per l’accuratezza basterà
considerare molti termini della serie)
Ad esempio
𝑥3 𝑥5 𝑥7
+ − +. .
3! 5! 7!
𝑥2 𝑥4 𝑥6
cos(𝑥) = 1 − + − +. .
2! 4! 6!
2
𝑥
𝑥3
𝑒 𝑥 = 1 + 𝑥 + + +. .
2! 3!
𝑥−1
1 𝑥−1 3 1 𝑥−1 5
ln(𝑥) = 2 {(
)+ (
) + (
) +⋯},𝑥 > 0
𝑥+1
2 𝑥+1
5 𝑥+1
𝑠𝑒𝑛(𝑥) = 𝑥 −
𝑥−1
1 𝑥−1 2 1 𝑥−1 3
ln(𝑥) = {(
)+ (
) + (
) + ⋯ } , 𝑥 > 1/2
𝑥
2
𝑥
3
𝑥
Di queste espressioni sappiamo anche stimare l’errore che si commette considerando i primi k termini della
serie
La precisione è molto importante anche per il calcolo dei numeri trascendenti, il più famoso dei quali è
certamente il PI greco. Usando la formula di Wallis ho
𝜋
24𝑛 (4𝑛!)4
= lim
2 𝑛→+∞ [(2𝑛)!]2 (2𝑛 + 1)
Con questa formula molto compatta proviamo a scrivere una applicativo in Python per calcolare le cifre
decimali di pigreco con una precisione praticamente infinita
import math;
def wallis(n):
m = 10**n;
pi = ((2**(4*m))*(math.factorial(m))**4)/((2*m+1)*(math.factorial(2*m)**2));
k = 2*pi;
return k*10^n;
Ma in questo caso per ottenere una estrema precisione occorre disporre di un calcolatore particolarmente
potente