Scheda N° 2
NOTAZIONE SCIENTIFICA E ORDINE DI GRANDEZZA DI UN NUMERO
L’uso della notazione scientifica consente di valutare l’ordine di grandezza di un numero, molto utile per il
confronto fra misure omogenee.
La notazione scientifica è utile per svolgere dei calcoli e per esprimere correttamente il risultato di misure.
Nelle materie scientifiche si fa un grande uso delle potenze di 10, con esponenti sia positivi che negativi, per
rappresentare numeri molto grandi o molto piccoli.
I numeri molto grandi vengono scritti come prodotto di un coefficiente per l’opportuna potenza di 10 ad
esponente positivo.
I numeri molto piccoli vengono scritti come prodotto di un coefficiente per l’opportuna potenza di 10 a
esponente negativo.
Notazione scientifica
La regola per scrivere correttamente il numero in notazione scientifica è seguente: il numero deve essere
scritto come prodotto tra un coefficiente compreso tra 1 e 10:
1 ≤ c < 10
e opportuna potenza di 10.
(Nota: la virgola deve essere posta dopo la prima cifra diversa da zero.)
Esempio:
7
24 000 000 = 2,4 · 10
-6
0,00000321 = 3,21 · 10
L’ordine di grandezza
di un numero è la potenza di 10 più vicina al numero stesso. Serve per confrontare numeri che esprimono risultati di
misure. Per stabilire qual è l’ordine di grandezza conviene scrivere il numero in notazione scientifica e arrotondare il suo
coefficiente alla potenza di 10 più vicina, eseguendo le regole per approssimare i numeri riportate in tabella:
Se la cifra da approssimare
è seguita da:
una cifra < 5
5 seguita da 0 o da niente
5 seguito da un numero ≠ 0
una cifra > 5
si approssima per:
difetto
difetto
eccesso
eccesso
Prefissi delle unità di misura del Sistema Internazionale.
Nome
Simbolo
tera-
T
Fattore
10
giga-
G
10
mega-
M
10
kilo-
k
10
etto-
h
10
deca-
da
10
deci-
d
10
centi-
c
10
milli-
m
10
micro-
µ
10
nano-
n
10
pico-
p
10
12
9
6
3
2
1
-1
-2
-3
-6
-9
-12
Consigli:
1.
Per scrivere dei numeri con la notazione scientifica basata sulle potenze di 10 ti consiglio di prestare molta
attenzione al fatto che il numero sia molto grande o molto piccolo;
2.
Se devi eseguire un’equivalenza pensa sempre alla corrispondenza biunivoca che c’è fra il prefisso delle unità
di misura del Sistema Internazionale e la potenza di 10 corrispondente;
3.
Utilizzare le potenze di 10 ti sembrerà all’inizio difficile, ma se ti impratichisci un po’ ne apprezzerai i vantaggi
dati dalla loro forma concisa e dalla semplicità con cui si possono eseguire i calcoli.
Esercizi proposti
1. Scrivi in notazione scientifica la distanza tra la Terra e il Sole = 149,57 milioni di km e trasforma il risultato in
metri.
2. Esprimi in metri, usando la notazione scientifica, la misura del raggio dell’atomo d’idrogeno = 0,5
decimilionesimi di mm.
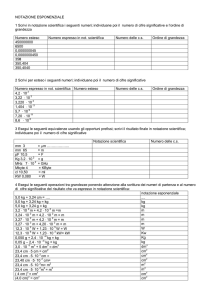
3. Completa la seguente tabella svolgendo l’equivalenza indicata e scrivi il numero in notazione scientifica:
0,012g
kg
18 000 cm
m
72 800 kHz
Hz
0,000041 ms
248 mg
178 m
0,000021 s
85 320 000 W
19 000 miliardi di m
s
kg
mm
µs
MW
Tm
6 425 g
kg
505 nF
F
Consigli:
Per determinare l’ordine di grandezza del risultato di una misura è opportuno seguire le azioni:
1. Scrivi la misura in notazione scientifica utilizzando le potenze di 10 e “traducendo” anche in potenza di 10
l’eventuale prefisso dell’unità di misura.
2. Fa’ l’opportuna equivalenza all’unità di misura se non è del Sistema Internazionale.
3. Esegui i calcoli con le potenze di 10 e approssima opportunamente il coefficiente.
4. Determina l’ordine di grandezza.