TEORIA DEL PRODUTTORE
10/15
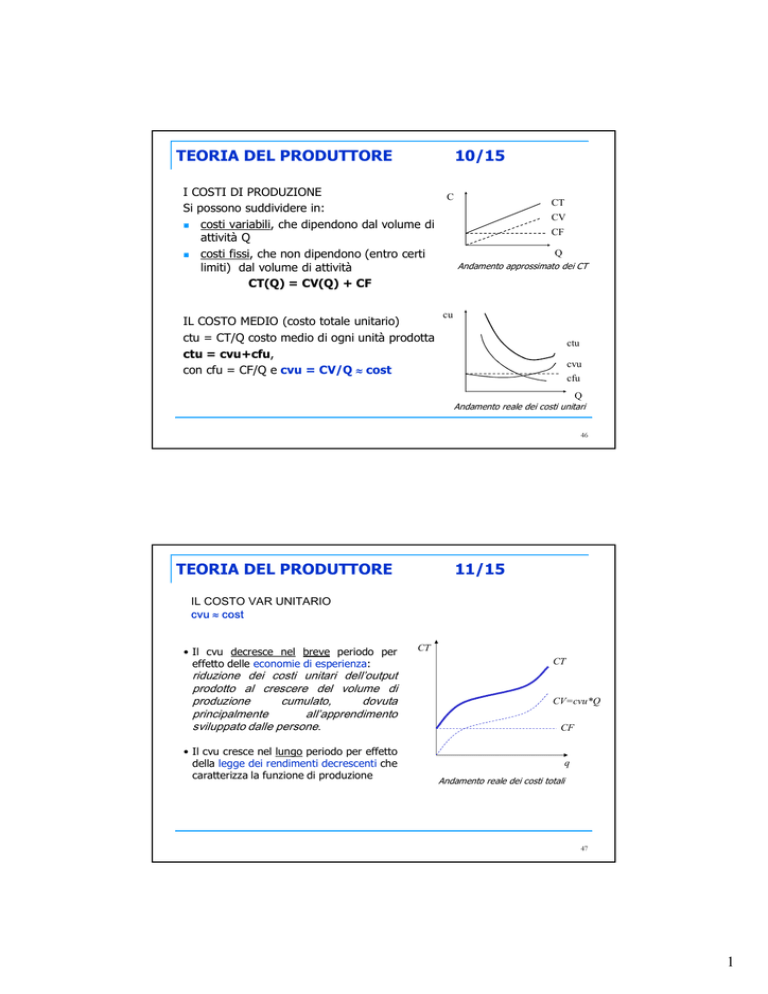
I COSTI DI PRODUZIONE
Si possono suddividere in:
costi variabili, che dipendono dal volume di
attività Q
costi fissi, che non dipendono (entro certi
limiti) dal volume di attività
CT(Q) = CV(Q) + CF
IL COSTO MEDIO (costo totale unitario)
ctu = CT/Q costo medio di ogni unità prodotta
ctu = cvu+cfu,
con cfu = CF/Q e cvu = CV/Q cost
C
CT
CV
CF
Q
Andamento approssimato dei CT
cu
ctu
cvu
cfu
Q
Andamento reale dei costi unitari
46
TEORIA DEL PRODUTTORE
11/15
IL COSTO VAR UNITARIO
cvu cost
• Il cvu decresce nel breve periodo per
effetto delle economie di esperienza:
riduzione dei costi unitari dell’output
prodotto al crescere del volume di
produzione
cumulato,
dovuta
principalmente
all’apprendimento
sviluppato dalle persone.
• Il cvu cresce nel lungo periodo per effetto
della legge dei rendimenti decrescenti che
caratterizza la funzione di produzione
CT
CT
CV=cvu*Q
CF
Andamento reale dei costi totali
q
47
1
TEORIA DEL PRODUTTORE: un esempio
Q
0
1
2
3
4
5
6
CF
55
55
55
55
55
55
55
I costi al variare del livello di attività
CV CT=CF+CV
0
55
30
85
55
110
75
130
105
160
155
210
225
280
300
c
280
250
210
200
150
100
55
50
0
0
130
110
85
160
105
75
55
30
0
1
2
225
155
3
4
5
Q 6
48
TEORIA DEL PRODUTTORE: un esempio
Q
0
1
2
3
4
5
6
CF
55
55
55
55
55
55
55
CV
0
30
55
75
105
155
225
CT
55
85
110
130
160
210
280
cf=CF/Q
55,0
27,5
18,3
13,8
11,0
9,2
cv=CV/Q
30,0
27,5
25,0
26,3
31,0
37,5
ctu=CT/Q
85,0
55,0
43,3
40,0
42,0
46,7
i costi medi al variare della quantità prodotta
90
80
70
60
50
40
30
20
10
0
0
1
2
cf=CF/Q -
3
4
cv=CV/Q -
5
6
7
ctu=CT/Q -
49
2
TEORIA DEL PRODUTTORE
12/15
IL COSTO MARGINALE
Costo aggiuntivo sostenuto per produrre una unità addizionale di output:
Cma= CT/Q (=CV/Q)
graficamente è dato dalla pendenza della curva del costo totale
Q
0
1
2
3
4
5
6
CT
55
85
110
130
160
210
280
costo medio e marginale
Cma
30
25
20
30
50
70
300
250
200
150
100
50
0
0
1
2
3
4
Cma -
TEORIA DEL PRODUTTORE
5
CT
6
7
50
13/15
IL COSTO MARGINALE
Cma= CT/Q (=CV/Q)
C
RELAZIONE TRA CT ctu Cma
Cma = CT = (ctuxQ) = ctu xQ + ctu
Q
Q
Q
se ctu = min ctu x Q =0
Q
x
ctu = Cma
Cma
Cma = CT = CV = (cvuxQ) = cvu xQ + cvu x Q
Q
Q
Q
se cvu = min cvu x Q =0
Q
Q
CV
CF
Q
Q
CT
Q
Q
Q
cvu = Cma
51
3
TEORIA DEL PRODUTTORE
14/15
RELAZIONE TRA CT ctu Cma
se ctu = min ctu = Cma
se cvu = min cvu = Cma
Se Cma= min CT min pendenza
cu
Minimo costo totale unitario
Cma
ctu
cvu
Minimo costo variabile unitario
Q
52
TEORIA DEL PRODUTTORE
15/15
LA MASSIMIZZAZIONE DEL PROFITTO
Obiettivo dell’Impresa è massimizzare il profitto: P(Q) = R(Q) – CT(Q)
P(Q) = max
se dP(Q) / dQ = 0
dR(Q)/dQ – dCT(Q)/dQ = 0
Qottima = Q tale che
Rma – Cma = 0
Rma(Q) = Cma(Q)
esercizi
53
4
La relazione tra le curve di ctu di breve e di lungo periodo
Si supponga che un’impresa stia considerando di aumentare il volume di
attività aumentando il capitale (es. acquistando nuovi macchinari o
ampliando lo spazio produttivo).
L’impresa ha allora due
funzioni di produzione di
breve periodo e due
corrispondenti funzioni di
costo di breve periodo
A seconda del livello di produzione ci sarà una curva di CTU più
bassa, ovvero un livello di capitale che assicura minimo costo
54
La curva di ctu nel lungo periodo
Immaginando di considerare
tutti i livello di capitale possibili,
si otterrà una curva di CTUBP
per ogni livello di capitale
C
CTUBP1
CTUBP2
CTUBP3
CTUBP4
CTULP
Q
La curva di CTU di lungo periodo si genera utilizzando i tratti
più bassi delle curve dei CTU di breve periodo
55
5
IL MERCATO DI CONCORRENZA PERFETTA 1/5
CARATTERISTICHE
Il prodotto offerto è
omogeneo
Pluralità di imprese
Domanda e offerta
assumono il prezzo
come un vincolo
(esiste perfetta
sostituibilità fra i beni
offerti dalle imprese)
Libertà di accesso ai
fattori produttivi
Libertà di ingresso e
di uscita dal
mercato
56
IL MERCATO DI CONCORRENZA PERFETTA 2/5
CURVA DI DOMANDA INDIVIDUALE NEL MERCATO CONCORRENZIALE
La quantità prodotta da una impresa nel mercato è irrilevante rispetto alla
quantità complessiva offerta da tutti i produttori del mercato
La curva di domanda individuale è orizzontale: q(p) = Q(p) / n.produttori
il prezzo del bene non è modificabile dal singolo produttore
Il ricavo dell’impresa è R(q) = p x q, poiché p(q)=costante
p
p
Curva di
domanda
del mercato
Q
Curva di
domanda
dell’impresa
R
q
Ricavi
dell’impresa
Rm = p
R=pxq
q
57
6
L’EQUILIBRIO IN CONCORRENZA PERFETTA 3/5
Problema della dimensione ottima del volume di produzione, noti il
prezzo di mercato e i costi di produzione:
Obiettivo: max profitto Л, noti CT(Q) e p di mercato
Л = ricavi - costi tot. = pQ - CT = max
Rma = Cma
p = CT/Q
p,c
Cma
se Л / Q = 0
p = Cma (Q)
Q ottima
p(q)
q
Qott
58
L’EQUILIBRIO IN CONCORRENZA PERFETTA 4/5
Qual è il MAX PROFITTO, corrispondente a Qott?
p,c
•Se p=Cma > ctu allora
l’impresa realizza Л>0
(PROFITTO)
Cma
ctu
Л = (p-ctu)xQ
Qott
p(q)
•Se p < ctu allora l’impresa
realizza Л<0 (PERDITA)
q
P(q)
Punto di pareggio
Cma
ctu
q
59
7
L’EQUILIBRIO IN CONCORRENZA PERFETTA 4bis/5
Nel breve periodo l’impresa continua a
produrre anche se p < ctu (in perdita)
fintanto che p > cvu
➪ con I ricavi copre i cvu e una parte
dei CF
➪ I CF permangono anche se q=0
OFFERTA
INDIVIDUALE
cu
Cma
ctu
Punto di
chiusura
q t.c. p = Cma(q)
q=0
cvu
Q
se p > cvu
se p < cvu
60
L’EQUILIBRIO DI LUNGO PERIODO
IN CONCORRENZA PERFETTA 5/5
IPOTESI: libertà di ingresso e di uscita delle imprese dal mercato
Se le imprese presenti nel mercato realizzano Л >0 nel lungo
periodo nuove imprese entrano nel mercato diminuendo il profitto di
ogni impresa
Se le imprese presenti nel mercato realizzano Л <0 nel lungo
periodo usciranno delle imprese dal mercato aumentando il profitto
delle imprese rimanenti
Il processo di entrata ed uscita termina quando le imprese nel
mercato realizzano Л = 0 ⇨ p = Cma = ctu
61
8
SINTESI: scelta del livello di produzione
Tecnologia e costi
dei fattori produttivi
Cma
Curva di domanda
•è opportuno
produrre nel BP?
•è opportuno
chiudere nel LP?
CT e ctu
(BT e LTP)
Ricavo
unitario
Rma
Q ottima di produzione
breve termine Q ottima è t.c. Rma = Cma di BT
lungo termine Q ottima è t.c. Rma = Cma di LT
P > cvu
P > ctu
Ripasso: i costi
di produzione
Cma
RELAZIONI:
se ctu = min ctu = Cma
se cvu = min cvu = Cma
ctu
cvu
cfu
63
9
ESERCIZI
Data la seguente funzione dei costi totali di un’impresa:
CT=7Q+220Q2, si calcolino le seguenti funzioni di costo: Cme, Cvu, Cma,
CFtotale, CVtotale.
- nel caso in cui costi fissi totali CF=880 si aggiungano alla funzione di CT,
ripetere l’esercizio e verificare la relazione che lega il Cma e il Cme.
Un’impresa che opera in un mercato in concorrenza perfetta
prodotto che realizza al prezzo unitario di 0.10€. Il suo costo
produzione è CT=65-0.5q+0.001q2. Si determini la quantità che
deve produrre per massimizzare il proprio profitto e il profitto
ottenibile.
vende il
totale di
l’impresa
massimo
Nel settore dell’olio di semi sono presenti 100 imprese dalle caratteristiche
identiche, la cui curva dei costi marginali è rappresentata da Cma=10+q. La
domanda del settore è p=30- 3Q/100.
a) quanto olio [barili] sarà prodotto dal settore e dalla singola impresa?
b) a quale prezzo [€]?
64
65
10
IL MERCATO DI MONOPOLIO
1/3
Il mercato di monopolio si caratterizza per la presenza di un unico
produttore
LE RAGIONI DEL MONOPOLIO
Ragioni
Ragioni
–
–
legali: concessioni governative, presenza di brevetti, copyright
economiche:
quando la struttura dei costi di produzione rende la singola
impresa più efficiente di una molteplicità di produttori (settori
economici caratterizzati da elevate economie di scala)
quando una risorsa chiave è detenuta o controllata da un’unica
impresa
66
IL MERCATO DI MONOPOLIO
2/3
CURVA DI DOMANDA NEL MERCATO IN MONOPOLIO
Il monopolio è caratterizzato dall’offerta di un bene per il quale non
esistono sostituti
Il monopolista riesce pertanto a controllare il prezzo del bene offerto e
si confronta direttamente con la curva di domanda del mercato:
qd(p)
all’impresa
= Qd(p)
sul mercato
p
R(Q)
Curva di
domanda
Curva dei
ricavi tot.
CT
Q
Qott
RT
Q
67
11
L’EQUILIBRIO IN REGIME DI MONOPOLIO 3/3
L’imprenditore può determinare il prezzo di mercato, ma deve
confrontarsi con la curva di domanda
Problema della dimensione ottima del volume di produzione, noti i costi
di produzione e la domanda di mercato:
Obiettivo: max profitto Л, noti CT(Q) e la domanda di mercato p=p(Q)
Л = ricavi - costi tot. = max se Л / Q = 0
Rma(Q) = Cma(Q)
R/Q=CT/Q
p
R(Q)
Curva di
domanda
Curva dei
ricavi totali
RT
Q
Rma
CT
Qott
Q
Cma
Q
Qottima
LE PRINCIPALI FORME DI MERCATO
68
Concorrenza
perfetta
Monopolio
assoluto
Oligopolio
Caratteristiche
del prodotto
omogeneo
unico
Chi determina il
prezzo
Omogeneo o
poco
eterogeneo
mercato
venditore
venditori
venditori, con
molte limitazioni
libero
impedito
impedito
libero
frequente
molto frequente
Acciaio, pr.
Chimici,
automobili,
produttori sw
Commercio al
dettaglio:
benzina, PC,
ristoranti,..
N. di venditori
Accesso di nuove
imprese
Frequenza
esempi
molti
raro
Mercati
finanziari e
alcuni prodotti
agricoli
(carote)
uno
raro per
imprese
private
Fornitori
locali di
public utilities
pochi
Concorrenza
monopolistica
molti
eterogeneo
69
12
ESERCIZIO 1
Un’impresa che opera in un mercato in monopolio ha la seguente funzione
dei costi totali: CT=Q2 /1000. La curva di domanda di mercato per il bene
prodotto dall’impresa è Q=4000-1000p. Si calcoli:
a) il prezzo e la quantità prodotta nelle condizioni di equilibrio
b) il profitto realizzato dal monopolista
c) la quantità offerta dalle imprese qualora il mercato fosse di concorrenza
perfetta, supponendo che il costo marginale rimanga invariato.
70
ESERCIZIO 3
L’impresa Orazio produce beni utilizzando una tecnologia descritta dalla
seguente funzione di produzione: q = L1/2 K1/2 . I prezzi dei fattori lavoro L e
capitale K risultano rispettivamente pari a pL= 25, e pK = 16.
a) Si supponga che l’impresa abbia deciso di produrre una quantità di output
pari a q = 20. Si determini la combinazione ottimale di lavoro e capitale che
minimizza il costo di tale produzione.
b) Si supponga che l’impresa abbia deciso di volere spendere al massimo C =
1600 nel processo produttivo. Si determini la combinazione ottimale di lavoro
e capitale che permette di massimizzare la produzione dato il vincolo di
spesa.
c) Si supponga che nel breve periodo la dotazione di capitale a disposizione dell’
impresa sia costante e pari a K = 9. Si determinino le funzioni di breve
periodo di costo totale, medio e marginale.
71
13
ESERCIZIO 4
Si consideri un mercato perfettamente concorrenziale in cui operano 40 imprese
identiche, la cui funzione di costo è C = q2 + 16. La curva di domanda del
mercato in cui operano le imprese è data da Qd = 180 - 10p.
(a) Si determini la curva di offerta di breve periodo di ciascuna impresa.
(b) Si determini la curva di offerta di breve periodo del mercato, la quantità e il
prezzo di equilibrio.
(c) Si calcoli la produzione di equilibrio delle singole imprese nel breve periodo e
i prodotti conseguiti.
(d) Si calcoli la quantità prodotta e il numero di imprese operanti sul mercato nel
lungo periodo.
72
14










