Esperimenti e modelli in ottica fisica per l’innovazione
didattica e la formazione degli insegnanti
M. Michelini, A. Stefanel, L. Santi,
Unità di Ricerca in Didattica della Fisica dell'Università di Udine
Introduzione
L’ influenza delle Tecnologie dell’Informazione e della
Comunicazione (TIC) determina nuovi modi di guardare, acquisire
informazioni, apprendere: ad esempio si ha facilità nel cogliere
correlazioni e nel guardare contemporaneamente ad aspetti diversi,
mentre è più difficile approfondire aspetti specifici. Ciò pone un
problema formativo a cui si affianca la necessità di rinnovamento del
modo di fare scuola e organizzare la didattica (Caravita, Hallden 1995).
All’insegnante é richiesta una nuova professionalità, che consiste in un
complesso insieme di abilità e di conoscenze non solo disciplinari, ma
anche tecniche, pedagogiche, sociali e organizzative (Eraut 1994;
Marucci et al. 2001; Michelini 2003). Al suo ruolo di mediatore
culturale, tutor e di organizzatore di autonomi processi cognitivi va
aggiunto quello di creatore di “ambienti di apprendimento”, che
permettano di pianificare e di condurre un’articolata e complessa rete di
attività, in grado di promuovere coerenti percorsi di apprendimento
personalizzati (Linder et a. 1997). Per gli insegnanti di fisica, in
particolare, l’impegno innovativo richiesto è maggiore, perché le ICT
rendono possibili obiettivi formativi ed esperienze nella didattica finora
dominio della sola ricerca. Le ICT costituiscono inoltre potenti strumenti
educativi per affrontare i nodi disciplinari, favorire il superamento delle
difficoltà di apprendimento, innescare risonanza tra metodologie
didattiche e metodologie proprie della disciplina (Riel 1998; Swan,
Miltrani 1998). Misure con sensori on-line e modellizzazione al
computer aprono la strada al vaglio di ipotesi interpretative formalizzate
ed all’indagine di coerenza tra le conseguenze delle ipotesi e i dati
sperimentali.
Diversi studi (Sander et al. 1996; Anderson 1995; Michelini,
Pugliese 1999: Buchberger et al. 2000; Michelini 2001) hanno chiarito,
che per produrre competenti e qualificate innovazioni, é necessario
promuovere una formazione degli insegnanti sostenuta dalla ricerca,
integrando modalità differenziate: metaculturali, esperienziali, situate
1
(Linder et al 1997; Michelini 2003). Sono necessarie proposte operative
(Michelini, Pugliese, 1999; Bosio, Di Pierro et al. 1999; Pugliese,
Michelini 2001; Michelini, Santi 2001), in grado di dare risposta ai
bisogni formativi degli insegnanti (Pugliese Jona et al. 1999; Michelini,
Mossenta 2001), far superare la generale tendenza a trasformare
proposte innovative riproponendo stili di insegnamento tradizionali (Day
et al. 1990; Pintò et al. 2001). É necessario, inoltre, il supporto di
specifici e dettagliati materiali (Aiello et al. 1997), strumenti per la
progettazione e la conduzione dell’attività in classe (Marucci et al. 2001;
Martongelli et al . 2001), in grado di promuovere nuove strategie
formative, nuovi modi di interagire con i ragazzi (Anderson 1995;
Sander et al. 1996 Swan, Miltrani 1998; Michelini 2001).
Nell’ambito di una collaborazione nazionale di ricerca1 é stato
studiato particolarmente il problema della formazione insegnanti in
fisica e il contributo delle TIC, mettendo a punto un protocollo di
sperimentazione (Aiello et al. 1997) e un modello per la formazione
insegnanti in presenza e a distanza (Sperandeo 2001). Particolarmente
significativi sono stati i Moduli di Intervento Formativo (MIF)
sperimentati sia nella formazione iniziale, sia nella formazione in
servizio degli insegnanti. L’Unità di Udine ha prodotto in questo
contesto diversi ambienti di proposte didattiche per gli insegnanti,
pubblicati in rete telematica [www.fisica.uniud.it/URDF/].
Un ambiente sull’ottica fisica è in particolare pensato come
cuscino culturale per la transizione dalla fisica classica a quella
quantistica. Esso viene presentato in questa sede (fig. 1) (Michelini,
Santi, Stefanel 2002; Cobal, Corni, Michelini, Santi, Stefanel 2002),
come percorso attraverso esperimenti, che impiegano sensori on line con
il computer, materiali e strumenti didattici validati nell’ambito di
sperimentazioni pilota, che hanno coinvolto anche gli specializzandi
della Scuola di Specializzazione all’Insegnamento Secondario di Udine
(Michelini et al. 2004).
Si illustrano in particolare le modalità di presentazione dei
materiali, le motivazioni e le scelte di impostazione per la intera
proposta di ottica fisica, le proposte sperimentali e un percorso per
ciascuna delle tre direttrici principali individuate: produzione e
assorbimento di radiazione luminosa; diffrazione e interferenza,
polarizzazione.
2
Fig. 1 La home-page del cuscino di ottica fisica del Progetto SeCiF
Valenze culturali e didattiche dell’ottica fisica
Esplorare fenomeni di interazione tra la radiazione e la materia,
per riconoscerne gli aspetti peculiari, caratterizzarli mediante le
intrinseche proprietà e interpretarle sulla base di modelli costituisce in sé
un'esperienza formativa così ricca da potersi proporre come contenuto
irrinunciabile per un curriculum (Pereira et al. 1993). Il passaggio dalla
descrizione dei fenomeni all’interpretazione in termini di modelli, oltre
ad avere rilevanza storica (Gonzales 1993), gioca anche un ruolo di
ponte, da un lato tra l’ottica geometrica e l'elettromagnetismo classico e
dall’altro tra la meccanica classica e quella quantistica (Bradley etr al.
1999, Ghirardi et al. 1995, 1997; Pospiech 2000; Holbrow et al. 2002;
Cobal, Corni, Michelini 2002; Schneider, La Puma 2002; Michelini
2003). L’ottica fisica trova, inoltre, ampio impiego in numerosi campi:
3
medico (ne sono esempio le numerose applicazioni del laser),
tecnologico
(cristallografia),
nella
scienza
dei
materiali
(caratterizzazione di proprietà; interferometria; nuovi materiali
polimerici), biologico (visione polarizzata).
Per la didattica vi possono essere vari approcci ai fenomeni
ottici: da un lato molti oggetti di uso comune costituiscono applicazioni
tecnologiche dell’ottica fisica, che possono essere usate come oggetti di
studio (Hudoba 1996) o possono essere utilizzate per costruire semplici
proposte sperimentali (O’Connell 1999; Moloney 1999; Beneson 2000;
Chaudhry e Morris 2000; Mirò, Pitò 2001; Colin, Rodriguez 2002;
Hernadez-Andres et al. 2002; Wheleer 2004), dall’altro sensori collegati
in linea con l’elaboratore offrono nuove opportunità di apprendimento in
questo campo soprattutto in merito ai fenomeni di interazione lucemateria (Hirata 1986; Bunch 1990; Giugliarelli et al. 1994; Michelini
1999; Ouseph 1999; Easton 2001; Hinrichsen, 2001; Chauvat et al.
2003; Grove 2003). Sistemi di misura e modellizzazione per la didattica
basati sull'elaboratore consentono di aprire un mondo di potenzialità
interpretative, attuare strategie, che valorizzano il contributo formativo
sul piano sperimentale e interpretativo dell’ottica fisica, troppo spesso
trascurato nella pratica didattica in cui, per esempio, la polarizzazione
della luce non viene quasi mai affrontata e il fenomeno della diffrazione
viene trattato in modo solo semiquantitativo, con una semplice analisi
della posizione di massimi e minimi di intensità luminosa nella figura di
diffrazione (Mascellani et al. 1992; Corni et al 1993; Santi et al. 1993;
Wosilait et al. 1999; Cobal et al 2002).
Tali strategie permettono di affrontare i principali nodi
disciplinari e superare le difficoltà di apprendimento connesse, in primo
luogo, all’utilizzo contemporaneo del modello ondulatorio e di quello
corpuscolare, in contesti dove quest’ultimo non é più evidentemente
applicabile (Bradley etr al. 1999), al mancato riconoscimento dei
processi di emissione di luce (Mirò, Pintò 2001).
Materiali per insegnanti di una proposta didattica in ottica fisica
Le nostre proposte sull’ottica fisica per gli insegnanti si sono
tradotte in materiali differenziati redatti in forma ipertestuale in
ambiente web nell’ambito del progetto SeCiF1. Le caratteristiche dei
materiali sono studiate, in modo che questi possano essere offerti come
ponte culturale per la transizione tra la fisica classica e la meccanica
4
quantistica. Al tempo stesso si prestano ad essere utilizzati come unità di
lavoro autonome, trattate a differenti livelli, con un formalismo
semplice. L’organizzazione dei materiali prodotti per il progetto SeCiF
si richiama alla metafora dell’esplorazione di un territorio. Per fornire
indicazioni all’insegnante sulle scelte fatte, vengono presentate
l’impostazione disciplinare, l’approccio didattico seguito per affrontare
la tematica, la strategia e metodi utilizzati nella proposta didattica. La
presentazione del percorso didattico proposto (il filo) viene preceduta
dai prerequisiti richiesti e dalle mappe, che illustrano l’intero panorama
dei fenomeni ottici considerati. Due altre mappe sono dedicate
all’organizzazione delle proposte sulla diffrazione e sulla polarizzazione.
Una serie di materiali a supporto della formazione culturale
dell’insegnante e del suo lavoro di progettazione (caratteri
interdisciplinari) correda la proposta. Vi sono in essa indicazioni su
agganci interdisciplinari, per esempio in ambito biologico,
cristallografico, tecnologico. Nelle risorse sono disponibili tre contributi
dal titolo: 1) la polarizzazione della luce: osservazioni e modelli; 2) la
birifrangenza; 3) la polarizzazione: immagini in rete. La prima analizza
la polarizzazione a partire dalla natura elettromagnetica della luce. Ne
evidenzia le caratteristiche e attraverso semplici modelli rende conto dei
principali fenomeni. La seconda consiste nella presentazione
dell’utilizzo della polarizzazione in cristallografia. La terza propone una
selezione di immagini in rete, utili per fornire una panoramica iniziale
sul fenomeno della polarizzazione e alcune sue applicazioni.
Una discussione dei contenuti si collega alla presentazione del
filo e a quella degli esperimenti, in cui rispettivamente si illustrano il
percorso didattico e gli esperimenti su cui esso si basa, con dettagliata
illustrazione delle attività proposte e dati campione. Si tratta di learning
object, utilizzabili in contesti differenziati2.
Alcune simulazioni permettono di ripercorrere il processo
interpretativo dei fenomeni più complessi, come la diffrazione.
Documentazioni sulle sperimentazioni effettuate in classe
completano la presentazione dei materiali.
Le scelte e l’impostazione della proposta didattica in ottica fisica
Nella nostra proposta viene considerata la principale
fenomenologia dell'ottica fisica, scegliendo quelle situazioni e quegli
aspetti, che hanno costituito elementi di crisi dal punto di vista
5
interpretativo per l'ottica geometrica in prima istanza e per quella
elettromagnetica a un livello più elevato (Cobal, Corni, Michelini, Santi,
Stefanel 2002). Due obiettivi principali sottendono la proposta: 1)
familiarizzazione con la fenomenologia, offrendo esperienza di analisi di
semplici casi di emissione ed assorbimento di luce nell'esperienza
quotidiana, di misure di interferenza e diffrazione, di riconoscimento
proprietà di polarizzazione della luce; 2) guadagnare esperienza delle
problematiche connesse al processo di analisi interpretativa della
fenomenologia, imparando ad argomentare le ipotesi e a sostenerle sul
piano quantitativo o semiquantitativo, con attività di modellizzazione al
computer (computer modelling).
Strategie e metodi fanno riferimento al ciclo (EPSI):
Esplorazione di fenomeni comuni - costruzione di ipotesi (Previsioni)indagine Sperimentale – formulazione di Interpretazioni da estendere ad
altri campi fenomenologici. Si suggerisce che gli studenti costruiscano
ipotesi avendo modelli interpretativi come referenti concettuali e
progettino misure i cui esiti possano venire confrontati con le ipotesi
interpretative.
Fig. 2 La mappa generale sull’ottica fisica.
6
Il percorso presuppone lo studio dei principali fenomeni di
propagazione della luce e la loro interpretazione nel quadro dell'ottica
geometrica. Si assume familiare anche la fenomenologia della rifrazione,
benché non completamente interpretata. L'elettromagnetismo classico
non costituisce conoscenza propedeutica, come del resto storicamente è
avvenuto.
Tre mappe relative all’intero cuscino di ottica, alla proposta sulla
diffrazione ed a quella sulla polarizzazione presentano il territorio
dell’impostazione culturale a cui fanno riferimento i materiali e le
proposte didattiche, pubblicate in ambiente web (fig. 2).
La proposta di ottica fisica si sviluppa a partire da tre nodi:
1)
la propagazione della luce che incontra ostacoli: la luce
che attraversa una finestra, una fenditura, un bordo, un filo e i processi
di interferenza e diffrazione che propongono il passaggio interpretativo
dall’ottica geometrica a quella fisica3;
2)
l’interazione della luce con materiali diversi: riflettività,
assorbimento, trasmissione e selezione cromatica dei materiali: i primi
passi per correlare le proprietà ottiche ed elettriche dei materiali;
3)
le sorgenti di luce: i processi energetici associati, intensità
luminosa e sua possibile interpretazione con l’idea di fotone.
L’esplorazione dei fenomeni di interazione della luce con la
materia, posta su basi semiquantitative, avvia ad una rilettura di
fenomeni quotidiani come riflessione, rifrazione e assorbimento. In
questo contesto si affronta la diffrazione mediante misure di
distribuzioni di intensità luminosa prodotte da fenditure ed ostacoli,
effettuate con sensori in linea con l’elaboratore. Si considera il fronte
d'onda incidente sulla fenditura diffrangente costituito da un numero
crescente di polaroid. Mediante un’attività di computer modelling e/o di
simulazione si calcolano le distribuzioni di intensità da esse prodotte. Gli
esiti sperimentali si confrontano con quelli del calcolo. L'interazione
della luce con la materia viene proposta in termini quantitativi con
analisi energetiche legate a processi di assorbimento della luce solare e
di quella prodotta da sorgenti incandescenti (lampadine a filamento).
L'emissione di luce da parte di una lampadina viene proposta come
occasione per comprendere i principali processi energetici coinvolti
nell'emissione di luce da parte di corpi incandescenti. Sensori in linea
con l'elaboratore sostengono ancora una volta l'esplorazione delle
caratteristiche con cui varia l'intensità luminosa della luce, che attraversa
7
vari tipi di filtri e anche l'analisi energetica che caratterizza la variazione
di energia interna di sistemi che assorbono luce. Sempre nel quadro dei
processi di interazione luce materia, si riconosce la polarizzazione come
proprietà della luce, che può essere simultaneamente descritta da un
vettore in quadri interpretativi profondamente diversi. La proposta sulla
polarizzazione suggerisce piani di lettura diversi: interpretazione di
processi su base fenomenologica (leggi di Malus e Brewster),
produzione e applicazioni di luce polarizzata, significato della natura
probabilistica dei fenomeni e concetto di stato di un fotone, attraverso lo
studio delle “proprietà” che ad esso possono essere associate in base agli
esiti sperimentali. Strategie e metodi propongono l’esplorazione di
fenomeni comuni e la loro caratterizzazione, come punto di partenza per
porsi domande e costruire ipotesi, istruire indagini sperimentali e
pianificare interpretazioni, spesso attraverso l’uso di strumenti di
simulazione e modellizzazione, che permettano di porre a confronto esiti
sperimentali con modelli.
Interazione luce materia: emissione e assorbimento
L'emissione di luce e l'energia ad essa associata sono proposte in
termini di studio esplorativo sperimentale in una prima fase (Bosio,
Michelini, Santi 1996, 1999; Bosio, Michelini, 1997). L'analisi
dell'emissione di luce da parte di un filamento di lampadina ad
incandescenza, viene proposto come caso per lo studio delle
caratteristiche di una sorgente luminosa.
Con il dispositivo che realizza lo schema illustrato nella figura 3
si effettua l’analisi della curva caratterista V=V(I) della lampadina (fig.
4). Essa porta alle seguenti considerazioni:
1. nella regione strettamente ohmica, a basse temperature,
possiamo ritenere che tutta la potenza elettrica venga dissipata per la
conduzione;
2. aumentando il lavoro elettrico fornito alla lampadina, una
parte di questo viene utilizzata per il riscaldamento del filo ed un’altra,
sempre più consistente, viene dissipata verso l’esterno sotto forma di
energia radiante. Al crescere della temperatura del filamento le
caratteristiche dell’irraggiamento si modificano progressivamente sia per
l’importanza assunta da tale contributo dispersivo nel bilancio
energetico che per il cambiamento del colore della radiazione emessa, e
cioè della lunghezza d’onda per la quale l’emissione si caratterizza;
8
3. Ad un certo punto si può ritenere che l’irraggiamento prevalga
su tutti gli altri contributi dissipativi. Si stabilisce allora una condizione
di equilibrio termico dinamico, in cui tutta l’energia fornita al sistema
viene emessa sotto forma di radiazione elettromagnetica.
Fig. 3 Schema del dispositivo per la misura delle caratteristiche V=V(I) della
lampadina. La corrente I, che circola nel filamento della lampadina, viene ricavata
dalla relazione I=V’/ Rn. Si effettua la misura della tensione V’ ai capi di un
resistore di valore noto Rn posto in serie alla lampadina, ottenendo in questo modo
misure affidabili anche a basse tensioni e una valutazione attendibile della
resistenza Ro del filamento a temperatura ambiente.
Nella curva descritta dai dati in figura 4 vi sono due cambiamenti
di pendenza. Il primo è facilmente riconoscibile e rappresenta la
transizione dalla regione ohmica a quella in cui l’irraggiamento acquista
un ruolo significativo nel bilancio energetico.
La transizione da quest’ultima alla regione in cui tutta l’energia
viene dissipata per irraggiamento non è altrettanto netta, anche se da un
certo valore della potenza in ingresso si può considerare che essa sia
tutta utilizzata per l’irraggiamento..
Si determina la temperatura T del filamento in due modi:
mediante la legge che governa la dipendenza da essa della resistenza,
9
note le proprietà elettriche del conduttore, e mediante la legge di StefanBoltzmann.
Fig. 4 Caratteristiche V= V(I) della lampadina.
Il primo metodo si basa sul fatto che, il filamento è di tungsteno, un
metallo che presenta una dipendenza superlineare della resistività dalla
temperatura T, di tipo:
T 1.2.
La resistenza del filamento è determinata anche dalle sue
caratteristiche geometriche, secondo la ben nota relazione R = l / S,
con l e S lunghezza e sezione del filamento, rispettivamente. La
dipendenza di R dalla temperatura è perciò sostanzialmente quella di
Sostituendo si ottiene:
T = To (R / Ro) 1/ 1.2 ,
con Ro resistenza del filamento della lampadina a temperatura
ambiente To. Già per valori della tensione elettrica di qualche Volt è
lecito assumere che il contributo dell’irraggiamento alla dissipazione
dell’energia fornita al sistema prevalga su quelli dovuti a conduzione e
convezione, perciò la potenza elettrica fornita si può considerare
corrispondente a quella emessa:
P (in) = P (emiss),
10
dove P (in) = V*I, con V tensione ai capi del filamento e I
corrente elettrica che circola in esso.
Il secondo metodo utilizza la legge di Stefan-Boltzmann, per la
quale si ha:
P(emiss) = A (T 4 - T0 4),
dove è la costante di Stefan Boltzmann, A è la superficie
emittente del filamento e è l’emissività del tungsteno, che si assume
pari a 0.32, trascurandone in prima approssimazione la sua dipendenza
dalla temperatura. Si ottiene quindi l’espressione:
P (in) = V I = P (emiss) = A (T 4 - T0 4) A T 4 ,
dove nell’ultimo passaggio si è utilizzato il fatto che senz’altro T
>> T0 . Il precedente risultato fornisce una seconda relazione utile per la
determinazione della temperatura T:
T (V I / A ) ¼.
Se si trascurano gli effetti di autoaffacciamento dovuti alla
spiralizzazione del filamento, che del resto nelle lampadine da bicicletta
non è molto accentuata, si può esprimere A in funzione della lunghezza
L e del diametro d del filamento assimilando quest’ultimo ad un
cilindro. Si ottiene così la seguente relazione:
T ( (V I ) / ( L d) ) 1/4
Le misure di temperatura ricavate con i due metodi sono
coerenti, anche se quelli ottenuti dalla dalla legge di Stefan risultano
sistematicamente superiori con uno scarto medio del 15 % . Tale scarto
evidenzia i limiti del modello semplificato adottato, che trascura la
dipendenza dell’emissività dalla temperatura e il ruolo della
spiralizzazione del filamento.
La prima fase di esplorazione dell'interazione della luce con la
materia si conclude con l'esame di processi di assorbimento (Michelini,
Pascoli 1997 a, b).
Nel percorso proposto si caratterizza dal punto di vista energetico
il processo di emissione, misurando la percentuale di luce visibile
emessa dalla lampadina per via calorimetrica.
Il modo in cui viene trasportata l'energia dalla luce viene
indagato riconoscendo sperimentalmente la legge di dipendenza
dell'illuminamento con il quadrato della distanza dalla sorgente.
11
L'energia assorbita da piastrine metalliche di diversa superficie e
spessore, da provette colorate esposte alla luce solare o di una lampada
permette di riconoscere i fattori che influenzano l'assorbimento di luce.
Nella Tabella 1 sono riportate le attività sperimentali attraverso
cui si sviluppa il percorso. Si tratta per lo più di esperienze semplici, alla
portata di ragazzi di 14-16 anni, che vengono suggerite mediante
l’impiego di sensori collegati in linea con il computer. Richiedono come
prerequisiti una certa padronanza nell'analisi di bilanci energetici e nel
loro studio sperimentale, la comprensione della distinzione tra energia
scambiata e potenza.
Emissione di luce da una lampadina
1. Temperatura del filamento incandescente
2. Efficienza luminosa della lampadina da bicicletta
3. Dipendenza dell'illuminamento dalla distanza
4. Dipendenza della resistenza elettrica dalla temperatura
Assorbimento di luce ed energia
1. Assorbimento di luce ed effetto serra
2. Le variabili nell'assorbimento di luce
3. Colore e assorbimento di luce
4. Filtri colorati
5. Quanta luce è visibile
Tabella 1 Attività sperimentali su emissione e assorbimento di luce.
Interferenza e diffrazione
La diffrazione è un fenomeno che si incontra ovunque nella vita
quotidiana ed ha innumerevoli applicazioni. Pone un confine inferiore
all’osservazione nel mondo microscopico e nel molto “lontano”:
definisce, infatti, un limite alla capacità di distinzione (risoluzione
ottica) fra due oggetti vicini o relativamente vicini fra loro, perché si
trovano a grande distanza; pone è un limite inferiore all’osservazione
microscopica e all’integrazione (litografia). Realizza un doppio ponte tra
l’ottica geometrica e quella fisica ed tra la fisica classica e quella
quantistica. Costituisce il più semplice caso reale di interferenza e
permette di comprendere nella sua potenzialità i principio di HuygensFresnel. Offre significativa occasione di raccordo tra ipotesi
interpretative (modellizzazione e simulazione) ed esperimento.
Interpretata con un’ipotesi ondulatoria sulla natura della luce, si presta
ad evidenziare la validità del principio di complementarietà, che
12
attribuisce la doppia natura corpuscolare ed ondulatoria alla luce. Si
assiste alla costruzione della figura di diffrazione a singolo fotone
mediante una sorgente a bassissima intensità, che può considerarsi
emettere un fotone alla volta, che attraversa una fenditura di pochi
decimi di millimetro e giunge sullo schermo dietro alla fenditura in
posizione casuale, ma statisticamente determinata dalla distribuzione di
intensità luminosa che determina la figura di diffrazione.
Le proposte su interferenza e diffrazione consentono diverse
modalità di lettura all’interno dell’impostazione delineata.
Quella più generale offre esempi di diffrazione nel quotidiano e
in alcune importanti applicazioni scientifiche e tecnologiche, come
motivazione all’indagine del fenomeno. Essa include tutte le diverse
attività sperimentali illustrate nella Tabella 2.
A. Interferenza da lamina sottile
1. Introduzione (Obiettivi e apparato sperimentale)
2. Prima esplorazione
3. Intensità luminosa riflessa e trasmessa da un cuneo d'aria
4. Riflettanza e trasmittanza di sostanze diverse
5. Angolo di inclinazione locale delle lastre di vetro del cuneo
6. Indice di rifrazione dell'alcool per la luce rossa
7. Influenza della lunghezza d'onda su riflettanza e trasmittanza
8. Indice di rifrazione dell'acqua per radiazione infrarossa
B. Esperimento di Young
Realizzazione e analisi dell'esperimento con luce monocromatica di
diverso colore e della sua interpretazione nelle condizioni di Fraunhofer.
C. Diffrazione
1. Esempi della diffrazione nel quotidiano e in alcune importanti applicazioni
scientifiche e tecnologiche
2. Diffrazione in luce monocromatica e bianca
3. Diffrazione di onde meccaniche
4. Conseguenze della diffrazione: limite al potere risolutivo degli strumenti ottici
5. Conseguenze della diffrazione: sovrapposizione di colori
6. Diffrazione da foro circolare
7. Diffrazione da singola fenditura - Scelte di analisi di distribuzioni sperimentali di
intensità luminosa:
natura angolare della distribuzione
esame qualitativo delle distribuzioni di intensità luminosa da una fenditura in
funzione della posizione acquisite on-line a diversa distanza
leggi empiriche per descrivere la posizione di minimi e massimi; intensità dei
masimi in funzione della loro posizione che del numero d’ordine
l’interpretazione del fenomeno per un fitting dei dati
Tabella2 Attività sperimentali proposte su interferenza e diffrazione.
13
Si aggancia alle proposte di analisi della fenomenologia della
propagazione luminosa per considerare i processi legati a discontinuità
degli assorbitori: la fenomenologia del passaggio della luce attraverso
una finestra, un'apertura ed un piccolo foro. Si trovano così coesistere
con i noti fenomeni di riflessione, rifrazione, assorbimento, anche
fenomeni di diffrazione, che pongono il problema interpretativo della
natura della luce, ovvero del formalismo capace di prevederli. In
particolare una rivisitazione dell'esperienza di Young apre la strada allo
studio dell'interferenza. La caratterizzazione della luce in termini di
onda, o comunque di un ente che nel tempo e nei punti dello spazio si
caratterizza con una ampiezza e una fase, avviene attraverso l'analisi
quantitativa di esperimenti di interferenza da lamina sottile (Corni et al.
1995) e di figure di diffrazione prodotte da aperture sottili o da piccoli
ostacoli (Mascellani et al. 1992). Questa esplorazione prevede sia
esperimenti con sensori di intensità luminosa collegati in linea con il
computer, sia attività di modellizzazione e porta alla costruzione formale
di un modello interpretativo della diffrazione, basato sugli elementi
essenziali dell'ipotesi di Huygens - Fresnel di sorgenti secondarie
puntiformi.
Il confronto, della distribuzione di intensità luminosa prodotta da
due fenditure, con quelle prodotte da ciascuna fenditura, porta al
riconoscimento che la prima non è data dalla somma delle distribuzioni
prodotte dalle singole fenditure. Il modello consente di riconoscere che
la figura (distribuzione di intensità luminosa) prodotta da due fenditure
consiste in una distribuzione di interferenza modulata da una di
diffrazione.
I materiali offerti agli insegnanti nell’ambiente web di SeCiF1
sono articolate su due piani sempre presenti: a) la fisica del fenomeno;
b) la proposta didattica (impostazione e articolazione). Si discutono qui
soltanto i più importanti esiti sperimentali delle attività elencate nella
Tabella 2, per ricostruire il quadro di sintesi dei concetti di base delle
proposte di attività in classe.
14
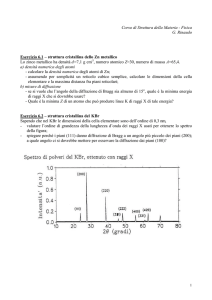
Fig. 5 Grafico sperimentale della distribuzione di intensità luminosa in
funzione della posizione di un sensore di luce in direzione trasversale
rispetto a quello della luce incidente sulla fenditura.
Gli esperimenti consistono nell’acquisizione dell’intensità
luminosa in funzione della posizione con sensori collegati
all’elaboratore per l’individuazione delle leggi fenomenologiche che
caratterizzano la distribuzione di intensità luminosa (fig.5).
Costituiscono attività preliminari esplorazioni qualitative in cui si
visualizza con sensori la distribuzione di intensità luminosa nei
fenomeni di diffrazione prodotti interponendo tra una sorgente
monocromatica e uno schermo: un filo, un capello, un bordo, fenditure
di diversa larghezza.
Nel caso di fenditure sottili (~0.1 mm), viene proposta un’analisi
dettagliata delle caratteristiche delle figure di diffrazione. Si riconosce
che al variare della distanza schermo fenditura, lo schermo intercetta una
distribuzione angolare costante. Dall’analisi delle posizioni xm dei
minimi di intensità, rispetto a quella xo del massimo centrale si riconosce
la correlazione lineare tra (xm - xo) e il numero d’ordine m (fig. 6). Se si
ripete l’analisi con fenditure di diversa ampiezza si ottengono sempre
delle rette, ma di diversa pendenza.
15
Fig. 6 Posizione dei minimi di intensità (xm-xo/D(10-3) ) rispetto al numero
d’ordine m. Si evidenzia una correlazione lineare.
Dall’analisi della posizione X M dei massimi rispetto a xo, si
riconoscere che esiste una relazione lineare anche tra (XM - xo) e il
numero d’ordine M (fig. 7).
Fig. 7 Posizione dei massimi di intensità luminosa (XM-xo/D(10-3) )
in funzione del numero d’ordine M.
16
Dall’analisi degli stessi dati si trova che tra le intensità dei
I
1
massimi e la loro posizione la relazione: M k
(fig. 8).
I0
X M x 0 2
Fig. 8 Intensità dei massimi di intensità luminosa I/Io in
funzione dell’inverso del quadrato della loro distanza dal massimo
centrale (XM-x0)-2.
Dall’analisi delle dimensioni a metà altezza del picco centrale a
parità di distanza da fenditure di diversa larghezza, si riconosce che esso
è tanto più stretto, quanto più larga è la fenditura.
Le attività interpretative sono sviluppate da principi primi,
calcolando gli esiti interferenziali di n sorgenti puntiformi alla fenditura
sul segmento di acquisizione dell’intensità lumiosa (x in fig. 6) con un
software di modellizzazione (Mascellani et al. 1992). Una proposta
alternativa fa riferimento al formalismo dei fasori, che richiede solo
conoscenze di base di algebra vettoriale (Corni et al., 2002).
Diverse sono state le sperimentazioni didattiche in classe di
questa proposta, che ha ispitato anche il progetto SeT “Facciamoluce”4 e
il progetto IRDIS3. Una versione opportunamente semplificata, ma
17
comprensiva dell’esplorazione qualitativa e quantitativa di distribuzioni
di intensità luminosa e dell’attività di modellizzazione per gli aspetti
interpretativi, é stata sperimentata in classe anche da specializzandi5.
Polarizzazione
L’esame della polarizzazione può avviarsi dal percorso sulla
diffrazione, a partire dal riconoscimento che la polarizzazione é una
proprietà della luce discriminante rispetto all'esistenza di figure di
diffrazione.
Una esplorazione iniziale di situazioni quotidiane e applicazioni
tecnologiche della polarizzazione stimola la curiosità degli studenti e li
motiva alla ricerca di interpretazioni. Parimenti motiva lo studio dei
metodi per produrre ed analizzare luce polarizzata. Questo approccio
viene offerto a due livelli: uno elementare, di caratterizzazione
fenomenologica, attraverso leggi empiriche ed uno più formalizzato, che
si basa sull’interpretazione classica della luce come onda
elettromagnetica.
Nella parte introduttiva più generale vengono riproposti e riletti i più
comuni fenomeni di interazione della luce con un materiale rifrangente
(un comune mezzo rifrangente, cristalli birifrangenti, filtri dicroici, come
cristalli di tormalina o i più economici filtri polaroid). L’esame
sperimentale della trasmittanza di una lamina rifrangente fornisce gli
elementi per discutere le modalità con cui la luce interagisce con la
materia, non solo quando viene da essa assorbita, ma anche quando
viene trasmessa o riflessa.
Ad una prima indagine fenomenologica per mezzo di polaroid si
passa alla descrizione quantitativa della polarizzazione lineare con lo
studio sperimentale della legge di Malus.
Fig. 9 Apparato sperimentale per la misura della legge
di Malus con polaroid
18
Con il semplice dispositivo illustrato nella figura 9 si effettua
un’esplorazione qualitativa e poi quantitativa della intensità trasmessa da
un polaroid in funzione dell'angolo relativo, ritrovando la relazione di
Malus (fig10). Si esaminano quindi i principali metodi per produrre luce
polarizzata (riflessione, rifrazione, diffusione, birifrangenza).
Fig. 10 Grafici dell’intensità luminosa misurata dal sensore per luce
incidente non polarizzata (▲) e luce laser (), in funzione dell’angolo
formato dai due polaroid (A) e di cos2 (B).
19
Si evidenzia il carattere unitario dei fenomeni di polarizzazione e
si riconosce la polarizzazione come proprietà trasversale della luce.
L'analisi quantitativa porta al riconoscimento di leggi fenomenologiche,
come quella di Brewster per la luce polarizzata per riflessione e della
trasmittività di polaroid (fig.11) e cristalli birifrangenti.
Fig. 11 Misura della trasmittività di un polaroid
Le attività proposte sono riepilogate nella tabella 3.
La descrizione formale dello stato di polarizzazione avviene
all'interno di questo quadro fenomenologico. attraverso un vettore a cui
è associata una fase La rilettura dei fenomeni indagati in termini di
processi di interazione di singoli fotoni con la materia avvia
all'inerpretazione della legge di Malus in termini probabilistici e alla
costruzione del concetto di stato quantico di un fotone (Michelini,
Ragazzon, et al. 2000). Sperimentazioni didattiche a partire da queste
proposte sulla polarizzazione sono state effettuate anche da
specializzandi nell’ambito della SSIS di Udine (6).
20
1. La polarizzazione nei fenomeni quotidiani e nelle applicazioni
tecnologiche (esplorazioni con polaroid e navigazione in rete)
2. Produrre e analizzare luce polarizzata
3. Le leggi fenomenologiche dell'interazione di luce con polaroid:
Legge di Malus; trasmittività dei polaroid
4. I principali modi per produrre luce polarizzata:
Polarizzazione per riflessione e per rifrazione; Polarizzazione per
diffusione e diffusione di luce polarizzata; Polarizzazione per
birifrangenza
5. Rappresentazione vettoriale della polarizzazione
6. Riflessione e rifrazione di luce e polarizzazione: La legge di Brewster
7. Interazione della luce con cristalli birifrangenti (uniassici): analisi di
situazioni con uno, due cristalli.
Tabella 3. Attività proposte per lo studio della polarizzazione della luce
Simulazioni
Per lo studio della polarizzazione e in particolare nella
prospettiva di un suo utilizzo per l’introduzione della meccanica
quantistica, sono stati sviluppate cinque simulazioni su foglio elettronico
e un applet java per l’ambiente web: JQM. Presentiamo qui
quest’ultimo, come esempio di strumento didattico disponibile nelle
risorse. Si tratta di un ambiente di simulazione per esplorare ipotesi, per
fare previsioni su fenomeni correlati con l’interazione di fotoni
polarizzati con polaroid e cristalli birifrangenti.
L’interfaccia grafica di JQM consente di selezionare gli oggetti
(sorgenti, polaroid, cristalli birifrangenti, rivelatori) con cui simulare
situazioni, eventualmente già esplorate in laboratorio oppure oggetto di
dubbi, per un’analisi di casi. La sorgente di fotoni può essere impostata
in modo da produrre un fotone alla volta, oppure un fascio con un
numero a scelta di fotoni, consentendo di riconoscere, che nei due casi si
ottengono in media gli stessi esiti.
Nella figura 12 é presentata la situazione: luce-polarizzatorerivelatore. Un fascio di fotoni viene generato dalla sorgente (nella figura
12.a viene rappresentato lo stato di ciascun fotone con un segmento
orientato secondo la direzione di polarizzazione). I fotoni interagiscono
con il polaroid con direzione permessa diagonale: una parte di essi viene
assorbita; la parte di essi che viene trasmessa, con probabilità data dalla
legge di Malus (Fig. 12.b) viene conteggiata dal rivelatore (fig. 12.c).
21
Fig. 12 Situazione: sorgente - polaroid con asse di trasmissione a 45°
- rivelatore. a) I fotoni vengono emessi dalla sorgente, b)
interagiscono con il polaroid, venendo trasmessi con probabilità data
dalla legge di Malus, c) vengono conteggiati dal rivelatore.
22
Nella figura 13 viene presentata la situazione: luce-cristallo
birifrangente-rivelatore. Il fascio di fotoni generato dalla sorgente
interagisce con il cristallo birifrangente (nella figura 13b viene
rappresento lo stato in cui possono essere rivelati i fotoni e non i singoli
fotoni). I fotoni vengono rivelati in media nella metà dei casi da uno dei
due rivelatori, nell’altra metà dei casi dall’altro rivelatore. Lo stesso
risultato si ottiene facendo incidere sul cristallo un singolo fotone alla
volta.
Conclusioni
I nuovi mezzi di comunicazione stanno modificando il modo con
cui i ragazzi apprendono, creando nuove occasioni per capire. Ciò
richiede un grande cambiamento nella scuola e nel modo di lavorare
degli insegnanti. Ricerche condotte in collaborazione con diverse unità
di ricerca in didattica della fisica delle università italiane ci hanno
permesso di realizzare strumenti e metodi per la formazione in fisica
degli insegnanti sull’innovazione didattica necessaria e sostenuta dalle
tecnologie dell’informazione e della comunicazione. Nel progetto SeCiF
in particolare sono stati studiati materiali didattici per un radicale
cambiamento nei curricoli di alcuni principali temi sui quali sono state
riscontrate difficoltà concettuali dei ragazzi. Nel progetto FFC sono stati
studiati Moduli di Intervento Formativo (MIF) per la formazione iniziale
degli insegnanti su alcuni grandi temi della fisica di base e della
meccanica quantistica.
Nel campo dell’ottica fisica l’Unità di Ricerca di Udine ha
sviluppato studi e materiali didattici, che si prestano ad essere utilizzati
in forma modulare o come percorso integrato sull’ottica fisica nella
didattica secondaria sui temi: interferenza e diffrazione ottica, emissione
ed assorbimento di luce, polarizzazione lineare della luce, natura della
luce ed interpretazione quantistica.
La rilevanza data all’ottica fisica deriva dalla valenza formativa
che ha il riconoscere, caratterizzare e interpretare la fenomenologia
dell’interazione radiazione-materia, nel ruolo di ponte che gioca tra
ottica geometrica ed elettromagnetismo, tra fisica classica e fisica
quantistica e nella rilevanza dell’ottica fisica sia nella vita quotidiana, sia
in applicazioni in vari campi.
23
Fig. 13 Situazione: sorgente - cristallo birifrangente – rivelatori. a) I
fotoni prodotti incidono sul cristallo, b) si propagano in uno stato di
sovrapposizione (le singole barrette indicano lo stato dei fotoni e non
i singoli fotoni), c) vengono rivelati in metà dei casi dal rivelatore
posto più in alto (in corrispondenza del fascio classico straordinario)
e in metà dei casi dal rivelatore posto più in basso (in corrispondenza
del fascio classico ordinario).
24
I materiali sono progettati per promuovere l’innovazione
didattica e l’attività progettuale. Le diverse proposte si sviluppano dal
piano della esplorazione fenomenologica a quello della costruzione di
interpretazioni con modelli formalizzati.
Lo studio dell’emissione di luce e dell'energia ad essa correlata
sono proposte in termini di esplorazione sperimentale ed analisi
dell'emissione di luce da parte di un filamento di lampadina ad
incandescenza. I processi di assorbimento vengono caratterizzati
attraverso il riconoscimento dei fattori che li determinano.
La fenomenologia della propagazione luminosa nel passaggio
della luce attraverso un materiale rifrangente, un'apertura ed un piccolo
foro consente di riconoscere la coesistenza dei noti fenomeni di
riflessione, rifrazione, assorbimento, accanto a fenomeni di diffrazione,
che pongono il problema interpretativo della natura della luce, ovvero
dei sistemi formali capaci di descriverla. La caratterizzazione della luce
in termini di onda, o comunque come un ente che nel tempo e nei punti
dello spazio si caratterizza con una ampiezza e una fase, avviene
attraverso l'analisi quantitativa di esperimenti di interferenza da lamina
sottile e di figure di diffrazione prodotte da aperture sottili o da piccoli
ostacoli. L’uso di sensori di intensità luminosa collegati in linea con il
computer consente di superare l’approccio semiquantitativo
frequentemente seguito a scuola e di studiare le caratteristiche
dell’intensità luminosa delle frange di diffrazione. Attività di
modellizzazione ispirate all’esperimento ideale dei fori di Young,
portano alla costruzione formale di un modello interpretativo della
diffrazione, basato sugli elementi essenziali dell'ipotesi di Huygens Fresnel di sorgenti secondarie puntiformi. Tale modello fornisce poi
anche le basi interpretative della figura di diffrazione prodotte da due o
più fenditure.
La polarizzazione rappresenta uno speciale ponte concettuale per
l’introduzione della meccanica quantistica nella scuola secondaria. Può
essere trattata a differenti livelli di formalizzazione e in differenti
contesti (fenomenologico descrittivo; ondulatorio, quantistico):
costituisce pertanto un importante elemento di sintesi concettuale
(Cobal, Corni, Michelini 2002). Nell’ambito dei progetti SeCiF ed FFC
25
essa ha costituito un tema significativo per la formazione culturale del
cittadino.
Con un’esplorazione fenomenologica ci si accorge che quando la
luce viene viene trasmessa da un polaroid, un cristallo di tormalina, un
cristallo birifrangente tipo spato d’Islanda, quando é riflessa da una
lamina rifrangente o é soggetta a rifrazioni multiple, o diffusa in
direzione normale alla direzione di incidenza acquista una proprietà
trasversale rispetto alla direzione di propagazione, che prende il nome di
polarizzazione. La legge di Malus descrive in modo unitario gli aspetti
peculiari della fenomenologia della luce polarizzata. Differenti processi
si manifestano simultaneamente in tale fenomenologia e si propone di
passare ad una analisi di situazioni ideali per avviare un approccio
interpretativo. Uno strumento di formalizzazione utilizzato a vari livelli
in questa proposta è la rappresentazione della polarizzazione mediante
un vettore P. Esso può essere riletto come il vettore campo elettrico E (o
magnetico B) in un contesto elettromagnetico o come vettore dello stato
quantico di polarizzazione di singoli fotoni in un contesto quantistico
(Cobal et al. 2002a).
Le diverse proposte sull’ottica fisica sono state utilizzate in
attività formative nella scuola di specializzazione di Udine. I progetti e
gli esiti delle sperimentazioni sono documentati nei materiali sviluppati
per il progetti FFC e in web (www.fisica.uniu.it/URDF/ffc).
Note
1
I principali progetti di ricerca coordinati nazionalmente e validati per la rilevanza a
cui l’Unità di Ricerca in Didattica della Fisica dell’Università di Udine ha
partecipato con specifico ruolo sono:
FISISS -Formazione In Servizio per Insegnanti di Scuola Secondaria. Progetto
MURST-1997/1998, a cui hanno aderito le Unità di Ricerca delle sedi di FE, MI,
MO, NA, PA, PV, TO, UD.
IMOFI - Introduzione ai MOdelli in FIsica. Progetto MIUR-1999, realizzato in
collaborazione dai gruppi di ricerca di MI, NA, PA, PV, TO, UD. L’impiego delle
nuove tecnologie per l’attività sperimentale e la modellizzazione in fisica sono stati il
perno di proposte didattiche originali per la formazione insegnanti.
SeCiF – Spiegare e Capire in Fisica. Progetto MIUR-1999/2000, a cui hanno
partecipato le unità di ricerca di NA, MI-Statale, MI-Bicocca, PA, PV, TO, UD e le
sedi aggregate di BO, FE, MO, TS. I materiali didattici per la formazione degli
insegnanti prodotti sono disponibili in rete telematica: per il gruppo nazionale
all’indirizzo http://pctidifi.mi.infn.it/secif/; per l’Unità di Udine all’indirizzo
www.fisica.uniud.it/URDF.
26
FFC – Fisica per la Formazione Culturale. Progetto MIUR-2001/2003, ha
coinvolto oltre ai gruppi di cui sopra, anche quelli di BO, RM la Sapienza. I materiali
di SeCif sono stati riprocessati per realizzare Moduli di Intevento Formativo (MIF)
per la formazione insegnanti. Il materiale sviluppato a Udine è in gran parte
disponibile in rete all’indirizzo www.fisica.uniud.it/URDF/.
2
Tali proposte sono state sviluppate a partire dalla decennale esperienza maturata nel
settore (Mascellani et al. 1998) nell’ambito dei progetti nazionali SeCiF ed FFC di
cui alla nota1.
3
Si vedano anche i materiali sulla diffrazione del progetto IRDIS (Industria e Ricerca
Didattica
perl’Insegnamento
delle
Scienze),
pubblicati
sul
sito:
www.fisica.uniud.it/URDF/irdis. IRDIS progetto MIUR-L. 6/2000 2001-2002,
coordinato dall’ A.I.F. e realizzato in collaborazione con i Dipartimenti di Fisica
dell’Università di Padova, Bologna, Udine, conclusosi nel dicembre 2003.
4
Nell’ambito delle iniziative MIUR su Scienza e Tecnologia (SeT) sono stati promossi
consorzi per lo sviluppo di materiali didattici da proporre in web. Il consorzio di una
ventina di scuole friulane e il CLDF del CIRD dell’Università di Udine, con capofila
il Liceo Scientifico Marinelli di Udine, ha vinto il bando con il progetto
“Facciamoluce”, conclusosi nel dicembre 2002, con la pubblicazione dei materiali
prodotti nel sito dell’Indire.
5
Degno di nota è il percorso su diffrazione ed interferenza sperimentato da A. Visentin
presso il Liceo Scientifico Grigoletti di Pordenone nell’a.s. 2001-02, nell’ambito del
tirocinio della SSIS di Udine.
6
Sono stati progettati e sperimentati circa una decina percorsi sullo polarizzazione
negli anni 2001-02 e 2002-03.
Bibliografia
M.L. Aiello Nicosia, E. Balzano, N. Bergomi, L. Borghi, E. Giordano, V. Capocchiani,
F. Corni, A. De Ambrosis, C. Marioni, P. Mascheretti, E. Mazzega, M. Michelini, O.
Robutti, L. Santi, E. Sassi, R.M. Sperandeo Mineo, L. Viglietta, G. Vegni, P.
Violino, Teaching mechanical oscillations using an integrated curriculum,
International Journal in Research on Science Education, 19, 8, 1997, pp. 981-995.
Versione in italiano: Una sperimentazione di ricerca sull’impiego delle nuove
tecnologie nella didattica della fisica per il tema delle oscillazioni meccaniche, UeS,
IV, 1/R, p.26
L.W. Anderson Ed., International Encyclopedia of Teaching and Teacher Education
(II Edition), Elsevier Science Ltd., Oxford_UK, 1995
R.E. Benenson, Light Polarization Experiments with Diode Laser Pointer, The
Physics Teacher, Vol. 38, 2000, pp.44-46
S. Bosio, M. Michelini, L'emissione di luce della lampadina da bicicletta, La Fisica
nella Scuola, XXIX, 3, 1996, pp. 154-159
S. Bosio, M. Michelini , Studio delle caratteristiche di alcune lampadine ad
incandescenza, La Fisica nella Scuola, XXX, 2 suppl., 1997 pp. 58 – 61
S. Bosio, M. Michelini, L. Santi, From an incandescent lamp to the electrical
properties of tungsten, in Teaching the Science of Condensed Matter and New
27
Materials, M. Michelini, S. Pugliese Jona, D Cobai eds, GIREP - ICPE Book,
Forum, Udine, 1996, pp. 216-220
S. Bosio, M. Michelini, L. Santi, Da una lampadina alle proprietà elettriche del
tungsteno: un tassello sperimentale per la didattica della fisica, La Fisica nella
Scuola XXXII, 4, 1999, pp. 235-241
S. Bosio, A. Di Pierro, G. Meneghin, M. Michelini, P. Parmeggiani, L. Santi,, A
multimedial proposal for informal education in the scientific field: a contribution to
the bridge between everyday life and scientific knowledge, International Conference
on Science Education for the 21st Century - SciEd21 Book, K Papp, Z Varga, I
Csiszar, P Sik eds, Szeged University, Szeged, Hungary, 1999
S.A. Bradley, P.S. Shaffer, R.N. Steinberg, L.C. McDermott An invetigation of
student understanding of single-slit diffraction and double-slit interference,
American Journal of Physics 67 (2) 1999, pp. 146-155
F. Buchberger, B.P. Campos, D. Kallos, J. Stephenson eds., The green paper on
teacher Education in Europe - High quality teacher education for high quality
education and training, Thematic Network on Teacher Education in Europe
(TNTEE), http://tntee.umu.se/, 2000. Presentazione in italiano: in UeS, 1R, 2000,
p.20 e UeS, 2R, 2000, p.90
S. Caravita, O. Hallden, Reframing the problem of conceptual change, Learning and
Instruction, 4, 1995, p.89
S. Chaudhry and P. Morris Optical fibres: have you seen the light?, Phys. Educ. 35 (4)
2000, pp. 226-231
D. Chauvat, O. Emile, M. Brunel and A. Le Floch Huygens' principle and Young's
experiment in the propagation of light beams, American Journal of Physics, Vol. 71,
No. 11, 2003, pp. 1196–1198
M. Cobal, F. Corni, M. Michelini, Thinking on vectors and formal description of the
light polarization for a new educational approach, in Developing Formal Thinking in
Physics, Michelini M, Cobal M eds, Udine 2001, Girep book with selected papers,
Forum, Udine, 2002 a
M. Cobal, F. Corni, M. Michelini, L. Santi, A. Stefanel, A resource environment to
learn optical polarization, in Physics in new fields, Girep International Conference
proceedings, Lund, 2002 b
D. Colin and J. Rodriguez, A simple medical physics experiment based on a laser
pointer, Am. J. Phys. 70, 2002, pp. 1068
F. Corni, V. Mascellani, E. Mazzega, M. Michelini, G. Ottaviani, A simple on-line
system employed in diffraction experiments, in Light and Information, in Light
and Information , L C Pereira, J A Ferreira, H A Lopes Editors, Girep book,
Univ. do Minho, Braga, 1993, pp.381-388
F. Corni, E. Mazzega, M. Michelini, G. Ottaviani, Capire la Time-Resolved
Reflectivity: una tecnica di analisi basata sull’interferenza da lamina sottile, LFNS,
XXVIII, 1, 1995 pp. 31-38
M. Cobal, F. Corni, M. Michelini, L. Santi , A. Stefanel , A resource environment to
learn optical polarization, in Physics in new fields, Girep International Conference
proceedings, Lund, 2002
28
C. Day, M. Pope, P. Denicolo, Insights into teachers’ thinking and practice, Falmer
Press, London, 1990
D. Easton, Transmission through Crossed Polaroid Filters, The Physics Teacher, Vol.
39, 2001, pp. 231-233
M. Eraut, Developing professional knowledge and competence, Falmer Press, London,
1994
A. M. Gonzales, Light stories: a brief history of light, in Light and Information L C
Pereira, J A Ferreira, H A Lopes Editors, Girep book, Univ. do Minho, Braga, 1993
G. C.Ghirardi, R. Grassi, M. Michelini, A Fundamental Concept in Quantum Theory:
The superposition Principle, in Thinking Physics for Teaching, in Bernardini C,
Tarsitani C and Vicentini eds, Plenum Press, New York, 1995, p.329
G. C. Ghirardi, R. Grassi, M. Michelini, Introduzione delle idee della fisica quantistica
e il ruolo del principio di sovrapposizione lineare, LFNS, XXX, 3 Supplemento, Q7,
1997, pp. 46-57
G. Giugliarelli, M. Michelini, G. L. Michelutti, L. Santi, Tecnologie moderne e
progettualità nell'attività sperimentale per favorire i processi di apprendimento, in
Strategie di insegnamento della fisica: il ruolo del problema e il ruolo del laboratorio,
La Fisica nella Scuola, XXVII, 4 Suppl. Spec., 1994, p.113-135
J. Hernández-Andrés, E. M. Valero, J. L. Nieves, J. Romero Fizeau fringes at home,
American Journal of Physics, Vol. 70, No. 7, 2002, pp. 684–688,
P. F. Hinrichsen, Apparatus and demonstration notes, Am. J. Phys. 69 (8) 2001, pp.
917-919
K. Hirata, How can we use microcomputers effectively in teaching and learning
physics?, Communicating Physics, ICPE (IUPAP), 1986, pag.132
T. T. Grove, A low-cost scanning Fabry--Perot cavity for laser experiments, Am. J.
Phys. 71, 2003, p. 184
C. H. Holbrow, E. Galvez, M. E. Parks, Photon Quantum mechanics and beam
splitters, American Journal of Physics, 70 (3), 2002, pp.260-265;
G. Hudoba, The physics of the compact disc, in Teaching the Science of Condensed
Matter and New Materials, M. Michelini, S Pugliese Jona, D. Cobai eds, GIREPICPE Book, Forum, Udine, 1996, p213-216
C. J. Linder, C. L. McIntyre, D. Marshall, M. R. Nvhodu, Physics tutors’ metalearning
development through an extension of Schön’s reflective practice, Int. J of Sci. Educ.,
19, 1997, pp. 821-833
R. Martongelli, M. Michelini, L. Santi, A. Stefanel, Educational Proposals using New
Technologies and Telematic Net for Physics, in Physics Teacher Education Beyond
2000 (Phyteb2000), R.Pinto, S. Surinach Eds., Girep book, Elsevier, Paris, 2001,
pp.615-620
G. Marucci, M. Michelini, L. Santi, The Italian Pilot Project LabTec of the Ministry of
Education, in Physics Teacher Education Beyond 2000 (Phyteb2000), R.Pinto, S.
Surinach Eds., Girep book, Elsevier, Paris, 2001, pp. 607-610
V. Mascellani, E. Mazzega, M. Michelini, Un sistema per esperienza di ottica on-line e
indicazioni per attività didattiche nello studio della diffrazione ottica, LFNS, XXV,
1 – Speciale, 1992, pp 132-147
29
V. Mascellani, E. Mazzega, M. Michelini, L'elaboratore on-line per lo studio di figure
di diffrazione ottica, Ricerche in Didattica della Fisica, Atti del VII Convegno
Nazionale GNDF, Pavia, 1988, pag. 251
M. Michelini, Supporting scientific knowledge by structures and curricula which
integrate research into teaching, in Physics Teacher Education Beyond 2000
(Phyteb2000), R.Pinto, S. Surinach Eds., Girep book - Selected contributions of the
Phyteb2000 International Conference, Elsevier, Paris, 2001, p. 77-81
M. Michelini, G. L. Michelutti, A. Stefanel, L. Santi, Teacher formation strategies on
physical optics: experimenting the proposal on diffraction, in Quality Development
in the Teacher Education and Training, M. Michelini ed., Girep book of selected
papers, Forum, Udine,2004, …
M. Michelini, A. Mossenta, The EPC Project - Explorating Planning, Communicating,
in Physics Teacher Education Beyond 2000 (Phyteb2000), R.Pinto, S. Surinach Eds.,
Girep book, Elsevier, Paris, 2001, pp.457-460
M. Michelini, P. Pascoli, La luce trasporta energia: esperimenti per la scuola media
con l'elaboratore on – lin, in Boltzmann, Stefan e l'energia radiante: momenti
culturali per la didattica, L. Marcolini Ed. Graphis Udine, 1997 a, p.59
M. Michelini, P. Pascoli, Proposte di esperimenti sull'energia associata alla luce, La
Fisica nella Scuola, XXX, 2 suppl., 1997 b, p. 44 – 51
M. Michelini, S. Pugliese Jona, Computers for Learning Physics, Wirescript 1999
(www.wirescript.com)
M. Michelini, R. Ragazzon, L. Santi, A. Stefanel, Proposal for quantum physics in
secondary school, Physics Education, 35 (6), 2000, pp. 406-410
M. Michelini, L. Santi, A bouncing ball to learn mechanics, in Physics Teacher
Education Beyond 2000 (Phyteb2000), R.Pinto, S. Surinach Eds., Girep book,
Elsevier, Paris, 2001, pp. 147-150
M. Michelini, C. Sartori, Esperienze di laboratorio didattico in una struttura di
raccordo scuola-università, UeS, III, 1/R, 1998, p18-29
M. Michelini, A. Stefanel, L. Santi, Un percorso di esperimenti con sensori on-line in
ottica fisica, in Nuovi obiettivi, curricoli e metodologie nella didattica della
matematica e delle scienze, V Dileo, R Fazio, G Leoci eds, ADT, Bari, 2002, p.146
C. Mirò, R. Pintò, Light production. Categorization of written explanations based on
reasoning patterns, in Research in Science Education in Europe: the picture expands,
M Bandiera, et al. eds, Roma, 2001, pp. 179-187
M. J. Moloney, Homemade Interference, The Physics Teacher, Vol. 37, 1999, pp. 504505
J. O’Connell, Optics Experiments Using a Laser Pointer, The Physics Teacher, Vol.
37, 1999, pp. 445-446
P. J. Ouseph, K. Driver. J. Conklin, Polarization of light by reflection and the Brewster
angle, America Journal of Physics, 69 (11), 2001, pp. 1166-1168
L. C. Pereira, J. A. Ferreira, H. A. Lopes eds , Light and Information, Girep book,
Univ. do Minho, Braga, 1993
R. Pinto, L. Viennot, E. Sassi, J. Ogborn, Research results of the European Project
STTIS , in www.blues.uab.es/~idmc42/sttis.html, 2001
30
G. Pospiech, Uncertainty and complementarity: the heart of quantum physics, Phys.
Educ. 35 (6), 2000, pp. 393-399
S. Pugliese Jona , M. Michelini, Develpoment of a Lab-oriented Hypertextual Teacher
Training and Classroom materials: an example from Geiweb, in Physics Teacher
Education Beyond 2000 (Phyteb2000), R.Pinto, S. Surinach Eds., Girep book,
Elsevier, Paris, 2001, pp. 679-680
S. Pugliese Jona, M. Michelini, A. M. Mancini, Physics teachers at secondary schools
in Italy, in The Training Needs of Physics Teachers in Five European Countries: An
Inquiry, H Ferdinande, S Pugliese Jona, H Latal eds., vol. 4, Eupen Consortium,
European Physical Society, 1999, p.63-89
M. Riel, Educational Change in a technology-rich environment, Journal of Res. In
Computering in Education, 26, 1998, pp. 31-39
T. Sander, F. Buchberger, A. E. Greaves, D. Kallos eds., Teacher Education in
Europe: Evaluation and Perspectives, GmbH, Osnabruck, 1996
L. Santi, E. Mazzega, M. Michelini, Understand radiation Interference by means of
computer modelling, GIREP Book Light and Information, L C Pereira, J A Ferreira,
H A Lopes, Univ. do Minho, Braga, 1993, pp. 372-380
M. B. Schneider, I. A. LaPuma, A simple experiment for discussion of quantum
interference and wich-way measurement, Am. J. Phys. 70 (3), 2002, pp.266-271;
R. M. Sperandeo, I.MO.PHY. (introduction to modeling in physics education) a
Netcourse supporting teachers in implementing tools and teaching strategies, in
Physics Teacher Education Beyond 2000 (Phyteb2000), R.Pinto, S. Surinach Eds.,
Girep book - Selected contributions of the Phyteb2000 International Conference,
Elsevier, Paris, 2001, pp. 135-139
A. Stefanel, M. Michelini, R. Ragazzon, L. Santi, Proposal for quantum physics
learning in secondary school, selected papers of the VIII Inter-American Conference
on Physics Education, Teaching Physics for the Future, A-37, SCdF, Havana, Cuba,
2003
K. Swan, M. Miltrani, The changing nature of teaching and learning in computerbased classrooms, Journal of Res. In Computering in Education, 25, 1998, pp. 121127
C. R. Wheeler, P. N. Henriksen, R. D. Ramsier, Visibility of thin-film interference
fringes, American Journal of Physics -- February 2004 -- Volume 72, Issue 2,
2004,pp. 279-281
K. Wosilait, P. R. L. Heron, P. S. Shaffer, C.L. McDermott, Addressing student
difficulties in applying a wave model to the interference and diffraction of light,
Phys. Educ. Res. Am. J. Phys. Suppl. 67 (7) 1999, pp. S5-S15
31