Esercizi Circuiti Resistivi
Esercizio n°1
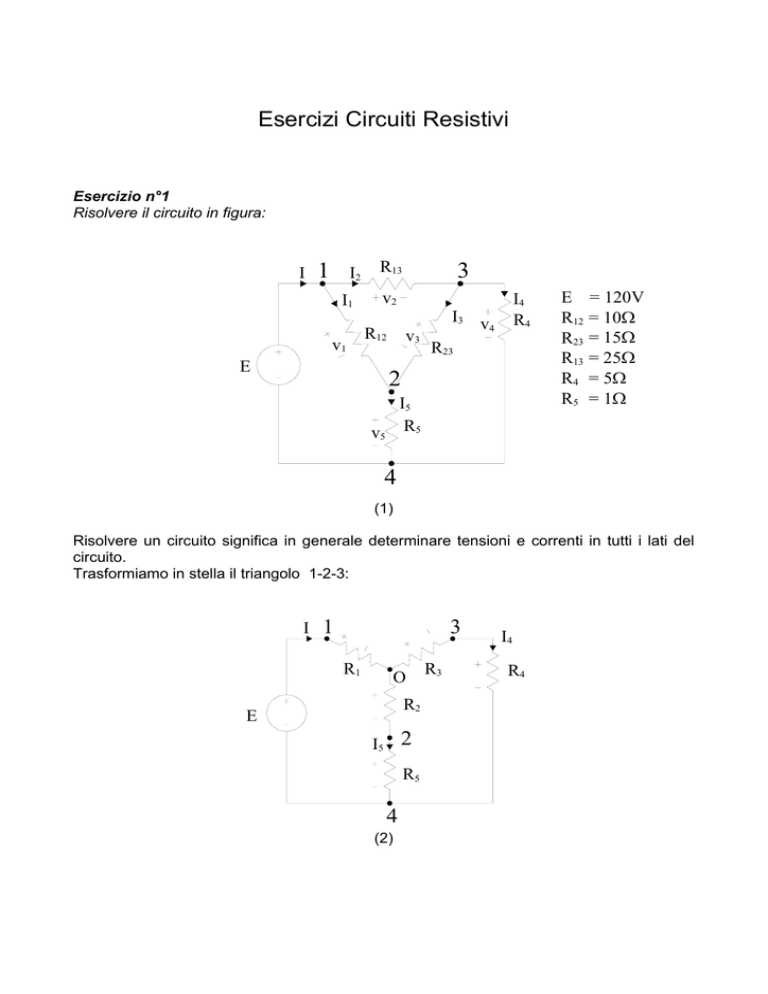
Risolvere il circuito in figura:
I
1
I2
I1
v1
R13
3
v2
R12
E
v3
I4
R4
I3 v
4
R23
2
I5
R5
v5
E = 120V
R12 = 10Ω
R23 = 15Ω
R13 = 25Ω
R4 = 5Ω
R5 = 1Ω
4
(1)
Risolvere un circuito significa in generale determinare tensioni e correnti in tutti i lati del
circuito.
Trasformiamo in stella il triangolo 1-2-3:
I
1
3
R1
O
R2
E
2
I5
R5
4
(2)
R3
I4
R4
dove è:
R1 =
R12 ⋅ R13
10 ⋅ 25
250
=
= 5Ω
=
R12 + R13 + R23 10 + 25 + 15 50
R2 =
R12 ⋅ R23
10 ⋅ 15
150
=
= 3Ω
=
R12 + R13 + R23 10 + 25 + 15 50
R3 =
R13 ⋅ R23
25 ⋅ 15
375
=
= 7.5Ω
=
R12 + R13 + R23 10 + 25 + 15 50
Riduciamo opportunamente il circuito considerando le serie R2, R4 ed R3, R5:
R1
I
O
I5
I4
R25
E
R34
(3)
R25 = R2 + R5 = 3 + 1 = 4Ω
R34 = R3 + R4 = 7.5 + 5 = 12.5Ω
Infine giungiamo ad una configurazione di questo tipo:
I
Req
E
(4)
in cui è:
Req = R1 +
R25 ⋅ R34
4 ⋅ 12.5
50
= 5+
= 5+
= 8.03Ω
4 + 12.5
16.5
R25 + R34
Calcoliamo la corrente I:
I=
E
120V
=
= 14.94 A
Req 8.03Ω
A questo punto, procedendo a ritroso nelle diverse configurazioni ottenute, determiniamo
correnti e tensioni nei diversi lati del circuito.
Determiniamo I5 ed I4 applicando il partitore di tensione e la LKC al nodo O della
configurazione circuitale e (3):
I5 = I ⋅
R34
12.5
= 14.94 ⋅
= 11.32 A
R 25 + R34
12.5 + 4
⇒
I = I5 + I4
I 4 = I − I 5 = 14.94 − 11.32 = 3.62 A
Determiniamo ora le correnti all’interno del triangolo della configurazione di partenza. A
tale scopo impostiamo le L.K.C. ai nodi 1,2,3:
I = I1 + I 2
I1 + I 2 = 14.94
I 5 = I1 + I 3
⇒
I2 = I3 + I4
I1 + I 3 = 11.32
I 2 − I 3 = 3.62
queste relazioni non sono indipendenti tra loro perchè la terza si ottiene sottraendo
membro a membro la prima e la seconda.
E’ necessario quindi cercare una terza relazione; questa ci è fornita dalla L.K.T. applicata
al triangolo della configurazione di partenza:
v2 + v3 − v1 = 0
⇒
R13 I 2 + R23 I 3 − R12 I1 = 0
Il sistema risolutivo diviene quindi:
I1 + I 2 = 14.94
I1 + I 3 = 11.32
R13 I 2 + R23 I 3 − R12 I1 = 0
e conduce ai seguenti risultati:
I 1 = 10.87 A
I 2 = 4.074 A
I 3 = 0.454 A
Note tutte le correnti nei lati del circuito, possiamo determinarne le relative tensioni:
V1 = R12 I1 = 10 ⋅ 10.87 = 108.7V
V2 = R13 I 2 = 25 ⋅ 4.074 = 101.85V
V3 = R23 I 3 = 15 ⋅ 0.454 = 6.81V
V4 = R4 I 4 = 5 ⋅ 3.62 = 18.1V
V5 = R5 I 5 = 1 ⋅11.32 = 11.32V
Esercizio n°2
Dato il circuito in figura:
R1
a
R2
b
E
c
+
v
_
I
i
E
R1
R2
I
= 18V
= 2Ω
= 4Ω
= 2A
d
determinare i e v.
In primo luogo stabiliamo un sistema di riferimento per le tensioni e per le correnti nei lati
in cui questo non è indicato dalla traccia:
a
R1
I1
+
V1
R2
b I2
+
−
E
V2
c
−
+
v
_
I
i
d
Impostiamo la L.K.C. al nodo b:
⇒
I1 = i + I 2
i = I1 − I 2
(1)
Per determinare la corrente I1 applichiamo la L.K.T alla prima maglia:
V1 − E = 0
⇒
V1 = E = R1 I1
⇒
I1 =
E
R1
Per determinare la corrente I2 applichiamo la L.K.C al nodo c:
I + I2 = 0
⇒
I 2 = −I
Sostituendo le espressioni delle correnti I1 e I2 nella (1) otteniamo:
i = I1 − I 2 =
18
E
+ I = + 2 = 11A
2
R1
La tensione v è la tensione ai capi del generatore di corrente che può essere determinata
applicando la L.K.T. alla seconda maglia del circuito:
V2 + v = 0
⇒
v = −V2 = − R2 I 2 = R2 I = 4 ⋅ 2 = 8V
Esercizio n°3
Dato il circuito in figura:
vac
b
a+
R1
− c
R2
+
vbd
_
E1
E2
E1
E2
R1
R2
= 12V
= 8V
= 2Ω
= 4Ω
d
determinare le tensioni vac e vbd.
In primo luogo stabiliamo un sistema di riferimento per le tensioni e per le correnti nei lati
in cui questo non è indicato dalla traccia:
a+
vac
b
V1
I1 + R1 −
E1
+
vbd
_
V2
− c
I2 + R2 −
E2
d
Per ricavare le tensioni vac e vbd è necessario determinare le cadute sui resistori R1 e
R2, per cui il primo passo nella risoluzione di questo circuito consiste nel determinare le
correnti I1 e I2 nei due resistori.
Applicando la L.K.C. al nodo b si ricava evidentemente I 1 = I 2 = I . Impostiamo ora la
L.K.T per l’unica maglia del circuito:
R1 I + R2 I + E 2 − E1 = 0
da cui ricaviamo:
I=
E1 − E 2 12 − 8 2
=
= A
R1 + R2 2 + 4 3
A questo punto possiamo calcolare vac:
vac = R1 I + R2 I = (2 + 4) ⋅
2
= 4V
3
e anche vbd applicando la L.K.T. alla sequenza chiusa di nodi b-c-d:
2
32
vbd = R2 I + E 2 = 4 ⋅ + 8 =
= 10.67 A
3
3
Esercizio n°4
Dato il circuito in figura:
a
R1
b
R
c
i
R2
d
+
v
_
E1
E2
E1
E2
R1
R2
= 12V
= 9V
= 0.1Ω
= 0.3Ω
e
determinare il valore di R per cui è i = 5 A e v = 10V .
V1
In primo luogo stabiliamo un sistema di riferimento per le tensioni e per le correnti nei lati
in cui questo non è indicato dalla traccia:
a
R1
i
b
+ V −
1
R
c
+ V −
R
E1
R2
d
+ + V2 −
v
_
E2
e
Applichiamo la L.K.T. all’unica maglia del circuito:
− E1 + V1 + VR + V2 + E 2 = 0
⇒
− E1 + R1i + Ri + R2 i + E 2 = 0
da cui:
Ri = − R2 i − E 2 + E1 − R1i
R=
− R2 i − E 2 + E1 − R1i − 0.3 ⋅ 5 − 9 + 12 − 0.1 ⋅ 5 1
=
= = 0.2Ω
5
5
i
Calcoliamo ora il valore di R tale che è v = 10V . A tale scopo impostiamo le L.K.T alle
sequenze di nodi c-d-e-c e c-b-a-e-c:
Vcd + Vde + Vec = 0
Vcb + Vba + Vae + Vec = 0
Sostituiamo le tensioni di lato alle tensioni nodo-nodo:
V2 + E 2 − v = 0
− VR − V1 + E1 − v = 0
da cui:
R2 i + E 2 − v = 0
− Ri − R1i + E1 − v = 0
da cui:
i=
v − E2
R2
Ri = − R1i + E1 − v
e quindi:
− R1
R=
v − E2
+ E1 − v − 0.110 − 9 + 12 − 10
R2
0.3
=
= 0.5Ω
v − E2
10 − 9
0.3
R2
Esercizio n°5
Dato il circuito in figura:
R1
a
+
b
V1 −
E
+
V2
R2
−
E
R1
R2
R3
= 36V
= 6Ω
= 2Ω
= 4Ω
− V3 +
d
c
R3
determinare le tensioni V1, V2, V3.
Per ricavare le tensioni ai capi di ciascun resistore possiamo seguire due strade. La prima
consiste nell’applicare il partitore di tensione alla serie R1 - R2 - R3 :
V1 = E
R1
6
216
= 36
=
= 18V
R1 + R2 + R3
6 + 2 + 4 12
V2 = E
V3 = E
R2
2
72
= 36
=
= 6V
R1 + R2 + R3
6 + 2 + 4 12
R3
4
144
= 36
=
= 12V
R1 + R2 + R3
6 + 2 + 4 12
In alternativa possiamo applicare la L.K.T. all’unica maglia del circuito, ricavare il valore
della corrente comune e determinare così le cadute su ciascun resistore. A tale scopo
fissiamo un riferimento per la corrente:
R1
a
+
b
V1 −
E
+
V2
R2
−
− V3 +
d
R3
c
Impostiamo la L.K.T. all’unica maglia del circuito:
V1 + V2 + V3 − E = 0
da cui:
R1 I + R2 I + R3 I − E = 0
I=
E
36
=
= 3A
R1 + R2 + R3 6 + 2 + 4
A questo punto calcoliamo le cadute di tensione ai capi di ciascun resistore:
V1 = R1 I = 6 ⋅ 3 = 18 A
V2 = R2 I = 2 ⋅ 3 = 6 A
V3 = R3 I = 4 ⋅ 3 = 12 A
Esercizio n°6
Dato il circuito in figura:
a
R
R
b
calcolare la resistenza alla porta a-b.
Il cortocircuito si può assimilare ad un resistore di resistenza nulla (e conduttanza infinita).
Il parallelo tra un resistore (in generale di un qualsiasi componente) ed un cortocircuito è
ancora un cortocircuito. Per questo motivo la resistenza alla porta a-b è nulla.
Dato il circuito in figura:
a
R
R
R
b
calcolare la resistenza alla porta a-b.
Il circuito aperto si può assimilare ad un resistore di resistenza infinita (e conduttanza
nulla). La serie tra un resistore (in generale di un qualsiasi componente) ed un circuito
aperto è ancora un circuito aperto. Per questo motivo la resistenza alla porta a-b è pari a
R.
Dato il circuito in figura:
a
R
R
b
calcolare la resistenza alla porta a-b.
La resistenza alla porta a-b è pari a R per le stesse ragioni esposte nell’esercizio
precedente.
Dato il circuito in figura:
a
R
b
R
calcolare la resistenza alla porta a-b.
La resistenza alla porta a-b è nulla perché il parallelo tra un cortocircuito e un resistore (la
serie delle due R ) è ancora un cortocircuito.
Esercizio n°7
Dato il circuito in figura:
R
R
a
b
R
R
calcolare la resistenza equivalente tra a e b.
Il circuito può essere modificato nel seguente modo:
a
2R
2R
b
e infine, effettuando il parallelo tra i resistori di resistenza 2R:
1
1
1
2
1
=
+
=
=
Req 2 R 2 R 2 R R
Req
Req = R
Esercizio n°8
Dato il circuito in figura:
a
R1
R2
R3
R1
R2
R3
R4
R5
R6
R7
R4
b
R5
R6
= 0.25Ω
= 2Ω
= 4Ω
= 3Ω
= 2.5Ω
= 2.5Ω
= 3Ω
R7
calcolare la resistenza equivalente tra a e b.
Riduciamo il circuito partendo dalla serie R2 R3 R7:
a
R1
R4
b
R5
R6
R237 = R2 + R3 + R7 = 2 + 4 + 3 = 9Ω
R237
R1 = 0.25Ω
R4 = 3Ω
R5 = 2.5Ω
R6 = 2.5Ω
R237 = 9Ω
Realizziamo il parallelo R4 R237:
R1
a
R2347
b
R5
1
R2347
=
R1 = 0.25Ω
R5 = 2.5Ω
R6 = 2.5Ω
R2347 = 4/9Ω
R6
1
1 1 1 1+ 3 4
+
= + =
=
9
9
R237 R4 9 3
R2347 = 2.25
A questo punto possiamo determinare la resistenza equivalente effettuando la serie dei
resistori R1 R5 R6 R2347:
Req = R1 + R5 + R6 + R2347 = 0.25 + 2.5 + 2.5 + 2.25 = 7.5Ω
Esercizio n°9
Dato il circuito in figura:
E1
R1
b
a
I1
c
d
R2
I2
R1
R2
E1
E2
I1
I2
E2
e
= 15Ω
= 20Ω
= 30V
= 10V
= 2A
= 4A
ricavare la potenza dissipata nei resistori e la potenza erogata da ciascun generatore.
Fissiamo un riferimento per le correnti e le tensioni nei lati in cui questo non è indicato
dalla traccia:
E1
b IR1
a
c
+ V1 −
IR2 Ig
Vg1
I2
V2
Vg2
−
d
+
+
+
I1
R1
−
−
R2
E2
e
Calcoliamo la potenza dissipata sul resistore R1:
P1 = R1 I R21
A tale scopo impostiamo la L.K.C. al nodo c:
I 2 − I 1 − I R1 = 0
⇒
I R1 = I 2 − I1 = 4 − 2 = 2 A
Si ha quindi:
P1 = R1 I R21 = 15 ⋅ 4 = 60W
Calcoliamo la potenza dissipata sul resistore R2:
P2 = R2 I R2 2 =
V22
R2
R1
R2
E1
E2
I1
I2
= 15Ω
= 20Ω
= 30V
= 10V
= 2A
= 4A
A tale scopo impostiamo la L.K.T. alla maglia contenente i due generatori di tensione:
⇒
E1 − E 2 − V2 = 0
V2 = E1 − E 2 = 30 − 10 = 20V
Si ha quindi:
P2 = R2 I R2 2 =
V22 400
=
= 20W
R2
20
Calcoliamo ora la potenza erogata dai generatori di corrente. A tale scopo calcoliamo Vg1
e Vg2 applicando la L.K.T alla maglia centrale:
V g1 = Vg 2 = V1 + V2 = R1 I R1 + V2 = 15 ⋅ 2 + 20 = 50V
Si ha quindi:
generatore I1:
PI 1 = V g1 I 1 = 50 ⋅ 2 = 100W
generatore I2:
PI 2 = V g 2 I 2 = 50 ⋅ 4 = 200W
Per il generatore I1 abbiamo considerato la convenzione dell’utilizzatore e PI1 > 0 vuol
dire che il generatore sta assorbendo potenza.
Per il generatore I2 abbiamo considerato la convenzione del generatore e PI2 > 0 vuol
dire che il suddetto generatore sta erogando una potenza di 200W.
Calcoliamo ora la potenza erogata dai generatori di tensione. A tale scopo dobbiamo
calcolare la corrente Ig applicando la L.K.C. al nodo c:
I R1 = I R 2 + I g
⇒
I g = I R1 − I R 2 = I R1 −
generatore E1:
PE1 = E1 I g = 30 ⋅1 = 30W
generatore E2:
PE 2 = E 2 I g = 10 ⋅1 = 10W
V2
20
= 2−
= 1A
R2
20
Per il generatore E1 abbiamo considerato la convenzione dell’utilizzatore e PE1 > 0 vuol
dire che il generatore sta assorbendo potenza. Per il generatore E2 abbiamo considerato
la convenzione del generatore e PE2 > 0 vuol dire che il suddetto generatore sta erogando
una potenza di 10W.
Esercizio n°10
Dato il circuito in figura:
R2
a
b
+
V
R3
R1
−
E
R1
R2
R3
E
= 7Ω
= 9Ω
= 6Ω
= 30V
c
ricavare la tensione V.
Fissiamo un riferimento per le correnti e le tensioni nei lati in cui questo non è indicato
dalla traccia:
R2
I2
a
+
I1
+
R1
V2 −
+
R3
V1
E
b
V
−
−
R1
R2
R3
E
= 7Ω
= 9Ω
= 6Ω
= 30V
c
Il dato R1 è in realtà superfluo perché è sufficiente conoscere la tensione ai capi di R1
che è pari a quella del generatore E.
A questo punto per calcolare la tensione V possiamo applicare il partitore di tensione alla
serie R2 – R3:
V =E
R3
6
6
= 30
= 30 = 12V
R2 + R3
6+9
15
Esercizio n°11
Dato il circuito in figura:
a
R1
R3
b
R5
c
R1
R2
R3
R4
R5
R6
E
d
+
E
R2
R4
V
R6
−
I
e
= 2Ω
= 4Ω
= 2Ω
= 4Ω
= 2Ω
= 2Ω
= 50V
ricavare la tensione V e la corrente I.
Fissiamo un riferimento per le correnti e le tensioni nei lati in cui questo non è indicato
dalla traccia:
a I1 + R1 − b I3 + R3 −
c I5 +
+
E
R2
V
I2
−
R5 −
d
+
R4
−
+
R6
−
I6
I
e
R1
R2
R3
R4
R5
R6
E
= 2Ω
= 4Ω
= 2Ω
= 4Ω
= 2Ω
= 2Ω
= 50V
R1
R2
R3
R4
R56
E
= 2Ω
= 4Ω
= 2Ω
= 4Ω
= 4Ω
= 50V
Per calcolare la tensione V riduciamo il circuito di partenza nel seguente modo:
SERIE R5 R6
a I1 + R1 − b I3 + R3 −
c
+
E
R2
I2
+
R4
V
−
−
I
e
R56 = R5 + R6 = 2 + 2 = 4Ω
+
R56
−
I5
PARALLELO R56 R4
a
I1 + R1 − b I3 + R3 −
c
+
E
R2
+
R456
V
I2 −
−
R1 = 2Ω
R2 = 4Ω
R3 = 2Ω
R456 = 2Ω
E = 50V
e
R456 =
R56 ⋅ R4
4⋅4
=
= 2Ω
R56 + R4 4 + 4
SERIE R456 R3
a I1 + R1 − b
+
E
R2
+
R3456
V
−
I2
−
I3
R1 = 2Ω
R2 = 4Ω
R3456 = 4Ω
E = 50V
e
R3456 = R3 + R456 = 2 + 2 = 4Ω
PARALLELO R3456 R2
a I1 + R1 −
b
+
E
R23456
V
−
e
R23456 =
R3456 ⋅ R2
4⋅4
=
= 2Ω
R3456 + R2 4 + 4
R1 = 2Ω
R23456 = 2Ω
E = 50V
A questo punto calcoliamo V applicando il partitore di tensione alla serie R23456 R1:
V =E
R23456
2
= 50
= 25V
R23456 + R1
2+2
Determiniamo la corrente I1:
I1 =
E
R23456 + R1
=
50
= 12.5 A
2+2
Determiniamo la corrente I3 applicando il partitore di corrente al parallelo R3456 R2:
I 3 = I1
R2
4
= 12.5
= 6.25 A
R3456 + R2
4+4
Determiniamo infine la corrente I applicando il partitore di corrente al parallelo R56 R4:
I = I3
R56
4
= 6.25
= 3.125 A
R56 + R4
4+4
Esercizio n°12
Dato il circuito in figura:
I2
a
c
b
I
d
R3
R2
R1
I1
E
e
determinare la corrente I.
Fissiamo un riferimento per le correnti e le tensioni nei lati in cui questo non è indicato
dalla traccia:
I2
a
I1
b IR2
IR1 + + R2 −
R1
c
I
+ R −
3
d
−
E
R1
R2
R3
E
I1
I2
= 10Ω
= 6Ω
= 24Ω
= 10V
= 2A
= 2A
e
Il circuito si risolve impostando le L.K.C. ai nodi b e c e la L.K.T alla maglia contenente i
resistori e il generatore di tensione:
I R1 + I R 2 = I1 + I 2
I R2 = I + I 2
R1 I R1 = R2 I R 2 + R3 I + E
Otteniamo così un sistema di tre equazioni nelle tre incognite IR1, IR2, I
Esplicitiamo le prime due equazioni in funzione di IR2:
I R1 = − I R 2 + I1 + I 2
I = I R2 − I 2
R1 (− I R 2 + I 1 + I 2 ) − R2 I R 2 − R3 ( I R 2 − I 2 ) − E = 0
Dalla terza equazione calcoliamo la IR2:
− R1 I R 2 + R1 I 1 + R1 I 2 − R2 I R 2 − R3 I R 2 + R3 I 2 − E = 0
R1 I R 2 + R2 I R 2 + R3 I R 2 = R1 I1 + R1 I 2 + R3 I 2 − E
I R2 =
R1 I1 + R1 I 2 + R3 I 2 − E 10 ⋅ 2 + 10 ⋅ 2 + 24 ⋅ 2 − 10 78
=
=
= 1.95 A
R1 + R2 + R3
10 + 6 + 24
40
Possiamo calcolare la corrente incognita utilizzando la seconda equazione:
I = I R 2 − I 2 = 1.95 − 2 = −0.05 A = −50mA












