Superconduttori
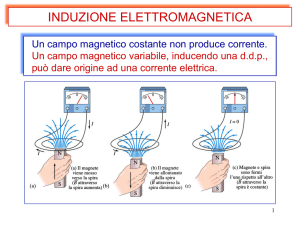
• Molti metalli presentano una
temperatura critica al di sotto
della quale
ρ
– Espellono il campo magnetico
interno (B=0)
– La loro resistivita’ si annulla
• Questa transizione di fase e’ detta
transizione superconduttiva.
• La temperatura critica e’ indicata
Tc e puo’ variare da circa 10K al
di sotto di 0.1 K a seconda del
metallo, della presenza di difetti
nel reticolo cristallino, della
presenza di un campo magnetico
e/o di pressione.
Tc
Β
T
T=cost
Hc
H
Applicazioni della superconduttivita’
• Nei superconduttori possono scorrere
correnti di migliaia di A senza dissipare
alcuna potenza
• Una volta iniettata nel circuito
superconduttore una forte corrente puo’
continuare per centinaia di migliaia di
anni senza bisogno di generatori
esterni.
• I superconduttori vengono quindi usati
per mantenere le correnti necessarie per
generare forti campi magnetici
(magneti superconduttori)
• Queste servono ad es. per ottenere
levitazione magnetica o per fare NMR
o per curvare le traiettorie di particelle
cariche in un collisore di particelle
(CERN LHC) o …
• La superconduttivita’ fu scoperta da H.K.
Onnes nel mercurio nel 1911.
• Solo nel 1957 J. Bardeen, L.N. Cooper e
J.R. Schrieffer riuscirono a formulare una
teoria microscopica della
superconduttivita’, basata sulla
meccanica quantistica (teoria BCS).
• Secondo la BCS il moto di un elettrone di
conduzione distorce leggermente il
reticolo cristallino, facendo avvicinare gli
ioni positivi piu’ vicini al suo passaggio.
• Questa sovradensita’ di ioni positivi
causa l’ attrazione di un altro elettrone,
ed il risultato netto e’ una forza attrattiva
tra elettroni. Il suo effetto e’ la creazione
di coppie di elettroni debolmente legati
(coppie di Cooper, energia 2ε).
• Le coppie si muovono insieme senza
scambiare energia col reticolo.
Applicazioni della superconduttivita’
• Con l’ avvento di materiali
superconduttori ad alta temperatura le
applicazioni si sono moltiplicate.
• Si possono costruire filtri elettronici
senza perdite, quindi con molti piu’
stadi e maggiore efficienza per
selezionare le frequenze desiderate
(quando la resistenza interna di una
induttanza superconduttiva va a zero il
fattore di qualita’ del filtro tende all’
infinito…)
• Si possono costruire motori con
avvolgimenti superconduttori molto
piu’ compatti e piu’ efficienti (motori
da 5000 CV !!)
• Si possono costruire CPU
incredibilmente veloci…
Super
conduttivita’
2ε
≅ 3.. 4
kT c
Coppie di Cooper
• Ogni coppia di Cooper puo’ essere trattata come una
singola particella con massa e carica pari al doppio
di quella di un elettrone.
• La lunghezza di coerenza della funzione d’onda di
un elettrone di conduzione normalmente e’ molto
corta, a cuasa dei continui scattering.
• Ma le coppie di Cooper non sono diffuse, e quindi le
loro funzioni d’onda sono coerenti su distanze molto
grandi (dell’ ordine di 10-4 cm).
• La funzione d’ onda puo’ essere scritta
i ( P⋅r ) / h
Φ P = Φe
1
Coerenza a lungo raggio
• In una densita’ di corrente uniforme tutte le coppie
hanno funzioni d’ onda coerenti e formano un’ unica
funzione d’ onda.
• Questa coerenza a lungo raggio permette di
calcolare fase ed ampiezza della funzione d’ onda in
un punto qualsiasi a partire dal loro valore in un
punto di riferimento. Si puo’ riscrivere come una
onda unidimensionale:
x
ψ P = ψ sin 2π − vt
λ
• La frequenza ν e’ legata all’ energia della coppia di
Cooper, mentre la lunghezza d’ onda e’ legata all’
impulso: λ = h / P
Differenza di fase
• Allora
λ=
Y
∆ϕ
2πm r r
= ϕX − ϕY =
ℑs ⋅ d l
hn s e ∫X
Y
• Se ns e’ la densita’ di elettroni superconduttori, ns/2
e’ la densita’ di coppie di Cooper, e quindi la
supercorrente e’
ns
ℑs =
Flussoide e quanto di flusso magnetico
∆ϕ
XY
∫X
r r
A ⋅ dl
• Da questa formula si puo’ calcolare la
quantizzazione del flusso magnetico in un
anello superconduttore.
• Se nel superconduttore S scorre una
supercorrente, nella zona non superconduttiva
interna N si genera un campo magnetico B.
• La variazione di fase lungo un cammino chiuso del tipo XYZX deve
essere un multiplo di 2π in modo da avere una funzione d’ omda
univoca. Quindi
2πm r r 4π e r r
ℑ s ⋅ dl +
A ⋅ dl →
hns e ∫
h ∫
r r
h
m
=
ℑ ⋅ dl + ∫ B ⋅ dS
n
2e 2ns e 2 ∫ s
S
flussoide
n2π =
quanto di flusso
Φo =
−15
h
= 2 .07 × 10 Wb
2e
2
2ev = ns ev
Effetto del campo magnetico
• Dove A e’ il potenziale vettore del campo magnetico. Nel
caso delle coppie di Cooper
P = 2 m v + 2 eA
• e quindi
• che descrive la variazione di fase delle coppie di
Cooper in un superconduttore.
Y
xˆ
⋅ dl
λ
X
= ϕ X − ϕY = 2π ∫
P = m v + qA
• e quindi
Y
2 π m r r 4π e
=
ℑs ⋅ dl +
hn s e ∫X
h
XY
• In presenza di un campo magnetico la fase viene modificata.
Infatti il momento diventa
hn e
h
h
=
= s
P mv mℑ s
∆ϕ XY
Coerenza a lungo raggio
• Dalla funzione d’ onda si puo’ calcolare la
differenza di fase tra due punti di un
superconduttore nel quale circola corrente.
x
• Per un’ onda piana ψ P = ψ sin 2π − vt
λ
• La differenza di fase dal punto X al punto Y e’
∆ϕ
XY
= ∆ϕ i + ∆ϕ B =
=
2π m Y r r
4π e
ℑ s ⋅ dl +
∫
hn s e X
h
Y
∫
r r
A ⋅ dl
X
Tunnelling Josephson
• Una conseguenza importante della quantizzazione del flusso e’ il
tunnelling Josephson.
• Due zone superconduttrici completamente isolate tra loro hanno
funzioni d’onda con fasi scorrelate.
• Ma se le due regioni vengono avvicinate molto, gli elettroni
potranno diffondere per effetto tunnel da una regione all’ altra.
• Le due funzioni d’ onda dovranno quindi accoppiarsi. L’
accoppiamento sara’ tanto piu’ forte quanto piu’ vicini saranno i
due superconduttori.
• Il tunnelling degli elettroni comporta una corrente superconduttiva
predetta per la prima volta da B.D.Josephson nel 1962.
• La giunzione tra i due superconduttori e’ detta Giunzione
Josephson. La corrente che vi scorre e’
i s = ic sin ∆ ϕ
2
SQUID
SQUID
• Se si accende un campo magnetico
perpendicolare all’ anello, si
genera una differenza di fase delle
onde che passano da XYW rispetto
a quelle che passano da WZX.
Inoltre si genera una piccola
corrente che produce una
differenza di fase ai capi di
ciascuno degli weak links.
• Avremo
• Lo SQUID (Superconducting
Quantum interference Device)
e’ un anello superconduttore
interrotto da due giunzioni
(link deboli in X e W) la cui
corrente critica ic e’ molto
inferiore alla corrente critica
dell’ anello.
• Questo produce una
supercorrente molto bassa,
quindi con impulso delle
coppie anch’esso molto basso.
La lunghezza d’ onda e’ quindi
molto lunga, e quindi la
differenza di fase tra due punti
qualsiasi dell’ anello e’
trascurabile.
n2π = 2∆ϕ i + ∆ϕ B = 2∆ϕi + 2π
• Quindi alla fase dovuta a B si
sottrae o somma una fase dovuta
alla corrente (i- o i+):
φ(B )
i − = i c sin ∆ ϕi = i c sin π
φo
SQUID
Magnetometria SQUID
• Finche’ il flusso e’ tra 0 e Φo/2 e’
piu’ favorevole energeticamente
una corrente in senso antiorario,
che quindi sottrae una differenza di
fase a quella dovuta a B, in modo
che il flussoide valga 0.
• Quando il flusso e’ tra Φo/2 e Φo,
e’ piu’ favorevole una corrente in
senso orario, che aggiunge una
differenza di fase a quella del
flusso in modo da ottenere un
flussoide pari ad h/2e.
• Se il flusso aumenta ancora avremo
una corrente negativa fino 3Φo/2 ,
in modo da matenere il flussoide di
h/2e; poi una positiva per arrivare a
2h/2e e cosi’ via.
• Siccome sinδ non puo’ essere
maggiore di 1, otteniamo la corrente
critica di misura:
• La Ic e’ una funzione
periodica del campo B,
con massimi quando il
suo flusso concatenato
con lo SQUID e’ un
multiplo intero del
quanto di flusso h/2e,
e minimi per multipli
seminteri.
φ (B)
φo
•
•
•
Lo SQUID puo’ essere usato come un
sensibilissimo magnetometro. Si fa entrare
da Y una corrente di misura I (che uscira’
da Z dopo essere fluita in parte da X e in
parte da Y).
Finche’ I e’ piccola non succede nulla, ma
quando raggiunge il valore della corrente
critica negli weak links X e W allora si
genera una tensione.
La condizione di supercodnuttivita’ di
tutto l’ anello e’
φ( B)
α+ β + 2π
•
•
•
I c = 2ic cos(π
φ( B )
)
φo
φo
= 2πn
Dove α e β sono le variazioni di fase
dovute alla corrente totale nei weak links.
Quando si applica I, α e β non sono piu’
uguali, ma la loro somma deve rimanere
costante. Quindi φ( B)
α = πn −
−δ
φo
φ(B)
β = π n −
+δ
φo
Dove δ e’ dovuto alla corrente di misura I.
Quindi 1 I + i = i sin(α)
− 12 I + i = ic sin( β)
c
2
I = 2ic cos(π
φ( B)
) cos δ
φo
Uso dello SQUID
• Di solito non si usa la caratteristica
periodica dello SQUID per misurare il
campo, perche’ non essendo univoca e’
difficile determinare univocamente il
flusso.
• Si preferisce usare il cosi’ detto “flux
locked feedback loop” in cui si avvolge una
bobina intorno alla SQUID e si genera un
flusso che annulla esattamente quello da
misurare. Dalla misura della corrente che si
deve applicare per ottenere l’ annullamento
si stima il flusso da misurare.
• In questo modo lo SQUID lavora sempre in
prossimita’ di zero flusso. La sua
sensibilita’ e’ molto inferiore a Φo .
3
•
•
•
•
Invece di misurare un campo magnetico, si
puo’ misurare una corrente.
Basta far scorrere la corrente da misurare in
un coil “di misura” avvolto intorno allo
SQUID.
Il sistema sara’ quindi composto da:
– 1 SQUID
– 1 avvolgimento di misura
superconduttore
– 1 avvolgimento di feedback
superconduttore
– 1 cilindro superconduttore che scherma
il sistema da campi magnetici
indesiderati
– 1 sistema elettronico per realizzare il
flux-locked loop.
Si crea cosi’ un amperometro estremamente
sensibile (fA) e con resistenza interna nulla:
l’ amperometro ideale. Ha comunque una
induttanza diversa da zero, anche se piccola
(nH)
Uso dello
SQUID
SQUID CS-Blue (Supracon)
ISQUID
IMEAS
IFEEDBACK
Nb
•Size of superconductive screen only 24mm x
ø10mm
•Low input inductance of 320 nH
•Effective coupling of integrated on chip
input coil to the SQUID with mutual
inductance of 10 nH
•Feedback coil integrated on chip coupled to
SQUID with mutual inductance of 230 pH
•Very low current noise better than 1.5
pA/Hz1/2
•Integrated on chip heater to expel frozen
flux
Uso dello SQUID
• Lo SQUID e’ il circuito ideale per misurare il
segnale di corrente proveniente da un bolometro
TES alimentato a tensione costante.
4
Time-domain multiplexing
Multiplexing
• Ge and Si thermistors are read out using JFETs at
100K. There is no pratical way to multiplex many
sensors on a single amplifier. The number of wires
entering the cryostat would be huge for a large
format array. Practical limit: the JFET boxes of
Planck and Hershel…
• TES sensors have very low impedance (about 1 Ω)
• They can be readout by a SQUID with no power
dissipation and large noise margin. Time
multiplex and frequency multiplex are being
developed (NIST, Berkeley, Helsinki ..)
From: Chervenak et al. 99
frequency-domain multiplexing
row i bias
row i+1 bias
j
j+1
Ref: Berkeley/NIST design
5