Elementi di Fisica e applicazioni
Carlo Elce
___________________________________________________________________________________
Corrente elettrica: Leggi di Kirchhoff
La somma delle correnti in un nodo deve essere zero. Oppure, la somma delle correnti
che entrano nel nodo deve essere uguale alla somma delle correnti che escono dal nodo.
Questa è conosciuta come legge della corrente di Kirchhoff.
La somma delle differenze di potenziale in un circuito chiuso deve essere uguale a zero.
Oppure, la somma del voltaggio rilasciato deve equivalere alla somma del voltaggio
delle sorgenti. Questa è conosciuta come la Legge del voltaggio di Kirchhoff.
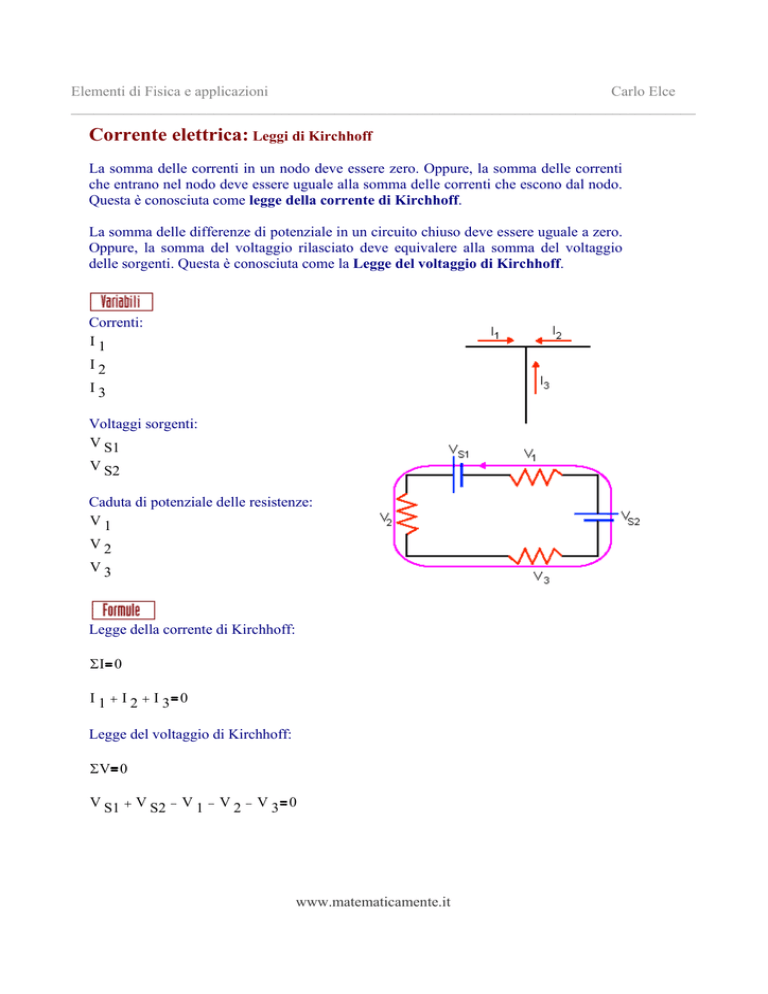
Correnti:
I1
I2
I3
Voltaggi sorgenti:
V S1
V S2
Caduta di potenziale delle resistenze:
V1
V2
V3
Legge della corrente di Kirchhoff:
ΣI 0
I1
I2
I3 0
Legge del voltaggio di Kirchhoff:
ΣV 0
V S1
V S2
V1
V2
V3 0
www.matematicamente.it
Elementi di Fisica e applicazioni
Carlo Elce
___________________________________________________________________________________
Trovare la corrente in ciascuna delle tre diramazioni del seguente sistema:
Da notare che non potete usare le regole per le resistenze in serie e per le resistenze in
parallelo per semplificare il circuito. Così applicate la legge della corrente di Kirchhoff
e la legge del voltaggio di Kirchhoff disegnando le correnti in tre diramazioni e due
circuiti chiusi.
Legge della corrente di Kirchhoff:
I1
I2
I3 0
Legge del voltaggio di Kirchhoff (circuito di sinistra):
6. volt 8. Ω. I 3 0
Legge del voltaggio di Kirchhoff (circuito di destra):
10. volt 2. Ω. I 2
I3
I2
8. Ω. I 3 0
6. volt
8. Ω
10. volt I 3. 8. Ω
2. Ω
www.matematicamente.it
Elementi di Fisica e applicazioni
Carlo Elce
___________________________________________________________________________________
I1
I3
I2
I 1 = 1.25 amp
I 2 = 2 amp
I 3 = 0.75 amp
I
Notate che 1 è negativo. Questo significa che la sua freccia è rivolta nel verso opposto.
Per rendere la corrente positiva, cambiate il verso della freccia.
www.matematicamente.it










