Risposta in frequenza e filtri elementari

Capitolo 6: Risposta in frequenza e filtri elementari
Paragrafo 6.1 Risposta in frequenza sinusoidale
Problema 6.1
Soluzione:
Quantità note:
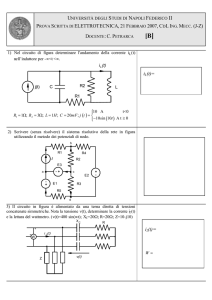
I valori di resistenza ed induttanza, nel circuito di Figura P6.1, R= 200 k
rispettivamente.
ed L= 0,5 H;
Determinare:
a. La risposta in frequenza per il circuito di Fig. P6.1;
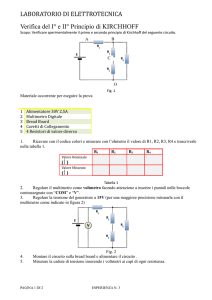
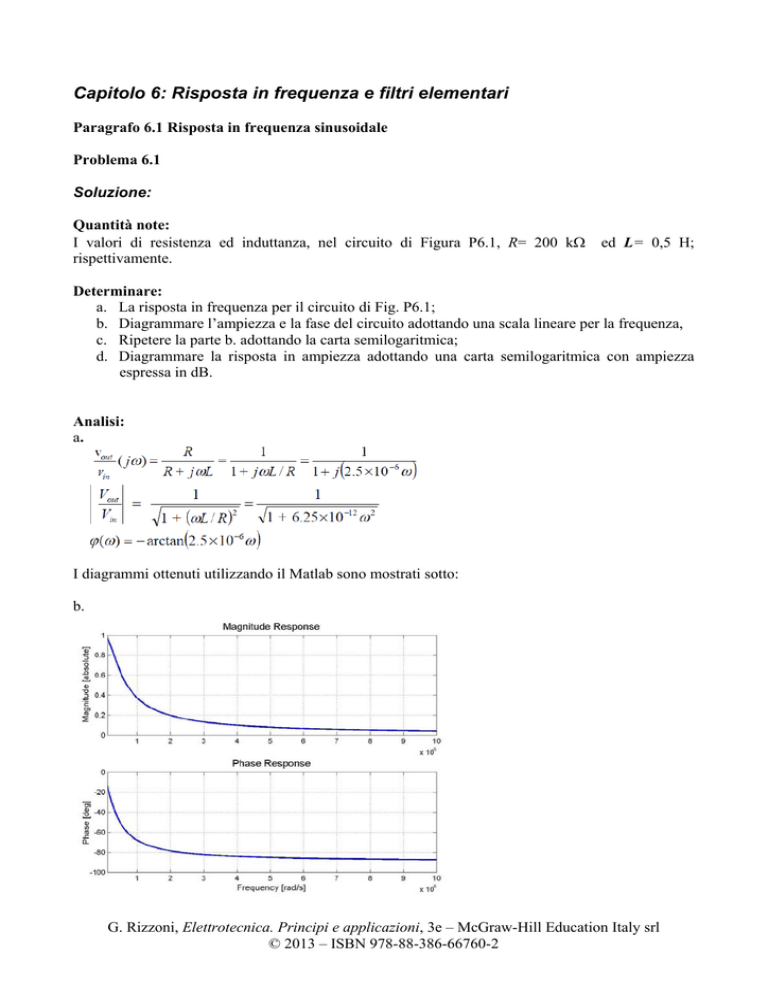
b. Diagrammare l’ampiezza e la fase del circuito adottando una scala lineare per la frequenza,
c. Ripetere la parte b. adottando la carta semilogaritmica;
d. Diagrammare la risposta in ampiezza adottando una carta semilogaritmica con ampiezza
espressa in dB.
Analisi:
a.
I diagrammi ottenuti utilizzando il Matlab sono mostrati sotto:
b.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
c.
d.
Problema 6.2
Soluzione:
Quantità note:
I valori di resistenza e capacità, nel circuito di Figura P6.2.
Determinare:
a. La risposta in frequenza per il circuito di Figura P6.2;
b. Diagrammare l’ampiezza e la fase del circuito adottando una scala lineare per la frequenza,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
c. Ripetere la parte b. adottando la carta semilogaritmica;
d. Diagrammare la risposta in ampiezza adottando una carta semilogaritmica con ampiezza
espressa in dB.
Analisi:
Innanzitutto, troviamo il circuito equivalente di Thevenin visto dal condensatore:
e
a.
b.
I diagrammi ottenuti utilizzando il Matlab sono mostrati sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
c.
d.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.3
Soluzione:
Quantità note:
I valori di resistenza e di capacità, nel circuito di Figura P6.3.
Determinare:
a. La risposta in frequenza per il circuito di Figura P6.3;
b. Diagrammare l’ampiezza e la fase del circuito adottando una scala lineare per la frequenza,
c. Ripetere la parte b. adottando la carta semilogaritmica;
d. Diagrammare la risposta in ampiezza adottando una carta semilogaritmica con ampiezza
espressa in dB.
Analisi:
Innanzitutto, troviamo il circuito equivalente di Thevenin visto dal condensatore:
e
b. I diagrammi ottenuti utilizzando il Matlab sono mostrati sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
c.
d.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.4
Soluzione:
Quantità note:
I valori di resistenza, induttanza e capacità, nel circuito di Figura P6.4.
Determinare:
a. La risposta in frequenza per il circuito di Figura P6.4.
b. Diagrammare l’ampiezza e la fase del circuito adottando una scala lineare per la frequenza.
c. Ripetere la parte b. adottando la carta semilogaritmica;
d. Diagrammare la risposta in ampiezza adottando una carta semilogaritmica con ampiezza
espressa in dB.
Analisi:
a.
b. I diagrammi ottenuti utilizzando il Matlab sono mostrati sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
c.
d.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.5
Soluzione:
Quantità note:
I valori di resistenza, induttanza e capacità, nel circuito di Figura P6.5.
Determinare:
a. La risposta in frequenza per il circuito di Figura P6.5.
b. Diagrammare l’ampiezza e la fase del circuito adottando una scala lineare per la frequenza.
c. Ripetere la parte b. adottando la carta semilogaritmica;
d. Diagrammare la risposta in ampiezza adottando una carta semilogaritmica con ampiezza
espressa in dB.
Ipotesi:
si assuma che la tensione in uscita sia la tensione ai capi del condensatore:
Analisi:
a.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Sostituendo i valori numerici:
b. I diagrammi ottenuti utilizzando il Matlab sono mostrati sotto:
c.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
d.
Problema 6.6
Soluzione:
Quantità note:
I valori di resistenza, induttanza e capacità, nel circuito di Figura P6.6.
Determinare:
a. La risposta in frequenza per il circuito di Figura P6.6.
b. Diagrammare l’ampiezza e la fase del circuito adottando una scala lineare per la frequenza.
c. Ripetere la parte b. adottando la carta semilogaritmica;
d. Diagrammare la risposta in ampiezza adottando una carta semilogaritmica con ampiezza
espressa in dB.
Analisi:
Innanzitutto, troviamo il circuito equivalente di Thevenin visto dal condensatore:
e
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
a.
Quindi,
Sostituendo i valori numerici
b. I diagrammi ottenuti utilizzando il Matlab sono mostrati sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
c.
d.
Problema 6.7
Soluzione:
Quantità note:
Figura P6.7.
Determinare:
a. Come si comporta l’impedenza di ingresso,
basse.
a frequenze estremamente alte o
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
b. Un’espressione per l’impedenza di ingresso.
c. Mostrare che questa espressione può essere manipolata nella forma:
Dove:
d. Determinare la frequenza di taglio alla quale
e. Determinare l’ampiezza e l’angolo di
f. Predire (senza calcolare) l’ampiezza e l’angolo di
.
e
e
Analisi:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.8
Soluzione:
Quantità note:
Figura P6.8.
Determinare:
a. Come si comporta l’impedenza di ingresso
a frequenze estremamente alte
o basse.
b. Un’espressione per l’impedenza di ingresso.
c. Mostrare che questa espressione può essere manipolata nella forma:
Dove:
d. Determinare la frequenza di taglio
e. Determinare l’ampiezza e la fase di
alla quale
f. Predire (senza calcolare) l’ampiezza e la fase di
.
e 10,000
e 10,000 krad/s.
Analisi:
a.
b.
c. In forma standard:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
d.
e. La forma standard può essere ora riscritta come:
Si noti in particolare il comportamento dell’impedenza una decade sotto ed una decade sopra
la frequenza di taglio.
f.
Problema 6.9
Soluzione:
Quantità note:
Con riferimento alla Figura P6.12:
Determinare:
a. Come si comporta l’impedenza di ingresso
o basse.
b. Un’espressione per l’impedenza di ingresso nella forma:
a frequenze estremamente alte
c. Determinare le quattro frequenze di taglio per cui
d. Determinare la frequenza di risonanza del circuito.
e. Diagrammare l’ampiezza dell’impedenza [in dB] come funzione logaritmica della
frequenza, per esempio un diagramma di Bode.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Analisi
c. Sia
che
possono essere positive o negative, e quindi uguali a più o meno uno a
seconda della frequenza; quindi, vanno considerati entrambi i casi.
Dove solo i risultati positivi sono fisicamente validi, ossia, una frequenza negativa è fisicamente
impossibile.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Ancora, le radici negative sono state rigettate poiché fisicamente impossibili.
d. Rappresentando graficamente la risposta in un diagramma di Bode:
Problema 6.10
Soluzione:
Quantità note:
Nel circuito di Figura P6.10.
Determinare:
a. Come si comporta la funzione di trasferimento della tensione
agli
estremi delle alte e basse frequenze.
b. Un’espressione della funzione di trasferimento della tensione, mostrando che può essere
manipolata nella forma:
Dove:
c. La frequenza di taglio per la quale
ed il valore di H0 in [dB]
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Analisi:
Problema 6.11
Soluzione:
Quantità note:
Figura P6.11.
Determinare:
a. Il comportamento della funzione di trasferimento della tensione, o del guadagno, a frequenze
estremamente alte o basse.
b. La tensione di uscita V0 se la tensione di ingresso ha una frequenza dove:
c. La tensione in uscita se la frequenza della tensione in ingresso raddoppia, così che:
d. La tensione in uscita se la frequenza della tensione in ingresso ancora raddoppia, così che:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Analisi:
c.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.12
Soluzione:
Quantità note:
Figura P6.12.
Determinare:
a. La funzione di trasferimento della tensione nella forma
.
b. Tracciare il diagramma di Bode, ossia, un diagramma semilogaritmico dove l’ampiezza [in
dB] della funzione di trasferimento è tracciata su scala lineare in funzione della frequenza su
una scala logaritmica.
Ipotesi:
I valori dei resistori e del condensatore nel circuito di Figura P6.12
Analisi:
a.
b.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.13
Soluzione:
Quantità note:
I valori dei resistori e del condensatore nel circuito di Figura P6.13.
Determinare:
calcolare e tracciare la funzione di risposta in frequenza.
Analisi:
Usando il partitore di tensione:
Tracciando la risposta in un diagramma di Bode:
Sezione 6.2: Analisi di Fourier
Problema 6.14
Soluzione:
Determinare:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Utilizzare le identità trigonometriche per dimostrare che sussistono le uguaglianze nelle equazioni
6.16 e 6.17.
Analisi:
Dall’osservazione della Figura 6.8, possiamo scrivere le seguenti equazioni:
E utilizzare le identità trigonometriche
:
Infine,
Dove,
Problema 6.15
Soluzione:
Quantità note:
L’onda quadra di Figura 6.11(a) nel testo.
Determinare:
Un’espressione generale per i coefficienti della serie di Fourier.
Ipotesi:
Nessuna.
Analisi:
L’onda quadra è una funzione del tempo, come segue:
Possiamo calcolare il coefficiente della serie di Fourier utilizzando gli integrali nelle equazioni
(6.20), (6.21) e (6.22).
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.16
Soluzione:
Quantità note:
La funzione periodica mostrata in Figura P6.16 e definita come:
Determinare:
Un’espressione generale per i coefficienti della serie di Fourier.
Analisi:
Possiamo calcolare i coefficienti della serie di Fourier utilizzando gli integrali nelle equazioni
(6.20), (6.21) e (6.22).
Così, l’espansione in serie di Fourier della funzione è.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.17
Soluzione:
Quantità note:
La funzione periodica mostrata in Figura P6.17 e definita come:
Determinare:
Un’espressione generale per i coefficienti della serie di Fourier.
Analisi:
La funzione in Figura P6.17 è una funzione pari. Perciò, dobbiamo calcolare soltanto i coefficienti
an. Possiamo calcolare i coefficienti della serie di Fourier utilizzando gli integrali nelle equazioni
(6.20) e (6.21).
Problema 6.18
Soluzione:
Quantità note:
La funzione periodica mostrata in Figura P6.18 e definita come:
Determinare:
Calcolare l’espansione in serie di Fourier.
Analisi:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Possiamo calcolare i coefficienti della serie di Fourier utilizzando gli integrali nelle equazioni
(6.20), (6.21) e (6.22).
Così, l’espansione in serie di Fourier della funzione è:
Problema 6.19
Soluzione:
Quantità note:
La funzione periodica mostrata in Figura P6.19 e definita come:
Determinare:
Calcolare l’espansione in serie di Fourier.
Analisi:
La funzione in Figura P6.19 è una funzione pari. Perciò, dobbiamo calcolare soltanto i coefficienti
an. Possiamo calcolare i coefficienti della serie di Fourier utilizzando gli integrali nelle equazioni
(6.20) e (6.21).
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Così, l’espansione in serie di Fourier della funzione è:
Problema 6.20
Soluzione:
Quantità note:
La funzione periodica mostrata in Figura P6.20.
Determinare:
Un’espressione completa per la funzione x(t) ed i coefficienti di Fourier.
Analisi:
La funzione periodica mostrata in Figura P6.20 può essere definita come:
La funzione in Figura P6.19 è una funzione dispari con periodo uguale a 2T. Perciò, dobbiamo
calcolare soltanto i coefficienti bn.
Possiamo calcolare i coefficienti della serie di Fourier utilizzando gli integrali nell’equazione
(6.22):
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.21
Soluzione:
Quantità note:
La funzione periodica mostrata in Figura P6.21.
Determinare:
Un’espressione completa per la funzione x(t) ed i coefficienti di Fourier.
Analisi:
La funzione periodica mostrata in Figura P6.21 può essere definita come:
La funzione in Figura P6.19 è una funzione dispari. Perciò, dobbiamo calcolare soltanto i
coefficienti bn.
Possiamo calcolare i coefficienti della serie di Fourier utilizzando gli integrali nell’equazione
(6.22):
Problema 6.22
Soluzione:
Quantità note:
La funzione periodica definita come:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Determinare:
Tutti i coefficienti della serie di Fourier.
Analisi:
Utilizzando le identità trigonometriche possiamo espandere la funzione x(t) nel modo seguente:
Ora la funzione è già nella forma di una serie di Fourier, poiché essa contiene soltanto termini
sinusoidali. Individuiamo i seguenti parametri:
e tutti gli altri coefficienti sono uguali a zero.
Sezione 6.3: Filtri
Problema 6.23
Soluzione:
Quantità note:
La resistenza del filtro RC passa-alto.
Determinare:
Dimensionare un filtro RC passa-alto con un breakpoint a 200 kHz.
Analisi:
La risposta in frequenza del filtro RC passa-alto è:
La frequenza di taglio è:
Perciò,
Problema 6.24
Soluzione:
Quantità note:
La resistenza del filtro RC passa-basso.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Determinare:
Dimensionare un filtro RC passa-basso in grado di attenuare una tensione sinusoidale a 120 Hz di
20 dB rispetto al guadagno in continua.
Analisi:
La risposta in frequenza del filtro RC passa-basso è:
La risposta del circuito all’ingresso periodico
è:
Al fine di attenuare l’ingresso sinusoidale di 20 dB (un fattore 10) rispetto al guadagno in continua,
Problema 6.25
Soluzione:
Quantità note:
La resistenza e l’induttanza del circuito risonante LC parallelo.
Determinare:
Dimensionare un circuito risonante LC parallelo in modo che la frequenza di risonanza sia 500 kHz.
Analisi:
La risposta in frequenza del circuito risonante LC parallelo è:
La frequenza di risonanza del circuito è:
Il rapporto di smorzamento è:
Il fattore di qualità è:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.26
Soluzione:
Determinare:
In un circuito RLC mostrare che
Analisi:
La risposta in frequenza di un circuito RLC è:
Possiamo calcolare i valori di frequenze 1 e 2 corrispondenti a metà del valore della potenza
nominale (metà-potenza) eguagliando l’ampiezza della risposta in frequenza del filtro passa-basso a
(da ciò si otterrà un’equazione quadratica in , che può essere risolta per le due frequenze).
Definendo
possiamo scrivere la seguente equazione:
Infine, scartando le soluzioni negative:
Perciò:
e
Problema 6.27
Soluzione:
Quantità note:
La resistenza, l’induttanza e la capacità di un circuito risonante RLC serie.
Determinare:
a. Mostrare che l’impedenza alla frequenza di risonanza diventa un valore pari a Q volte la
resistenza induttiva alla frequenza di risonanza;
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
b. Determinare
l’impedenza
assumendo
alla
e
frequenza
di
risonanza,
;
Analisi:
a. L’impedenza di uscita del circuito è:
ed il fattore di qualità è:
Così, per
:
Per un circuito ad alto fattore di qualità abbiamo:
Infine, l’impedenza alla frequenza di risonanza diventa un valore pari a Q volte la resistenza
induttiva alla frequenza di risonanza
b. Il fattore di qualità è:
L’impedenza alla frequenza di risonanza è:
Mentre, Q volte la resistenza induttiva alla frequenza di risonanza è:
Problema 6.28
Soluzione:
Quantità note:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
La risposta in frequenza
del circuito dell’Esempio 6.7.
Determinare:
La frequenza alla quale lo sfasamento introdotto dal circuito è uguale a -10° .
Analisi:
La risposta in frequenza del circuito è:
Dall’esempio 6.7
Lo sfasamento introdotto dal circuito è
Perciò:
Problema 6.29
Soluzione:
Quantità note:
La risposta in frequenza
del circuito dell’Esempio 6.7.
Determinare:
La frequenza in corrispondenza della quale l’uscita del circuito è attenuata del 10 per cento.
Analisi:
La risposta in frequenza del circuito è.
Dall’Esempio 6.7.
L’attenuazione introdotta dal circuito vale:
Perciò
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.30
Soluzione:
Quantità note:
La risposta in frequenza
del circuito dell’Esempio 6.6.
Determinare:
La frequenza in corrispondenza della quale l’uscita del circuito è attenuata del 10 per cento.
Analisi:
La risposta in frequenza del circuito è.
L’attenuazione introdotta dal circuito è:
Perciò
Problema 6.31
Soluzione:
Quantità note:
La risposta in frequenza
del circuito dell’Esempio 6.11.
Determinare:
La frequenza in corrispondenza della quale lo sfasamento introdotto dal circuito è uguale a 20°
Analisi:
La risposta in frequenza del circuito è
Lo sfasamento introdotto dal circuito è:
Così,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.32
Soluzione:
Quantità note:
La
risposta
massima
in
frequenza
del
circuito
di
P6.1,
il
periodo
l’ampiezza
per la forma d’onda a dente di sega.
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi due
termini dell’espansione in serie di Fourier della forma d’onda a dente di sega dell’Esempio 6.3,
abbiamo:
Perciò, per questo problema,
e,
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase.
A questo punto possiamo valutare la risposta in frequenza del sistema alle frequenze 1 e 2
analiticamente:
Infine, possiamo calcolare l’uscita periodica in condizioni stazionarie del sistema
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Il diagramma dei segnali stazionari di ingresso e di uscita è mostrato sotto:
Problema 6.33
Soluzione:
Quantità note:
del circuito di P6.1, il periodo
La risposta in frequenza
per l’onda quadra di Fig. 6.11(a).
l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
L’onda quadra può essere definita come:
Possiamo calcolare i coefficienti della serie di Fourier utilizzando gli integrali nelle equazioni
(6.20), (6.21) e (6.22).
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Utilizzando i primi due termini dell’espansione in serie di Fourier della forma d’onda quadra,
abbiamo:
Perciò, per questo problema,
e,
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 0 e 2
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
Problema 6.34
Soluzione:
Quantità note:
del circuito di P6.1, il periodo
La risposta in frequenza
per la forma d’onda ad impulsi.
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi due
termini dell’espansione in serie di Fourier della forma d’onda ad impulsi dell’Esempio 6.4,
abbiamo:
Così, per questo problema
e,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1 e 2
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.35
Soluzione:
Quantità note:
La risposta in frequenza
del circuito di P6.2, il periodo
e l’ampiezza massima
per la forma d’onda a dente di sega.
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi tre termini
dell’espansione in serie di Fourier della forma d’onda a dente di sega dell’Esempio 6.3, abbiamo:
Così, per questo problema
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1, 2 e 3
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
Problema 6.36
Soluzione:
Quantità note:
La risposta in frequenza
per l’onda quadra.
del circuito di P6.2, il periodo
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi tre termini
dell’espansione in serie di Fourier della forma d’onda quadra di P6.33, abbiamo:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Così, per questo problema
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1 e 3
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.37
Soluzione:
Quantità note:
La risposta in frequenza
del circuito di P6.2, il periodo
per la forma d’onda ad impulsi.
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi due
termini dell’espansione in serie di Fourier della forma d’onda ad impulsi dell’Esempio 6.4,
abbiamo:
Così, per questo problema
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1, 2 e 3
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.38
Soluzione:
Quantità note:
La risposta in frequenza
del circuito di P6.3, il periodo
e l’ampiezza massima
per la forma d’onda a dente di sega.
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi quattro
termini dell’espansione in serie di Fourier della forma d’onda a dente di sega dell’Esempio 6.3,
abbiamo:
Così, per questo problema
e,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1, 2, 3 e
4 analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.39
Soluzione:
Quantità note:
La risposta in frequenza
per l’onda quadra.
del circuito di P6.3, il periodo
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi quattro
termini dell’espansione in serie di Fourier della forma d’onda quadra di P6.33, abbiamo:
Così, per questo problema
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1 e 3
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.40
Soluzione:
Quantità note:
La risposta in frequenza
del circuito di P6.3, il periodo
e l’ampiezza massima
per la forma d’onda ad impulsi.
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi quattro
termini dell’espansione in serie di Fourier della forma d’onda ad impulsi dell’Esempio 6.4,
abbiamo:
Così, per questo problema
e,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1, 2, 3 e
4 analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.41
Soluzione:
Quantità note:
del circuito di P6.4, il periodo
La risposta in frequenza
per la forma d’onda a dente di sega.
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi due
termini dell’espansione in serie di Fourier della forma d’onda a dente di sega dell’Esempio 6.3,
abbiamo:
Così, per questo problema
e,
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1 e 2
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
Problema 6.42
Soluzione:
Quantità note:
del circuito di P6.4, i periodi
La risposta in frequenza
per la forma d’onda a dente di sega.
massima
e
e l’ampiezza
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t). Comparare i diagrammi con quello ottenuto
in P6.41.
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi due
termini dell’espansione in serie di Fourier della forma d’onda a dente di sega dell’Esempio 6.3,
abbiamo:
Così, per questo problema
e,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1,1, 2,1, 1,2
e 2,2 analiticamente:
e,
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
e,
Il diagramma dei segnali stazionari in ingresso ed in uscita per
è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Il diagramma dei segnali stazionari in ingresso ed in uscita per
Confrontando i risultati con
è mostrato sotto:
abbiamo:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.43
Soluzione:
Quantità note:
La risposta in frequenza
per l’onda quadra.
del circuito di P6.4, il periodo
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi due
termini dell’espansione in serie di Fourier della forma d’onda quadra di P6.33, abbiamo:
Così, per questo problema
e,
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alla frequenza 1
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.44
Soluzione:
Quantità note:
La risposta in frequenza
del circuito di P6.4, il periodo
per la forma d’onda ad impulsi.
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi due
termini dell’espansione in serie di Fourier della forma d’onda ad impulsi dell’Esempio 6.4,
abbiamo:
Così, per questo problema
e,
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1 e 2
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.45
Soluzione:
Quantità note:
La risposta in frequenza
del circuito di P6.6, il periodo
e l’ampiezza massima
per la forma d’onda a dente di sega.
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi tre termini
dell’espansione in serie di Fourier della forma d’onda a dente di sega dell’Esempio 6.3, abbiamo:
Così, per questo problema
e,
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1, 2 e 3
analiticamente:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
Problema 6.46
Soluzione:
Quantità note:
La risposta in frequenza del circuito di P6.6, il periodo
la forma d’onda a dente di sega.
e l’ampiezza massima
per
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi tre termini
dell’espansione in serie di Fourier della forma d’onda a dente di sega dell’Esempio 6.3, abbiamo:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Così, per questo problema
e,
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1, 2 e 3
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Confrontando i risultati con
, abbiamo:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.47
Soluzione:
Quantità note:
del circuito di P6.6, il periodo
La risposta in frequenza
per la forma d’onda quadra.
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi tre termini
dell’espansione in serie di Fourier della forma d’onda quadra di P6.33, abbiamo:
Così, per questo problema
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1 e 3
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
Problema 6.48
Soluzione:
Quantità note:
del circuito di P6.6, il periodo
La risposta in frequenza
per la forma d’onda ad impulsi.
e l’ampiezza massima
Determinare:
L’uscita del sistema y(t) come risposta all’ingresso x(t).
Analisi:
In base alle definizioni di serie di Fourier della precedente sezione, ed utilizzando i primi tre termini
dell’espansione in serie di Fourier della forma d’onda ad impulsi dell’Esempio 6.4, abbiamo:
Così, per questo problema
e,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
La risposta in frequenza del sistema può essere espressa nella forma di ampiezza e fase:
A questo punto, possiamo valutare la risposta in frequenza del sistema alle frequenze 1, 2 e 3
analiticamente:
Infine, possiamo calcolare l’uscita periodica del sistema in condizioni stazionarie
Il diagramma dei segnali stazionari in ingresso ed in uscita è mostrato sotto:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.49
Soluzione:
Quantità note:
I valori della resistenza, capacità e induttanza nel circuito di Figura P6.49.
Determinare:
La frequenza di risonanza e l’ampiezza di banda del circuito.
Analisi:
Considerando come uscita la tensione ai capi del sub circuito R-C parallelo,
I diagrammi di Bode corrispondenti sono mostrati sotto:
In questo circuito, all’aumentare della frequenza, l’impedenza del condensatore diminuisce e
l’impedenza dell’induttore aumenta. Entrambi gli effetti causano una diminuzione dell’ampiezza
della tensione in uscita cosicché questo si comporta come un filtro passa-basso del 2° ordine.
La frequenza di risonanza è,
Il rapporto di smorzamento è:
Il fattore di qualità è:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
L’ampiezza di banda è:
Problema 6.50
Soluzione:
Quantità note:
Figura P6.50.
Determinare:
Che tipo di filtri sono quelli mostrati in Figura P6.50.
Analisi:
In [A], all’aumentare della frequenza, l’impedenza del condensatore diminuisce e l’impedenza
dell’induttore aumenta. Entrambi gli effetti causano una riduzione in ampiezza della tensione in
uscita cosicché questo risulta essere un filtro passa-basso del 2° ordine. Si noti che L e C non sono
connessi né in serie né in parallelo e non formano un circuito risonante.
In [B], L e C sono connessi in serie e formano un circuito risonante serie con un’impedenza che è
minima alla frequenza di risonanza e maggiore al di sopra ed al di sotto della frequenza di
risonanza. Questo circuito risonante serie è in serie con l’uscita dando, a causa del partitore di
tensione, una tensione in uscita massima alla frequenza di risonanza ed un valore inferiore per
frequenze più alte e più basse. Perciò [B] è un filtro passa-banda.
In [C], L e C sono connessi in parallelo e formano un circuito risonante parallelo con un’impedenza
che è massima alla frequenza di risonanza e minore al di sopra ed al di sotto della frequenza di
risonanza. Questo circuito risonante parallelo è in parallelo con l’uscita dando, a causa del partitore
di tensione, un’uscita massima alla frequenza di risonanza ed un valore inferiore per frequenze più
alte e più basse. Perciò [C] è un filtro passa-banda.
Problema 6.51
Soluzione:
Quantità note:
Figura P6.51.
Determinare:
Che tipo di filtri sono quelli mostrati in Figura P6.51.
Analisi:
Nessuno degli induttori o condensatori è connesso in serie o in parallelo con altri. Perciò, non vi
sono circuiti risonanti serie o parallelo e nessuno dei circuiti mostrati è un filtro passa-banda o
blocca-banda.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Circuiti [A] e [D]: al tendere della frequenza ad infinito, gli induttori possono essere modellati come
circuiti aperti e i condensatori come cortocircuiti. Perciò, la funzione di trasferimento della tensione
tende a zero. Al tendere a zero della frequenza, gli induttori possono essere modellati come
cortocircuiti ed i condensatori come circuiti aperti. Allora,
Perciò, i circuiti [A] e [D] sono filtri passa-basso.
Circuiti [B] e [C] al tendere della frequenza ad infinito, gli induttori possono essere modellati come
circuiti aperti e i condensatori come cortocircuiti. Allora,
Al tendere a zero della frequenza, gli induttori possono essere modellati come cortocircuiti ed i
condensatori come circuiti aperti. La funzione di trasferimento della tensione tende a zero. Perciò, i
circuiti [B] e [C] sono filtri passa-alto.
Nota: più condensatori ed induttori danno filtri passa-basso e passa-alto di ordine maggiore. Le
migliori performance si ottengono al di fuori della banda passante dove la risposta di questi circuiti
diminuisce di 60 dB/decade. Nei filtri di primo ordine, la risposta si attenua soltanto di 20
dB/decade.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.52
Soluzione:
Quantità note:
Figura P6.52.
Determinare:
a. Se questo è un filtro passa-basso, passa-alto, passa-banda o blocca-banda.
b. Calcolare e diagrammare la funzione di risposta in frequenza se:
Analisi:
a.
Il filtro è un filtro passa-basso.
b. Innanzitutto, determiniamo il circuito equivalente di Thevenin visto dal condensatore:
e,
Perciò,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Sostituendo i valori numerici:
I diagrammi di Bode corrispondenti sono mostrati di seguito:
Problema 6.53
Soluzione:
Quantità note:
I valori dei resistori, della capacità e dell’induttanza del circuito di Figura P6.53.
Determinare:
Calcolare e diagrammare la funzione di risposta in frequenza. I quale tipo di filtro si tratta?
Analisi:
Innanzitutto, determiniamo il circuito equivalente di Thevenin visto dal condensatore.
e, dall’analisi nodale,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Perciò,
Sostituendo i valori numerici:
I diagrammi di Bode corrispondenti sono mostrati di seguito:
L’ampiezza della funzione di trasferimento della tensione ha il massimo in corrispondenza della
frequenza di risonanza e decresce per frequenze maggiori e minori. Quindi, questo è un filtro passabanda.
Comunque, non è un filtro particolarmente buono poiché il guadagno in tensione [o, a dire il vero,
le perdite per inserzione] non è molto diverso alla frequenza di risonanza ed a frequenze più basse.
Ciò è dovuto alle elevate perdite nell’induttore qui modellate come la resistenza equivalente RC. ciò
causa un basso “Q” di circuito.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.54
Soluzione:
Quantità note:
I valori dei resistori, della capacità e dell’induttanza del circuito di Figura P6.53.
Determinare:
Calcolare e diagrammare la funzione di risposta in frequenza. Di quale tipo di filtro si tratta?
Analisi:
Innanzitutto, determiniamo il circuito equivalente di Thevenin visto dal condensatore.
e, dall’analisi nodale,
Perciò,
Sostituendo i valori numerici:
I diagrammi di Bode corrispondenti sono mostrati di seguito:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
L’ampiezza della funzione di trasferimento della tensione ha il massimo in corrispondenza della
frequenza di risonanza e decresce per frequenze maggiori e minori. Quindi, questo è un filtro passabanda.
Nota: la perdita nell’induttore o bobina è più piccola [4]in questo circuito, cosa che consente
migliori performance come filtro passa-banda o un più alto “Q” di circuito. L’ampiezza del rapporto
di trasferimento della tensione o guadagno in tensione [o perdita per inserzione] è più alto alla
frequenza di risonanza che a frequenze più alte o più basse.
Problema 6.55
Soluzione:
Quantità note:
I valori dei resistori, della capacità e dell’induttanza del circuito di Figura P6.55.
Determinare:
a.
b.
c.
d.
Un’espressione della funzione di trasferimento della tensione:
La frequenza di risonanza;
Le frequenze di metà-potenza;
L’ampiezza di banda e Q.
Analisi:
a.
b. La frequenza di risonanza è:
c.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
d. Il rapporto di smorzamento è
Il fattore di qualità è,
L’ampiezza di banda è:
Nota:
1. L’assenza della resistenza di spira ha comportato un guadagno molto più alto alla frequenza
di risonanza che ad alte e basse frequenze.
2. L’ampiezza di banda è piccola se paragonata alla frequenza di risonanza ed il “Q” è
piuttosto grande. Questi dipendono dal carico o dalla dissipazione di potenza della sorgente
e dai resistori di carico e dalla capacità.
3. Un circuito con un alto Q è “selettivo” poiché lascerà passare una banda di frequenze molto
stretta. I circuiti con un “alto” Q hanno un Q=10 o maggiore.
Problema 6.56
Soluzione:
Quantità note:
I valori dei resistori, della capacità e dell’induttanza del circuito di Figura P6.55.
Determinare:
a.
b.
c.
d.
Un’espressione della funzione di trasferimento della tensione:
La frequenza di risonanza;
Le frequenze di metà-potenza;
L’ampiezza di banda e Q.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Analisi:
a.
b. La frequenza di risonanza è,
c.
d. Il rapporto di smorzamento è
Il fattore di qualità è,
L’ampiezza di banda è:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.57
Soluzione:
Quantità note:
I valori dei resistori, della capacità e dell’induttanza del circuito di Figura P6.57.
Determinare:
Calcolare e diagrammare la funzione di risposta in frequenza della tensione. Di quale tipo di filtro si
tratta?
Analisi:
Innanzitutto, determiniamo il circuito equivalente di Thevenin visto dal condensatore.
e,
Perciò,
Sostituendo i valori numerici:
I diagrammi di Bode corrispondenti sono mostrati di seguito:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
L’ampiezza della funzione di trasferimento della tensione ha il minimo in corrispondenza della
frequenza di risonanza e aumenta per frequenze maggiori e minori. Quindi, questo è un filtro
blocca-banda o “notch”.
Alla sua frequenza di risonanza un circuito risonante parallelo ha una resistenza equivalente alta,
cioè è resistivo.
Collegata in serie con il carico, questa alta impedenza riduce l’ampiezza della funzione di
trasferimento della tensione [o guadagno in tensione o perdite per inserzione] alla frequenza di
risonanza.
Il carico dovuto alle perdite dell’induttore, qui modellato come una resistenza equivalente di spira, è
abbastanza piccolo e di conseguenza un guadagno alla frequenza di risonanza sostanzialmente più
basso rispetto al guadagno a frequenze più alte o più basse. Perciò, questo è un circuito con un alto
“Q” con buone performance e selettività. Le perdite nell’induttore influiscono solo lievemente
anche sulla frequenza di risonanza.
E’ difficile [ma non impossibile] determinare le frequenze di taglio nei circuiti che contengono un
circuito risonante parallelo che include le perdite nell’induttore, perciò non è stato fatto alcun
tentativo per calcolarle.
Problema 6.58
Soluzione:
Quantità note:
I valori dei resistori, della capacità e dell’induttanza del circuito di Figura P6.58.
Determinare:
Calcolare e diagrammare la funzione di risposta in frequenza.
Analisi:
Innanzitutto, determiniamo il circuito equivalente di Thevenin visto dal condensatore.
e,
Perciò,
Sostituendo i valori numerici:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
I diagrammi di Bode corrispondenti sono mostrati di seguito:
Problema 6.59
Soluzione:
Quantità note:
Il circuito del filtro mostrato in Figura P6.58.
Determinare:
L’equazione della funzione di trasferimento della tensione in forma standard. Allora, se:
Determinare le frequenze di taglio, l’ampiezza di banda, BW e Q.
Analisi:
Innanzitutto, determiniamo il circuito equivalente di Thevenin visto dal condensatore.
e,
Perciò,
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
I diagrammi di Bode corrispondenti sono mostrati di seguito:
Allora, per calcolare le frequenze di metà-potenza dobbiamo risolvere:
Il rapporto di smorzamento è:
Il fattore di qualità è:
L’ampiezza di banda è:
Problema 6.60
Soluzione:
Quantità note:
Il circuito del filtro mostrato in Figura P6.58.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Determinare:
L’equazione della funzione di trasferimento della tensione in forma standard. Allora, se:
Determinare le frequenze di taglio, l’ampiezza di banda, BW e Q.
Analisi:
Innanzitutto, determiniamo il circuito equivalente di Thevenin visto dal condensatore.
e,
Perciò,
I diagrammi di Bode corrispondenti sono mostrati di seguito:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Allora, per calcolare le frequenze per cui si ha metà della potenza totale, dobbiamo risolvere:
Il rapporto di smorzamento è:
Il fattore di qualità è:
L’ampiezza di banda è:
Problema 6.61
Soluzione:
Quantità note:
Il circuito del filtro blocca-banda mostrato in Figura P6.61, dove:
Determinare:
a. Un’espressione della funzione di trasferimento della tensione o guadagno nella forma:
b. L’ampiezza della funzione ad alte e basse frequenze ed alla frequenza di risonanza;
c. La frequenza di risonanza;
d. Le frequenze di metà-potenza.
Analisi:
a.
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Alla risonanza:
c. Alla frequenza di risonanza la funzione di trasferimento è reale. Ciò richiede che le due
funzioni della frequenza siano uguali:
d. Allora, per calcolare le frequenze di metà-potenza, dobbiamo risolvere:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
Problema 6.62
Soluzione:
Quantità note:
I valori dei resistori, della capacità e dell’induttanza del circuito di Figura P6.55:
Determinare:
a.
b.
c.
d.
Un’espressione per la funzione di trasferimento della tensione:
La frequenza di risonanza;
Le frequenze di metà-potenza.
L’ampiezza della di banda e Q.
e. Diagrammare
Analisi:
a.
b. La frequenza di risonanza è:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2
c. Il rapporto di smorzamento è:
Il fattore di qualità è:
L’ampiezza di banda è:
d. I diagrammi di Bode corrispondenti sono mostrati di seguito:
G. Rizzoni, Elettrotecnica. Principi e applicazioni, 3e – McGraw-Hill Education Italy srl
© 2013 – ISBN 978-88-386-66760-2