Gradiente, divergenza e rotore

Gradiente, divergenza e rotore
Gradiente di una funzione scalare della posizione
Sia f(x,y,z) una funzione scalare continua e derivabile delle coordinate
costruiamo in ogni punto dello spazio un vettore le cui componenti
x,y,z siano uguali alle derivate parziali della funzione f(x,y,z). Questo
vettore prende il nome di gradiente di f (grad f o ∇f)
v
∂f v ∂f v ∂f v
∇f = u x + u y + u z
∂x
∂y
∂z
v ∂ v
∂ v
∂ v
∇ = ux + u y + uz
∂x
∂y
∂z
∇f ci dice come varia la funzione f nell’intorno di un punto, la sua
componente x è la derivata parziale di f rispetto ad x e indica quanto
rapidamente varia f quando ci si muove lungo x.
La direzione di ∇f in un punto qualsiasi è quella in cui, a partire da quel
punto, ci si deve muovere per trovare l’incremento più rapido della
funzione f.
f(x,y,z)
y
∇f
direzione di max pendenza
x
Consideriamo ora la variazione del potenziale V tra (x,y,z) e (x+dx,
y+dy, z+dz)
∂V
∂V
∂V
dV =
dx +
dy +
dz
∂x
∂y
∂z
Sia inoltre ds lo spostamento infinitesimo
v
v
v
v
ds = dxu x + dyu y + dzu z
Ricordando che
Si ottiene
v v
dV = − E • ds
v
v
E = −∇V = − gradV
Il campo elettrico va da zone a V+ a zone a V-, il gradiente di V invece è
un vettore con verso concorde a quello dei V crescenti
v
v
 ∂ v
∂ v 
v
v
V = − kxy ⇒ E = −∇V = − u x + u y (− kxy ) = k ( yu x + xu y )
∂y 
 ∂x
Divergenza di una funzione vettoriale F(x,y,z)
Consideriamo un volume finito V di forma qualsiasi e superficie S, il
flusso della funzione F attraverso S vale
v v
Φ = ∫ F • dS
S
Dividiamo ora il volume V in due parti tramite un diaframma D in
modo da ottenere i due volumi V1 e V2 delimitati da S1 ed S2, con
S1 ed S2 ⊃ D
v v
v v
Φ = ∫ F • dS1 + ∫ F • dS 2
S1
S2
S
1
V1
Suddivido poi il volume in parti sempre più
piccole in modo da avere integrali di superficie
S2 sempre più piccoli.
D
v v N
v v
V2
Φ = ∫ F • dS = ∑ ∫ F • dS i
S
i =1
Si
L’obiettivo è quello di ottenere qualcosa che sia caratteristico di una
regione molto piccola, ovvero una caratteristica locale o puntuale dello
spazio. Ritorna pertanto utile ricorrere alla seguente quantità
v v
∫ F • dS i
Si
Vi
Questo rapporto tende, procedendo per suddivisioni successive, ad un
limite che costituisce una proprietà caratteristica della funzione F in
quell’intorno e che prende il nome di divergenza di F
v
1
divF = lim
Vi →0 V
i
∫
Si
v v
F • dS i
(1)
Naturalmente si dà per scontato che questo limite esista e che esso sia
indipendente da come si fa la suddivisione dello spazio.
Nella pratica la divF è il flusso uscente da Vi per unità di volume nel
caso limite in cui Vi sia infinitesimo.
La divF è una grandezza scalare ed è funzione delle coordinate x,y,z.
v v

F • dS i 
N
v v N
v v
∫
S
 i

F
•
d
S
=
F
•
d
S
=
V
∑
∑
i
i
∫
∫
Si


Vi
i =1
i =1


Per N? ∞ e Vi ? 0, il termine tra parentesi quadre tende alla divF e
ΣVi ? ∫dV, quindi
v v
v
∫ F • dS = ∫ divFdV
S
V
Quest’ultima relazione è il Teorema di Gauss o della divergenza ed è
valido per ogni campo vettoriale per cui la relazione (1) ha un limite.
Nel caso in cui il campo vettoriale F si il campo elettrico E abbiamo
v
v
∫ E • dS = ∫ divEdV
S
V
v v q
ρ
∫SE • dS = ε 0 = ∫V ε 0 dV
v ρ
divE =
ε0
∀ punto
v ∂E x ∂E y ∂E z
divE =
+
+
∂x
∂y
∂z
v
divE > 0 → flusso netto uscente nell' intorno
Laplaciano
Sappiamo che
v
 ∂V v ∂V v ∂V v 
E = − gradV = −
ux +
uy +
u z 
∂y
∂z 
 ∂x
v ∂E x ∂E y ∂E z
divE =
+
+
∂x
∂y
∂z
La componente x di E è Ex= -∂V/∂x, analogamente per le componenti Ey
ed Ez, quindi
v ∂  ∂V  ∂  ∂V
divE =  −
 + −
∂x  ∂x  ∂y  ∂y
 ∂ 2V ∂ 2V ∂ 2V
= − 2 + 2 + 2
∂y
∂z
 ∂x
 ∂  ∂V 
 +  −
=
∂
∂
z
z




 = −div gradV

Definiamo la seguente quantità
∂2
∂2
∂ 2 Laplaciano in coordinate
∇ = 2 + 2 + 2 cartesiane ortonormali
∂x
∂y
∂z
2
Il Laplaciano in coordinate cartesiane può anche essere scritto sotto
forma di prodotto scalare.
v v ∂2
∂2
∂2
∇ = ∇•∇ = 2 + 2 + 2
∂x
∂y
∂z
2
Laplaciano = divergenza del gradiente di...
Allora si ricava
v ρ
ρ
divE = ⇒ ∇ 2V = −
ε0
ε0
Quest’ultima equazione è l’ equazione di Poisson che ha validità locale
e che in modo esplicito si scrive
∂ 2V ∂ 2V ∂ 2V
ρ
+ 2 + 2 =−
2
∂x
∂y
∂z
ε0
Equazione di Laplace
Se ρ = 0 allora il potenziale V deve soddisfare all’equazione di Laplace
∇ 2V = 0
Le soluzioni di questa equazione sono dette funzioni armoniche e godono
della proprietà seguente:
se V(x,y,z) soddisfa l’equazione di Laplace, allora il valor medio di V
sulla superficie di una sfera qualunque (anche non piccola) è uguale al
valore di V calcolato nel centro della sfera.
Un’altra proprietà ci dice che è impossibile realizzare un campo
elettrostatico capace di mantenere una particella carica in equilibrio
stabile nel vuoto.
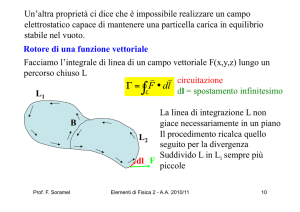
Rotore di una funzione vettoriale
Facciamo l’integrale di linea di un campo vettoriale F(x,y,z) lungo un
percorso chiuso L
v v circuitazione
Γ = F • dl dl = spostamento infinitesimo
L
L1
∫
B
La linea di integrazione L non
giace necessariamente in un piano
L2 Il procedimento ricalca quello
seguito per la divergenza
Suddivido L in Li sempre più
dl F
piccole
v v N
v v
∫ F • dl = ∑ ∫ F • dli
L
i =1
Li
N
Γ = ∑ Γi
i =1
In questo caso torna utile considerare il rapporto tra la circuitazione e
l’area ad essa associata. Tuttavia l’area è un vettore e si deve decidere
come orientarla.
un = versore normale alla superficie Si / un resti costante al tendere a
zero dell’area dell’elemento che circonda un certo punto P, allora
consideriamo il seguente limite
v v
F • dli
∫
Γi
Li
lim oppure lim
Si →0
Si →0 S
Si
i
un
Il verso di un è quello di percorrenza della linea L
(vite destrorsa)
Il limite che otteniamo è uno scalare associato al punto P nel campo
vettoriale F e alla direzione un. La grandezza ottenuta risulta quindi un
vettore
v v
F • dli
v v
∫
Γi
Li
(rotF )• uni = Slim
= lim
0
→
i
Si Si →0
Si
Teorema di Stokes
N
v v N
Γ 
Γ = ∫ F • dl = ∑ Γi = ∑ S i  i 
L
i =1
i =1
 Si 
Per N? ∞ e Si ? 0, il termine tra parentesi tende a (rotF)·uni
v v
v v
 Γi  N


(
)
S
S
rot
F
u
rot
F
=
•
→
• dS
∑
∑
i
i
ni
∫

S
i =1
 Si  i =1
N
quindi
v
v v
v
∫ F • dl = ∫ (rotF )• dS
L
S
Teorema di Stokes
In coordinate caresiane abbiamo
v  ∂Fz ∂Fy  v  ∂Fx ∂Fz  v  ∂Fy ∂Fx  v
u x =
u x + 
rotF = 
−
−
−
u x + 
∂z 
∂x 
∂y 
 ∂z
 ∂x
 ∂y
v
v
v
ux u y uz
∂
∂
∂
=
∂x ∂y ∂z
Fx Fy Fz
infine
v v v
rotF = ∇ × F
Un campo vettoriale con rot ≠ 0 ha circolazione o vorticosità.
Per il campo elettrostatico si ha sempre rotE = 0 condizione sufficiente
perché il campo elettrostatico sia conservativo
Gauss
Grad
Stokes
linea chiusa
superficie
linea
punto
superficie
punto
linea che limita
una superficie
v v
v v
∫ F • dl = ∫ rotF • dS
punti che limitano
una linea
v
V2 − V1 = ∫ gradV • dl
v  ∂Fz ∂Fy  v
v ∂Fx ∂Fy ∂Fz


divF =
+
= rotF =  ∂y − ∂z u x +
+


∂x
∂z
∂y
v v
 ∂Fx ∂Fz  v
= ∇•F
−

u y +
z
∂
x
∂


 ∂Fy ∂Fx  v
v ∂ v
∂ v
∂ v

u z
−
∇ = ux + u y + uz
∂y 
 ∂x
∂z
∂x
∂y
v v
= ∇× F
gradV =
∂V v ∂V v ∂V v
uy +
uz =
ux +
=
∂y
∂z
∂x
v
= ∇V
superficie che limita
un volume
v v
v
∫ F • dS = ∫ divFdV
S
V
L
S
L
Equazioni di Maxwell
Esaminiamo la legge di Ampére
v v
v v
∫ B • dl = µ0i = µ0 ∫ j • d S
L
S
Prendiamo un condensatore e consideriamo il flusso della densità di
corrente attraverso due superfici, entrambe delimitate dalla linea di
integrazione L, ma con S1 che non contiene alcuna armatura ed S2
contenente la prima armatura del condensatore. (carica)
Se consideriamo la superficie S1 delimitata
dalla linea L ed applichiamo Ampére, abbiamo
L S2
che la circuitazione del campo magnetico B
i
S1
risulta proporzionale alla corrente i che scorre
nel circuito ed arriva alla prima armatura del
condensatore. Se invece consideriamo S2,
delimitata da L, abbiamo in entrata la corrente
i, ma non registriamo alcun flusso uscente
Per mantenere tutto consistente dobbiamo ipotizzare, ed è quanto fece
Maxwell, che tra le armature del condensatore vi sia una corrente, non
convenzionale, legata al variare del campo elettrico nel condensatore.
A questa corrente si dà il nome di corrente di spostamento is. Pertanto
la legge di Ampére viene riscritta e prende il nome di legge di Ampére –
Maxwell
v v
ic = corrente
B • dl = µ 0 ic + is
concatenata
L
(
∫
)
Per collegare is al campo elettrico partiamo dal teorema di Gauss
Φ
v
Etot
v v
q
= ∫ E • un dS = int
S
ε0
dΦ Evtot
dq
= ε0
= is
dt
dt
In termini differenziali si ha
v
v
v
∂E
rotB = µ0 j + µ 0ε 0
∂t
mentre in termini integrali abbiamo
v v
d v v
∫LB • dl = µ0ic + µ0ε 0 dt ∫S E • un dS
Riassumendo
v v
qint
E
•
u
dS
=
∫S n
ε0
v v
∫ B • un dS = 0
S
v v
d v v
∫LE • dl = − dt ∫S B • un dS
v v
d v v
∫LB • dl = µ0i + µ0ε 0 dt ∫S E • un dS
v ρ
divE =
ε0
v
divB = 0
v
v
∂B
rotE = −
∂t
v
v
v
∂E
rotB = µ 0 j + µ 0ε 0
∂t