[FORMULARIO] [Per il corso di Data Mining e Statistica per il

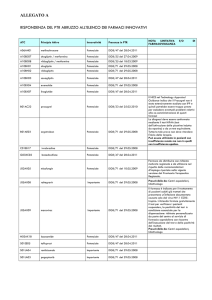
[FORMULARIO]
[Per il corso di Data Mining e Statistica per il Mercato Finanziario]
Antonello D’Ambra
INDICI DESCRITTIVI:
s2 =
r= p
Pn
i=1 (xi
− x̄)2
n
Pn
Pn
(xi − x̄)(yi − ȳ)
i=1 xi yi − nx̄ȳ
p
=
= pPn i=1
Pn
Pn
Pn
2
2 − nx̄2
2
2
2
Dev(x)Dev(y)
(y
−
ȳ)
(x
−
x̄)
x
i=1 yi − nȳ
i=1 i
i=1 i
i=1 i
Cod(x; y)
TEORIA DEL PORTAFOGLIO:
n
r̄t =
vP =
T
X
n
1X
ri
n i=1
sb2t =
1 X
(ri − r̄t )2
n − 1 i=1
vt × at
wt =
vP
vt × at
t=1
r̄P =
T
X
r̄t × wt
t=1
sb2P = (w1 × sb1 )2 + (w2 × sb2 )2 + (2 × w1 × w2 × sb1 × sb2 × r12 )
sb2P = (w1 ×b
s1 )2 +(w2 ×b
s2 )2 +(w3 ×b
s3 )2 +(2×w1 ×w2 ×b
s1 ×b
s2 ×r12 )+(2×w1 ×w3 ×b
s1 ×b
s3 ×r13 )+(2×w2 ×w3 ×b
s2 ×b
s3 ×r23 )
MODELLO DI REGRESSIONE SEMPLICE:
Cod(x; y)
b1 =
=
Dev(x)
Pn
Pn
(xi − x̄)(yi − ȳ)
xi yi − nx̄ȳ
i=1
Pn
= Pi=1
n
2
2
2
(x
−
x̄)
i=1 i
i=1 xi − nx̄
B1 ∼ N β1 ;
σ2
Dev(x)
b0 = ȳ − b1 x̄
1
x̄2
B 0 ∼ N β0 ; σ 2
+
n Dev(x)
sse = Dev(Y ) − b21 Dev(X)
sse = Dev(Y ) − b1 Cod(X; Y )
IL MODELLO DI REGRESSIONE MULTIPLA:
B ∼ N β; σ 2 (XT X)−1
DIAGNOSTICA DEL MODELLO DI REGRESSIONE:
−1 (i − 0.5)
zi = Φ
δ = max[|F (x) − Φ(x)|]
n
Ppos
Pn
[ i=1 ai (xn−i+1 − xi )]2
(e
− e )2
i=2
Pn
Pni−1 2 i
w=
dw
=
2
i=1 (xi − x̄)
i=1 ei
1
MODELLI PER DATI PANEL:
Sorgente
Regressione
Residuo
Totale
Devianza
SSR
SSE
SST
Within/Dummy
n+k−1
N −k−n
N −1
GdL
Between
k
n−k−1
n−1
FGLS
k
N −k−1
N −1
Test di Hausman:
H = (BW − BF GLS )T [VC(BW ) − VC(BF GLS )]−1 (BW − BF GLS ) =
(BW − BF GLS )2
∼ χ2k
[VC(BW ) − VC(BF GLS )]
IL MODELLO DI REGRESSIONE LOGISTICA:
T
−1
B ∼ N β; (X VX)
exp(b0 + b1 xi1 + b2 xi2 + . . . + bk xik )
1 + exp(b0 + b1 xi1 + b2 xi2 + . . . + bk xik )
pi =
n
X
ln[L(y; b)] =
[yi ln(pi ) + (1 − yi ) ln(1 − pi )]
ln[L(y; 0)] = n1 ln
i=1
2
rM
=1−
1−
2
rN
=
L(y;b)
L(y;0)
L(y; b)
L(y; 0)
n2
= 1 − exp
n2
1 − exp
2
1 − [L(y; b)] n
=
−
n1
n
+ n2 ln
n2
n
2
ln[L(y; b)] − ln[L(y; 0)]
n
ln[L(y; b)] − ln[L(y; 0)]
2
rM
=
2 )
max(rM
1 − exp n2 ln[L(y; b)]
−
2
n
MASSIMA VEROSIMIGLIANZA:
Variabile Casuale Bernoulliana
L(x; π) = π
Pn
i=1
xi
(1 − π)
n−
Pn
i=1
xi
ln[L(x; π)] = ln(π)
n
X
n
X
xi + ln(1 − π)
(1 − xi )
i=1
i=1
Pn
S(x; π) =
i=1
xi
π
Pn
−
n − i=1 xi
1−π
=(T M L ) =
n
π(1 − π)
Variabile Casuale Poissoniana
Pn
λ i=1 xi
L(x; λ) = exp(nλ) Qn
i=1 xi !
ln[L(x; λ)] = −nλ + ln(λ)
n
X
i=1
n
S(x; λ) = −n +
1X
xi
λ i=1
=(T M L ) =
xi −
n
X
i=1
n
λ
Test statistici
LR =
L
−2{ln[L(x; tM
vincolata )]
− ln[L(x; t
ML
L
L(x; tM
vincolata )
)]} = −2 ln
L(x; tM L )
2
T M L − θ0
W = p
=(T M L )−1
2
ln(xi !)