Laboratorio R
Corso di Algebra e Modelli lineari
(Anno Accademico 2015-16)
REGRESSIONE LINEARE SEMPLICE
OPEN STATISTICA
8.44
Per 8 settimanali, appartenenti alla medesima fascia di prezzo e presenti in edicola a una certa
data, sono stati rilevati il numero X di pagine dedicate ad arte e cultura e le vendite Y (in milioni di
lire) effettuate nella settimana. I dati sono riportati nella seguente tabella:
X
0
1
2
5
7
10
14
20
Y
375
450
500
725
800
950
1025
1200
a) Si stimino con il metodo dei minimi quadrati i parametri β0 e β1 del modello: Y=β0 + β1X + ε
In R i due vettori dei dati X e Y vengono costruiti come segue:
> x<-c(0,1,2,5,7,10,14,20)
> y<-c(375,450,500,725,800,950,1025,1200)
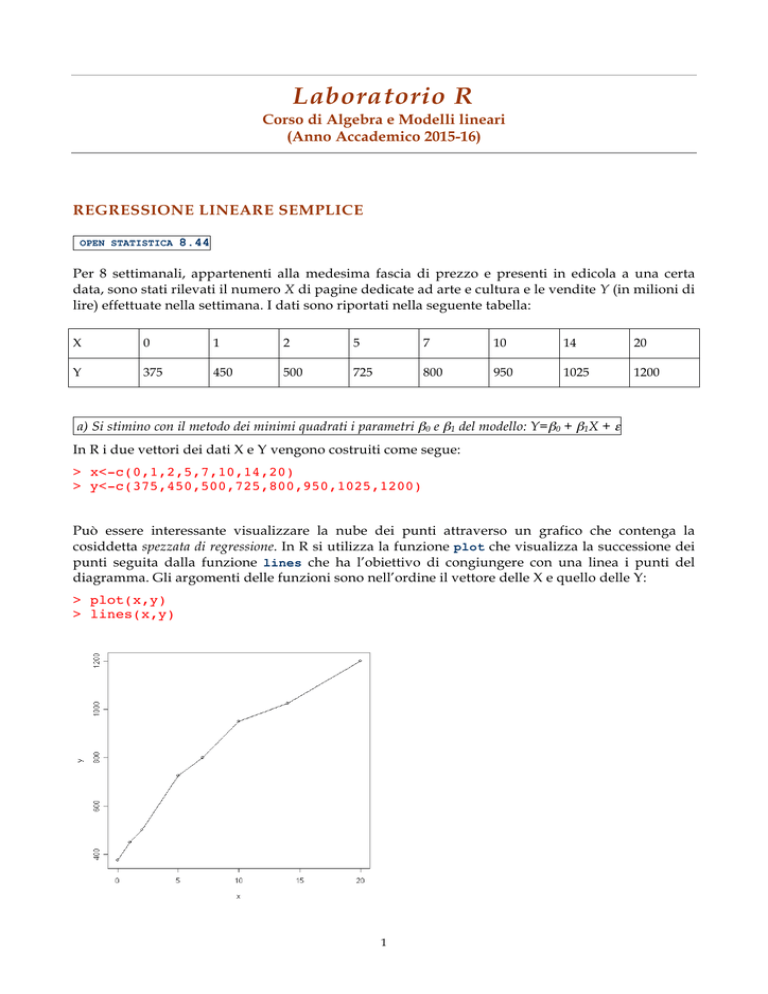
Può essere interessante visualizzare la nube dei punti attraverso un grafico che contenga la
cosiddetta spezzata di regressione. In R si utilizza la funzione plot che visualizza la successione dei
punti seguita dalla funzione lines che ha l’obiettivo di congiungere con una linea i punti del
diagramma. Gli argomenti delle funzioni sono nell’ordine il vettore delle X e quello delle Y:
> plot(x,y)
> lines(x,y)
1
Esistono altri argomenti opzionali per la personalizzazione del grafico (relativamente agli assi, ai
titoli, legenda, colori ecc.). Per una più dettagliata trattazione si rimanda all’help in linea del
linguaggio R:
> help(plot)
Per stimare i parametri della retta di regressione si può procedere calcolando dettagliatamente
tutte le formule derivanti dal metodo dei minimi quadrati oppure utilizzando le funzioni già
predisposte a questo proposito in R. Relativamente al primo approccio, (più laborioso ma
sicuramente più costruttivo!) è necessario valutare medie, devianze e codevianze. Si costruiscano i
vettori scarto dalle medie utilizzando la funzione mean che calcola la media aritmetica di una
successione di valori:
> x.scarti<- x-mean(x)
> y.scarti<- y-mean(y)
La devianza di X, quella di Y e la codevianza risultano allora:
> dev.x <- sum(x.scarti^2)
> dev.y <- sum(y.scarti^2)
> codev.xy <- sum(x.scarti*y.scarti)
L’intercetta e il coefficiente di regressione risultano quindi:
> b1 <- codev.xy/dev.x
[1] 41.45826
> b0 <- mean(y)-mean(x)*b1
[1] 447.3704
Alternativamente per stimare un modello di regressione lineare si può utilizzare la funzione lm.
Tale funzione è può essere utilizzata più in generale per vari tipi di modelli lineari, quali modelli
di regressione lineari e multipli, analisi della varianza e analisi della covarianza. Come ogni altra
funzione, lm prevede argomenti necessari e facoltativi. Quello indispensabile in questo caso è una
formula, ovvero una descrizione simbolica del modello da stimare. La descrizione deve essere fatta
in questo modo:
variabile risposta ~ variabili esplicative
pertanto in questo contesto la funzione sarà:
> output.reg.lin <- lm(y~x)
Il risultato della regressione lineare è racchiuso in una lista un oggetto complesso in R articolato in
più vettori, matrici o altri oggetti. Al fine di visualizzare separatamente gli oggetti della lista si
utilizza il simbolo $ seguito dal nome dell’oggetto stesso. La stima dei parametri è contenuta nel
vettore coefficients:
> output.reg.lin$coefficients
(Intercept)
447.37036
x
41.45826
A questo punto è possibile visualizzare graficamente la retta di regressione. A tal proposito si
valutino i valori teorici:
> y.teorici<-b0+b1*x
2
Se si vuole ottenere un grafico che visualizzi la retta passante attraverso la nube dei punti
osservata si digitino le funzioni plot per la nube dei punti e points che aggiunge una serie di dati
ad un grafico corrente. Con le opzioni type=“l” e col=“2” (rosso) si intende rappresentare una
linea continua e di colore rosso:
> plot(x,y)
> points(x,y.teorici,type="l",col="2")
Si potevano altresì utilizzare i comandi:
> plot(x,y)
> abline(output.reg.lin)
b) Si determinino gli intervalli di confidenza al 99% per il coefficiente angolare e l’intercetta
Prima di utilizzare l’output derivante dalla funzione lm si proceda per passi, calcolando tutte le
quantità necessarie per le formule:
b1 ± tα 2;n − 2
s ydisp
∑ (x
− x)
2
j
j
1
x2
+
n ∑ (x j − x )2
bo ± tα 2;n − 2 s ydisp
j
La radice quadrata della varianza di dispersione si può calcolare nel seguente modo:
> dev.disp<-sum((y-y.teorici)^2)
[1] 30124.13
> s.disp<-sqrt(dev.disp/6)
[1] 70.85681
3
Alternativamente l’output della funzione lm comprende i valori teorici e i residui negli oggetti
denominati rispettivamente fitted.values e residuals. Pertanto la devianza di dispersione si
poteva ottenere anche nel seguente modo:
> dev.disp<-sum((output.reg.lin$residuals)^2)
Il valore teorico della distribuzione t di Student in corrispondenza di un determinato livello di
significatività lo si determina facendo ricorso alla funzione qt. Tale funzione (cosi come le funzioni
qnorm, qbinom, qf, ecc.) determina il valore di ascissa della funzione di ripartizione in modo che
l’area alla sua sinistra corrisponda ad una determinata frazione percentuale. La funzione prende
due argomenti necessari: la frazione percentuale dell’area e i gradi di libertà. Essendo l’intervallo
di confidenza pari al 99% si noti che
> qt(0.005,6)
[1] -3.707428
> qt(0.995,6)
[1] 3.707428
essendo la distribuzione t simmetrica e pertanto il valore teorico di t è dato da:
> t.value<-qt(0.995,6)
Ora gli estremi dell’intervallo di confidenza per il coefficiente angolare sono dati da:
> inf.b1<-b1-t.value*s.disp/sqrt(dev.x)
[1] 27.20892
> sup.b1<-b1+t.value*s.disp/sqrt(dev.x)
[1] 55.7076
mentre quelli per l’intercetta sono dati da:
> sup.b0<-b0+t.value*s.disp*sqrt(1/8+(mean(x)^2/dev.x))
[1] 587.6196
> inf.b0<-b0-t.value*s.disp*sqrt(1/8+(mean(x)^2/dev.x))
[1] 307.1211
c) Il valore della variabile Y, y0, quando xd =7
Si tratta di un problema di previsione: poiché non si è in grado di prevedere in maniera esatta il
valore di una singola estrazione occorre determinare l’intervallo di confidenza per il valore y0. Tale
intervallo viene determinato applicando la formula:
1
(xd − x )2
i = ( b0 + b1 xd ) ± tα 2;n−2 sydisp 1+ +
n ∑( x j − x )2
j
Dunque si avrà:
> inf.y0<-b0+b1*7-(t.value*s.disp*sqrt(1+1/8+((7-mean(x))^2/dev.x)))
[1] 458.8952
> sup.y0<-b0+b1*7+(t.value*s.disp*sqrt(1+1/8+((7-mean(x))^2/dev.x)))
[1] 1016.261
4
OPEN STATISTICA
8.44
Si sono valutati i consumi di 10 utilitarie di case automobilistiche diverse con i seguenti risultati:
Velocità in miglia per 50
ora (X)
55
60
65
70
75
Consumo in miglia 34.8
per gallone (Y)
33.6
34.6
32.8
32.6
31.6
30.9
34.1
31.9
31.8
a) Si stimi il modello di regressione di Y su X
> x<-c(50,50,55,55,60,60,65,70,70,75)
> y<-c(34.8,33.6,34.6,34.1,32.8,31.9,32.6,31.6,31.8,30.9)
> output.reg.lin<-lm(y~x)
> output.reg.lin$coefficients
(Intercept)
x
41.3304348
-0.1386957
b) Si valuti con un test opportuno l’esistenza di un legame lineare tra la velocità e il consumo di benzina,
scegliendo α=0,01.
Si tratta di verificare l’ipotesi nulla H0: β1=0 attraverso la statistica test:
tc =
b1
* 2
j
∑ (y − y )
(n − 2)∑ (x − x )
j
2
j
in cui la devianza di dispersione è:
> dev.disp<-sum(output.reg.lin$residuals^2)
[1] 3.147826
la devianza di x è:
> dev.x<-sum((x-mean(x))^2)
[1] 690
mentre b1 è il secondo elemento del vettore output.reg.lin$coefficients e lo si seleziona
mediante
> b1<-output.reg.lin$coefficients[2]
Pertanto la statistica test risulta :
> tc<-b1/sqrt(dev.disp/(8*dev.x))
[1] -5.808006
5
Per verificare l’ipotesi nulla si confronta tale valore con quello teorico ottenuto in corrispondenza
di α=0,01 e di 8 gradi di libertà:
> qt(0.005,8)
[1] -3.355387
Poiché –5.808006 < -3.355387 si rifiuta l’ipotesi nulla. In modo analogo si poteva calcolare il p-value
associato alla statistica test -5.808006. La funzione pt (e così le funzioni pnorm, pbinom, pf ecc.)
calcola l’area della coda della distribuzione t di Student in corrispondenza di due argomenti:
l’ascissa e i gradi di libertà. Pertanto:
> 2*pt(–5.808006,8)
[1] 0.0004014839
ed essendo 0.0004014839<0.01 (=α) si conclude che “o si è verificato un evento molto raro, oppure
l’ipotesi nulla non è vera”. Quindi si rifiuta l’ipotesi nulla di indipendenza lineare tra i consumi e
la velocità.
Agli stessi risultati si poteva arrivare utilizzando la funzione summary applicata all’output di lm.
La funzione produce alcune informazioni di sintesi sulla stima del modello lineare:
> summary(output.reg.lin)
Call:
lm(formula = y ~ x)
Residuals:
Min
1Q
-1.10870 -0.16359
Median
0.07826
3Q
0.36957
Max
0.89783
Coefficients:
Estimate Std. Error t value
(Intercept) 41.33043
1.47013 28.113
x
-0.13870
0.02388 -5.808
--Signif. codes: 0 `***' 0.001 `**' 0.01
Pr(>|t|)
2.77e-09 ***
0.000401 ***
`*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 0.6273 on 8 degrees of freedom
Multiple R-Squared: 0.8083,
Adjusted R-squared: 0.7843
F-statistic: 33.73 on 1 and 8 DF, p-value: 0.0004015
Vi sono elencate informazioni sui residui, sulla verifica di ipotesi dei parametri, sull’indice di
determinazione lineare e sul test F per valutare la significatività del modello di regressione. Con
riferimento alla parte intitolata Coefficients si ritrova la statistica test e il p-value calcolati per la
stima del coefficiente di regressione. L’indice di determinazione lineare R-Squared risulta 0.8083 e
lo si poteva altresì ottenere con i seguenti passaggi:
> dev.tot<-sum((y-mean(y))^2)
> dev.reg<-dev.tot-dev.disp
> dev.reg/dev.tot
[1] 0.8083048
La statistica F, Fc =
Devreg (Y ) 1
s2
= 2reg la si può calcolare anche come:
Devdisp (Y ) (n − 2) sdisp
> dev.reg/(dev.disp/8)
[1] 33.73293
6
Se si vuole visualizzare la tabella dell’analisi della varianza per questo modello di regressione si
può utilizzare il comando anova:
> anova(output.reg.lin)
Analysis of Variance Table
Response: y
Df Sum Sq Mean Sq F value
Pr(>F)
x
1 13.2732 13.2732 33.733 0.0004015 ***
Residuals 8 3.1478 0.3935
--Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
7


![[FORMULARIO] [Per il corso di Data Mining e Statistica per il](http://s1.studylibit.com/store/data/005291898_1-1df697f347fcbd9a0a842a75091c5040-300x300.png)






