A/D dynamic test
A.C. Neve – ITIS “E.Fermi” Lecce
I comportamenti dei sistemi elettronici in regime statico e dinamico risultano spesso così diversi
tra loro tanto da renderne problematico l’utilizzo in molte applicazioni.
La definizione e misura di molti parametri statici può spesso dare l’impressione di poter disporre
di un buon sistema per il trattamento dei segnali.
Nell’utilizzo reale, cioè in condizioni dinamiche, si vengono purtroppo a determinare dei
comportamenti che risultano ben diversi da quelli attesi o dalle specifiche di progetto richieste.
L’incremento di complessità di questi sistemi, rende ancor più problematico il loro controllo ed il
relativo utilizzo come nel caso dei sistemi di conversione dati (A/D).
Un perfetto convertitore A/D dovrebbe essere in grado di fornire una accurata digitalizzazione
del valore che un segnale assume nell’istante di campionamento.
Gli errori che intervengono in regime dinamico sono causati da diversi fattori quali il tempo di
risposta, il settling time e lo slew rate dei dispositivi analogici usati come pure l’incertezza di
apertura (jitter), i codici errati e le non linearità.
Tutti questi fattori concorrono all’insorgere di distorsioni nelle forme d’onda acquisite e quindi, in
errori nell’interpretazione delle informazioni associate.
Risulta pertanto necessario lo sviluppo di tecniche efficienti ed affidabili per il loro rilevamento e
che siano in grado di garantire un buon livello di significatività della misura stessa.
Tra i vari test oggi disponibili, i più diffusi risultano:
il beat frequency testing, l'istogram plot, il sine wave curve fitting e l'FFT plot.
In tutti questi test, il convertitore viene sollecitato con un segnale sinusoidale sia perché
risulta facilmente generabile e con elevata accuratezza, sia perché il suo spettro è
costituito da una singola riga.
Il segnale sinusoidale utilizzato deve necessariamente possedere un elevato grado di
purezza e stabilità, una ampiezza pari al fondo scala dell'A/D in esame ed una frequenza
definibile con grande precisione.
Questi parametri devono poter essere adeguatamente calibrati anche in funzione delle
prestazioni esprimibili dall'A/D sotto test.
Le stesse considerazioni sono ovviamente valide anche per il segnale di campionamento
usato per pilotare l'A/D.
E' consigliabile ricorrere sempre all'uso di generatori sintetizzati i quali sono in grado di
fornire le necessarie garanzie di precisione e stabilità ed eventualmente interporre un
filtro passa basso ad elevata pendenza per attenuare ulteriormente le eventuali
componenti armoniche o segnali indesiderati che possono presentarsi all'ingresso
dell'A/D.
L'uscita dell'A/D fornirà, nel tempo, dei record di dati rappresentativi della codifica del
segnale di ingresso, questi record di dati verranno usati come input per un opportuno
sistema di elaborazione dotato di ben precise caratteristiche hardware-software e
generalmente appartenente alla classe dei microcomputer detti Digital Signal
Processing.
A.C. NEVE – A/D dynamic test
1
Beat frequency test
Questo test fornisce in modo semplice e rapido un'informazione complessiva sulla
qualità dell'A/D in esame non comprensiva però degli errori di offset e di guadagno.
Nella Fig. 1 è visibile uno schema applicativo di questo test.
Il segnale di ingresso dovrà essere in grado di sottoporre l'A/D a delle condizioni
estremali di funzionamento in termini di livelli e velocità, l'uscita verrà poi ricostruita e
visualizzata in real time con l'ausilio di un D/A.
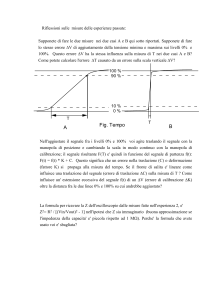
La frequenza del segnale di ingresso dovrà risultare di valore leggermente superiore a
quella del segnale di campionamento, in tal modo la frequenza del segnale ricostruito in
uscita sarà pari alla differenza (∆f) tra le due e quindi molto bassa come si può osservare
dalla Fig. 2, questa soluzione crea anche minori difficoltà nella selezione del D/A.
Fig. 1 – Schema a blocchi del sistema di test
Fig. 2 – Segnali relativi al beat frequency test
Qualsiasi deviazione dell'uscita dalla forma d'onda sinusoidale, sarà indice di presenza
di errori nell'A/D.
Codici errati saranno visualizzati come discontinuità localizzate o come espansioni del
tempo di permanenza di un certo codice.
A.C. NEVE – A/D dynamic test
2
E' opportuno che il processo di acquisizione renda disponibili diversi rilevamenti per
ognuno dei possibili codici dell'A/D in modo da evitare l'insorgere di problemi con il
D/A e rendere più efficiente la visualizzazione.
Affinché ciò sia possibile, è opportuno che la differenza ∆f tra le due frequenze fg=1/Tg
ed fs=1/Ts risulti adeguatamente contenuta.
Il massimo valore assumibile da ∆f può essere determinato richiamando il concetto di
aperture time, il suo legame con la risoluzione dell'A/D e con la frequenza stessa del
segnale di ingresso.
Per poter garantire che ogni codice sia rilevato almeno una volta è necessario che la
differenza tra il periodo del segnale sinusoidale e quello del segnale di campionamento
non sia superiore al valore del tempo di apertura associato a quelle condizioni di
acquisizione o, equivalentemente che, la differenza di livello del segnale tra due
successivi campioni non sia superiore ad 1 LSB nel punto di massima pendenza.
Si ha quindi che:
SLOPE =
∆t =
∆V
d 1
Vpp
Vpp ⋅π
= ( ⋅Vpp ⋅sin( 2⋅π ⋅ fg )
=
⋅ 2 ⋅ π ⋅ fg =
∆t
dt 2
Tg
2
t =0
Vpp
2n
∆V
Tg
=
=
SLOPE Vpp ⋅ π 2 n ⋅ π
Tg
∆f = fg − fs =
∆f =
∆t
1
1
−
=
=
Tg Tg + ∆t Tg ⋅ (Tg + ∆t )
Tg
2n ⋅π
Tg ⋅ (Tg +
Tg
)
2n ⋅π
=
1
Tg ⋅ (1 + 2 n ⋅ π )
fg
fg
≈
1 + 2n ⋅π 2n ⋅ π
Per es., facendo uso di un segnale sinusoidale con frequenza di 5 MHz ed un A/D a 12
bit, il massimo valore di ∆f sarà di circa 380 Hz.
Esempi di calcolo delle frequenze di campionamento
A.C. NEVE – A/D dynamic test
3
Esiste poi una seconda versione di questo test chiamata envelope test.
In questo caso, il segnale di ingresso sarà costituito da una sinusoide avente ampiezza
pari al fondo scala e frequenza di poco superiore alla metà della frequenza del segnale
di campionamento e cioè: fg = ∆f + fs/2.
In queste condizioni l'uscita del D/A può essere considerata come costituita da due
sinusoidi in opposizione di fase e con frequenza ∆f.
Durante l'esecuzione del test, in alcuni casi si può verificare che due successivi
campioni risultino agli estremi dei possibili codici dell'A/D, come nei punti A e B della
Fig. 3, e quindi ottenere significative informazioni circa il comportamento dell'A/D in
alta velocità e, più specificatamente, sul suo settling time; tale indagine non è
espletabile con il test precedente in quanto tutti i campioni risultano avere dei valori tra
loro alquanto prossimi.
Fig. 3 – Segnali relativi all’envelope test
Per ottenere una corretta visualizzazione della forma d'onda è necessario apportare una
leggera modifica all'hardware in modo che soltanto una delle due fasi contribuisca alla
ricostruzione del segnale per mezzo del convertitore D/A di uscita.
A.C. NEVE – A/D dynamic test
4
Histogram plot
Questo test è in grado di fornire utili informazioni sul grado di non linearità
differenziale presentato dall'A/D, sui suoi eventuali codici errati, sull'errore di offset e di
guadagno; non è possibile ottenere informazioni sui parametri dinamici dell'A/D in
esame.
La presenza di picchi di discontinuità nel grafico, è indice di una certa non linearità
differenziale mentre l'assenza di rilevamenti, è indice di presenza di codici errati.
Il test consiste nel campionare in modo random il segnale sinusoidale di ingresso
rilevando un numero di campioni statisticamente significativo e con questi costruire il
diagramma della funzione densità di probabilità ( FDP ), un diagramma cioè che riporti
i valori della frequenza con la quale ogni codice si è verificato in funzione dei possibili
codici.
Il test viene sempre condotto nelle condizioni estremali di funzionamento consentite
dall'A/D sotto misura. E’ anche necessario che la frequenza del segnale di ingresso non
risulti in alcun modo correlata con la frequenza del segnale di campionamento, e cioè
non siano in relazione di multipli o sottomultipli ne legate da divisori comuni.
Nel caso ideale, Fig. 4, il risultato dovrebbe fornire la ben nota funzione di densità di
probabilità di un segnale sinusoidale:
P(v) =
1
π ⋅ V p2 − v 2
con Vp valore di picco della sinusoide.
Nel caso reale, la curva (istogramma) presenta generalmente dei picchi o degli
avvallamenti i quali sono indicativi di un allargamento o una riduzione dell'intervallo
decisionale corrispondente a quel livello di tensione; si rammenta che per un A/D
avente un fondo scale di Vfs volt e risoluzione di n bit, ogni intervallo decisionale
dovrebbe avere una ampiezza costante pari a Vfs/2n volt.
Nella Fig. 5 è visibile l'istogramma relativo ad un A/D commerciale che presenta diversi
punti con elevata non linearità differenziale e dei codici mancanti.
L'entità della non linearità differenziale è espressa dalla relazione:
Diff. NL =
Prob. reale ( codice )
− 1
Prob. ideale( codice )
dipende quindi dal rapporto tra la probabilità reale ed ideale relativa ad uno dei 2n
possibili codici; la probabilità reale è data dal rapporto tra il numero di eventi relativi ad
un certo codice Nc ed il numero totale di campioni rilevati,
P.reale(Nc) =
Nc
NTotSample
A.C. NEVE – A/D dynamic test
5
Fig. 4 – FDP per un segnale sinusoidale
Fig. 5 – Histogram plot per un A/D ad n bit
A.C. NEVE – A/D dynamic test
6
La probabilità ideale è invece data dall'integrale della funzione di probabilità di una
sinusoide relativamente ad un certo codice Nc e risulta:
P.ideale(Nc) =
(
)
(
n −1
1 −1 Vfs ⋅ Nc − 2 n −1
−1 Vfs ⋅ Nc − 1 − 2
⋅ sen
−
sen
π
Vp ⋅ 2 n
Vp ⋅ 2 n
)
Particolarmente importante è il numero di campioni necessari per ottenere un
istogramma con un soddisfacente grado di attendibilità statistica, per A/D con
risoluzione di 8 o 10 bit sono necessari da centomila ai trecentomila campioni, mentre
per A/D con risoluzione di 16 o 18 bit possono anche essere necessari da dieci milioni a
cinquanta milioni di campioni.
Curve fitting
Questo test è in grado di fornire una quantificazione complessiva delle prestazioni
dell'A/D attraverso la misura di un parametro chiamato numero di bit effettivi.
Le sorgenti di errore rilevabili sono attribuibili a varie forma di non linearità quali
distorsione armonica, incertezza di apertura e rumore.
Per contro, non consente la determinazione dell'ampiezza di banda e degli errori di
offset, di guadagno e di fase.
Il test si sviluppa attraverso l'elaborazione di un record di dati ottenuto dal
campionamento del solito segnale sinusoidale applicato all'ingresso dell'A/D.
L'elaborazione consiste nel rigenerare via software il segnale sinusoidale di ingresso
attraverso il best fit del record dei dati.
La differenza tra i valori ottenuti con l'acquisizione del record e quelli della sinusoide
ricostruita attraverso il best fit, rappresenta l'errore residuo descritto in Fig. 6.
La deviazione standard dell'errore così calcolato è poi rapportata all'errore ideale
previsto per l'A/D sotto misura.
Se l'errore riscontrato è più elevato di quello ideale, si può ritenere che il numero di bit
con i quali l'A/D converte è inferiore a quello in effetti dichiarato nelle specifiche.
Il numero di bit effettivi viene definito per mezzo della seguente relazione:
Errore RMS reale
Neff. = n − lon 2
con n = risoluzione dell A/D
Errore RMS ideale
L'errore RMS ideale è dato dall'errore di quantizzazione già in precedenza discusso e
pari a Q/ ( 2 ⋅ 3 ) , con Q che rappresenta l'ampiezza dell'intervallo decisionale
dell'A/D ( Q=Vfs/2n ) ed n pari alla risoluzione dell'A/D.
L'errore RMS reale è invece dato dall'espressione:
Err. RMS reale =
M
∑ [x − V
i
p
⋅ cos(ω ⋅ ti + P ) − C ]
2
i=1
A.C. NEVE – A/D dynamic test
7
Fig. 6 – Errore residuo nel test di curve fitting
con xi e ti che rappresentano il valore e l'istante associato ad ogni campione del record,
Vp, ω, P e C rispettivamente l'ampiezza, la frequenza, la fase e l'offset della sinusoide
ricostruita ed M il numero complessivo di campioni del record.
Variando opportunamente le condizioni di esecuzione del test, è possibile ottenere
anche delle informazioni sugli errori dovuti all'incertezza di apertura ed alla distorsione
armonica.
FFT plot
L'FFT plot è il più diffuso e significativo dei test dinamici oggi disponibili, esso è usato
per caratterizzare le prestazioni di un A/D nel dominio della frequenza e non è in grado
di fornire informazioni sugli errori di offset e di guadagno.
Come al solito, il test è condotto con un ingresso sinusoidale avente ampiezza pari al
fondo scala.
Idealmente, lo spettro dovrebbe essere costituito da una singola riga spettrale, in realtà
l'operazione di campionamento e conversione, attraverso le quali si perviene al calcolo
della FFT, introduce sostanziali differenze.
La trasformata discreta di Fourier è definita dalla seguente relazione:
− J ⋅ 2⋅ π ⋅
1 N −1
⋅ ∑ g(n) ⋅ e
G(fk) =
N n=0
k ⋅n
N
con k indice di frequenza, n indice di campione ed N numero di campioni del record pari
ad una potenza di due.
Lo spettro così ottenuto risulterà discreto in quanto il segnale di ingresso è periodico e
poi limitato in frequenza nell’intervallo 0÷fs/2 in quanto il segnale stesso è campionato
ad intervalli ∆t corrispondenti ad una frequenza di campionamento fs = 1/∆t.
A.C. NEVE – A/D dynamic test
8
L'operatore trasformata discreta di Fourier richiede un record di dati i cui estremi si
raccordino con continuità matematica o, equivalentemente, che il record contenga un
numero intero di periodi della funzione di ingresso.
Non sempre però ciò si verifica e le discontinuità estremali del record introducono un
errore detto leakage.
L'errore di leakage può essere ridotto moltiplicando il record dati per una funzione di
durata pari a quella del record e di andamento tale da lasciare inalterato il record nella
sua parte centrale ma azzerandolo agli estremi ed imponendone così la continuità
cercata.
L'operazione descritta è meglio nota col nome di windowing (finestratura). Si noti che
in generale l'operazione di finestratura introduce comunque una piccola riduzione
dell'ampiezza dello spettro la quale è certamente tollerabile pur di ridurre l'entità del
leakage che renderebbe lo spettro incomprensibile e quindi inutilizzabile.
Diversi sono i tipi di finestre utilizzabili ed ognuna con delle caratteristiche che le
rendono più efficienti a secondo dei casi, le più note sono quella di Hanning, di
Hamming, di Kaiser Bessel e di Blackman Harris.
E' ovvio che la situazione ottimale sarebbe quella di ottenere un record dati continuo ed
evitare così il processo di finestratura.
Una volta fissata la lunghezza del record ed il valore della frequenza di campionamento,
tale condizione si ottiene assegnando alla frequenza della sinusoide di ingresso un
valore tale che il record contenga un numero intero di periodi.
Un metodo pratico è il seguente:
si fissano la frequenza di campionamento fs e la lunghezza N del record, si assegna poi
alla frequenza del segnale un valore, fappr., pari a quello desiderato ma non definitivo
in quanto è da considerarsi approssimativo.
Fig. 7 – FFT plot di un A/D a 10 bit
Si moltiplica per N il rapporto fappr./fs e si arrotonda il risultato al più vicino intero
dispari. Indicando con M questa quantità, la frequenza effettiva da assegnare al segnale
di ingresso è data dal prodotto tra M ed il rapporto fs/N, quindi:
feff. =
fs
fappr.
⋅ Int. Disp. N ⋅
N
fs
A.C. NEVE – A/D dynamic test
9
per es. ponendo fs = 500.000000000 KHz, N = 16384 ed fappr. = 20 KHz si ottiene feff.
= 19.989013671 KHz.
La tecnica appena descritta non è certamente difficile da implementare in quanto in fase
di collaudo di un A/D, si dispone sempre di strumentazione ad elevate prestazioni.
E' ben noto che un processo di campionamento operato a frequenza fs rende disponibile
uno spettro il cui contenuto informativo si estende fino alla frequenza fs/2, se il segnale
acquisito contenesse componenti spettrali superiori ad fs/2, queste verrebbero ripiegate
indietro nell'intervallo 0÷fs/2 causando così errore di aliasing.
Nella Fig. 7 è visibile lo spettro di uscita di un A/D a 10 bit di buona qualità e pilotato
con un segnale di frequenza molto inferiore a quella di campionamento.
Si può notare la presenza di rumore dovuto all'errore di quantizzazione il cui valore è
pari a: SNR = (6.02⋅n + 10.8)dB. Più elevata è la risoluzione, più piccolo sarà l'errore di
quantizzazione e quindi più basso il livello medio di rumore.
Nella Fig. 8 è invece visibile lo spettro dell'uscita di un A/D a 16 bit pilotato con un
segnale avente ancora frequenza molto inferiore a quella di campionamento ed affetto
da una leggera non linearità la quale è evidenziata dalla presenza di armoniche a
frequenza multipla della fondamentale ed ampiezza sufficientemente contenuta.
Nella Fig. 9 è infine visibile lo spettro dell'uscita dello stesso convertitore pilotato però
con un segnale di frequenza molto prossima a quella di campionamento, si può notare
che le componenti a frequenza multipla della fondamentale sono state ripiegate
all'indietro con valori più bassi della fondamentale stessa.
Questo fenomeno viene tollerato ed adeguatamente gestito, per poter effettuare misure
alle frequenza limite.
In questo caso la scelta della frequenza del segnale di ingresso dovrebbe essere tale da
evitare l'addensamento delle varie righe spettrali intorno alla fondamentale e
consentirne un suo chiaro rilevamento.
Il comportamento ora descritto è dovuto al fenomeno dell'intermodulazione che si
verifica quando due segnali vengono ad interagire in un sistema non lineare (come il
S/H) e produce sull'uscita dei prodotti di intermodulazione dovuti a somma e differenza
tra le varie armoniche dei segnali interagenti.
La distorsione di intermodulazione, DIM, è definita come:
DIM = 10 ⋅ log
Somma dei valori eff. di IM (fino al 3° ordine)
Valore eff. del segnale utile
Nella tabella seguente sono riportati i valori assunti dalle varie armoniche per un
segnale campionato con fs = 2MHz:
Fondamentale
2° armonica
3° armonica
4° armonica
5° armonica
6° armonica
7° armonica
980 KHZ
40 KHz
940 KHz
80 KHZ
900 KHz
120 KHZ
860 KHz
950
100
850
200
750
300
650
KHz
KHz
KHz
KHz
KHz
KHz
KHz
900
200
700
400
500
600
300
KHz
KHz
KHz
KHz
KHz
KHz
KHz
850 KHz
300 KHz
550 KHz
600 KHz
250 KHz
900 KHz
50 KHz
Prodotti di intermodulazione
A.C. NEVE – A/D dynamic test
10
Fig. 8 – FFT di un A/D commerciale a 16 bit
Fig. 9 – Aliasing nella FFT di un A/D a 16 bit
Gli effetti combinati dell'errore di quantizzazione, della distorsione armonica, di segnali
spuri che possono interagire col sistema di misura e di eventuali fenomeni di
intermodulazione, possono agire sul valore del rapporto segnale rumore e
sull'andamento dello spettro di frequenza dell'A/D.
Un valore del rapporto segnale rumore inferiore a quello ideale è certamente indicativo
della presenza di errori nell'A/D.
A.C. NEVE – A/D dynamic test
11
Fig. 10 – FFT di un A/D a 10 bit con alta non linarità
Nella Fig. 10 è visibile il risultato di una FFT su un A/D ad 8 bit affetto da una elevata
non linearità complessiva.
Per ottenere una FFT significativa è necessario curare opportunamente alcuni delicati
aspetti:
il record dati dovrebbe avere una lunghezza non inferiore a 1024÷2048 per A/D con
bassa risoluzione, fino a 65536 per A/D ad alta risoluzione in modo da garantire che,
tutti i possibili codici siano testati e venga contenuta la generazione complessiva di
rumore, si può infatti osservare una riduzione del rumore di 3 dB per ogni duplicazione
della lunghezza del record.
Per risoluzioni medio basse, i tradizionali sistemi di calcolo a 32 bit con aritmetica in
floating point possono ancora risultare soddisfacenti ma per alti valori di risoluzione, al
fine di poter preservare l'ampio range dinamico disponibile, sono consigliati sistemi di
calcolo a 64 bit con coprocessore matematico e supportati da compilatori efficienti ed
algoritmi di calcolo ottimizzati e veloci.
La tabella successiva propone una sintesi dei test descritti.
A.C. NEVE – A/D dynamic test
12
Errore
Histogram plot
FFT plot
Si
–
Presenza
di
Si
–
Presenza
di
Non linearità
spikes
su
alcuni
elevato
rumore
di
Differenziale
Si – Elevato valore
di errore RMS
Curve fitting
Si
Beat frequency
Missing code
Si – Elevato valore
di errore RMS
Si
Si – Elevato valore
di errore RMS
Si
Si – Elevato valore
di errore RMS
No
codici
Si – Presenza di
codici a conteggio
nullo
Si – Misurabile con
una rampa lineare
fondo
Si – Presenza di
elevato rumore di
fondo
Si – Presenza di
armoniche
Rumore
No
Si – Elevato valore
di errore RMS
No
Ampiezza
di banda
Errore di
guadagno
Errore di
offset
No
Si – Presenza di
elevato rumore di
fondo
Si – Presenza di
elevato rumore di
fondo
No
No
Si
Si
No
No
No
Si
No
No
No
Non linearità
integrale
Incertezza di No
apertura
Bibliografia
1) J.Sherwin - Specifing A/D and D/A convert - Application Note 156
National Semiconductor Co. 1976.
2) Hnatek - A user's handbook of A/D and D/A converts Ed J. Wiley & Sons
3) D.F. Hoeschele - Analog to digital and digital to analog conversion tecniques –
Ed. J. Wiley & Sons.
4) D.H. Sheingold - Analog digital conversion notes by Engineering Staff of Analog Devices Inc.
5) E. Zuch - Data acquisition and conversion handbook - 1979
Ed. Datel Sys. Inc.
6) The handbook of linear I.C. applications - 1987 - Burr Brown Co.
7) Fundamentals of Sampled Data System – AN 282 – Analog Devices
8) Dynamic performance testing of A to D converts Product Note 5180A-2 - Hewlett Packard.
9) Peetz Neil Muto - Measuring waveform recorder performance Hewlett Packard Journal - Nov. 1982 p21.
10) The fundamentals of signal analysis Hewlett Packard - Application Note 243 - Feb. 1985.
11) Dynamic tests for A/D convert performance Burr Brown - Application Note AN 133 - 1985.
12) An introduction to the Samplig Theorem – AN236 – National Semicon.
13 A.C. Neve – Introduzione al digital signal processing –
Ed. Schonenfeld &Ziegler (Mi) - 2002
A.C. NEVE – A/D dynamic test
13