1) Un corpo di massa m1= 1 kg di muove su un piano orizzontale

CORSO DI LAUREA IN SCIENZE BIOLOGICHE
II Prova in itinere di FISICA – 21 Giugno 2007
1) Una lamina piana infinita uniformemente carica con densità superficiale
 = + 2 10-12 C/m2 si trova a distanza h=2m da una carica positiva Q,
posta nell' origine O del sistema di assi cartesiani, come mostrato in figura.
Nel punto di coordinate A = (1m, 0) viene posta una carica q = + 10-12 C.
Determinare:
a) il campo elettrico prodotto dalla lamina nel punto ove si trovano
le cariche Q e q (specificandone modulo direzione e verso) ed il valore
della carica Q tale che la carica q si trovi all'equilibrio nel punto A;
b) il lavoro totale delle forze elettrostatiche per spostare la carica q dal punto
A=(1m.0) al punto B=(1m,1m).

y
B=(1m,1m)
Q
O
q
A=(1m,0)
x
[N.B. 0 = 8.85 10-12 C2/Nm2]
2) Un cubetto di lato L= 10 cm , è costituito di materiale plastico, che ha densità d = 1.2 g /cm3 . All’interno del
cubetto si trova una cavità sferica, concentrica , di raggio incognito.
Sapendo che il peso del cubetto è 8 N, si determini:
a) il raggio della cavità sferica;
b) la tensione di una fune, fissata sul fondo di un recipiente pieno di acqua, a cui viene legato il cubetto in modo
da risultare, all’equilibrio, totalmente immerso nell’acqua.
3) Una mole di gas perfetto biatomico, che si trova inizialmente nello stato termodinamico
(PA=105 Pa, VA= 3 10-2 m3,TA), compie il ciclo termodinamico composto dalle seguenti trasformazioni:
AB: espansione isoterma fino al volume VB=2VA,
BC: decompressione isocora fino alla pressione PC = ¼ PB,
CD: compressione isobara fino al volume VD= VA,
DA: compressione isocora fino alla pressione iniziale.
Il candidato svolga i seguenti punti:
a) si disegni il ciclo sul piano p-V e si determinino le variabili P,V e T nei punti A,B,C e D;
b) si calcolino il lavoro compiuto ed il calore scambiato dal gas nelle quattro trasformazioni e si valuti
il rendimento del ciclo;
c) facoltativo: si confronti il rendimento del ciclo con quello di un analogo ciclo che utilizzi gas perfetto
monoatomico e con quello di un ciclo di Carnot che lavori tra le temperature minime e massime.
SCRIVERE IN MODO CHIARO. GIUSTIFICARE BREVEMENTE I PROCEDIMENTI.
SOSTITUIRE I VALORI NUMERICI SOLO ALLA FINE. NON SCORDARE LE UNITA` DI MISURA.
Testi, soluzioni ed esiti alle pagine: fisbio.webhop.net (AD, EN), www.mi.infn.it/~sleoni (OZ)
SOLUZIONE ESERCIZIO 1
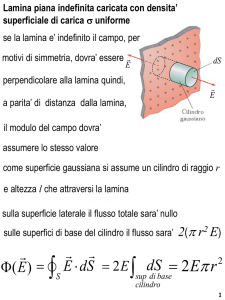
a) La lamina piana infinita produce un campo elettrico uniforme e perpendicolare alla lamina stessa, con verso
uscente dalla lamina, essendo la lamina carica positivamente.
Il campo vale in modulo E 

2  10 12 C / m 2

 0.11 N / C
2 0 2  8.85  10 12 C 2 / Nm 2
Nella regione di spazio a sinistra della lamina, ove si trovano le cariche Q e q, il campo vale quindi:


 
E
i  0.11 N / C i
2 0
La carica q, posta a distanza d da Q, sarà in equilibrio se le forze elettrostatiche prodotte dalla carica Q e dalla
distribuzione piana sono uguali in modulo, ossia:
qQ

q
2
40 d
2 0
1
Q


2
40 d
2 0
1
da cui si ottiene il valore di Q:
Q  (40 ) 

1
N
d2 
 0.11  (1m) 2  0.012  10 9 C  12 pC
9
2
2
2 0
C
9  10 Nm / C
b) Il lavoro totale fatto dalle forze elettrostatiche è dato dalla somma del lavoro LQ fatto dalla forza di Coulomb
generata dalla carica Q e dal lavoro Ldovuto alla forza elettrostatica prodotta dalla lamina piana.
Quest’ultimo è identicamente nullo lungo il percorso AB, essendo la forza sempre perpendicolare allo
spostamento.
Pertanto:
Ltot  LQ  L
 LQ  U  U A  U B

qQ 1 1
(  )
40 rA rB
 (9  10 9 Nm 2 / C 2 )(10 12 C  12 10 12 C )(
 31.6  10 15 J
1
1

)
1m
2m
SOLUZIONE ESERCIZIO 2
a) Se non ci fosse la cavità, la massa del cubetto risulterebbe di 1.2 kg ( L 3 d ), ed il peso 11.76 N.
Poiché il peso è solo 8 N , il peso mancante corrisponde ad una massa di 0.384 kg ed a un volume di 320 cm3 .
Poiché il volume della sfera è dato da Vsfera = 4/3  R3 , il raggio della cavità sferica risulta R=4.24 cm .
b) Quando il cubetto è immerso in acqua agiscono la forza Peso e la tensione T della fune, verso il fondo del
recipiente e la spinta archimedea S , verso l’alto . All’equilibrio la risultante delle forze è nulla , pertanto
S-P-T = 0 . Poiché S è il peso di un cubo di acqua di 10 cm di lato , cioè 9.8 N, risulta T = 1.8 N
SOLUZIONE ESERCIZIO 3
a) TA= PA VA / R ≈ 361 K
VB=2 VA, PB = ½ PA, TB=TA
VC=VB = 2 VA, PC = ¼ PB = 1/8 PA, TC=¼TB =¼ TA
VD=VA, PD = PC = 1/8 PA, TD=1/8 TA
b) AB: QAB = n R TA Ln VB/VA = RTA Ln 2 ≈ 2079 J
LAB = QAB ≈ 2079 J
BC: LBC = 0
QBC = n Cv (TC-TB) = - n Cv ¾ TA = -15/8 RTA = - 5625 J
CD: LCD = PC (VD-VC) = - 1/8 PA VA = - 1/8 RTA = - 375 J
QCD = n Cp (TD-TC) = - 1/8 n Cp TA = - 7/16 RTA = -1312.5 J
DA: LDA = 0
QDA = n Cv (TA - TD) = 7/8 n Cv TA = 35/16 RTA = 6562.5 J
LTOT = LAB+ LCD = 1704 J QTOT = LTOT = 1704 J
QASS = QAB + QDA = 8641.5 J Rendimento ≈ 19.7 %
c) FACOLTATIVO :
Nel caso in cui il gas sia monoatomico, il lavoro svolto dal gas non cambia, mentre il calore
assorbito viene ad essere modificato, in quanto CV = 3/2 R, da cui segue che
QDA = n Cv (TA - TD) = 7/8 n Cv TA = 21/16 RTA = 3937.4 J
QASS = QAB + QDA ~ 6016 J
Il rendimento del ciclo vale quindi :
 = LTOT/QASS ~1704 J/ 6016 J ~ 28.3 %
Nel caso di un ciclo di Carnot che operi tra le temperature minime e massime del ciclo precedente il
rendimento vale:
 = 1 Tmin/Tmax = 1  TD/TA = 1  1/8 = 7/8 = 0.875 ~ 88 %