CAPITOLO 2
LE EQUAZIONI CIRCUITALI
2.1
Introduzione
Il quadro del modello circuitale è, almeno per quanto concerne i circuiti di bipoli,
a questo punto, completo. Esso è così costituito dai:
•
Concetti fondamentali:
- l’intensità della corrente elettrica che attraversa il bipolo;
- la tensione elettrica del bipolo;
•
Leggi fondamentali:
- legge di Kirchhoff per le correnti;
- legge di Kirchhoff per le tensioni;
•
Relazioni caratteristiche.
Tutto ciò che d’ora in avanti si dirà sarà stretta conseguenza di questo “quadro”.
Nel Capitolo 4 faremo vedere che questo quadro si estende naturalmente, senza
alcuna difficoltà e limitazione, ai circuiti che contengono componenti con più di
due terminali.
In un circuito il funzionamento di ogni singolo bipolo è, in ogni istante,
determinato dalla interazione tra il bipolo stesso e il resto del circuito. In altre
parole, si può dire che esso è il frutto della interazione tra due diverse esigenze:
che il bipolo si comporti in modo compatibile con la sua specifica natura e che
106
tale comportamento sia a sua volta compatibile con quello di tutti gli altri bipoli
presenti nel circuito.
Le relazioni caratteristiche descrivono il funzionamento dei singoli bipoli del
circuito e le leggi di Kirchhoff ne regolano l’interazione. Le equazioni che ne
derivano sono le equazioni circuitali. Esse sono l’oggetto del nostro studio. In
particolare, studieremo le proprietà fondamentali di queste equazioni e i loro
metodi di soluzione.
Le equazioni di Kirchhoff, che dipendono solo da come gli elementi circuitali
sono collegati tra loro e non dalla loro specifica natura, sono algebriche lineari
e omogenee.
Le equazioni caratteristiche, che dipendono solo dalla natura fisica dei singoli
elementi del circuito e non da come sono tra loro collegati, possono essere,
invece, di diverso tipo, a seconda della natura fisica dei componenti che esse
descrivono: ad esempio, algebriche lineari, algebriche non lineari, differenziali
lineari, differenziali non lineari. Quindi, la soluzione delle equazioni di un
circuito presenta difficoltà che dipendono non solo dal numero di elementi
presenti e dal modo in cui essi sono collegati, ma anche dalla loro natura.
I circuiti possono essere classificati in due grandi categorie: circuiti resistivi e
circuiti dinamici.
Un circuito si dice resistivo se è costituito da soli generatori e resistori (lineari e
non lineari), cioè da elementi adinamici.
Un circuito si dice dinamico se, oltre a generatori e a resistori, contiene anche
elementi dinamici come, ad esempio, induttori e condensatori. L’ordine di un
circuito dinamico è, per definizione, il numero di bipoli dinamici presenti nel
circuito. Ad esempio, un circuito dinamico del primo ordine è un circuito con
un solo bipolo dinamico, ad esempio, un condensatore o un induttore; un
circuito dinamico del secondo ordine è un circuito con due bipoli dinamici, ad
esempio un condensatore e un induttore, o due condensatori, o due induttori; e
così via.
Allo scopo di illustrare i possibili tipi di equazioni circuitali, le difficoltà che si
incontrano nel loro studio e i metodi di soluzione più importanti, nel prossimo
paragrafo studieremo quattro circuiti, topologicamente semplici1 , in cui sono
presenti alcuni tra gli elementi circuitali più frequentemente utilizzati nelle
applicazioni: i primi due sono resistivi e i restanti sono circuiti dinamici del
primo ordine. I primi tre circuiti che considereremo sono composti da soli tre
1 La topologia di un circuito concerne le proprietà del circuito di bipoli che dipendono dal
modo in cui i bipoli sono tra loro collegati e non la loro specifica natura fisica.
G. Miano, Introduzione ai Circuiti
107
bipoli, connessi in serie. L’ultimo caso che analizzeremo è un circuito
composto da quattro elementi: due bipoli collegati in serie a un parallelo
composto da altri due bipoli.
Nella restante parte del capitolo, invece, studieremo le proprietà delle equazioni
circuitali derivanti unicamente dalla struttura peculiare delle equazioni di
Kirchhoff. Attraverso queste proprietà è possibile affrontare e risolvere i
problemi che nascono dalla complessità delle equazioni circuitali dovuta al
numero di bipoli presenti e al modo in cui essi sono tra loro collegati. In
particolare, faremo vedere come si rappresentano le connessioni di un generico
circuito tramite un grafo. Ciò renderà possibile una trattazione formale delle
equazioni di Kirchhoff, delle loro proprietà di indipendenza, del teorema di
conservazione delle potenze elettriche e del teorema di Tellegen (questi sono
teoremi fondamentali della teoria dei circuiti). Inoltre, introdurremo il concetto
di potenziale di nodo e il concetto di corrente di maglia e le formulazioni delle
equazioni circuitali che su di essi si basano .
Come faremo vedere nel Capitolo 4, tramite i grafi è possibile trattare gli
elementi con più di due terminali allo stesso modo in cui si tratta un
convenzionale elemento con due terminali.
2.2
Circuito resistivo lineare “semplice”
In questo paragrafo e nei prossimi tre, attraverso quattro esempi, evidenzieremo
le tipologie più importanti di equazioni che si incontrano nella soluzione di
circuiti. Ciascuno di essi esemplifica una classe di circuiti di particolare
interesse teorico e applicativo.
L’obiettivo principale di questa esemplificazione è sostanzialmente quello di
cominciare a familiarizzare con la soluzione delle equazioni circuitali, iniziando
a risolvere circuiti “semplici” (e significativi) e poi, man mano, proseguendo
con circuiti sempre più complessi. In questo modo faremo anche una prima
rassegna dei metodi matematici che si utilizzano per la soluzione delle
equazioni circuitali.
Considereremo prima un circuito resistivo lineare, poi un circuito resistivo non
lineare, poi un circuito dinamico lineare tempo invariante con generatore
costante, poi lo stesso circuito dinamico con generatore sinusoidale e, infine, un
circuito dinamico tempo invariante non lineare.
G. Miano, Introduzione ai Circuiti
108
Un circuito resistivo lineare è un circuito costituito da resistori lineari e da
generatori ideali (più in generale da elementi adinamici lineari). Si consideri,
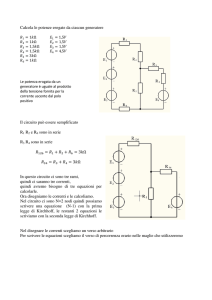
ad esempio, il circuito illustrato in Figura 2.1a. Esso è costituito da due
resistori lineari, di resistenze R1 e R2 , connessi in serie. Due bipoli sono
connessi in serie, se sono gli unici bipoli incidenti allo stesso nodo. La serie di
due resistori è collegata, a sua volta, a un generatore indipendente di tensione.
Questo è l’esempio significativo più semplice di circuito resistivo lineare. Si
determinino le intensità di corrente e le tensioni del circuito e la potenza
elettrica erogata dal generatore di tensione.
+
1
e(t )
R1
R2
v3
v1
i1 R i2
1
e(t ) R2
i3
(a)
2+
v2
3−
(b)
Fig. 2.1 (a) Esempio di circuito resistivo lineare; (b) corrispondente “circuito orientato”.
Il circuito è costituito da tre bipoli e da tre nodi. Le incognite sono le tre
intensità di corrente i1 , i2 , i3 e le tre tensioni v1 , v2 , v 3 . Ricordate, la prima
operazione che bisogna effettuare quando si imposta la soluzione di un circuito
è assegnare i versi di riferimento per le intensità di corrente e le tensioni. È una
buona regola adottare per ciascun bipolo del circuito la stessa convenzione, ad
esempio, quella dell’utilizzatore. Di conseguenza, una volta stabiliti, ad
esempio, i versi di riferimento per le intensità di corrente, sono
automaticamente fissati anche i versi di riferimenti per le tensioni (e viceversa).
Si fissino i riferimenti per i versi delle intensità di corrente così come è indicato
in Figura 2.1b, e si adoperi per ciascun bipolo la convenzione dell’utilizzatore.
In realtà, la tensione del generatore di tensione, a differenza dell’intensità di
corrente, non è incognita, anche se, almeno formalmente, qualche volta
conviene considerarla come tale.
Dopo che sono stati definiti i versi di riferimento, si possono determinare le
equazioni del circuito. Si determinino prima le equazioni di Kirchhoff.
Applicando la legge di Kirchhoff per le correnti al nodo “1” e al nodo “2”
otteniamo:
G. Miano, Introduzione ai Circuiti
109
i1 − i3 = 0 ,
−i1 + i2 = 0 .
(1)
(2)
L’equazione di Kirchhoff per il nodo “3” è −i2 + i3 = 0 , ovvero
i2 − i3 = 0 .
(3)
Quest’ultima equazione non contiene ulteriori informazioni oltre a quelle già
contenute nelle equazioni (1) e (2). Infatti, l’equazione (3) può essere ottenuta
sommando membro a membro le equazioni (1) e (2). Come si usa dire,
l’equazione (3) è una combinazione lineare delle equazioni (1) e (2), ovvero le
equazioni (1), (2) e (3) sono linearmente dipendenti 2 . Di conseguenza non c’è
bisogno di considerare l’equazione (3) nello studio del circuito in esame. È
evidente che non c’è nessun motivo particolare per cui tra le tre equazioni (1),
(2) e (3) scegliamo di usare le prime due e ignoriamo la terza. Potremmo,
ovviamente, usare la prima e la terza e ignorare la seconda, oppure usare la
seconda e la terza e ignorare la prima.
Dalle equazioni (1) e (2) abbiamo immediatamente che
i1 = i2 = i3 .
(4)
Le intensità di corrente nei tre bipoli sono uguali perché sono collegati in serie
(se i versi di riferimento sono quelli scelti in Figura 2.1; otterremmo lo stesso
risultato se cambiassimo i versi di riferimento di tutte e tre le intensità di
corrente).
2 L’equazione f (x1 , x 2 ,...,x n ) = b si dice lineare se f (x1 , x 2 ,...,x n ) è una funzione lineare delle
variabili x1 , x2 ,..., xn , cioè se f (x1 , x 2 ,...,x n ) = α1 x1 + α 2 x 2 + ... + α n xn , dove α 1 ,α 2 ,...,α n sono
coefficienti che non dipendono dalle variabili x1 , x2 ,..., xn ; b è una grandezza nota
indipendente dalle variabili x1 , x2 ,..., xn . Un’equazione lineare è omogenea quando il termine
noto è uguale a zero. Si consideri l’insieme delle m equazioni lineari e omogenee
f j ( x1 ,x 2 ,..., xn ) = α j1 x1 + α j 2 x 2 + ... + α jn xn = 0, con j = 1,2,...,m . Le equazioni di questo
insieme si dicono linearmente dipendenti se e solo se esiste almeno un insieme di m di
costanti, k1 ,k2 ,...,km (almeno due di esse devono essere diverse da zero), tali che
∑
k j f j ( x1 , x2 ,..., xn ) = 0 per ogni x1 , x2 ,..., xn . L’equazioni di questo insieme si dicono si
dicono linearmente indipendenti se e solo se non sono linearmente dipendenti.
m
j =1
G. Miano, Introduzione ai Circuiti
110
Siccome i tre bipoli del circuito sono collegati in serie, il circuito in esame ha
una sola maglia. Orientiamo la maglia in verso orario e applichiamo la legge di
Kirchhoff per le tensioni. Abbiamo:
v1 + v2 + v3 = 0 .
(5)
Ora dobbiamo considerare le equazioni caratteristiche dei bipoli del circuito,
facendo attenzione al fatto che abbiamo usato la convenzione dell’utilizzatore
per ciascun bipolo. Esse sono:
v1 − R1i1 = 0,
v 2 − R2 i2 = 0,
v3 = −e .
(6)
(7)
(8)
Nell’equazione caratteristica del generatore di tensione compare il segno meno
perché il verso di riferimento della tensione v3 è, per come è stato scelto,
opposto al verso di riferimento della tensione e impressa dal generatore di
tensione.
Le equazioni (1), (2), (5), (6), (7) e (8) sono le equazioni del circuito in esame:
esse sono sei equazioni algebriche lineari, linearmente indipendenti, nelle sei
incognite i1 , i2 , i3 e v1 , v2 , v 3 . La soluzione di questo sistema è semplice, basta
applicare il metodo della riduzione per sostituzione o metodo di Gauss.
Sostituendo le espressioni di v1 , v 2 e v3 date dalle equazioni (6), (7) e (8)
nell’equazione (5) abbiamo
R1i1 + R2 i2 − e = 0.
(9)
Utilizzando le relazioni (4), dall’equazione (9) si ha
( R1 + R2 )i1 = e .
(10)
Questa è un’equazione algebrica lineare 3 nell’incognita i1 . La sua soluzione è
3 L’equazione f (x ) = b (b è una grandezza nota, quindi indipendente dalla grandezza
incognita x ) si dice algebrica se f (⋅) è una funzione della variabile x . L’equazione algebrica
f (x ) = b si dice lineare se f (x ) è una funzione lineare della variabile x , cioè f (x ) = Kx dove
K è una costante.
G. Miano, Introduzione ai Circuiti
111
i1 =
e
.
R1 + R2
(11)
Utilizzando, ora, le (6) e (7), dalla (11) si ha
v1 =
R1
R2
e , v2 =
e.
R1 + R2
R1 + R2
(12)
Per determinare la potenza elettrica erogata dal generatore di tensione, p(ge ) ,
consideriamo l’intensità della corrente elettrica i3′ che attraversa il generatore,
definita con il verso di riferimento concorde, in base alla convenzione del
generatore, con quello della tensione v3 . E’ immediato che
i3′ = −i3 .
(13)
Allora, si ha
(e )
pg
e2
= i3′ v3 = −i3 v3 = i3 e =
.
R1 + R2
(14)
Si osservi che i versi di riferimento dell’intensità di corrente e della tensione
impressa e sono in accordo con la convenzione del generatore. Si assuma che la
tensione del generatore ideale di tensione sia, ad esempio, periodica,
e(t ) = E0 + E m cos(ωt) ,
(15)
e che i valori dei parametri del circuito siano quelli riportati in Tabella 2.1. (La
pulsazione ω è legata alla frequenza f dalla relazione ω = 2πf .)
R1 = 1Ω
R2 = 2Ω
E0 = 1V
Em = 3V
f = 1 kHz
Tab. 2.1 Parametri del circuito riportato in Fig. 2.1
Otteniamo
i1 (t ) = i2 (t ) = i3 (t ) =
1
+ cos(ωt) A ,
3
(16)
G. Miano, Introduzione ai Circuiti
112
1
v1 (t ) = + cos(ωt) V ,
3
2
v2 (t) = + 2cos(ωt ) V,
3
(17)
(18)
1
pg(e ) (t ) = (1 + 3cosωt)2 W = 5,5 + 6cosωt + 4,5cos2ωt W,
3
(19)
dove ω = 2π ⋅10 3 s −1 . Si osservi che l’espressione della potenza istantanea
erogata dal generatore contiene un termine costante, uno sinusoidale a
pulsazione ω e uno a pulsazione 2ω .
Problema
Si determinino le intensità di corrente, le tensioni e la potenza elettrica erogata
dal generatore di corrente del circuito resistivo semplice rappresentato in Figura
2.2.
♦
j (t )
Fig. 2.2
2.3
R1
R2
Esempio di circuito resistivo lineare.
Circuito resistivo non lineare “semplice”
La soluzione di un circuito resistivo lineare si riduce sempre alla soluzione di
un sistema di equazioni algebriche lineari. Un qualsiasi sistema di equazioni di
questo tipo può essere risolto analiticamente, ad esempio, utilizzando il metodo
della riduzione per sostituzione, come abbiamo appena fatto vedere. Se il
circuito contiene resistori non lineari bisogna risolvere, invece, un sistema di
equazioni costituito, oltre che da equazioni algebriche lineari, anche da
equazioni algebriche non lineare, tante quanti sono i bipoli non lineari presenti
nel circuito. Ad eccezione di pochissimi casi, la soluzione di equazioni
algebriche non lineari (o di sistemi) non può essere effettuata per via analitica.
G. Miano, Introduzione ai Circuiti
113
Questa è la prima complicazione dovuta alla presenza di elementi non lineari.
Inoltre, può anche accadere che un circuito resistivo non lineare abbia più di
una soluzione o, addirittura, non abbia soluzioni. I circuiti resistivi lineari
hanno sempre una sola soluzione (se si escludono casi molto particolari).
L’esempio che considereremo consentirà di mettere in evidenza tutto ciò in un
modo estremamente semplice.
In questo paragrafo illustreremo due metodi approssimati di soluzione di
equazioni algebriche non lineari: il metodo grafico e il metodo di NewtonRaphson.
Un circuito resistivo è non lineare se contiene resistori non lineari. Si consideri,
ad esempio, il circuito riportato in Figura 2.3a. Esso è costituito da un resistore
lineare di resistenza R , da un resistore non lineare e da un generatore ideale di
tensione costante. Siccome i tre bipoli sono collegati in serie, l’intensità delle
correnti elettriche che li attraversano sono uguali, così come abbiamo mostrato
nel circuito esaminato in precedenza. Per questa ragione nel disegno riportato in
Figura 2.3a è riportata solo l’intensità della corrente i , con il corrispondente
verso di riferimento. In conseguenza di ciò non dobbiamo considerare le
equazioni di Kirchhoff per le correnti.
+
+
v1
i
i
i
+
R1
E
v2
−
−
(a)
Fig. 2.3
v2
(b)
v2
(c)
(a) Esempio di circuito resistivo non lineare; due esempi di curve caratteristiche
tipiche di resistori non lineari: (b) diodo a giunzione pn, (c) diodo tunnel .
Studieremo il circuito in esame considerando due tipi di resistori non lineari: il
resistore non lineare con curva caratteristica monotona crescente del tipo
riportato in Figura 2.3b (potrebbe essere la curva caratteristica di un diodo a
giunzione pn), e il resistore non lineare con curva caratteristica non monotona
del tipo riportato in Figura 2.3c (potrebbe essere la curva caratteristica di un
diodo tunnel). Entrambe le curve caratteristiche possono essere descritte da
G. Miano, Introduzione ai Circuiti
114
un’equazione algebrica non lineare del tipo (in entrambi i casi il resistore non
lineare è controllato in tensione)
i2 = g(v 2 ) ,
(20)
dove g(v 2 ) è una funzione a un solo valore.
Applicando la legge di Kirchhoff per le tensioni all’unica maglia del circuito
abbiamo (orientiamo la maglia in verso orario)
v1 + v2 − E = 0;
(21)
E è il valore della tensione del generatore. Infine dalla relazione caratteristica
del resistore lineare abbiamo l’equazione
v1 − R1i = 0.
(22)
Combinando l’equazione (22) con l’equazione (21) si ottiene
R1i + v 2 = E .
(23)
Siamo giunti, così, al sistema di due equazioni
R1i + v 2 = E,
i − g v = 0,
( 2)
(24)
nelle due incognite i e v 2 . Il sistema di equazioni (24) è un particolare sistema
ridotto delle equazioni del circuito in esame. Esso è un sistema di due equazioni
algebriche una delle quali è non lineare.
Sostituendo l’espressione di i in funzione di v 2 , che si ottiene dalla prima
equazione del sistema (24), nella seconda equazione, si ha l’equazione algebrica
non lineare 4
4
L’equazione f (x ) = b si dice algebrica se f (⋅) è una funzione della variabile x . L’equazione
algebrica f (x ) = b si dice non lineare se e solo se f (x ) è una funzione non lineare della
variabile x , come, ad esempio, x 2 , x , log( x ), e x .
G. Miano, Introduzione ai Circuiti
115
v2
+ g(v2 ) = E ,
R1
(25)
nell’incognita v 2 . Anche se avessimo scelto di ridurre il sistema (24) a una sola
equazione nell’incognita i avremmo ancora ottenuto un’equazione non lineare.
Come già abbiamo osservato, solo in casi molto particolari è possibile risolvere
esattamente, attraverso metodi analitici, le equazioni algebriche non lineari. In
generale bisogna ricorrere a metodi di soluzione approssimati.
2.3.1 Metodo grafico
Il sistema (24) può essere sempre risolto per via grafica.
Il metodo per la ricerca della soluzione consiste nel riportare la retta R
descritta dall’equazione lineare (equazione (23)) sul piano (v2 ,i ) in cui è
tracciata la curva caratteristica G del resistore non lineare (equazione (20)),
come illustrato in Figura 2.4.
Osservazione
La retta R , che in letteratura prende il nome di retta di carico, descrive il
funzionamento del bipolo costituito dalla serie generatore di tensione resistore: essa è la curva caratteristica di questo bipolo concorde con la
convenzione del generatore.
♦
Al variare del valore della resistenza R1 varia la pendenza della retta di carico
(per fissato valore di E ), mentre al variare della tensione E impressa dal
generatore la retta trasla parallelamente a se stessa (per fissato valore di R1 ),
Figura 2.4.
Le intersezioni della retta di carico R con la curva caratteristica del resistore
non lineare G individuano dei punti, detti punti di lavoro. I valori di intensità
di corrente e tensione, che rappresentano le coordinate di questi punti, (V2 , I) ,
sono soluzioni del sistema (24), e quindi, soluzioni del circuito. Infatti, le
coppie di tensione - corrente (v2 ,i ) associate ai punti della retta R sono, per
costruzione, soluzioni della prima equazione del sistema (24); le coppie di
tensione - corrente (v2 ,i ) associate ai punti della curva G sono, per costruzione,
G. Miano, Introduzione ai Circuiti
116
soluzioni della seconda equazione del sistema (24). Di conseguenza, le coppie
(V2 , I ) corrispondenti ai punti di lavoro, siccome appartengono a entrambe le
curve, verificano entrambe le equazioni del sistema (24) e, quindi, sono
soluzioni del circuito.
In Figura 2.4 sono riportate le soluzioni, ottenute in questo modo, del circuito
di Figura 2.2 corrispondenti alle due curve caratteristiche riportate in Figura
2.2b e Figura 2.2c.
Nel primo caso la curva caratteristica del resistore non lineare è monotona e
strettamente crescente, nel secondo caso la curva caratteristica non è monotona
in un tratto limitato, dove presenta un massimo e un minimo relativi.
Quando la curva caratteristica è monotona crescente si ha sempre una e una sola
intersezione tra la retta di carico e la curva caratteristica del resistore non
lineare, e quindi una e una sola soluzione (Figura 2.4a).
Quando la curva caratteristica non è monotona, invece, è anche possibile, per
opportuni valori della tensione del generatore, avere tre intersezioni e quindi tre
soluzioni (Figura 2.4b). Se la pendenza della retta è, in valore assoluto,
sufficientemente elevata, la retta interseca la curva caratteristica sempre in un
solo punto, indipendentemente dal valore di E , anche quando la curva
caratteristica non è monotona, Figura 2.4c.
i
i
E = E3
E = E2
E = E1
R
G
i
E1 < E2 < E3
G
I
R3
V2
v2
(a)
Fig. 2.4
G
R2
(b)
R1
v2
v2
(c)
R1 R2 R3
(a) La retta di carico R interseca sempre in un solo punto la curva G ; (b) la retta
di carico può intersecare in tre punti la curva G non monotona; (c) la retta di
carico interseca in un solo punto la curva G non monotona.
Soffermiamoci sul caso in cui ci sono più soluzioni. Cosa significa che un
circuito ha più soluzioni? Dal punto di vista matematico è un fatto normale che
un’equazione non lineare ammetta più di una soluzione (oppure nessuna
G. Miano, Introduzione ai Circuiti
117
soluzione); quando una equazione non lineare ammette una e una sola soluzione
è, in realtà, un caso molto particolare. Dal punto di vista fisico, invece, è un
assurdo. Infatti, il circuito che potremmo realizzare in laboratorio, collegando
in serie un generatore di tensione, un resistore e un diodo tunnel avrà un
comportamento deterministico. Il fatto è che il circuito rappresentato in Figura
2.3a è solo un modello approssimato del corrispondente “circuito fisico”. Il
circuito fisico, a parità di tensione impressa dal generatore, può raggiungere
uno stato di equilibrio invece che un altro a seconda della sua storia, per la
presenza di fenomeni dinamici di natura capacitiva nel diodo tunnel, fenomeni
che sono assenti nel modello del diodo considerato nel circuito di Figura 2.3. In
conclusione, per poter determinare quale soluzione si realizza effettivamente nei
circuiti resistivi che ammettono più di un punto di lavoro, non si possono
ignorare i fenomeni dinamici presenti nei resistori non lineari con curve
caratteristiche non monotone. Ritorneremo su questa questione nell’esempio
sviluppato nel § 2.5.
I circuiti con più punti di lavoro sono molto importanti nelle applicazioni, essi
sono alla base dei circuiti bistabili.
2.3.2 Metodo di Newton Raphson
Il metodo grafico che abbiamo appena illustrato può fornire soltanto soluzioni
molto approssimate (l’errore, ad esempio, introdotto dallo spessore della punta
della matita con cui tracciamo la curva caratteristica e la retta di carico). Per
ottenere soluzioni accurate è necessario ricorrere a metodi approssimati di tipo
numerico.
Il metodo di Newton-Raphson rappresenta il metodo approssimato più
comunemente usato per risolvere le equazioni di circuiti resistivi non lineari e
consente di raggiungere elevati gradi di precisione. Di seguito sono riportati i
concetti essenziali di questo metodo applicandolo al circuito in esame nel caso
in cui esso ha una sola soluzione.
Riscriviamo l’equazione (25) come
F (v2 ) = 0 ,
(26)
dove
G. Miano, Introduzione ai Circuiti
118
F (v2 ) ≡ g(v 2 ) +
v2 − E
.
R1
(27)
Si consideri la curva F nel piano (v2 , y ) definita dall’equazione
y = F (v 2 ) .
(28)
La soluzione dell’equazione (26) è l’ascissa V2 del punto di intersezione tra la
curva F e l’asse delle ascisse, Figura 2.5.
Il metodo di Newton-Raphson è un metodo iterativo 5 . Si sceglie un valore
iniziale arbitrario v (20) e si genera una successione di valori v (21) , v2(2 ) , v2(3 ) ,... che,
come vedremo, tende alla soluzione V2 . La regola con cui questa successione
viene generata è illustrata graficamente in Figura 2.5. Il valore iniziale v (20)
potrebbe essere, ad esempio, la soluzione dell’equazione ottenuta ignorando i
termini non lineari nell’equazione (26).
y
F
R0
R1
( 2)
(1)
V2 v 2 v 2
R2
Fig. 2.5
v (20)
v2
Descrizione grafica del metodo di Newton-Raphson.
Una volta scelto il valore di v (20) , si tracci, prima, la retta R 0 tangente alla
(
( ))
curva F nel punto v2(0 ) , F v (20 ) , poi si determini l’intersezione di questa retta
con l’asse delle ascisse, e infine, si assuma l’ascissa di questo punto come valore
per v (21) . Si ripeta tale procedimento, tracciando la retta R 1 tangente alla curva
5 Isac Newton introduce l’idea (1666) per risolvere l’equazione: x 3 − 2x − 5 = 0 ; l’idea è resa
“più” algoritmica da Raphson (1690).
G. Miano, Introduzione ai Circuiti
119
(
( ))
F nel punto v2(1 ) , F v2(1) , determinando poi l’ascissa del punto di intersezione
di questa retta con l’asse delle ascisse e assumendo infine questa ascissa come
valore per v (22) , e così via. In Figura 2.5 è riportata una sequenza
v (21) , v2(2 ) , v2(3 ) ,... generata attraverso questa procedura. È evidente come essa
converga naturalmente verso la soluzione V2 dell’equazione (26).
Quale è il significato di questa procedura dal punto di vista matematico?
Al passo h + 1 ( h = 0,1, 2,...) dell’algoritmo di Newton-Raphson si approssima
la curva F con la retta R h tangente alla curva F nel punto v2(h ) , F v (2h) , che è
(
( ))
descritta dall’equazione
( )(
) ( )
y (h +1) = F ′ v(2h ) v2(h +1) − v2(h ) + F v2(h ) ;
(29)
con il simbolo F ′ indichiamo la derivata prima della funzione F (v2 ) rispetto a
v 2 . La soluzione (di tentativo) v (2h+1) si ottiene imponendo che
y (h +1) = 0 ;
(30)
v (2h+1) è l’ascissa del punto di intersezione della retta R h con l’asse delle ascisse
(ricordiamo che la soluzione esatta è l’ascissa del punto di intersezione della
curva F con l’asse delle ascisse). Ciò equivale a sostituire, al generico passo h
della procedura, l’equazione non lineare (26) con l’equazione lineare
( )(
)
( )
F ′ v2(h ) v2(h +1) − v2(h ) + F v2(h ) = 0 ,
(31)
la cui soluzione è
( h+1)
v2
(h )
= v2
F(v2(h ) )
−
;
F ′ (v2(h ) )
(32)
La formula (32) è la formula iterativa dell’algoritmo di Newton-Raphson. Essa
è applicata ripetutamente finché la grandezza F v (2n) , detto residuo
( )
dell’equazione (26), non diventi più piccola (o al limite uguale) di un valore
prefissato che sta a indicare l’errore massimo ammissibile nella soluzione del
problema in esame. In principio, l’iterazione dovrebbe essere continuata fino a
G. Miano, Introduzione ai Circuiti
120
quando il residuo si annulla; in pratica ciò è irrealizzabile perché sono
necessarie un numero infinito di iterazioni. Anche se ciò fosse possibile, non
avrebbe, ovviamente, nessun importanza dal punto di vista fisico, perché non è
possibile misurare e controllare le grandezze fisiche con una precisione
illimitata.
Tab. 2.2
( )
n
v (2h)
F v (2n)
0
1/3
1/3
1
5/18
0.0262...
2
0.272616...
0.0001985...
3
0.272577...
0.000000011...
Metodo di Newton-Raphson applicato all’equazione 9v 32 + 3v2 − 1 = 0 .
Si consideri il caso in cui il circuito di Figura 2.3a abbia R1 = 1Ω, E = 1V e
g(v2 ) = 2v2 + 9v23 . La funzione F (v2 ) vale
F (v2 ) = 9v23 + 3v2 − 1.
(33)
Si scelga v (20) = 1/3; questo valore è la soluzione dell’equazione che si ottiene
ignorando il termine non lineare nell’equazione (33), cioè è la soluzione
dell’equazione 3v2 −1 = 0 . I risultati dell’iterazione, che converge rapidamente
verso la soluzione, sono riportati in Tabella 2.2.
y
F
V2
V∗
Fig. 2.6
v2
Il metodo di Newton-Raphson non converge se V ∗ è il valore iniziale di tentativo.
La convergenza del metodo di Newton-Raphson è sempre assicurata quando la
funzione F (v2 ) è strettamente crescente. Nel caso illustrato in Figura 2.6, caso
che si verifica quando la curva caratteristica del resistore non lineare è non
G. Miano, Introduzione ai Circuiti
121
monotona, la convergenza dipende dal valore che si sceglie per il tentativo
iniziale. Se si scegliesse V * come valore iniziale si avrebbe una sequenza
oscillante, e quindi la procedura non convergerebbe verso la soluzione V2 . Si
osservi che anche in questo caso l’equazione ha una sola soluzione.
2.4 Circuiti dinamici del primo ordine “semplici”, lineari e tempo
invarianti
Abbiamo già detto che i circuiti che contengono resistori, generatori e bipoli
dinamici, come induttori e condensatori, prendono il nome di circuiti dinamici.
I circuiti dinamici costituiti da un solo elemento dinamico - un induttore o un
condensatore - prendono il nome di circuiti dinamici del primo ordine.
Ricordiamo che l’ordine sta a indicare il numero di elementi dinamici presenti
nel circuito.
In questo paragrafo vengono studiati i due circuiti del primo ordine illustrati in
Figura 2.7; sia l’induttore che il condensatore sono lineari e tempo invarianti.
Questi sono i circuiti del primo ordine più semplici.
Le equazioni che descrivono i due circuiti hanno la forma di un’equazione
differenziale di primo ordine lineare. Come vedremo nel Capitolo 3 e
approfonditamente nel Capitolo 5 un generico circuito del primo ordine lineare
può essere sempre ricondotto allo studio di un circuito del tipo illustrato in
Figura 2.7.
+
+
v1
i
+
+
R
e
v1
i
+
L
v2
R
C
−
(a)
Fig. 2.7
+
v2
e
−
−
−
(b)
(a) Un circuito dinamico del primo ordine con condensatore; (b) un circuito
dinamico del primo ordine con induttore.
In entrambi i circuiti i bipoli sono in serie, e quindi, le intensità di corrente che
li attraversano sono uguali, così come abbiamo già visto nei due circuiti
resistivi esaminati precedentemente. Per questa ragione negli schemi riportati in
G. Miano, Introduzione ai Circuiti
122
Figura 2.7 è indicata solo l’intensità della corrente i , con il corrispondente
verso di riferimento. In conseguenza di ciò, anche questa volta non dobbiamo
considerare le equazioni di Kirchhoff per le correnti.
Consideriamo il circuito di Figura 2.7a. Applicando la legge di Kirchhoff per le
tensioni all’unica maglia del circuito otteniamo (la maglia è orientata in verso
orario)
v1 + v2 − e (t ) = 0 .
(34)
Ora dobbiamo utilizzare le equazioni caratteristiche del resistore e del
condensatore. Dalla relazione caratteristica del resistore lineare abbiamo
l’equazione
v1 − R1i = 0,
(35)
mentre dall’equazione caratteristica del condensatore lineare tempo invariante
abbiamo l’equazione
i −C
dv2
= 0.
dt
(36)
All’equazione differenziale (36) bisogna affiancare, per una descrizione
completa del comportamento del condensatore, e quindi del circuito, il valore
della tensione del condensatore, che è la grandezza di stato del circuito,
all’istante iniziale,
v2 (t = 0 ) = V0 .
(37)
Le equazioni (34)-(36), insieme alla condizione iniziale (37), descrivono
completamente la dinamica del circuito in esame; le grandezze incognite sono
tre, v1 , v 2 e i . Queste equazioni sono tutte lineari, ma una di esse è
un’equazione differenziale. Questa è la difficoltà introdotta dalla presenza di un
elemento dinamico, come il condensatore.
Il sistema di equazioni (34)-(36) può essere ridotto ad una sola equazione
differenziale in cui l’incognita è la grandezza di stato v2 . Questa è la procedura
di riduzione più semplice, perché la grandezza di stato è la grandezza che
appare sotto l’operazione di derivata nell’unica equazione differenziale del
sistema di equazioni del circuito.
G. Miano, Introduzione ai Circuiti
123
Sostituendo nell’equazione (35) l’espressione di i data dall’equazione (36), e
l’espressione di v1 , così ottenuta, nell’equazione (34), si ha l’equazione per la
tensione del condensatore
RC
dv2
+ v2 = e(t ) .
dt
(38)
Questa è un’equazione differenziale del primo ordine, lineare, a coefficienti
costanti: “differenziale” significa che la funzione incognita v2 compare anche
sotto l’operatore di derivata; “di ordine uno” significa che compare un termine
proporzionale alla derivata prima di v2 e che non compaiono termini
proporzionali alle derivate di ordine superiore; “lineare” perché l’espressione a
primo membro dipende linearmente dalla funzione incognita v2 (t) ; “a
coefficienti costanti” perché i coefficienti che moltiplicano la derivata prima
della funzione v2 e la funzione v2 non derivata (rispettivamente, RC e 1) sono
indipendenti dal tempo. Il termine indipendente da v2 (t) , a secondo membro
dell’equazione (38), è il termine noto. In questo caso coincide con la tensione
impressa dal generatore e, in generale, può variare nel tempo.
L’equazione (38) ha infinite soluzioni. Per determinare quella che
effettivamente si ha nel circuito in esame bisogna imporre che la soluzione
verifichi anche la condizione iniziale (37).
Il prodotto RC ha le dimensioni di un tempo e, quindi, i tre termini
dell’equazione (38) sono tutti omogenei dimensionalmente con una tensione 6 .
Osservazione
Anche per le altre grandezze del circuito è possibile determinare le equazioni
che esse devono verificare. L’equazione per la tensione v1 è
RC
dv1
de
+ v1 = RC .
dt
dt
(39)
Questa equazione può essere ottenuta a partire dall’equazione (38) utilizzando
la relazione (34).
6 La derivata di una funzione omogenea dimensionalmente con una tensione è una grandezza
omogenea dimensionalmente con V ⋅s−1 .
G. Miano, Introduzione ai Circuiti
124
Utilizzando la relazione (35), dall’equazione (39) si ottiene immediatamente
l’equazione per l’intensità della corrente i ,
RC
di
de
+i = C .
dt
dt
(40)
Le equazioni (38), (39) e (40) differiscono solo per il termine noto (e per
l’incognita): i termini a sinistra di queste equazioni hanno tutti la stessa forma e
sono moltiplicati per gli stessi coefficienti. Questo fatto non è casuale, ma è una
proprietà generale dei circuiti lineari. Essa è una diretta conseguenza del fatto
che, pur essendo le grandezze incognite diverse, esse sono grandezze elettriche
di bipoli che interagiscono perché appartengono allo stesso circuito.
Anche le equazioni (39) e (40) devono essere risolte con opportune condizioni
iniziali. Come facciamo a determinarle ?
E’ molto semplice. L’equazione (34) vale per ogni istante di tempo e, quindi,
anche all’istante t = 0. Di conseguenza si ha
v1 (0) = e(0 ) − v2 (0) .
(41)
Utilizzando la condizione iniziale (38) si ottiene
v1 (0) = e(0 ) − V0 .
(42)
Questo è il valore della tensione del resistore all’istante iniziale.
Per determinare il valore iniziale dell’intensità della corrente elettrica, i(0) ,
utilizziamo l’equazione (35), anche essa vale per ogni istante di tempo e,
quindi, anche all’istante t = 0. Si ha
i(0) =
v1 (0)
.
R
(43)
Utilizzando la (42), si ottiene per i(0)
i(0) =
G. Miano, Introduzione ai Circuiti
e(0) − V0
.
R
(44)
125
Non possiamo utilizzare l’equazione (36) perché non conosciamo il valore della
derivata prima della tensione del condensatore all’istante iniziale !!!
L’equazione (36) consente di valutare proprio dv2 /dt all’istante iniziale una
volta noto il valore iniziale dell’intensità di corrente. Abbiamo trovato un
risultato molto interessante: i valori di tutte le grandezze del circuito all’istante
t = 0 dipendono solo dal valore della tensione del generatore (che è nota) e
dalla condizione iniziale della tensione del condensatore (della grandezza di
stato, che è nota). Le relazioni che esprimono le grandezze elettriche del
circuito all’istante t = 0 in funzione del valore iniziale della tensione del
generatore e del valore iniziale della grandezza di stato del circuito sono tutte di
tipo algebrico. Questa è una proprietà generale e vale per ogni istante di tempo.
Comunque una volta determinata la soluzione dell’equazione (38) che verifica
la condizione iniziale (37) non c’è bisogno di risolvere le equazioni (39) e (40)
con le condizioni iniziali (42) e (44), rispettivamente, per determinare la
tensione v1 e l’intensità della corrente i . Una volta nota la tensione v2 ,
attraverso le relazioni (34) e (35) si determinano direttamente la tensione v1 e
l’intensità della corrente i .
♦
Esercizio
Si verifichi che l’intensità della corrente elettrica i , che attraversa l’induttore
nel circuito di Figura 2.7b, è soluzione dell’equazione
L
di
+ Ri = e (t ) .
dt
(45)
Questa equazione deve essere risolta con la condizione iniziale
i( t = 0 ) = I 0 .
(46)
L’intensità della corrente i è la grandezza di stato del circuito. Per le altre
grandezze del circuito valgono considerazioni simili a quelle appena svolte per
l’altro circuito. Lasciamo al lettore lo sviluppo di queste considerazioni.
♦
G. Miano, Introduzione ai Circuiti
126
2.4.1 Evoluzione libera e scarica del condensatore (dell’induttore)
Ora analizzeremo in dettaglio due tipi di evoluzioni, estremamente importanti
sia dal punto di vista concettuale che da quello applicativo.
Cominciamo ad analizzare una situazione estremamente interessante, cioè quella
in cui (il generatore di tensione è spento)
e(t ) = 0 .
(47)
A differenza di quanto accade nei circuiti resistivi, nei circuiti dinamici, come,
ad esempio, quelli di Figura 2.7, le tensioni e le intensità delle correnti sono
diverse da zero anche quando i generatori sono spenti, o sono assenti, se le
condizioni iniziali sono diverse da zero.
+
v1
i
+
R
+
v1
+
L
v2
R
C
v2
−
(a)
Fig. 2.8
i
−
(b)
(a) Circuito RC in evoluzione libera; (b) circuito RL in evoluzione libera.
Un circuito dinamico si dice che è in evoluzione libera se è privo di generatori,
o se i generatori che contiene sono tutti spenti, Figura 2.8. Nei circuiti in
evoluzione libera l’energia immagazzinata all’istante iniziale nei bipoli
conservativi (condensatore, induttore) produce le correnti del circuito.
L’energia elettrica dissipata dai resistori è, in questi casi, proprio quella
immagazzinata inizialmente nei bipoli conservativi.
L’evoluzione libera del circuito di Figura 2.7a (cioè l’evoluzione del circuito
RC di Figura 2.8a) è descritta dall’equazione differenziale omogenea
RC
G. Miano, Introduzione ai Circuiti
dv2
+ v2 = 0 ;
dt
(48)
127
“omogenea” significa che il termine noto è uguale a zero. Essa deve essere
risolta con la condizione iniziale (37). Riscriviamo l’equazione (48) nella
forma:
dv2
v
=− 2 .
dt
RC
(49)
Le soluzioni dell’equazione (49) sono tutte quelle funzioni le cui derivate sono,
a meno del fattore costante −1/ RC , che ha le dimensioni di s −1 , uguali alla
funzione stessa. Quali sono queste funzioni?
Dal corso di Analisi Matematica sappiamo che la funzione esponenziale
g( x ) = e x
(50)
ha una proprietà di questo tipo. Infatti, si ha
d x
e = ex .
dx
(51)
È evidente che e t non è la soluzione dell’equazione (49), perché la derivata di
e t è proprio uguale a se stessa. Questo non è un problema, basta modificarla
semplicemente. Si consideri la funzione f (t ) così definita:
f (t ) = e λt ,
(52)
dove λ è un parametro per il momento arbitrario, dimensionalmente omogeneo
con l’inverso di un tempo 7 . Per questa funzione si ha che
d λt
e = λe λt .
dt
(53)
Allora, se si sceglie
λ= −
1
,
RC
(54)
7 L’argomento di una qualsiasi funzione del tempo, ad eccezione di quelle di tipo lineare o
lineare affine, deve essere necessariamente un numero puro, quindi la grandezza fisica che
esso rappresenta deve essere adimensionale.
G. Miano, Introduzione ai Circuiti
128
si ottiene
d λt
1 λt
df
1
e =−
e , ovvero,
=−
f.
dt
RC
dt
RC
(55)
Allora, se è verificata la condizione (54) la funzione (52) è soluzione
dell’equazione (49). A questo punto osserviamo che, se la funzione f (t ) è una
soluzione dell’equazione (49), anche la funzione Af (t) , dove A è una costante
arbitraria, è soluzione della stessa equazione. Questa proprietà è solo
conseguenza del fatto che l’equazione (48) è lineare e omogenea.
Al parametro λ , dimensionalmente omogeneo con l’inverso di un tempo, si dà
il nome di “frequenza naturale” del circuito. L’aggettivo naturale sta a indicare
il fatto che il valore di λ dipende solo dai parametri R e C del circuito.
Siccome sia R che C sono positivi, la frequenza naturale del circuito RC è
negativa.
In conclusione, l’espressione dell’integrale generale dell’equazione (48) è
v2 (t) = Aexp (−t / τ) ,
(56)
dove
τ=−
1
= RC .
λ
(57)
Il parametro τ è dimensionalmente omogeneo con un tempo e prende il nome
di costante di tempo del circuito; la costante arbitraria A prende il nome di
costante di integrazione.
L’espressione (56) al variare del valore della costante A nell’intervallo
(−∞, +∞) descrive la famiglia di funzioni che verificano l’equazione (48).
Questa famiglia rappresenta la soluzione generale dell’equazione (48). Tra tutte
le possibili soluzioni descritte dalla (57) quella compatibile con la condizione
iniziale (37) è la soluzione del circuito. Per determinarla basta imporre che la
funzione (57) all’istante t = 0 verifichi la condizione iniziale (37). Imponendo
la condizione (37) si ottiene per la costante A
A = V0 .
G. Miano, Introduzione ai Circuiti
(58)
129
Infine, sostituendo la (58) nella (57) si ottiene la soluzione effettiva del circuito
in esame
v2 (t) = V0 exp(−t /τ ) .
(59)
L’andamento dell’intensità della corrente elettrica è
i( t) =
V0
exp(−t /τ ) .
R
(60)
Siccome la costante di tempo τ è positiva sia la tensione del condensatore che
l’intensità della corrente elettrica tendono esponenzialmente a zero, qualunque
sia il valore di V0 . Il condensatore, dunque, si scarica.
Esercizio
Il lettore verifichi che l’energia inizialmente immagazzinata nel condensatore
viene trasformata interamente in calore durante il processo di scarica,
2
∞ v ( t)
1
2
CV0 = ∫0 2 dt .
2
R
(61)
♦
Si consideri il grafico della tensione del condensatore. In Figura 2.9 viene
riportato la curva per il caso in cui V0 = 1V , R = 1Ω e C = 1mF; la costante di
tempo è τ = 1ms . Valgono le seguenti proprietà:
-
La retta passante per i due punti (0,V0 ) e (τ, 0) del piano (t, v2 ) è tangente
alla curva della tensione v2 (t) nel punto (0,V0 ) .
Dopo un intervallo di tempo pari a una costante di tempo τ il valore della
tensione è, approssimativamente, il 63% del valore iniziale V0 ,
v2 ( τ) ≅
63
V .
100 0
(62)
G. Miano, Introduzione ai Circuiti
130
-
Dopo un intervallo pari a cinque costanti di tempo, il valore della tensione
è, approssimativamente, il 7‰ del valore iniziale V0 ,
7
v2 (5τ ) ≅
V .
(63)
1000 0
-
Dopo un intervallo pari a dieci costanti di tempo, il valore della tensione è,
approssimativamente, 45 /1000000 volte il valore iniziale V0 ,
v2 (10τ) ≅
45
V .
1000000 0
(64)
V2 [V]
1,2
V0 = 1 V
1
0,8
0,6
0,4
0,2
0
0
Fig. 2.9
τ=1ms
1
2
3
4
5
6 t [ms]
Tensione del condensatore durante la scarica di un circuito RC.
È evidente, allora, il significato fisico della costante di tempo τ . Essa dà una
misura dell’intervallo di tempo necessario affinché il condensatore si scarichi.
In principio è richiesto un tempo infinito per la scarica completa del
condensatore. In realtà, dopo un intervallo di tempo pari a un numero finito ma
elevato di costanti di tempo (ad esempio, cinque o dieci) il condensatore si può
ritenere “praticamente” scarico. Anche se la tensione è diversa da zero, ad
esempio, dopo cinque costanti di tempo, nell’applicazione di interesse può
essere ritenuta praticamente uguale a zero, perché, ad esempio, è molto più
piccola della tensione associata al rumore termico o del valore minimo di
tensione che lo strumento di misura è in grado di rilevare.
G. Miano, Introduzione ai Circuiti
131
Esercizio
Si verifichi che l’intensità della corrente elettrica i che attraversa l’induttore
del circuito di Figura 2.7b in evoluzione libera (del circuito RL di Figura 2.8b)
è
i(t) = I0 exp (−t / τ) ,
(65)
dove
τ=
L
R
(66)
è la costante di tempo del circuito RL. In un circuito RL in evoluzione libera
l’induttore si scarica con la costante di tempo data dall’espressione (66).
Il lettore verifichi, anche, che l’energia inizialmente immagazzinata
nell’induttore viene trasformata interamente in calore nel resistore durante il
processo di scarica,
∞
1 2
LI 0 = ∫0 Ri 2 (t )dt .
2
(67)
♦
2.4.2 Evoluzione generica ed evoluzione forzata
Si consideri, ora, la situazione più generale in cui la tensione del generatore del
circuito di Figura 2.7a è diversa da zero. Bisogna, ora, determinare la soluzione
generale dell’equazione differenziale (38), che è non omogenea.
La soluzione generale di un’equazione differenziale è l’espressione che
rappresenta tutte le possibili soluzioni dell’equazione. Siccome l’equazione (38)
è lineare, la sua soluzione generale v2 (t) può essere sempre rappresentata
attraverso la somma,
v2 (t) = v0 (t ) + v p (t) ,
(68)
G. Miano, Introduzione ai Circuiti
132
di una qualsiasi soluzione v p (t ) dell’equazione (38), che denomineremo
soluzione particolare dell’equazione (38), e della soluzione generale v0 (t)
dell’equazione omogenea associata,
RC
dv0
+ v0 = 0.
dt
(69)
È immediato verificare che l’espressione (68) è soluzione dell’equazione (38),
basta sostituirla in essa.
La soluzione particolare v p (t ) dell’equazione (38) dipende dal termine noto
dell’equazione e, quindi, non può essere determinata se non si specifica la
funzione e(t ).
La soluzione generale dell’equazione omogenea associata (69) la conosciamo:
l’abbiamo determinata quando abbiamo studiato l’evoluzione libera del circuito
RC. Essa è
v0 (t) = Aexp (−t / τ) ,
(70)
dove τ è la costante di tempo del circuito RC, la cui espressione è data dalla
(57), e A è una costante arbitraria (la costante di integrazione). Pertanto,
l’espressione dell’integrale generale dell’equazione (37) è
v2 (t) = Aexp (−t / τ) + v p (t ) .
(71)
Al variare della costante di integrazione A si hanno tutte le possibili soluzioni
del circuito in esame. Tra tutte le possibili soluzioni descritte dalla (71) quella
che effettivamente si ha nel circuito in esame è quella compatibile con la
condizione iniziale (37). Per determinarla basta imporre che la funzione data
dall’espressione (71) all’istante t = 0 verifichi la condizione iniziale (37).
Imponendo la condizione (37) si ottiene per la costante A
A = V0 − v p (t = 0 ) .
(72)
Infine, sostituendo la (72) nella (71) si ottiene la soluzione effettiva del circuito
in esame
G. Miano, Introduzione ai Circuiti
133
[
]
v(t ) = V0 − v p (t = 0) exp( −t /τ ) + v p (t) .
(73)
In presenza di generatori l’espressione della soluzione è costituita da due
termini. Il primo termine tende esponenzialmente a zero, qualunque sia il
valore iniziale della tensione, con la costante di tempo τ . Pertanto, per t → ∞
la tensione del condensatore tende asintoticamente all’andamento descritto dalla
soluzione particolare.
Si dice che un circuito è in evoluzione forzata se le grandezze di stato del
circuito all’istante iniziale sono tutte nulle (la tensione del condensatore e
l’intensità di corrente dell’induttore) e, quindi, l’energia inizialmente
immagazzinata in essi è uguale a zero. In evoluzione forzata le intensità di
corrente del circuito vengono prodotte solo attraverso l’azione dei generatori.
Allora, per definizione, la soluzione del circuito di Figura 2.7a in evoluzione
forzata è
v(t ) = −v p (t = 0) exp(−t / τ ) + v p (t ) .
(74)
In questo caso la costante di integrazione dipende solo dal valore della
soluzione particolare all’istante t = 0.
Esercizio
Si verifichi che l’espressione dell’intensità della corrente elettrica i che
attraversa l’induttore del circuito di Figura 2.7b è, in generale,
[
]
i(t) = I0 − ip (t = 0) exp( −t /τ ) + ip (t) ,
(75)
dove la costante di tempo τ data dalla relazione (66), ip (t ) è una soluzione
particolare dell’equazione (45) e I0 è il valore iniziale dell’intensità della
corrente elettrica che attraversa l’induttore. La soluzione in evoluzione forzata è
i(t) = −ip (t = 0 )exp( −t / τ) + i p (t ) .
(76)
♦
G. Miano, Introduzione ai Circuiti
134
Resta ancora da determinare una soluzione particolare dell’equazione (38).
Come abbiamo già fatto notare, per determinare una soluzione particolare c’è
bisogno di specificare la tensione impressa dal generatore di tensione.
Diciamo subito che, in generale, non è possibile determinare analiticamente una
soluzione particolare per qualsiasi andamento temporale della tensione e(t ) del
generatore. Qui di seguito studieremo due casi, come poi vedremo sono molto
importanti nelle applicazioni, in cui è possibile determinare analiticamente una
soluzione particolare: prima il caso in cui e(t ) è una funzione costante e poi
quello in cui è una funzione sinusoidale.
2.4.3 Generatore stazionario e carica del condensatore (dell’induttore)
Si consideri, prima, il caso in cui la tensione del generatore di tensione sia
costante,
e(t ) = E0 .
(77)
Bisogna determinare una soluzione particolare dell’equazione
RC
dv2
+ v2 = E0 .
dt
(78)
Essendo il termine noto e i coefficienti dell’equazione (78) costanti nel tempo è
presumibile che essa abbia una soluzione costante nel tempo,
v p (t ) = V .
(79)
Sostituendo la (79) nella (78) e ricordando che la derivata di una costante è
uguale a zero, si ottiene
v p (t ) = E0 .
(80)
Questa è la soluzione stazionaria del circuito. In conclusione, la soluzione
generale dell’equazione (78) è
v2 (t) = Aexp (−t / τ) + E 0 .
(81)
Imponendo la condizione iniziale (37) si ha la soluzione effettiva del circuito,
G. Miano, Introduzione ai Circuiti
135
v2 (t) = (V0 − E )e −t τ + E0 .
(82)
Questa è la soluzione del circuito nel caso di generatore stazionario. Qualunque
sia il valore della condizione iniziale abbiamo
v2 (t) → E0 per t → ∞ .
(83)
Il primo termine dell’espressione (82) tende esponenzialmente a zero,
qualunque sia il valore iniziale della tensione, con la costante di tempo τ . Ad
esso si dà il nome di termine transitorio. Dopo che il transitorio si è estinto, la
soluzione del circuito è quella stazionaria. Per tale ragione alla soluzione
stazionaria (80) si dà il nome di soluzione di regime stazionario del circuito. Si
osservi che il termine transitorio dipende dalla condizione iniziale, mentre
quello di regime è indipendente dalla condizione iniziale.
In Figura 2.10 sono riportati gli andamenti della tensione del condensatore per
due valori diversi della condizione iniziale (e per lo stesso valore della tensione
del generatore): E0 = 1V , R = 1Ω e C = 1 mF ; la costante di tempo è τ = 1ms e
il valore di regime della tensione è E0 = 1 V .
v2 [V]
1,2
1
0,8
V0=0
0,6
0,4
V0=0,5 V
τ=1 ms
0,2
0
0
Fig. 2.10
1
2
3
4
5
6
t [ms]
Andamenti della tensione del condensatore corrispondenti a due condizioni
iniziali diverse.
G. Miano, Introduzione ai Circuiti
136
v2
E0
τ
Fig. 2.11
t
Carica di un circuito RC.
L’evoluzione forzata del circuito di Figura 2.7a con generatore costante
descrive il processo di carica di un condensatore. L’andamento nel tempo della
tensione del condensatore durante la carica è descritta dalla funzione
v2 (t) = E 0 (1 − e −t / τ ) ;
(84)
il grafico è rappresentato in Figura 2.11.
♦
La retta passante per i due punti (0,0 ) e (τ, E 0 ) del piano (t, v2 ) è tangente alla
curva della tensione nel punto (0,0 ) . Dopo un intervallo di tempo pari, ad
esempio, a cinque volte la costante di tempo, possiamo ritenere praticamente
carico il condensatore. La differenza, in valore assoluto, tra il valore della
tensione all’istante t = 5τ e il valore di regime stazionario è,
approssimativamente, il 7‰ rispetto al valore di regime,
v2 (5τ ) − E0 ≅
7
E .
1000 0
L’intensità della corrente elettrica che attraversa il circuito è data da
G. Miano, Introduzione ai Circuiti
(85)
137
i( t) =
E 0 −t /τ
e .
R
(86)
L’intensità della corrente elettrica tende a zero esponenzialmente per t → ∞ ; il
massimo valore, che assume all’istante t = 0, vale
Imax =
E0
.
R
(87)
Per assegnata capacità, il processo di carica è tanto più veloce quanto più
piccola è il valore della resistenza. Di conseguenza i processi di carica veloci
sono caratterizzati da elevate intensità di corrente nella parte iniziale del
processo. Nelle applicazioni il tempo di carica di un condensatore è
determinato, per fissato valore della capacità, proprio dal valore massimo
dell’intensità di corrente elettrica che può attraversare il circuito senza sia
danneggiato.
L’energia elettrica assorbita dal resistore durante il processo di carica è
∞
w R (0, ∞) = ∫0
E02
CE02
Ri (t)dt =
τ=
.
2R
2
2
(88)
Di conseguenza l’energia erogata dal generatore di tensione ideale durante
l’intero processo di carica è
CE02 CE02
w e (0,∞) = w R (0, ∞) + wC (0, ∞) =
+
= CE02 .
2
2
(89)
Quindi metà dell’energia erogata dal generatore è dissipata sotto forma di
calore e metà è immagazzinata nel condensatore. Questo è un risultato generale,
indipendente dai valori effettivi dei parametri del circuito.
♦
Esercizio
L’evoluzione forzata del circuito di Figura 2.7b con generatore stazionario
descrive il processo di carica di un induttore. Si verifichi che l’andamento nel
G. Miano, Introduzione ai Circuiti
138
tempo dell’intensità della corrente elettrica che attraversa l’induttore è descritta
dalla funzione
i( t) =
E0
1 − e −t / τ ) ,
(
R
(90)
dove la costante di tempo τ è data dalla relazione (66). Valgono considerazioni
simili a quelle appena svolte per la carica del condensatore. Lasciamo al lettore
il loro sviluppo.
♦
2.4.4 Generatore sinusoidale
Si consideri, ora, il caso in cui la tensione impressa dal generatore di tensione
sia sinusoidale nel tempo con pulsazione ω (ω = 2πf dove f è la frequenza),
ampiezza massima E e fase iniziale ϕ ,
e(t ) = E cos(ωt +ϕ ) .
(91)
In questo caso bisogna risolvere l’equazione
RC
dv2
+ v2 = E cos(ωt + ϕ ).
dt
(92)
Essendo l’equazione (92) lineare, il termine noto sinusoidale e i suoi
coefficienti costanti nel tempo, è presumibile che essa abbia una soluzione
sinusoidale nel tempo con la stessa pulsazione del termine noto,
v p (t ) = V cos(ωt + α) .
(93)
L’ampiezza massima V e la fase iniziale α sono incognite e devono essere
determinate imponendo che la (93) verifichi l’equazione (92). Sostituendo la
(93) nella (92) si ottiene l’equazione trigonometrica
−ωRCV sin(ωt + α) + V cos(ωt + α) = E cos(ωt + ϕ ) .
(94)
La funzione (91) è soluzione dell’equazione (92) se esistono dei valori di V e
α per i quali l’equazione (94) è verificata per ogni t .
G. Miano, Introduzione ai Circuiti
139
Questi valori esistono e possono essere determinati nel seguente modo. Siccome
le incognite sono due, V e α , basta imporre che la (94) sia verificata in due
istanti di tempo diversi, t1 e t2 , che non differiscano per un multiplo intero del
periodo T = 2π /ω . Conviene scegliere gli istanti t1 e t2 in modo tale che
ωt1 + α = 0,
(95)
ωt2 + α = π / 2 .
(96)
e
Così facendo si ottiene il sistema di equazioni trigonometriche
V = E cos(ϕ − α ) ,
ωRCV = E sin (ϕ − α) .
(97)
(98)
Dalle (97) e (98) si ha immediatamente
V=
E
(99)
,
(ωτ ) +1
α = ϕ − arctg (ωτ ) ,
2
(100)
dove τ è la costante di tempo data dall’espressione (57).
Esercizio
Si dimostri che l’equazione (94) è verificata in ogni istante di tempo se V e α
sono dati dalle espressioni (99) e (100), rispettivamente.
♦
La funzione
v p (t ) =
E
(ωτ)2 +1
cos[ωt + ϕ − arctg (ωτ)]
(101)
G. Miano, Introduzione ai Circuiti
140
è la soluzione sinusoidale del circuito. Allora, la soluzione generale
dell’equazione (92) è
v2 (t) = Aexp (−t / τ) +
E
cos[ωt + ϕ − arctg (ωτ )].
(ωτ)2 +1
(102)
L’espressione (102) rappresenta, al variare della costante di integrazione A
tutte le possibili soluzioni del circuito in esame quando la tensione impressa è
sinusoidale. Imponendo la condizione iniziale (37), in questo caso si ottiene
A = V0 − V cosα .
(103)
La soluzione effettiva del circuito è
v2 (t) = (V0 − V cosα)e −t τ +
E
(ωτ ) +1
2
cos[ωt + ϕ − arctg (ωτ)] .
(104)
Questa è la soluzione del circuito nel caso di generatore sinusoidale. Qualunque
sia la condizione iniziale si ha che
v2 (t) →
0,8
E
(ωτ)2 + 1
cos[ωt + ϕ − arctg(ωτ)] per t → ∞ .
(105)
v 2 [V]
0,6
0,4
0,2
0
-0,2
-0,4
-0,6
5τ
t (s )
-0,8
0
Fig. 2.12
0,005
0,01
0,015
0,02
Evoluzione forzata della tensione del condensatore nel caso per un generatore
sinusoidale.
G. Miano, Introduzione ai Circuiti
141
Il primo termine dell’espressione (104), che è il termine transitorio, tende
esponenzialmente a zero, qualunque sia il valore iniziale della tensione, con la
costante di tempo τ . Dopo che il termine transitorio si è estinto, la soluzione
del circuito è sinusoidale nel tempo con la stessa pulsazione del generatore. Per
tale ragione alla soluzione particolare (101) si dà il nome di soluzione di regime
sinusoidale. Anche in questo caso il termine transitorio dipende dalla
condizione iniziale, mentre quello di regime non dipendente dalla condizione
iniziale.
Si osservi che anche in questo caso il termine transitorio dipende dalla
condizione iniziale, mentre quello di regime non dipende dalla condizione
iniziale.
La soluzione del circuito in evoluzione forzata è
v2 (t) = −E cosαe −t τ +
E
(ωτ)2 +1
cos[ωt + ϕ − arctg (ωτ )] .
(106)
In Figura 2.12 viene riportato il grafico della tensione v2 (t) in evoluzione
forzata (in funzione del tempo), per E = 1V , ω = 103 rad /s , ϕ = 0 , R = 1Ω e
L = 1 mF ; la costante di tempo è τ = 1ms , l’ampiezza massima e la fase iniziale
della soluzione sinusoidale di regime sono V =1/ 2 V ≅ 0,707 V e ϕ = π / 4 . Il
periodo del regime sinusoidale è T = 2π /ω ≅ 6.28 ms.
♦
Esercizio
Si verifichi che l’espressione dell’intensità della corrente elettrica i che
attraversa l’induttore del circuito di Figura 2.7b è
i(t) = ( I0 − I cosα)e −t τ +
E
1
cos[ωt + ϕ − arctg (ωτ )] ,
R (ωτ)2 +1
(107)
dove la costante di tempo τ è data dalla relazione (66) e I0 è il valore iniziale
dell’intensità della corrente elettrica che attraversa l’induttore. La soluzione in
evoluzione forzata è
G. Miano, Introduzione ai Circuiti
142
i(t) = −I cosαe−t τ +
E
1
cos[ωt + ϕ − arctg(ωτ)] .
R (ωτ)2 +1
(108)
♦
Esercizio
Si determini la tensione del condensatore per il circuito di Figura 2.7a in
evoluzione forzata quando la tensione impressa dal generatore è
e(t ) = E 0 + E1 cos(ωt ) ; si assuma: E0 = E1 = 1V , ω = 103 rad /s , R = 1Ω e
C = 1 mF .
♦
Esercizio
In Figura 2.13 sono illustrati due circuiti del primo ordine alimentati da un
generatore di corrente. In entrambi i circuiti i bipoli sono collegati in parallelo.
Due bipoli sono connessi in parallelo, se i loro terminali sono connessi alla
stessa coppia di nodi. Si determini: a) l’evoluzione forzata del circuito RC
illustrato in Figura 2.13a per j(t ) = J 0 = 1 A, R = 1Ω e C = 0,5 mF ; b)
l’evoluzione forzata del circuito RL illustrato in Figura 2.13b per
j(t ) = J sinωt , J = 1 A, ω = 103 rad /s , R = 1Ω e L = 1 mH . Infine, si
determinino le potenze istantanee erogate dai due generatori di corrente.
j(t)
R
C
j(t)
(a)
Fig. 2.13
R
L
(b)
Esempi di circuiti dinamici del primo ordine.
♦
2.5 Circuito dinamico non lineare del primo ordine
Si consideri, ora, il circuito illustrato in Figura 2.14. Il generatore di tensione
è stazionario, il condensatore è lineare e tempo invariante, un resistore è lineare
G. Miano, Introduzione ai Circuiti
143
e l’altro è non lineare. Analizzeremo le dinamiche di questo circuito facendo
riferimento alle due curve caratteristiche che abbiamo già considerato,
precedentemente, nello studio del circuito resistivo non lineare riportato in
Figura 2.3.
Il circuito di Figura 2.14 può essere ottenuto da quello di Figura 2.3 collegando
in parallelo al resistore non lineare un condensatore di capacità C . Due bipoli
sono connessi in parallelo, se i loro terminali sono connessi alla stessa coppia di
nodi. Il condensatore potrebbe essere anche il modello di effetti capacitivi
parassiti esistenti all’interno del resistore non lineare (ad, esempio, la capacità
di giunzione di un diodo).
Il resistore non lineare è collegato in parallelo al condensatore, e quindi, le loro
tensioni sono uguali. Questo risultato è immediato e lo si ottiene applicando la
legge di Kirchhoff per le tensioni alla maglia costituita dal resistore non lineare
e dal condensatore. Per questa ragione nel disegno riportato in Figura 2.14a è
indicata solo la tensione v .
La tensione del condensatore v è la grandezza di stato del circuito. In questo
circuito il resistore non lineare non è in serie con il resistore lineare a causa
della presenza del condensatore in parallelo.
+
+
v1
i1 “1”
i2
R1
i2
i3 +
v
E
C
−
(a)
Fig. 2.14
i2
“2”
−
v
(b)
v
(c)
(a) Circuito dinamico non lineare; curve caratteristiche tipiche di resistori non
lineari: (b) diodo a giunzione pn, (c) diodo tunnel.
Determiniamo, ora, le equazioni circuitali. Applicando la legge di Kirchhoff
per le correnti al nodo “1” abbiamo
i1 − i2 − i3 = 0 .
(109)
Applicando, ora, la legge di Kirchhoff per la tensione alla maglia definita dal
generatore di tensione, dal resistore lineare e dal resistore non lineare (o dal
condensatore) abbiamo l’equazione
G. Miano, Introduzione ai Circuiti
144
v + v1 − E = 0.
(110)
Dalle relazioni caratteristiche del resistore lineare, del resistore non lineare e del
condensatore abbiamo le equazioni
v1 − R1i1 = 0,
i2 − g(v ) = 0,
dv
i3 − C = 0 .
dt
(111)
(112)
(113)
All’equazione differenziale (113) bisogna affiancare, per una descrizione
completa del condensatore, e quindi del circuito, il valore della tensione del
condensatore all’istante iniziale,
v(t = 0 ) = V0 .
(114)
L’insieme delle equazioni (109)-(113) sono un sistema di 5 equazioni nelle
altrettante incognite i1 , i2 , i3 , v1 e v . È evidente che le difficoltà nella
soluzione di questo problema sono superiori alle difficoltà che abbiamo
incontrato sia nello studio del circuito resistivo non lineare, sia nello studio del
circuito dinamico lineare, perché bisogna risolvere, come tra poco faremo
vedere, un’equazione differenziale non lineare.
Anche in questo caso è opportuno ridurre l’intero sistema di equazioni ad una
sola equazione differenziale in una sola incognita, e conviene scegliere come
incognita la tensione del condensatore. Questa è anche la grandezza che appare
sotto l’operazione di derivata nell’unica equazione differenziale (equazione
(113)) del sistema di equazioni del circuito.
Sostituendo l’espressione di v1 data dall’equazione (110) nell’equazione (111)
si ha
i1 =
E−v
.
R1
(115)
Ora, sostituendo nell’equazione (109) l’espressione di i1 data dalla (115),
l’espressione di i2 data dalla (112) e l’espressione di i3 data dalla (113), si
ottiene l’equazione cercata
G. Miano, Introduzione ai Circuiti
145
C
dv v
E
+ + g(v ) = .
dt R
R
(116)
Questa è un’equazione differenziale del primo ordine, non lineare e con termine
noto costante. Anche essa ha infinite soluzioni. Per determinarne una sola,
quella che si realizza nel circuito, bisogna imporre che la soluzione verifichi
anche la condizione iniziale (114). Una volta determinata la tensione del
condensatore, utilizzando le equazioni algebriche (109)-(112) possiamo
determinare tutte le altre grandezze del circuito.
Anche se in questo caso particolare l’equazione (116) potrebbe essere risolta
analiticamente attraverso la tecnica della separazione delle variabili (lasciamo al
lettore volenteroso la sua soluzione), nella maggior parte dei casi ciò non è
possibile. E’ necessario ricorrere, in generale, a metodi approssimati di tipo
numerico per la soluzione di equazioni differenziali non lineari.
Questo corso introduttivo alla teoria dei circuiti tratta, sostanzialmente, di
circuiti lineari. L’insegnamento di metodi di soluzione di equazioni
differenziali non lineari attraverso metodi numerici esula dagli obiettivi del
corso. Noi, qui, ci limiteremo solo a descrivere le proprietà qualitative più
importanti delle soluzioni dell’equazione (116) utilizzando di nuovo un metodo
“grafico”. Riscriviamo l’equazione (116) nel modo seguente
C
dv E − v
− g(v) .
=
dt R
y
y
G
G
R
R
I1
I2
I3
I
V0 V V0
(a)
Fig. 2.15
(117)
v
V0 V1 V2
V3 V0
v
(b)
Discussione grafica del comportamento della soluzione del circuito di Figura
2.9 per i due casi in esame.
G. Miano, Introduzione ai Circuiti
146
Si riporti sul piano (v, y) , Figura 2.15, la curva caratteristica G del resistore
non lineare definita dall’equazione
yG = g(v) .
(118)
Poi sullo stesso piano si riporti la retta R definita dall’equazione
yR =
E −v
.
R
(119)
Allora, l’equazione differenziale (117) può essere scritta come
C
dv
= y R (v) − yG (v) .
dt
(120)
In corrispondenza dei punti di intersezione tra la retta R e la curva G si ha che
y R (V ) = yG (V ) ,
(121)
e quindi
C
dv
dt
v=V
= y R (V ) − yG (V ) = 0 .
(122)
Dunque, i valori di tensione V corrispondenti ai punti di intersezione tra la
retta R e la curva G sono le soluzioni stazionarie del circuito 8 .
In condizioni stazionarie il condensatore si comporta come se fosse un circuito
aperto, perché essendo la tensione costante nel tempo l’intensità della corrente
elettrica che lo attraversa è nulla. Di conseguenza in condizioni stazionarie le
soluzioni del circuito in esame coincidono con quelle del circuito resistivo non
lineare analizzato nel paragrafo 2.3 e rappresentato in Figura 2.3.
In accordo a quanto già visto nel paragrafo 2.3, il circuito in esame ha una sola
soluzione stazionaria se la curva caratteristica del resistore non lineare è
8 A partire dalla (116) si può dimostrare che, oltre a dv / dt
v =V
= 0 , si ha anche
d 2 v /dt 2 v =V = 0, d 3 v / dt 3 v =V = 0, e così via. Ciò implica che v = V è una soluzione
stazionaria del circuito.
G. Miano, Introduzione ai Circuiti
147
monotona crescente, Figura 2.15a. Invece, se la curva caratteristica è non
monotona le soluzioni stazionarie possono essere più di una, Figura 2.15b.
Se il valore iniziale della tensione del condensatore è uguale al valore
stazionario, V0 = V , il circuito si trova fin dall’istante iniziale in regime
stazionario. Cosa accade se V0 ≠ V ?
Quando v ≠ V si ha dv / dt ≠ 0 e la soluzione del circuito non è stazionaria, ma
varia nel tempo. Il comportamento dinamico del circuito dipende dal segno del
dv / dt .
Analizziamo, prima, il caso in cui la curva caratteristica del resistore non
lineare è monotona crescente, Figura 2.15a. A sinistra della retta (verticale)
v = V il punto appartenente alla retta R corrispondente a un dato valore di
tensione v (v < V ) è sempre al di sopra del corrispondente punto appartenente
alla curva G , mentre a destra della retta v = V , cioè per v > V , accade il
contrario. Quando il punto di R corrispondente al valore di tensione v è al di
sopra del corrispondente punto di G , si ha y R (v ) − y G (v ) > 0 e quindi dv / dt > 0
perché C > 0. Invece, quando il punto di R corrispondente al valore di
tensione v è al di sotto del corrispondente punto di G , si ha y R (v ) − y G (v ) < 0
e quindi dv / dt < 0 ( C > 0). I risultati che abbiamo appena ottenuto sono
riassunti dalla relazione
> 0
dv
= 0
dt
< 0
v > V,
v = V,
v < V.
(123)
Da queste considerazioni si ha che, se il valore iniziale della tensione, V0 , è
maggiore di V , la tensione v(t ) decresce fino a quando non raggiunge il valore
stazionario V , invece se V0 è minore di V , v(t ) cresce fino a quando non
raggiunge il valore stazionario V , Figura 2.15a. Infine, se V0 = V si ha
v(t ) = V . Comunque siano le condizioni iniziali, la soluzione tende
asintoticamente alla soluzione v = V , che è l’unica soluzione stazionaria del
circuito.
In questo caso si dice che la soluzione stazionaria v = V è stabile: comunque si
scelga un intorno di v = V e per ogni condizione iniziale appartenente a tale
intorno, il circuito evolve in modo tale da raggiungere l’unico regime
stazionario v = V . In questo caso si dice anche che il regime stazionario v = V è
l’attrattore di tutte le soluzioni del circuito.
G. Miano, Introduzione ai Circuiti
148
Si consideri, ora, il caso in cui la caratteristica G è non monotona (Figura
2.15b), e interseca la retta R in tre punti. I valori di tensione corrispondenti a
questi tre punti, V1 , V2 , V3 , sono le soluzioni stazionarie del circuito. (Se la
retta R intersecasse la curva G in un solo punto la dinamica avrebbe le stesse
caratteristiche che sono state descritte nel caso precedente.)
I punti di R corrispondenti a valori di v inferiori a V1 sono sempre al di sopra
dei corrispondenti punti di G ; pertanto si ha y R (v ) − y G (v ) > 0 per v < V1 .
I punti di R corrispondenti a valori di v compresi tra le due soluzioni
stazionarie v = V1 e v = V2 sono sempre al di sotto dei corrispondenti punti di
G , quindi y R (v ) − y G (v ) < 0 per V1 < v < V2 .
I punti di R corrispondenti a valori di v compresi tra le due soluzioni
stazionarie v = V2 e v = V3 sono sempre al di sopra dei corrispondenti punti di
G , quindi y R (v ) − y G (v ) > 0 per V2 < v < V3 .
Infine, i punti di R corrispondenti a valori di v superiori a V3 sono sempre al
di sotto dei corrispondenti punti di G , quindi y R (v ) − y G (v ) < 0 per V3 < v .
Essendo C > 0, si ha allora
> 0
dv
= 0
dt
< 0
Condizione iniziale
V0 < V1
V0 = V1
V1 < V0 < V2
V0 = V2
V2 < V0 < V3
V0 = V3
V0 > V3
Tab. 2.3
v < V1 o V2 < v < V3 ,
v = V1 o v = V2 o v = V3 ,
V1 < v < V2 o v < V3 .
Segno di dv / dt
dv / dt > 0
dv / dt = 0
dv / dt < 0
dv / dt = 0
dv / dt > 0
dv / dt = 0
dv / dt < 0
(124)
Comportamento di v(t ) per t → ∞
v(t ) → V1
v(t ) = V1
v(t ) → V1
v(t ) = V2
v(t ) → V3
v(t ) = V3
v(t ) → V3
Riassunto del comportamento asintotico della tensione del condensatore nel
caso riportato in Figura 2.15b.
In questo caso il regime stazionario che il circuito raggiunge dipende dalla
condizione iniziale del condensatore. I possibili comportamenti asintotici della
tensione del condensatore (cioè i comportamenti per t → ∞ ) sono riportati in
Figura 2.15b e riassunti in Tabella 2.3. Le due soluzioni stazionarie v(t ) = V1 e
G. Miano, Introduzione ai Circuiti
149
v(t ) = V3 sono soluzioni stazionarie stabili, mentre la soluzione stazionaria
v(t ) = V2 è instabile: comunque si scelga il valore della condizione iniziale V0
prossimo al valore della soluzione stazionaria V2 il circuito evolve sempre in
maniera tale da raggiungere la soluzione stazionaria v(t ) = V1 o la soluzione
stazionaria v(t ) = V3 , cioè tende sempre ad allontanarsi dalla soluzione
stazionaria v(t ) = V2 . Le soluzioni stazionarie v(t ) = V1 e v(t ) = V3 sono gli
attrattori delle soluzioni del circuito: quale di questi due viene raggiunto
dipende solo dalla condizione iniziale. Attraverso circuiti di questo tipo è
possibile realizzare circuiti bistabili e memorie binarie.
2.6
Grafo di un circuito
Dal modo stesso in cui sono state enunciate le leggi di Kirchhoff, discende che
esse non fanno alcun riferimento alla struttura “interna” dei diversi componenti.
Le equazioni che si ottengono imponendo le leggi di Kirchhoff, equazioni di
Kirchhoff, dipendono solo da come gli elementi circuitali sono connessi tra loro
e non dalla loro natura fisica.
5
“1”
1 −
“2”
4
6
3
“4”
“3”
2
5
“1”
“2”
6
1
4
3
“4”
(a)
“3”
2
(b)
Fig. 2.16 Due circuiti con lo stesso grafo.
Si considerino i due esempi di circuito, riportati in Figura 2.16. Benché siano
costituiti da bipoli diversi, essi hanno due cose in comune:
(i) il numero di nodi e di bipoli;
(ii) il modo in cui i bipoli sono tra loro collegati.
G. Miano, Introduzione ai Circuiti
150
Nei due circuiti i valori delle grandezze incognite sono, ovviamente, diverse,
ma le relazioni tra di esse che si ottengono applicando le leggi di Kirchhoff
sono le stesse. In conseguenza di ciò le equazioni di Kirchhoff per le intensità
di corrente e le tensioni del circuito illustrato in Figura 2.16a sono uguali alle
equazioni di Kirchhoff per le intensità di corrente e le tensioni del circuito
illustrato in Figura 2.16b.
Da questa semplice constatazione deriva che, per scrivere le equazioni di
Kirchhoff di un determinato circuito non occorre fare riferimento
specificamente al sistema fisico che lo costituisce, ma è sufficiente riferirsi a
una struttura astratta di tipo “geometrico” (in realtà non occorre neppure questa
caratteristica) che contenga soltanto:
(a) i nodi (tutti) del circuito;
(b) i collegamenti tra questi realizzati tramite i bipoli.
Alle equazioni di Kirchhoff ci si riferisce a volte usando l’espressione
“equazioni topologiche” per evidenziare il fatto che esse dipendono solo dalle
caratteristiche topologiche del circuito.
“1”
“2”
5
“1”
1
6
“2” “1”
“3”
“4”
(a)
“2”
5
3 4
2
2
Fig. 2.17
5
“4”
“3” “4”
(b)
“1”
1
6
“2”
3 4
2
2
“3”
(c)
5
“4”
“3”
(d)
(a) Circuito; (b) grafo corrispondente; (c) circuito orientato; (d) grafo orientato
corrispondente.
Si consideri il circuito di bipoli disegnata in Figura 2.17a e il corrispondente
schema “geometrico” di Figura 2.17b. Questo schema è un esempio di grafo 9 .
Come si vede, nel grafo, i bipoli sono “scomparsi”, mentre tutti i nodi sono
presenti: al posto dei bipoli, sono stati semplicemente indicati delle linee detti
9 Eulero scrisse il primo lavoro sulla teoria dei grafi nel 1736; in questo lavoro Eulero trattò il
problema del ponte di Königsberg. Nel 1847 Kirchhoff ha fondato la teoria dei grafi, così
come è nota oggi, nei suoi studi sui circuiti elettrici. La maggior parte delle proprietà
topologiche dei circuiti elettrici sono state trovate da Kirchhoff e da Maxwell (1892).
L’applicazione sistematica dei grafi allo studio dei circuiti elettrici è più recente (1957).
G. Miano, Introduzione ai Circuiti
151
“lati”, che collegano fra loro i nodi allo stesso modo che nel circuito di
partenza. I due circuiti riportati in Figura 2.16 hanno lo stesso grafo.
Ora, è immediato constatare che, se i bipoli di Figura 2.17a vengono orientati
in base ai versi di riferimento delle intensità di corrente, scelti in modo
qualsiasi (come, ad esempio, in Figura 2.17c), e, allo stesso tempo, lo schema
corrispondente è orientato, lato per lato, allo stesso modo (Figura 2.17d), per
scrivere le equazioni di Kirchhoff per le correnti è sufficiente riferirsi al grafo
orientato, piuttosto che al circuito di partenza.
È, inoltre, evidente che, anche la scrittura delle equazioni esprimenti le leggi di
Kirchhoff per le tensioni può essere effettuata basandosi esclusivamente sul
grafo orientato (senza bisogno di ricorrere al circuito di partenza). La cosa è di
per sé ovvia quando si stabilisca, una volte per tutte, di fare per ogni bipolo del
circuito, ad esempio, la convenzione dell’utilizzatore. Quando si fa questa
scelta, non occorre orientare ulteriormente il grafo (per le tensioni): è
sufficiente averlo orientato per le intensità di corrente.
Si noti che, se in luogo del grafo di Figura 2.17b se ne sceglie un altro che
differisca dal primo per il fatto che ciascuno dei lati sia stato deformato ad
arbitrio (purché senza “lacerazione”), le equazioni di Kirchhoff per le correnti e
per le tensioni conservano ancora la stessa forma. Per questo motivo, si è soliti
dire che il grafo di una rete non ha significato geometrico (il che implicherebbe
la conservazione di distanze e angoli rispetto al circuito di partenza), bensì
soltanto significato “topologico” (il che implica soltanto la conservazione dei
collegamenti fra i diversi nodi).
In conclusione, il modo in cui i bipoli di un circuito sono collegati tra loro può
essere rappresentato tramite un oggetto astratto: il grafo del circuito. Questo
oggetto è “formato” dall’insieme dei nodi e dei lati del circuito e dalla
relazione, detta relazione di incidenza, che a ogni lato fa corrispondere la
coppia di nodi nei quali quel lato (bipolo) incide. Di solito, il grafo è
rappresentato graficamente attraverso elementi geometrici: il nodo è
rappresentato da un punto e il lato da un arco di linea.
2.7
Elementi di topologia dei circuiti: albero, coalbero, maglia, anello
Per studiare le proprietà dei circuiti che dipendono solo dalle caratteristiche
delle connessioni c’è bisogno di alcuni elementi di base della teoria dei grafi.
Nel riportarli useremo dei termini che è importante definire subito.
G. Miano, Introduzione ai Circuiti
152
Definizioni: grafo, grafo orientato, sottografo
•
Un grafo G(N,L) è costituito dall’insieme di n nodi, che indicheremo con
N = {“1”,“2”,...,“n”} , dall’insieme di l lati (bipoli), che indicheremo con
L = {1, 2,...,l} , e dalla relazione di incidenza che a ogni lato (bipolo) fa
corrispondere la coppia di nodi nei quali quel lato incide. Per convenzione,
ciascun lato del grafo di un circuito è orientato con la freccia che indica il
verso di riferimento dell’intensità della corrente che attraversa il
corrispondente bipolo.
•
Se ogni lato (bipolo) del grafo è orientato il grafo si dice orientato.
•
Si consideri un grafo G(N,L) . Il grafo G1(N,L) si dice sottografo di
G(N,L) , se N 1 è un sottoinsieme di N , L1 è sottoinsieme di L e la
relazione di incidenza tra i nodi di N 1 e i lati di L1 è la stessa relazione
che si ha nel grafo G(N,L) .
♦
In Figura 2.18a è illustrato un grafo non orientato, e in Figura 2.18b è illustrato
lo stesso grafo ma orientato. In Figura 2.19 un grafo orientato, insieme con tre
sottografi, è illustrato. Un sottografo è una parte di un grafo, e quindi
corrisponde a una parte del circuito.
“1”
6
“6”
5
1
2
8
6
7
“7” 3 “6”
4
9
“5”
5
“4”
(a)
Fig. 2.18
“3” “1”
“2”
“2”
1
“3”
2
8
7
“7” 3
4
9
“5”
“4”
(b)
(a) un grafo G(N,L) : N = {“1”,“2”, ...,“6”} , L = {1,2,...,9} ; (b) una possibile
orientazione del grafo G(N,L) .
Un concetto fondamentale nella teoria dei grafi è quello di grafo connesso.
G. Miano, Introduzione ai Circuiti
153
Definizione: grafo connesso
Un grafo si dice connesso se ogni nodo è collegato a qualsiasi altro nodo
attraverso uno o più lati.
♦
In Figura 2.20a è illustrato un grafo connesso e in Figura 2.20b è illustrato un
esempio di grafo non connesso: ad esempio, il nodo “1” non è collegato al nodo
“5”.
“1”
4
“4” “1”
5
1
“2”
Fig. 2.19
“1”
1
“2”
Fig. 2.20
4
“4”
5
3
“3”
2
G
3 1
“3”
4
“4” “1”
“1”
3
“2”
2
G2
G1
“3” “2”
“3”
2
G3
Grafo e alcuni suoi sottografi (orientati).
4
“4”
5
2
(a)
3
“3”
“1”
4
“4” “5”
1
“2”
3
“3”
(b)
2
5
“6”
7
6
“7”
(a) grafo connesso; (b) grafo non connesso.
I circuiti di bipoli di interesse nelle applicazioni sono tutti connessi, e quindi
considereremo solo grafi connessi. Un grafo connesso può contenere sottografi
non connessi (si consideri, ad esempio, il grafo G illustrato in Figura 2.19 e il
sottografo G3 ). Circuiti di interesse con grafi non connessi sono i circuiti che
G. Miano, Introduzione ai Circuiti
154
contengono elementi con più di due terminali, come, ad esempio, doppi bipoli.
Analizzeremo nel Capitolo 4 queste situazioni.
Il concetto di maglia, che è stato introdotto nel precedente capitolo, quando
abbiamo formulato la legge di Kirchhoff per le tensioni, è anche un concetto
fondamentale della teoria dei grafi.
Definizione: maglia
Sia dato un grafo connesso G . Una maglia di G è un sottografo connesso
in cui in ciascun nodo incidono due e solo due lati.
♦
“1”
4
5
1
“2”
2
G
Fig. 2.21
31
“4” “1”
4
2
M1
“4” “1”
5
3
“3” “2”
5
31
“3”
“3” “2”
M2
2
M3
“3”
Le maglie del grafo G .
“1”
4
“4”
5
1
“2”
Fig. 2.22
4
“4” “1”
2
G
“1”
4
“4” “1”
3 1
“3”
“2”
1
2
G4
4
“4”
5
“3”
3
“3”
G5
Esempi di sottografi di G che non sono maglie di G .
Ogni maglia forma un percorso chiuso, perché essa deve essere un sottografo
connesso in cui in ogni nodo incidono due e due soli lati: percorrendo la maglia
ciascun lato e ciascun nodo vengono incontrati una e una sola volta. Questa è la
proprietà fondamentale di ogni maglia. Una maglia orientata è una maglia a cui
è associata un verso di percorrenza.
G. Miano, Introduzione ai Circuiti
155
In generale, in un grafo ci sono più maglie. In Figura 2.21 sono riportate tutte
le possibili maglie del grafo G di Figura 2.19. I sottografi G4 e G5 dello stesso
grafo G , riportati in Figura 2.22, non sono maglie perché nei nodi “3” e “4” di
G4 incide solo un lato e nel nodo “1” di G5 incidono tre lati.
Oltre alle maglie, ci sono altri sottografi che hanno proprietà interessanti e che
saranno utilizzati nella teoria dei circuiti: essi sono gli alberi e i coalberi di un
grafo.
Definizioni: albero, coalbero
•
•
Sia dato un grafo connesso G . Un albero A di G è un suo sottografo
connesso costituito da tutti i nodi del grafo e che non contiene maglie.
Il coalbero CA di G , corrispondente all’albero A , è l’insieme dei lati
complementare a quelli dell’albero: l’unione dei lati dell’albero e del
coalbero coincide con l’insieme di tutti i lati di G .
♦
“1”
4
“4”
5
1
“2”
2
G
4
“1”
3 1
“3”
“2”
1
2
A1
5
CA1
Fig. 2.23
“4” “1”
4
“4”
5
“3”
“3”
A2
3
3
2
CA2
Esempi di alberi, A1 , A2 , e coalberi, CA1 , CA2 , del grafo G .
In generale un grafo possiede più di un albero. Due alberi, A1 , A2 e i relativi
coalberi, CA1 , CA 2 del grafo G riportato in Figura 2.19, sono illustrati in Figura
2.23. Il sottografo G3 del grafo G riportato in Figura 2.24 non è un albero
G. Miano, Introduzione ai Circuiti
156
perché contiene una maglia, e così, anche il sottografo G4 non è un albero
perché non è connesso.
“1”
1
“2”
Fig. 2.24
4
“4”
5
2
G
“1”
3 1
“3”
“2”
4
“4” “1”
4
“4”
“3” “2”
2
G4
“3”
5
2
G3
Esempi di sottografi di G che non sono alberi di G .
Proprietà fondamentale degli alberi di un grafo connesso
Si consideri un grafo connesso G con n nodi e l lati. Ciascun albero del grafo
G è costituito da (n −1) lati (indipendentemente dal numero di lati del grafo e
dalla relazione di incidenza).
♦
La dimostrazione di questa proprietà è semplice. Si parta da un qualsiasi nodo
dell’albero. È possibile raggiungere, percorrendo l’albero, qualsiasi altro nodo.
Ogni volta che si raggiunge un altro nodo si percorre un nuovo lato; pertanto il
numero totale di lati distinti che bisogna percorrere per raggiungere tutti i nodi
è (n −1) , cioè è uguale al numero di nodi meno uno (quello di partenza).
Da questa proprietà segue anche che, per ogni grafo connesso con n nodi e l
lati (bipoli) deve essere necessariamente l > (n −1).
Proprietà fondamentale del coalbero di un grafo connesso
Si consideri un grafo connesso G con n nodi e l lati. Ciascun coalbero del
grafo G è costituiti da [l − (n − 1)] lati (indipendentemente dalla relazione di
incidenza del grafo).
♦
G. Miano, Introduzione ai Circuiti
157
Questa proprietà deriva direttamente dal fatto che il coalbero è il complemento
all’albero, cioè la somma dei lati dell’albero e del coalbero deve essere uguale
al numero dei lati del grafo.
Tra tutte le possibili maglie di un grafo c’è ne sono alcune che hanno una
proprietà molto interessante: attraverso queste maglie, che ora individueremo, è
possibile rappresentare tutte le possibili maglie del grafo.
Si consideri un grafo connesso G con n nodi e l lati. Si scelga un albero A .
Per ciascun lato del coalbero CA (corrispondente all’albero scelto) esiste una e
una sola maglia costituita dal suddetto lato di coalbero e da rami dell’albero.
“1”
4
“4”
5
1
“2”
2
G
“3”
“2”
3
“2”
2
CA
A
4
“1”
5
1
“4”
5
3 1
“1”
Fig. 2.25
4
“1”
2
MF1
“4”
5
“3”
MF2
3
“3”
“1”
1
“2”
“4”
5
2
M
3
“3”
Grafo G , un albero A e corrispondente coalbero CA ; l’insieme delle maglie
fondamentali del coalbero CA ; la maglia M è “unione” delle maglie
fondamentali MF1 e MF2 .
Definizione: maglia fondamentale
• Si consideri il sottografo che si ottiene aggiungendo all’albero A un solo
lato del coalbero CA : esso contiene una e una sola maglia, che si ottiene
eliminando tutti i lati “appesi”, cioè tutti quei lati che non appartengono al
G. Miano, Introduzione ai Circuiti
158
percorso chiuso. Una maglia ottenuta in questo modo prende il nome di
maglia fondamentale del coalbero CA .
♦
È evidente, allora, che aggiungendo un lato di coalbero per volta è possibile
costruire [l − (n − 1)] maglie fondamentali distinte. Questo insieme di maglie
prende il nome di insieme delle maglie fondamentali del coalbero CA del grafo
G . A ciascun coalbero corrisponde un diverso insieme di maglie fondamentali.
La proprietà dell’insieme delle maglie fondamentali di un coalbero è che ogni
lato di coalbero appartiene a una e una sola maglia fondamentale dell’insieme e,
quindi, ogni maglia dell’insieme delle maglie fondamentali ha almeno un lato
in esclusiva. In questo senso possiamo allora dire che l’insieme delle maglie
fondamentali di un coalbero sono tra loro indipendenti.
Si consideri ora l’insieme di maglie fondamentali di un coalbero del grafo G .
Si può verificare che una qualsiasi altra maglia del grafo può essere
rappresentata tramite “l’unione” di maglie fondamentali. La regola dell’unione
deve prevedere che:
(i) le maglie abbiano almeno un lato in comune ;
(ii) i lati in comune si elidano a vicenda.
In Figura 2.25 è illustrato un grafo e un possibile insieme di maglie
fondamentali ( MF1 è la maglia fondamentale ottenuta aggiungendo all’albero
A il lato 2 e MF2 è quella ottenuta aggiungendo il lato 3; la maglia M è
ottenuta “unendo” MF1 a MF2 ).
“1”
6
1
“2”
Fig. 2.26
4
“4”
5
2
G
“1”
5
3 1
“3”
“2”
2
AN 1
Grafo planare e anelli corrispondenti.
G. Miano, Introduzione ai Circuiti
4
“1”
“4”
5
“3”
3 6
“3”
AN 2
“1”
1
“2”
AN 3
159
Tutti i circuiti che vengono considerati in questo corso hanno grafi planari.
Fino ad ora abbiamo considerato solo grafi di questo tipo.
Definizione: grafo planare
• Un grafo si dice planare se può essere tracciato su di un piano senza che
nessuna coppia di lati si intersechi in un punto che non sia un nodo.
♦
In Figura 2.26 è riportato un esempio di grafo planare. In Figura 2.27a è
riportato un esempio di grafo non planare. Se si prova a distendere questo grafo
su di un piano, il lato 1, che collega il nodo “5” al nodo “8”, interseca almeno
un altro lato in un punto diverso dai nodi (Figura 2.27b).
“1”
“4”
“2”
1
“5”
“6”
“1”
“2”
“4”
“3”
“3”
1
“6”
“7”
“8”
(a)
Fig. 2.27
“5”
“7”
“8”
(b)
(a) Esempio di grafo non planare; (b) lo stesso grafo disteso su di un piano.
Per i grafi planari ogni maglia partiziona il piano in due regioni, quella interna
al cammino chiuso e quella esterna. Tra tutte le possibili maglie di un grafo
planare, rivestono particolare interesse quelle che non contengono nessun lato al
loro interno.
Definizione: anello
• Un anello è una maglia di un grafo planare che non contiene lati al suo
interno.
♦
G. Miano, Introduzione ai Circuiti
160
Proprietà fondamentale degli anelli di un grafo planare
Si consideri un grafo planare connesso G con n nodi e l lati. Il grafo G ha
[l − (n − 1)] anelli.
♦
Gli anelli di un grafo planare sono maglie tra loro indipendenti. Qui il concetto
di indipendenza sta a significare che non è possibile ottenere uno qualsiasi degli
[l − (n − 1)] anelli dall’unione, secondo la regola che abbiamo appena enunciato,
degli [l − (n −1)] −1 anelli restanti. Questa nuova accezione del concetto di
indipendenza comprende quello che abbiamo appena introdotto quando
abbiamo considerato l’insieme delle maglie fondamentale di un coalbero. Non
dimostreremo questa proprietà. Può essere facilmente verificata per induzione.
L’insieme di tutti gli anelli di un grafo planare ha la stessa proprietà di un
insieme di maglie fondamentali: qualsiasi altra maglia del grafo planare può
essere ottenuta dall’unione di due o più anelli. In Figura 2.26 sono riportati
tutti gli anelli, AN 1 , AN 2 e AN 2 del grafo planare G .
A differenza dell’insieme di maglie fondamentali, che dipende dalla scelta
dell’albero, l’insieme degli anelli di un grafo planare è unico.
AN 1
(a)
Fig. 2.28
(b)
(a) Gli anelli di questo grafo sono un insieme di maglie fondamentali; (b) gli
anelli di questo grafo non sono un insieme di maglie fondamentali.
Osservazione
G. Miano, Introduzione ai Circuiti
161
In generale, gli anelli di un grafo planare non costituiscono un insieme di
maglie fondamentali. Gli anelli del grafo planare di Figura 2.28a sono anche un
insieme di maglie fondamentali. Il lettore lo dimostri individuando l’albero e,
quindi, il coalbero a cui tale insieme corrisponde. Invece, gli anelli del grafo
planare di Figura 2.28b non sono un insieme di maglie fondamentali. La
ragione è molto semplice: l’anello interno AN 1 non ha nessun lato in esclusiva
pur essendo indipendente da tutti gli altri anelli del grafo.
2.8
Insiemi di taglio
Un altro importante concetto della teoria dei grafi (e quindi della teoria dei
circuiti) è l’insieme di taglio.
Definizione: insieme di taglio
• Si consideri un grafo connesso G(N,L) . Un sottoinsieme T dei lati L del
grafo, si dice insieme di taglio se:
(a) la rimozione dal grafo di tutti i lati dell’insieme di taglio conduce a un
grafo non connesso;
(b) il ripristino di uno qualsiasi dei lati dell’insieme di taglio riconnette i due
sottografi.
Se il grafo è orientato, l’insieme di taglio si dice orientato.
♦
In Figura 2.29 è illustrato un grafo e i possibili insiemi di taglio, T1 , T 2 , T 3 e
T 4 . I lati di T 2 sono tutti quelli che incidono nel nodo “2” e i lati di T 3 sono
tutti quelli che incidono nel nodo “3”; invece i lati degli insiemi T1 e T 4 non
incidono in uno stesso nodo.
Ciascun insieme di taglio crea una partizione dell’insieme dei nodi N del grafo
G(N,L) in due sotto insiemi, uno che denomineremo sottoinsieme N + e l’altro
che denomineremo sottoinsieme N − . Di conseguenza, ciascun insieme di taglio
può essere orientato scegliendo arbitrariamente un verso, ad esempio, quello
che va dal sottoinsieme di nodi N + al sottoinsieme N − .
G. Miano, Introduzione ai Circuiti
162
La legge di Kirchhoff per le correnti, per come è stata formulata, impone un
legame alle intensità di corrente dei bipoli (lati) che incidono in uno stesso
nodo. È possibile formularla anche per le intensità di corrente dei bipoli (lati)
di un insieme di taglio che, in generale, non incidono in uno stesso nodo.
Equazioni di Kirchhoff per gli insiemi di taglio
La somma algebrica delle intensità di corrente dei bipoli che formano un
insieme di taglio è uguale a zero in ogni istante.
“1”
1
“2”
4
4
“4”
5
5
3
2
G
“3”
4
1
2
T1
5
1
2
T3
T2
4
5
3
T4
Fig. 2.29
2
T5
3 1
5
3
T6
Possibili insiemi di taglio del grafo G .
In Figura 2.29 è illustrato un grafo e i possibili insiemi di taglio, T1 , T 2 , T 3 e
T 4 . I lati di T 2 sono tutti quelli che incidono nel nodo “2” e i lati di T 3 sono
tutti quelli che incidono nel nodo “3”; invece i lati degli insiemi T1 e T 4 non
incidono in uno stesso nodo.
Ciascun insieme di taglio crea una partizione dell’insieme dei nodi N del grafo
G(N,L) in due sotto insiemi, uno che denomineremo sottoinsieme N + e l’altro
che denomineremo sottoinsieme N − . Di conseguenza, ciascun insieme di taglio
G. Miano, Introduzione ai Circuiti
163
può essere orientato scegliendo arbitrariamente un verso, ad esempio, quello
che va dal sottoinsieme di nodi N + al sottoinsieme N − .
La legge di Kirchhoff per le correnti, per come è stata formulata, impone un
legame alle intensità di corrente dei bipoli (lati) che incidono in uno stesso
nodo. È possibile formularla anche per le intensità di corrente dei bipoli (lati)
di un insieme di taglio che, in generale, non incidono in uno stesso nodo.
Equazioni di Kirchhoff per gli insiemi di taglio
La somma algebrica delle intensità di corrente dei bipoli che formano un
insieme di taglio è uguale a zero in ogni istante.
♦
Nella legge per l’insieme di taglio intervengono con lo stesso segno le intensità
di corrente il cui riferimento per il verso è concorde con l’orientazione
dell’insieme di taglio e con il segno contrario le intensità di corrente con
riferimento opposto. Ad esempio, l’intensità di corrente i k deve essere sommata
con il segno + se il suo verso di riferimento per va dal sottoinsieme di nodi N +
al sottoinsieme N − e con il segno − nel caso contrario.
La dimostrazione di questa nuova formulazione della legge di Kirchhoff per le
correnti è semplice. Ogni insieme di taglio partiziona l’insieme di nodi nei due
sotto insiemi N + e N − . Scrivendo le equazioni di Kirchhoff per le correnti per
ciascun nodo del sottoinsieme N + e sommandole membro a membro si ottiene
l’equazione dell’insieme di taglio. Nella somma si eliminano tutte le intensità di
corrente relative ai lati che collegano i nodi del sottoinsieme N + e restano solo
le intensità di corrente relative ai lati che collegano i nodi di N + ai nodi di
N − . Tutte le intensità di corrente i cui riferimenti per i versi vanno dal
sottoinsieme N + al sottoinsieme N − intervengono nella somma con lo stesso
segno e con il segno contrario le intensità di corrente con riferimento opposto.
(Si noti che quando N + contiene un solo nodo e ciò accade quando i lati
dell’insieme di taglio incidono tutti in un solo nodo, l’equazione per l’insieme
di taglio si riduce a quella per il nodo).
Le equazioni per le intensità di corrente degli insiemi di taglio illustrati in
Figura 2.29 sono riportate in Tabella 2.4.
G. Miano, Introduzione ai Circuiti
164
insieme di taglio
T1
T2
T3
T4
T5
T6
Tab. 2.4
2.9
equazione per le intensità di
corrente
−i2 + i4 + i5 = 0
i1 + i4 + i5 = 0
i1 + i2 = 0
i3 − i4 = 0
−i2 + i3 + i5 = 0
i1 + i3 + i5 = 0
Equazioni per gli insiemi di taglio riportati in Figura 2.29
Matrice di incidenza, matrice di maglia ed equazioni di Kirchhoff
Fino a questo momento la relazione di incidenza di un grafo orientato, cioè la
legge di corrispondenza che associa i lati ai nodi, è stata rappresentata
graficamente attraverso elementi geometrici.
2.9.1 Matrice di incidenza
Si consideri un grafo orientato G costituito da n nodi e l lati. È possibile
assegnare la relazione di incidenza del grafo G utilizzando una tabella ordinata
costituita da n righe, quanto sono i nodi, e l colonne, quanti sono i lati, cioè
una matrice rettangolare n × l (in un grafo connesso è sempre l ≥ n −1). A
questa matrice si dà il nome di matrice di incidenza del grafo (circuito) ed è
indicata con A a . Essa è così definita.
Si ordinino i nodi e i lati del grafo orientato associando a ciascuno di essi un
numero naturale: da 1 a n per i nodi e da 1 a l per i lati. La i −esima riga della
matrice di incidenza corrisponda al i −esimo nodo del grafo e lo j − esimo
elemento di questa riga corrisponda al j − esimo lato del grafo. L’elemento aij
di A a (appartenente alla riga i e alla colonna j ), è così definito:
+1
aij = −1
0
se il lato j esce dal nodo “i”;
i = 1, 2, ..., n
se il lato j entra nel nodo “i”;
j =1, 2, ..., l
se il lato j non incide nel nodo “i”.
G. Miano, Introduzione ai Circuiti
(125)
165
Gli elementi +1 e −1 della i −esima riga di A a indicano quali sono i lati che
incidono nell’ i −esimo nodo del grafo; essi possono essere due o più di due, in
generale. Gli elementi +1 e −1 della j − esima colonna indicano quali sono i
due nodi nei quali incide il lato “ j ”.
Si consideri il circuito illustrato in Figura 2.30a; il corrispondente grafo
orientato è illustrato in Figura 2.30b. Costruiamo la matrice di incidenza. In
questo caso essa ha 4 righe (4 sono i nodi del circuito) e 5 colonne (5 sono i
bipoli del circuito). La matrice di incidenza è:
1 1 0 0 −1
−1 0 0
1 0
Aa =
0 0 −1 −1 1
0 −1 1 0 0
(⇐ nodo “1”)
(⇐ nodo “2”)
(⇐ nodo “3”)
(⇐ nodo “4”)
(126)
C’è una corrispondenza biunivoca tra il “disegno” illustrato in Figura 2.30a,
che rappresenta il modo in cui i bipoli sono collegati tra loro nel circuito in
esame, il disegno del corrispondente grafo orientato riportato in Figura 2.30b e
la matrice di incidenza (126): essi sono una diversa rappresentazione della
relazione di incidenza che descrive come i bipoli del circuito incidono nei nodi
e, quindi, come sono collegati tra loro.
“1”
“4”
“1”
2
“4”
2
1
5
3
4
“3”
“2”
(a)
Fig. 2.30
“2”
4
(b)
“3”
(a) Circuito di bipoli orientato; (b) grafo orientato corrispondente.
Siccome ogni lato è collegato a due soli nodi, solo due elementi di ciascuna
colonna della matrice di incidenza sono diversi da zero: uno di essi vale +1
(corrisponde al nodo dal quale la punta della freccia del lato orientato esce) e
l’altro vale −1 (corrisponde al nodo nel quale la punta della freccia del lato
orientato entra). Dunque, in ciascuna colonna della matrice di incidenza
abbiamo un solo +1, un solo −1 e gli altri elementi sono tutti nulli. Ne
G. Miano, Introduzione ai Circuiti
166
consegue che la somma di tutte le righe della matrice di incidenza è la riga
identicamente nulla (cioè una riga con tutti zeri) e quindi le righe di A a sono
linearmente dipendenti: di conseguenza il rango di A a è minore di n 10 . Ad
esempio, l’ultima riga della matrice (126) può essere ottenuta, senza ispezionare
il grafo, a partire dalle altre tre righe, imponendo che la somma di tutte e
quattro le righe dia una riga identicamente nulla.
Osservazione
La matrice di incidenza ha una proprietà molto interessante che enunceremo ma
non dimostreremo: (n −1) lati corrispondenti a (n −1) colonne di A a
linearmente indipendenti (ogni colonna è associata a un lato) formano un albero
(un albero è definito univocamente se si assegnano gli (n −1) lati che lo
compongono). Questa proprietà può essere utilizzata per realizzare procedure
automatiche al calcolatore per individuare gli alberi e, quindi, i coalberi di un
grafo. Ciò consente di individuare automaticamente un insieme di maglie
fondamentali e, quindi, tutte le maglie di un grafo.
♦
La matrice di incidenza è importante, non solo perché attraverso di essa è
possibile rappresentare in maniera estremamente semplice e sintetica la
relazione di incidenza del grafo di un circuito (particolarmente adatta ad essere
assemblata ed elaborata attraverso algoritmi automatici realizzati utilizzando
calcolatori elettronici), ma soprattutto perché attraverso di essa è possibile
scrivere automaticamente le equazioni di Kirchhoff per le correnti. Come
vedremo, in seguito, attraverso la matrice di incidenza è possibile imporre, in
modo estremamente semplice, elegante ed efficiente, anche le equazioni di
Kirchhoff per le tensioni. La matrice di incidenza di un circuito contiene tutte
le informazioni di cui c’è bisogno per imporre le leggi di Kirchhoff.
Si consideri il circuito di bipoli riportato in Figura 2.30. Applicando la legge di
Kirchhoff per le correnti ai nodi del circuito si ha l’insieme di equazioni
10 Le righe di una matrice sono linearmente dipendenti se almeno una riga della matrice può
essere espressa come combinazione lineare delle altre. Il rango di una matrice può essere
definito come l’ordine massimo dei minori non nulli della matrice. Di conseguenza, il rango
di una matrice rappresenta il massimo numero di colonne e, quindi, di righe linearmente
indipendenti.
G. Miano, Introduzione ai Circuiti
167
i2
nodo “1” i1 +
nodo “2” −i1 + 0 ⋅ i2
nodo “3” 0 ⋅ i1 + 0 ⋅ i2
nodo “4” 0 ⋅ i1 + −i2
+ 0 ⋅ i3 + 0 ⋅ i4
+ 0 ⋅ i3 +
i4
+ −i3 + −i4
+
i3 + 0 ⋅ i4
+ −i5 = 0,
+ 0 ⋅ i5 = 0,
+
i5 = 0,
+ 0 ⋅ i5 = 0.
(127)
Questo insieme di equazioni può essere riscritto, utilizzando il prodotto riga per
colonna tra una matrice e un vettore colonna, nella seguente forma
i1 0
1 1 0 0 −1
i2 0
−1 0 0
1 0
i3 = 0 .
0 0 −1 −1 1
i4 0
0 −1 1 0 0
i5 0
(128)
La prima equazione del sistema (127) è ottenuta moltiplicando la prima riga
della matrice rettangolare 4 × 5 per il vettore colonna con 5 righe (matrice
rettangolare 5 ×1), e imponendo, poi, che tale prodotto sia zero; la seconda
equazione è ottenuta moltiplicando la seconda riga della matrice rettangolare
4 × 5 per il vettore colonna, e imponendo, ancora, che il prodotto sia zero, e
così via.
La matrice 4 × 5 che compare nell’equazione matriciale (128) è proprio la
matrice di incidenza del grafo orientato del circuito riportato in Figura 2.30b,
la cui espressione è data dalla (126). Se si introduce il vettore colonna
rappresentativo delle intensità di corrente del circuito 11 ,
i = i1 ,i2 ,i3 , i4 , i5 ,
(129)
0 = 0,0, 0, 0, 0 ,
(130)
T
e il vettore colonna nullo
T
il sistema di equazioni (128) può essere riscritto, in forma sintetica, come:
11 Per ridurre l’ingombro rappresenteremo i vettori colonna come vettori riga trasposti. In
generale, con il simbolo C T si intende la matrice trasposta della matrice C . Nel caso
particolare in cui C è un vettore riga, cioè una matrice con una sola riga, la trasposta è un
vettore colonna, cioè una matrice con una sola colonna.
G. Miano, Introduzione ai Circuiti
168
Aai = 0 .
(131)
In conclusione, l’insieme di tutte le equazioni di Kirchhoff per le correnti
(equazioni per i nodi) del circuito possono essere ottenute moltiplicando la
matrice di incidenza del circuito per il vettore colonna rappresentativo delle
intensità di corrente del circuito e imponendo che tale prodotto sia il vettore
colonna identicamente nullo.
Questo risultato è del tutto generale, non vale solo per l’esempio che abbiamo
appena considerato. Si consideri un generico circuito con l lati e n nodi e
utilizzando i numeri naturali si ordinino i nodi da 1 a n e i lati da 1 a l .
Introduciamo il vettore colonna rappresentativo delle intensità di corrente del
circuito,
i = i1 ,i2 ,...,il−1 , il ;
T
(132)
esso ha l righe. Siccome gli elementi +1 e −1 di una riga di A a indicano i lati
orientati che incidono nel nodo corrispondente, il prodotto scalare della riga per
il vettore colonna i coincide con la somma algebrica delle intensità di corrente
incidenti il nodo. Allora, il prodotto, riga per colonna, tra la prima riga di A a e
il vettore i è uguale alla somma algebrica delle intensità di corrente incidenti
nel nodo “1”; il prodotto, riga per colonna, tra la seconda riga della matrice A a
e il vettore i è uguale alla somma algebrica delle intensità di corrente incidenti
nel nodo “2”; e così via, fino al prodotto dell’ennesima riga della matrice A a
per il vettore colonna i . Siccome per la legge di Kirchhoff delle correnti la
somma algebrica delle intensità di corrente incidenti in ciascun nodo deve
essere uguale a zero, si ottiene di nuovo l’equazione (131) (in generale, 0 è il
vettore colonna identicamente nullo di dimensione l ). Dunque la conoscenza
della matrice di incidenza consente di determinare immediatamente le equazioni
di Kirchhoff per le correnti per tutti i nodi del circuito.
Osservazione: matrici sparse
La metà degli elementi della matrice di incidenza (126) sono nulli. In generale,
il numero di elementi diversi da zero di una matrice di incidenza è uguale a 2l ,
mentre il numero totale degli elementi è n × l , quindi il numero degli elementi
uguali a zero è (n − 2 ) × l . Se n >> 1, la maggior parte degli elementi della
G. Miano, Introduzione ai Circuiti
169
matrice sono nulli, e quindi sono in un certo senso “ridondanti”. Le matrici in
cui la maggior parte degli elementi sono nulli prendono il nome di matrici
sparse. Quale sia la percentuale di elementi necessaria per fare ritenere una
matrice sparsa, dipende, ovviamente dal contesto.
Lavorare con matrici sparse è un notevole vantaggio nell’elaborazione
automatica delle equazioni circuitali tramite calcolatori, dal momento che
memorizzando solo gli elementi diversi da zero, si possono ottenere notevoli
risparmi di memoria e di operazioni e, quindi, di tempo.
♦
2.9.2 Matrice delle maglie
Le maglie orientate di un grafo possono essere descritte attraverso una relazione
analoga a quella di incidenza, che associa a ciascuna maglia i lati che la
compongono. Questa relazione, così come quella di incidenza, può essere
rappresentata attraverso una matrice, detta matrice delle maglie: le righe sono
associate alle maglie (e sono tante quante sono le maglie distinte del grafo; le
colonne sono associate ai lati e sono tante quante sono i lati del grafo). Si
indichi con m il numero di maglie distinte del grafo (sarà sempre m < l), le si
ordinino associando a ciascuna di esse un numero naturale e le si orientino
assegnando (in maniera arbitraria) un verso di percorrenza. La i −esima riga è
associata alla i −esima maglia e la j − esima colonna è associata al j − esimo
lato. Il generico elemento bij della matrice delle maglie è così definito
(i = 1, m; j = 1, l):
+1 lato j appartiene alla maglia i e i versi sono concordi;
bij = −1 lato j appartiene alla maglia i e i versi sono discordi;
0 se il lato j non appartiene alla maglia i.
(133)
Si consideri di nuovo il circuito illustrato in Figura 2.30a e si costruisca la
matrice delle maglie. Prima di tutto bisogna individuare le maglie. In questo
caso le possibili maglie sono 3 e sono riportate in Figura 2.31. Quindi, la
matrice delle maglie ha 3 righe (quante sono le maglie distinte) e 5 colonne
(quanti sono i lati). Essa vale
G. Miano, Introduzione ai Circuiti
170
−1 1 1 +1 0
B a = 0 0 1 1 −1
−1 1 0 0
1
maglia M1,
maglia M 2,
maglia M 3.
(134)
Le righe della matrice delle maglie sono linearmente dipendenti tra loro.
Infatti, se si sottrae alla prima riga della matrice (134) la seconda e la terza si
ottiene la riga identicamente nulla. Dunque, anche la matrice delle maglie non è
a rango massimo. Ciò è una proprietà generale ed è conseguenza del fatto che,
se si considerano tutte le maglie di un grafo, esse non sono tutte indipendenti
tra loro: solo l − (n −1) sono indipendenti (un insieme di maglie fondamentali o
l’insieme degli anelli).
4
“1”
1
3
“2”
Fig. 2.31
“4” “1”
2
M1
4
“4”
5
“3”
5
3 1
“3”
M2
“1”
“2”
2
M3
“3”
Maglie (orientate) del circuito riportato in Figura 2.30a.
Così come la matrice di incidenza consente di esprime le equazioni di Kirchhoff
per le correnti per tutti i nodi del circuito, la matrice delle maglie consente di
esprimere le equazioni di Kirchhoff per le tensioni per tutte le maglie del
circuito. Si consideri, ora, l’insieme delle equazioni ottenute applicando la
legge di Kirchhoff per le tensioni alle maglie riportate in Figura 2.31,
maglia M1
maglia M2
maglia M 3
−v1 +
v2 +
v3 +
v 4 + 0 ⋅ v 5 = 0,
0 ⋅ v1 + 0 ⋅ v2 +
v3 +
v4 −
v 5 = 0,
−v1 +
v2 + 0 ⋅ v3 + 0 ⋅ v 4 +
v5 = 0.
(135)
È evidente che il sistema di equazioni (135) può essere riscritto nella forma
B av = 0,
G. Miano, Introduzione ai Circuiti
(136)
171
dove B a è la matrice delle maglie (134), v è il vettore colonna rappresentativo
delle tensioni
v = v1 , v 2 , v3 , v4 , v5 ,
T
(137)
e 0 è il vettore colonna identicamente nullo di dimensione 5.
Ovviamente, questo modo di rappresentare le equazioni di Kirchhoff per le
tensioni è del tutto generale e non dipende dal particolare circuito in esame.
Tuttavia, facciamo subito notare che per costruire la matrice delle maglie
bisogna prima determinare tutte le maglie del grafo. Come abbiamo appena
accennato esiste una procedura generale per fare questo. Essa si basa sulla
ricerca automatica di un albero del circuito, ma è molto onerosa dal punto di
vista “computazionale” già per circuiti con poche decine di nodi e di lati.
2.10 Equazioni di Kirchhoff indipendenti
Le equazioni circuitali sono costituite dalle equazioni di Kirchhoff e dalle
equazioni caratteristiche degli elementi circuitali. Le equazioni di Kirchhoff
sono algebriche lineari e omogenee. Invece, le equazioni caratteristiche possono
essere, in generale, algebriche o differenziali, lineari o non lineari, tempoinvarianti o tempo-varianti, omogenee o non omogenee.
Il sistema di equazioni circuitali è, in generale, ben posto?
Un sistema di equazioni si dice ben posto se ammette una e una sola soluzione,
per assegnati termini noti e condizioni iniziali. Condizione necessaria, affinché
un sistema sia ben posto, è che le equazioni indipendenti siano tante quante
sono le incognite del problema, né di più e né di meno.
Le equazioni (algebriche, differenziali, integrali, ...) di un sistema di equazioni sono
dipendenti se almeno una di esse può essere ottenuta combinando le altre o
almeno una parte. Invece, le equazioni del sistema sono indipendenti se e solo se
tutte le equazioni non sono tra loro dipendenti. Inoltre, affinché un problema sia
ben posto non deve mai accadere che due o più equazioni siano tra loro
incompatibili ( (x + y) = 1 e (−x − y) = 0 sono un esempio di due equazioni
incompatibili).
Se il sistema di equazioni circuitali è costituito da un numero di equazioni
indipendenti più grande del numero di incognite o da equazioni incompatibili,
il problema in generale non ammette soluzioni. Invece il sistema ha infinite
G. Miano, Introduzione ai Circuiti
172
soluzioni se il numero di equazioni indipendenti (tra loro compatibili) è più
piccolo del numero di incognite.
Le equazioni caratteristiche sono certamente indipendenti e compatibili tra loro
(ogni equazione caratteristica ha due incognite in esclusiva). Le equazioni
ottenute applicando le leggi di Kirchhoff sono indipendenti? Sono tra loro
compatibili?
2.10.1 Indipendenza delle equazioni di Kirchhoff per le correnti
Si considerino le equazioni di Kirchhoff per le correnti. Analizziamo, come
esempio concreto, le equazioni ottenute applicando la legge di Kirchhoff per le
correnti al circuito rappresentato in Figura 2.30a,
nodo “1” i1 + i2 − i5 = 0,
nodo “2” −i1 + i4 = 0,
nodo “3” −i3 − i4 + i5 = 0,
nodo “4” −i2 + i3 = 0.
(138)
Esse sono linearmente dipendenti. Infatti, sommando membro a membro le 4
equazioni del sistema (138) si ottiene l’identità 0 = 0 (non più un’equazione)12 .
Ciò è un’immediata conseguenza del fatto che la somma di tutte le righe della
matrice di incidenza è la riga identicamente nulla: il rango della matrice di
incidenza A a del circuito di Figura 2.30, data dalla (128), è minore di 4 .
Pertanto la quarta (o qualsiasi altra) equazione del sistema (138) è una
combinazione lineare delle altre tre. Essa può essere ottenuta, prima sommando
membro a membro le altre tre, e poi cambiando il segno di entrambi i membri.
Dunque tutte le “informazioni” contenute nella quarta (o in qualsiasi altra)
equazione del sistema (138) sono già presenti nelle altre tre e, quindi, essa è
ridondante.
Questo risultato è del tutto generale. Le n equazioni di Kirchhoff per le
correnti (n è il numero di nodi),
A a i = 0,
(139)
12 L’uguaglianza f (x1 , x 2 ,...,x n ) = 0 è un’identità se essa verificata per qualsiasi ennupla
x1 , x2 ,..., xn ; invece, se è verificata solo per alcuni valori di x1 , x2 ,..., xn (l’insieme di questi
valori può essere finito oppure infinito), allora essa è un’equazione.
G. Miano, Introduzione ai Circuiti
173
di un circuito con grafo connesso sono linearmente dipendenti, qualunque sia il
grafo del circuito (se si sommano membro a membro le n equazioni del sistema
(139), si ottiene sempre l’identità 0 = 0 ). Ciò è sempre conseguenza del fatto
che la somma di tutte le righe della matrice di incidenza è la riga identicamente
nulla. Questo risultato è in accordo con il fatto che il rango della matrice di
incidenza A a è minore di n . È ovvio, a questo punto, che una qualsiasi
equazione del sistema (139), o del sistema (138), può essere eliminata, senza
che l’informazione contenuta nel sistema ne risenta in alcun modo.
Quante e quali sono le equazioni di Kirchhoff per le correnti linearmente
indipendenti?
Proprietà di indipendenza delle equazioni di Kirchhoff per le correnti
Per un circuito con grafo connesso con n nodi, n − 1 equazioni di Kirchhoff
per le correnti, scelte in maniera arbitraria tra le possibili n , sono linearmente
indipendenti.
♦
Analizziamo di nuovo, come esempio concreto, le equazioni di Kirchhoff per le
correnti del circuito di Figura 2.30a, il sistema (138). Un insieme costituito da
tre equazioni del sistema (138), scelte in modo qualsiasi, ad esempio, dalle
prime tre equazioni, è un insieme di equazioni linearmente indipendenti. Infatti,
le prime due equazioni del sistema (138) non possono essere dipendenti tra loro
perché, ad esempio, i5 compare solo nella prima e non nella seconda.
Condizione sufficiente affinché una equazione di un certo insieme sia
indipendente dalle altre, è che nell’equazione vi sia almeno una incognita in
esclusiva. Ciò può essere dedotto sia ispezionando direttamente le due
equazioni, sia osservando che, se si considera l’insieme dei nodi “1” e “2” e
l’insieme dei restanti nodi, cioè “3” e “4”, il lato 5 collega un nodo del primo
insieme a un nodo del secondo (il grafo è connesso). Di conseguenza l’intensità
di corrente di quel lato comparirà soltanto in una sola delle prime due
equazioni. Lo stesso ragionamento vale per l’insieme costituito dalla prima e
dalla terza equazione e per l’insieme costituito dalla seconda e dalla terza
equazione. Inoltre, bisogna mostrare, anche, che la prima equazione è
indipendente dalla seconda e dalla terza. Il lato 2 collega il nodo “1” al nodo
“4” e quindi l’intensità di corrente di quel lato comparirà soltanto in una sola
G. Miano, Introduzione ai Circuiti
174
delle prime tre equazioni del sistema (138), di conseguenza l’equazione relativa
al nodo “1” è indipendente dalle equazioni relative al nodo “2” e “3”. Lo stesso
ragionamento possiamo ripeterlo per gli altri possibili sotto insiemi. In
conclusione, comunque si scelgano tre equazioni del sistema (138) esse sono
sempre tra loro linearmente indipendenti.
Osservazione
La proprietà di indipendenza delle equazioni di Kirchhoff per le correnti può
essere dimostrata per un generico circuito connesso, con n nodi e l bipoli,
procedendo in questo modo. Si parte negando la tesi e si dimostra che ciò dà
luogo a un risultato che contraddice l’ipotesi. Questa è la classica dimostrazione
per assurdo.
“1”
“2”
“h−1”“h”
. . ..
parte restante del circuito
Fig. 2.32
Grafo usato per illustrare che n −1 equazioni di Kirchhoff per le correnti sono
indipendenti.
Si assuma, senza perdere di generalità, che le prime h equazioni, con
h ≤ (n −1),
nodo “1” f1 (i1 , i2 , ...,il ) = 0,
nodo “2” f2 (i1 ,i2 ,...,il ) = 0,
.......................
nodo “h” fh (i1 ,i2 ,...,il ) = 0,
(140)
di n − 1 equazioni ottenute applicando la legge di Kirchhoff per le correnti a
n − 1 nodi siano linearmente dipendenti; con il simbolo f j (i1 ,i2 ,...,il ) indichiamo
la somma algebrica delle intensità delle correnti che incidono nel nodo “ j ”.
G. Miano, Introduzione ai Circuiti
175
Inoltre, indichiamo l’insieme dei nodi “1”, “2”, ..., “h” con N h e con N n −h
l’insieme dei restanti nodi. Poiché il grafo è connesso, esiste almeno un bipolo
che collega un nodo dell’insieme N h a un nodo dell’insieme N n −h , Figura
2.32. Pertanto l’intensità di corrente di quel lato compare in una e una sola
equazione dell’insieme (140), e quell’equazione, quindi, non può mai essere
espressa come combinazione lineare delle restanti equazioni dell’insieme (140).
Tale contraddizione si ha per ogni insieme di h nodi con h ≤ (n −1). Quindi le
n − 1 equazioni di Kirchhoff per le correnti sono linearmente indipendenti.
♦
2.10.2 Matrice di incidenza ridotta
Si considerino, senza perdere di generalità, le equazioni ottenute applicando la
legge di Kirchhoff per le correnti ai nodi “1”, “2”, ..., “n − 1”. Esse
costituiscono un insieme massimale di equazioni di Kirchhoff per le correnti
linearmente indipendenti. Si elimini dalla matrice di incidenza A a la riga
corrispondente al nodo “n”, il nodo per il quale non si considera l’equazione di
Kirchhoff per le correnti. Si ottiene, così, la matrice di incidenza ridotta A ;
essa ha n − 1 righe e l lati.
Le equazioni di Kirchhoff per le correnti relative ai nodi “1”, “2”, ..., “n − 1”
possono essere espresse in forma matriciale come
Ai = 0 .
(141)
Il rango di A è n − 1, cioè essa è una matrice a rango massimo. Analizziamo di
nuovo, come esempio concreto, le equazioni di Kirchhoff per le correnti del
circuito di Figura 2.30a. Per questo circuito un insieme massimale di equazioni
di Kirchhoff per le correnti linearmente indipendenti è
nodo “1” i1 + i2 − i5 = 0,
nodo “2” −i1 + i4 = 0,
nodo “3” −i3 − i4 + i5 = 0,
(142)
e la corrispondente matrice di incidenza ridotta è
G. Miano, Introduzione ai Circuiti
176
1 1
0 0 −1
A = −1 0 0 1 0
0 −1 1 0 0
(⇐ nodo “1”)
(⇐ nodo “2”).
(⇐ nodo “3”)
(143)
2.10.3 Indipendenza delle equazioni di Kirchhoff per le tensioni
Si considerino, ora, le equazioni di Kirchhoff per le tensioni. Analizziamo,
come esempio concreto, le equazioni ottenute applicando la legge di Kirchhoff
per le tensioni al circuito rappresentato in Figura 2.30a,
maglia M1
maglia M2
maglia M 3
−v1 + v2 + v3 + v4 = 0,
v3 + v4 − v5 = 0,
−v1 + v2 + v5 = 0.
(144)
Queste equazioni non sono tra loro linearmente indipendenti. Ad esempio, la
terza equazione (o una qualsiasi altra equazione) è combinazione lineare delle
restanti due equazioni. La terza equazione può essere ottenuta sottraendo
membro a membro le prime due, quindi tutte le “informazioni” contenute in
essa sono già presenti nelle prime due. Ciò è un’immediata conseguenza del
fatto che la somma della seconda e terza riga della matrice (134) è uguale alla
prima riga: il rango della matrice di maglia (134) è minore di 3. Invece, le
prime due equazioni del sistema (144) sono linearmente indipendenti, così
come sono linearmente indipendenti la prima e la terza equazione, e la seconda
e la terza equazione. Infatti, le maglie M1 e M2 costituiscono un insieme di
maglie fondamentali del circuito (vedi Figura 2.31): ognuna di esse ha almeno
un lato in esclusiva, quindi le relative equazioni per le tensioni hanno almeno
una tensione incognita in esclusiva e di conseguenza sono linearmente
indipendenti. Lo stesso ragionamento vale per gli altri insiemi di maglie
fondamentali.
È ovvio, a questo punto, che una qualsiasi equazione del sistema (144) può
essere eliminata, senza alterare il contenuto di informazione del sistema stesso
e, quindi, due sono le equazioni linearmente indipendenti di Kirchhoff per le
tensioni.
Si consideri, ora, un generico circuito con m maglie distinte. Le m equazioni
di Kirchhoff per le tensioni corrispondenti
G. Miano, Introduzione ai Circuiti
177
B av = 0,
(145)
sono linearmente dipendenti. In generale, quante e quali sono le equazioni di
Kirchhoff alle tensioni linearmente indipendenti?
Proprietà di indipendenza delle equazioni di Kirchhoff per le tensioni
Per un circuito con grafo connesso con n nodi e l lati, le l − (n − 1) equazioni
di Kirchhoff per le tensioni relative a un insieme di maglie fondamentali sono
linearmente indipendenti. Le equazioni di Kirchhoff per le altre maglie del
circuito possono essere espresse come combinazioni lineari delle equazioni per
le maglie fondamentali.
♦
La proprietà di indipendenza può essere dimostrata semplicemente, anche nel
caso generale, ricordando che ogni maglia di un insieme di maglie fondamentali
ha almeno un lato in esclusiva. Di conseguenza, ogni equazione dell’insieme
delle equazioni di Kirchhoff per un insieme di maglie fondamentali ha almeno
una tensione incognita in esclusiva, e quindi le l − (n − 1) equazioni per le
maglie di un insieme di maglie fondamentali sono linearmente indipendenti.
L’insieme delle equazioni per le tensioni ottenute applicando la legge di
Kirchhoff a un insieme di maglie fondamentali è il più grande insieme di
equazioni linearmente indipendenti per le tensioni (cioè un sottoinsieme
massimale e linearmente indipendente delle equazioni (145))?
La risposta è si. Tali equazioni contengono tutte le informazioni concernenti i
vincoli imposti dalle equazioni di Kirchhoff per le tensioni. Infatti, se si
considera una maglia non fondamentale, essa può essere sempre ottenuta
attraverso “l’unione” di almeno due maglie fondamentali. Si consideri, ad
esempio, il circuito illustrato in Figura 2.30a: la maglia M3 si può ottenere
unendo le due maglie fondamentali M1 e M2 , vedi Figura 2.31. Pertanto,
l’equazione per la maglia M3 si può ottenere combinando linearmente le
equazioni relative alle maglie fondamentali M1 e M2 delle quali M3 è l’unione
(si noti che le tensioni relative ai lati in comune delle maglie fondamentali
vengono eliminate).
G. Miano, Introduzione ai Circuiti
178
Osservazione
Nel caso in cui il grafo è planare, un sottoinsieme massimale e linearmente
indipendente di equazioni indipendenti per le tensioni può essere ottenuto
applicando la legge di Kirchhoff per le tensioni agli anelli del grafo. Le maglie
M2 e M3 riportate in Figura 2.31 sono i due anelli del circuito di Figura 2.30a.
Gli anelli in un grafo planare con n nodi e l lati sono l − (n − 1) .
♦
2.10.4 Matrice di un insieme di maglie fondamentali
Si considerino, senza perdere di generalità, le equazioni ottenute applicando la
legge di Kirchhoff per le tensioni a un insieme di maglie fondamentali. Esse
costituiscono un insieme massimale di equazioni di Kirchhoff per le tensioni
linearmente indipendenti. Si elimini dalla matrice delle maglie B a le righe
corrispondenti alle altre maglie del circuito. Si ottiene, in questo modo, la
matrice di un insieme di maglie fondamentali B ; essa ha l − (n − 1) righe e l
colonne. Allora, le equazioni di Kirchhoff per le tensioni relative a un insieme
di maglie fondamentali possono essere espresse in forma matriciale come
Bv = 0.
(146)
Il rango di B è l − (n − 1) , cioè essa è una matrice a rango massimo.
Analizziamo di nuovo, come esempio concreto, le equazioni di Kirchhoff per le
tensioni del circuito di Figura 2.30a. Per questo circuito un insieme massimale
di equazioni di Kirchhoff per le tensioni linearmente indipendenti è
maglia M1 −v1 + v2 + v3 − v 4 = 0
maglia M2 v3 + v4 − v5 = 0
(147)
e la matrice dell’insieme delle maglie fondamentali corrispondente è
B=
−1 1 1 −1 0
.
0 0 1 1 −1
G. Miano, Introduzione ai Circuiti
(148)
179
Esistono procedure generali per costruire le matrici degli insiemi delle maglie
fondamentali di un assegnato circuito. Esse si basano sulla ricerca automatica di
un albero del circuito secondo la procedura descritta al termine del § 2.8.1.
Come abbiamo avuto modo di osservare, queste procedure sono molto onerose
dal punto di vista “computazionale” già per circuiti con poche decine di nodi e
di lati.
2.11 Il sistema di equazioni fondamentali
Si consideri un circuito connesso con n nodi e l bipoli. Le incognite del
circuito sono le intensità di corrente e le tensioni di ciascun bipolo, quindi sono
l intensità di corrente e l tensioni.
Le equazioni circuitali fondamentali sono costituite da:
(a) n − 1 equazioni linearmente indipendenti per le intensità di corrente,
Ai = 0 , ottenute applicando la legge di Kirchhoff per le correnti a n − 1
nodi qualsiasi del circuito;
(b) l − (n − 1) equazioni linearmente indipendenti alle tensioni, Bv = 0,
ottenute applicando la legge di Kirchhoff per le tensioni a l − (n − 1)
maglie fondamentali del circuito (agli l − (n − 1) anelli se il grafo del
circuito è planare);
(c) l equazioni caratteristiche indipendenti.
Pertanto, le equazioni linearmente indipendenti
dall’applicazione delle leggi di Kirchhoff sono l ,
(n −1)+ [l − (n − 1)] = l.
↑
↑
LKC
LKV
che
si
ottengono
(149)
A queste equazioni diamo il nome di equazioni di interconnessione perché
dipendono solo da come gli elementi circuitali sono tra loro collegati. Esse sono
algebriche, lineari e omogenee; inoltre, sono tutte linearmente indipendenti
perché nelle equazioni Ai = 0 compaiono solo le intensità di corrente e nelle
equazioni Bv = 0 compaiono solo le tensioni (e quindi sono anche compatibili
tra loro).
G. Miano, Introduzione ai Circuiti
180
Le equazioni caratteristiche possono essere sia di tipo algebrico che di tipo
differenziale, a seconda della natura del bipolo. Se il circuito è costituito da soli
elementi resistivi e generatori, le equazioni circuitali sono di tipo algebrico. Se
nel circuito ci sono anche elementi dinamici, allora le equazioni circuitali sono
di tipo algebrico-differenziale.
In conclusione, l’insieme delle equazioni di interconnessione e delle equazioni
caratteristiche è un sistema di 2l equazioni in 2l incognite. Esso è un insieme
di equazioni indipendenti ? 13 Le equazioni di interconnessione sono
compatibili con le equazioni caratteristiche? Fatta eccezione di pochi casi,
molto particolari, le equazioni di interconnessione e le equazioni caratteristiche
sono tra loro indipendenti e compatibili.
Esempio
Ora applicheremo i risultati che abbiamo appena ottenuto a un circuito di
resistori lineari e generatori ideali. Si consideri il circuito illustrato in Figura
2.33. Esso è costituito da tre resistori lineari e da due generatori indipendenti
uno di tensione sinusoidale, e(t ) = Em sin(2πft) e uno di corrente stazionario,
j(t ) = I 0 . I parametri del circuito sono riportati in Tabella 2.5. Si determinino
le intensità di corrente e le tensioni del circuito.
R1 = 1 Ω
Tab. 2.5
R2 = 2 Ω
R3 = 2
f = 1 kHz
Em = 1 V
I0 = 1 A
Parametri del circuito di Figura 2.33
Il circuito è costituito da 5 bipoli. Si fissino i riferimenti per i versi delle
intensità di corrente, come è indicato in Figura 2.33b, e si assuma per ciascun
bipolo la convenzione dell’utilizzatore. Di conseguenza sono fissati anche i
versi di riferimento per le tensioni. La prima operazione che bisogna fare
quando si imposta la soluzione di un circuito è assegnare i versi di riferimenti
delle intensità di corrente e tensioni.
Le incognite del problema sono le 5 intensità di corrente i1 , i2 , ..., i5 e le 5
tensioni v1 , v2 , ..., v5 . In realtà la tensione del generatore di tensione e
13 Siano E1 ed E 2 due insiemi di equazioni, ciascuno dei quali costituito da sole equazioni
compatibili e indipendenti. In generale, le equazioni ottenute dall’unione di E1 ed E 2
possono essere incompatibili e/o dipendenti.
G. Miano, Introduzione ai Circuiti
181
l’intensità di corrente del generatore di corrente non sono delle vere incognite,
anche se formalmente e per il momento conviene considerarle come tali.
Fig. 2.33
Circuito resistivo lineare (a), circuito orientato (b) e grafo orientato
corrispondente (c).
Fig. 2.34
Un albero del grafo di Figura 2.33c, coalbero e insieme di maglie fondamentali
corrispondenti.
Ora bisogna cercare le equazioni di interconnessione indipendenti. A tale scopo
è utile riferirsi al grafo orientato riportato in Figura 2.33c.
Il circuito in questione ha tre nodi (i nodi “1”, “2” e “3”), quindi è possibile
scrivere solo due equazioni di Kirchhoff per le correnti linearmente
indipendenti (si scelgano le equazioni relative ai nodi “1” e “2”)
nodo “1” i1 − i5 = 0,
nodo “2” i1 − i2 − i3 + i4 = 0.
(150)
Ora bisogna determinare le equazioni di Kirchhoff indipendenti per le tensioni.
A tale scopo si costruisca un insieme di maglie fondamentali. In Figura 2.34 è
G. Miano, Introduzione ai Circuiti
182
illustrato un albero del grafo di Figura 2.33c, insieme ai lati del coalbero e alle
tre maglie fondamentali relative all’albero che è stato scelto. Applicando la
legge di Kirchhoff per le tensioni alle maglie fondamentali M1 , M2 e M3 si
ottiene l’insieme di equazioni linearmente indipendenti
maglia M1
v1 + v 2 + v5 = 0,
maglia M 2
maglia M3
− v2 + v3 = 0,
− v2 − v 4 = 0.
(151)
Il grafo del circuito in esame è planare e le tre maglie M1 , M2 e M3 sono anche
gli anelli del circuito.
Utilizzando le relazioni caratteristiche degli elementi del circuito si ottiene un
altro insieme di equazioni linearmente indipendenti, costituito dalle 5 equazioni
resistore “1”
v1 − R1i1 = 0,
resistore “2”
v2 − R2 i2 = 0,
resistore “3”
v3 − R3 i3 = 0,
geneneratore corrente
i4 = j,
generatore tensione
(152)
v5 = −e.
Unendo i sistemi di equazioni fondamentali (150), (151) e (152) si ottiene il
sistema delle equazioni circuitali relative al circuito in esame. Esso è costituito
da 10 equazioni e in 10 incognite,
i1 − i5 = 0,
i1 − i2 − i3 + i4 = 0.
v1 + v2 + v5 = 0,
−v + v = 0,
3
2
−v2 − v4 = 0,
v1 − i1 = 0,
v2 − 2i2 = 0,
v3 − 2i3 = 0,
i = 1,
4
v5 = −sin (2π1000t ).
(153)
Osservazione
Si introduca il vettore x così definito, x = (i1 , i2 ,...,i5 , v1 , v2 ,...,v5 ) ; allora il
sistema (153) può essere rappresentato sinteticamente attraverso l’equazione
vettoriale lineare
T
G. Miano, Introduzione ai Circuiti
183
Lx = d ,
(154)
dove L è una matrice quadrata 10 ×10 e d è un vettore noto di dimensione 10
dipendente solo dalle sorgenti. La maggior parte degli elementi della matrice L
sono nulli, e quindi è sparsa.
Le equazioni di un qualsiasi circuito, costituito da soli resistori lineari e
generatori indipendenti (e più in generale da elementi lineari di tipo resistivo),
possono essere sempre poste nella forma (154): L è una matrice quadrata
2l × 2l ( l sono i bipoli del circuito), x e d sono due vettori di dimensione 2l .
Pertanto il modello matematico di un circuito resistivo lineare (con questa
espressione intendiamo un circuito di resistori lineari e generatori indipendenti)
è costituito da un sistema di equazioni algebriche lineari.
Il sistema (154) ha una e una sola soluzione se e solo se il sistema omogeneo
associato
Lx = 0
(155)
che descrive il funzionamento del circuito quando i generatori sono spenti, ha
solo la soluzione x = 0. Questa condizione è verificata se e solo se le equazioni
del sistema omogeneo associato sono linearmente indipendenti, cioè se il rango
della matrice L è uguale a 2l . Ciò accade se e solo se le equazioni del sistema
completo (154) sono indipendenti e compatibili tra loro. Nel caso in esame
questa condizione è verificata (anche se non è immediato provarlo).
I metodi di soluzione per i sistemi algebrici lineari vengono, usualmente, divisi
in due gruppi.
I metodi diretti sono i metodi che in assenza di errori di arrotondamento danno
la soluzione esatta in un numero finito di operazioni. I metodi iterativi sono
metodi in cui la soluzione è ottenuta come limite di una successione di soluzioni
di problemi più semplici. Nel seguito faremo un breve accenno ai soli metodi
diretti.
I metodi diretti classici sono: la regola di Cramer, mediante la quale le
soluzioni vengono espresse come quozienti di determinanti di ordine 2l , e il
metodo di eliminazione di Gauss 14 (o metodo della riduzione per sostituzione).
Per valutare il costo computazionale richiesto dai due metodi si considera il
14 Questo metodo è attribuito comunemente a Gauss, anche se nel libro di Valeriano
Comincioli, Analisi Numerica edito dalla McGraw-Hill (1990), si accenna a un esempio 3×3
contenuto in un manoscritto cinese datato più di 2000 anni.
G. Miano, Introduzione ai Circuiti
184
numero di moltiplicazioni coinvolte nei rispettivi algoritmi. Naturalmente, vi
sono anche altri tipi di operazioni, come le addizioni, ma solitamente ci si
riferisce alle moltiplicazioni, in quanto, in generale, più onerose per quanto
riguarda l’aspetto computazionale. Il numero di moltiplicazioni necessarie per
risolvere il sistema attraverso la regola di Cramer è (2l + 1)(2l − 1)2l!, mentre
nel metodo di Gauss il numero di moltiplicazioni è dell’ordine di 8l 3 . Per l = 5
(l’ordine del sistema (110) è 10) il metodo di Gauss richiede all’incirca mille
moltiplicazioni, mentre la regola di Cramer ha bisogno all’incirca di 3.6 10 6
moltiplicazioni; per l = 10 il metodo di Gauss ha bisogno di circa 8000
moltiplicazioni mentre la regola di Cramer richiede all’incirca 2.4 10 18
moltiplicazioni. Usando un calcolatore in grado di realizzare 10 9
moltiplicazioni al secondo si hanno i seguenti tempi di calcolo:
Regola di Cramer ≅ 3⋅10 4 anni;
Metodo di Gauss ≅ 8⋅10 −6 secondi.
Anche per sistemi di modeste dimensioni il metodo di Cramer si rivela, quindi,
impraticabile. Al contrario, il metodo di Gauss permette di risolvere in tempi
ragionevoli sistemi di grosse dimensioni. Sfruttando la natura particolare delle
matrici, quali ad esempio la sparsità e la simmetria, è possibile ridurre
ulteriormente sia la quantità di memoria richiesta, sia il numero di operazioni.
♦
Il sistema (153) sarà risolto utilizzando il metodo di Gauss. L’idea centrale del
metodo di Gauss è la riduzione della dimensione del sistema, cioè del numero
di equazioni, per eliminazione. Essa consiste nel ricavare da una fissata delle 10
equazioni una particolare incognita e nella sua sostituzione nelle equazioni
rimanenti (eliminazione in avanti). La sostituzione fa così diminuire di pari
passo sia il numero di equazioni che il numero di incognite e quindi diminuisce
la dimensione del problema. Iterando il procedimento, si riduce il problema
originario a un problema a una sola equazione in una sola incognita.
Determinata tale incognita, le altre incognite sono successivamente ottenute
mediante una procedura di sostituzione all’indietro.
Operando in questo modo, dopo l’eliminazione in avanti, il sistema (153) è
trasformato nel sistema
G. Miano, Introduzione ai Circuiti
185
i4 = 1,
v 5 = − sin(2πft ),
v = i ,
1 1
v 2 = 2i2 ,
v3 = 2i3 ,
i = i ,
5 1
i3 = i2 ,
2i2 = sin sin(2πft ) − i1 ,
2i1 = sin sin (2πft) −1.
(156)
La soluzione del circuito si ottiene dal sistema (156) attraverso l’eliminazione
all’indietro. Così facendo si ottiene
i1 = 0.5[sin (2π1000t ) − 1], i2 = 0.5[sin(2π1000t ) +1]
i3 = 0.5[sin (2π1000t ) + 1], i4 = 1, i5 = 0.5[sin (2π1000t ) − 1],
v1 = 0.5[sin (2π1000t ) − 1], v 2 = sin(2π1000t ) + 1,
(157)
v3 = sin(2π1000t) +1, v4 = − sin(2π1000t ) − 1, v 5 = − sin(2π1000t ).
Osservazione
È interessante fare qualche considerazione sull’esistenza e unicità della
soluzione di un circuito di resistori lineari e generatori indipendenti. A questo
scopo si considerino i due circuiti illustrati in Figura 2.35 e si scrivano le
rispettive equazioni, (il sistema (158) per il circuito di Figura 2.35a e il sistema
(159) per il circuito di Figura 2.35b),
i1 + i2 + i3 = 0,
v − v = 0,
3
1
v1 − v2 = 0,
v1 = E1 ,
v 2 = E2 ,
v3 − Ri3 = 0,
(158)
G. Miano, Introduzione ai Circuiti
186
e
i1 + i4 = 0,
i + i − i = 0,
2 3 4
v 2 − v3 = 0,
v1 − v3 − v 4 = 0,
v1 = E,
i2 = −J,
v3 − Ri3 = 0,
v 4 + Ri4 = 0.
Fig. 2.35
(159)
Due esempi di modelli circuitali “mal posti”.
Nel primo circuito (Figura 2.35a) abbiamo un resistore e due generatori di
tensione in parallelo; nel secondo circuito (Figura 2.35b) abbiamo un resistore
con resistenza negativa −R e uno con resistenza positiva R .
Nel sistema di equazioni (158) la terza equazione è incompatibile con la quarta
e la quinta (le equazioni del sistema omogeneo associato non sono tutte
indipendenti). Nel sistema di equazioni (159) la seconda equazione è
incompatibile con le ultime cinque (anche in questo caso le equazioni del
sistema omogeneo associato non sono tutte indipendenti). Quindi, entrambi i
sistemi, in generale, non ammettono soluzioni. Nel primo caso si hanno infinite
soluzioni se E1 = E 2 (le equazioni del sistema completo sono compatibili ma
non sono più indipendenti), mentre nel secondo caso si hanno infinite soluzioni
se E = 0 e J = 0.
Queste situazioni “patologiche” non si verificano se si assume che: (a) tutte le
resistenze sono positive; (b) non esistono maglie costituite da soli generatori di
tensione e corto circuiti; (c) non esistono insiemi di tagli costituiti da soli
generatori di corrente e circuiti aperti. Comunque, qualora si verificassero
G. Miano, Introduzione ai Circuiti
187
queste situazioni patologiche, basta introdurre degli opportuni resistori per
ottenere un modello circuitale “ben posto”. Ad esempio, se nel circuito di
Figura 2.35a si introduce un resistore in serie a uno dei due generatori, il
problema non è più mal posto (bisogna sempre tenere presente che il modello
circuitale che si sta analizzando è un modello dell'oggetto fisico, ma non è
l’oggetto fisico). Un modello è mal posto quando non rappresenta in maniera
adeguata l’oggetto fisico, perché sono stati trascurati effetti di fenomeni che
non possono esserlo.
♦
Esercizio
Si determini il sistema di equazioni fondamentali del circuito riportato in
Figura 2.36, e se ne determini la soluzione applicando il metodo di Gauss. I
parametri del circuito sono riportati in Tabella 2.6.
R1
R1
E
Fig. 2.36
R2
J
Circuito di resistori e generatori stazionari.
R1 = 1 Ω
Tab. 2.6
R2
R3
R2 = 2 Ω
R3 = 4
E =1V
J =1 A
Parametri del circuito di Figura 2.35
♦
Osservazione
Abbiamo, solo per semplicità, considerato circuiti di resistori e generatori.
L’analisi svolta si applica senza alcuna difficoltà ai circuiti che contengono
anche elementi dinamici. Per questi circuiti il sistema di equazioni fondamentali
G. Miano, Introduzione ai Circuiti
188
è misto: esso è costituito da equazioni algebriche e da equazioni differenziali. Il
sistema di equazioni fondamentali può essere ridotto a un sistema di sole
equazioni differenziali del primo ordine, tante quanti sono i bipoli dinamici, in
cui le incognite sono le grandezze di stato del circuito, utilizzando ancora il
metodo di Gauss. Ritorneremo su questa questione nel Capitolo 6, dove sarà
approfondita.
♦
2.12 Potenziali di nodo
Le equazioni di interconnessione di un circuito possono essere riformulate
attraverso l’introduzione dei potenziali di nodo e delle correnti di maglia.
Queste grandezze ausiliarie sono alla base di due metodi classici di analisi
circuitale: il metodo dei potenziali di nodo e il metodo delle correnti di maglia.
Il metodo dei potenziali di nodo consiste nell’esprimere le tensioni di ciascun
lato attraverso delle opportune grandezze ausiliarie in maniera tale da imporre
che la legge di Kirchhoff per le tensioni sia verificata automaticamente per ogni
maglia del circuito. Dualmente, il metodo delle correnti di maglia consiste
nell’esprimere le intensità di corrente di ciascun lato attraverso delle opportune
grandezze ausiliarie in maniera tale da imporre che la legge di Kirchhoff per le
correnti sia verificata automaticamente per ogni nodo del circuito.
In queste note presenteremo in dettaglio il metodo dei potenziali di nodo,
perché, come tra poco faremo vedere, attraverso questo metodo si pone rimedio
alla difficoltà derivante dall’elevato costo computazionale necessario per
individuare un insieme di maglie fondamentali del circuito. Invece, per quanto
riguarda il metodo delle correnti di maglia ci limiteremo a descriverne gli
aspetti fondamentali. L’applicazione del metodo delle correnti di maglia
richiede la determinazione di un insieme di maglie fondamentali, quindi. in
generale, il costo computazionale richiesto è molto elevato.
Si consideri un generico circuito, con n nodi e l bipoli, si assegnino i versi di
riferimento per le intensità di corrente e si faccia su ciascun bipolo la
convenzione dell’utilizzatore. Si associ a ciascun nodo del circuito un
potenziale di nodo: al generico nodo “ i ” ( i = 1, 2,...,n ) si associ il potenziale di
nodo ei . Per esemplificare, faremo riferimento a un circuito con un grafo del
tipo illustrato in Figura 2.36a.
G. Miano, Introduzione ai Circuiti
189
Si assuma, ora, che sia possibile esprimere la tensione di ciascun bipolo del
circuito in funzione dei potenziali dei due nodi nei quali il lato incide secondo
la seguente regola (vedi Figura 2.36b): la tensione vs del generico lato s
(s = 1, 2,...,l ) del circuito è espressa come differenza tra il potenziale del nodo
marcato con il segno “+ ” (da cui esce la freccia che indica il verso di
riferimento dell’intensità di corrente) e il potenziale del nodo marcato con il
segno “ − ” (in cui entra la freccia che indica il verso di riferimento
dell’intensità di corrente),
v s = e p − e q per s = 1, 2,...,l .
(160)
vs
Fig. 2.36
Potenziali di nodo.
Osservazione
È evidente che, una volta stabilita la stessa convenzione per tutti i bipoli, ad
esempio, quella dell’utilizzatore, per scrivere le relazioni (160), con i segni
corretti, sono sufficienti i versi di riferimento delle sole intensità di corrente: la
tensione v s del generico lato s ( s = 1, 2,...,l ) del circuito è espressa come
differenza tra il potenziale del nodo da cui esce la freccia che indica il verso di
riferimento dell’intensità di corrente is (il verso con cui è stato orientato il lato
del grafo corrispondente), e il potenziale del nodo in cui entra la freccia che
indica il verso di riferimento dell’intensità di corrente.
♦
Le tensioni espresse attraverso la (160) verificano automaticamente la seconda
legge di Kirchhoff qualunque siano i valori dei potenziali di nodo e1 , e2 , ...,
en .
G. Miano, Introduzione ai Circuiti
190
Verifichiamo subito questa affermazione riferendoci, ad esempio, al circuito il
cui grafo è riportato in Figura 2.36a. Si consideri, ad esempio, la maglia
costituita dai lati 1, 2, 3, 4 e 7, riportata in Figura 2.37 e si determini la
corrispondente equazione di Kirchhoff per le tensioni. Si ottiene l’equazione
v1 + v2 − v3 − v4 − v7 = 0.
(161)
Si esprimano le tensioni dei lati 1, 2, 3, 4 e 7 attraverso i potenziali di nodo
secondo la (160),
v1 = e5 − e1 , v2 = e1 − e2 , v3 = e3 − e2 , v4 = e4 − e3 , v7 = e5 − e4 .
(162)
Sostituendo le (162) nella (161) si ottiene:
(e5 − e1 ) + (e1 − e2 ) − (e3 − e2 ) − (e4 − e3 ) − (e5 − e4 ) = 0 .
(163)
L’uguaglianza (163) è l’identità 0 = 0 , cioè essa è sempre verificata,
indipendentemente da valori dei potenziali di nodo e1 , e2 , ..., e5 . Di
conseguenza le tensioni v1 , v2 , v3 ,v 4 e v7 espresse attraverso le (162) verificano
automaticamente l’equazione di Kirchhoff (161), indipendentemente dai valori
dei potenziali di nodo e1 , e2 , ..., e5 .
Questa è una proprietà generale, indipendente dal circuito e dalla maglia
considerata nel circuito. Essa deriva dal fatto che ogni maglia definisce un
cammino chiuso, pertanto nella somma algebrica delle tensioni il potenziale di
ogni nodo appartenente alla maglia compare due volte, una volta con il segno +
e una volta con il segno −.
Proprietà
Se le tensioni di un circuito sono espresse in termini di potenziali di nodo
attraverso la relazione (160), allora esse verificano automaticamente la legge di
Kirchhoff per le tensioni.
♦
G. Miano, Introduzione ai Circuiti
191
Osservazione
Questo risultato è importante solo se le tensioni del circuito possono essere
sempre effettivamente rappresentate come differenza tra due potenziali secondo
la relazione (160). La questione può essere formalizzata nel modo seguente: si
supponga che siano note le tensioni v1 , v2 ,...,vl del circuito in esame. È possibile
determinare n potenziali di nodo e1 ,e 2 , ...,en in modo tale che per ogni bipolo
sia verificata la (160) ?
Fig. 2.38
Un albero e corrispondente coalbero del grafo rappresentato in Figura 2.36a.
Con riferimento all’esempio riportato in Figura 2.36b ciò si traduce nella
seguente questione: il sistema di equazioni
e5 − e1 = v1 , e1 − e2 = v2 , e3 − e2 = v3 , e4 − e3 = v4 ,
e5 − e 4 = v5 , e5 − e4 = v6 , e 5 − e4 = v 7 ,
(164)
in cui le tensioni sono da considerarsi come termini noti, ammette sempre una
soluzione? Questo sistema potrebbe non ammettere soluzioni se alcune
equazioni fossero tra loro incompatibili. Come ora faremo vedere, il sistema
(164) ammette sempre soluzioni e il numero di esse è infinito se le tensioni
verificano la legge di Kirchhoff per le tensioni.
Conviene affrontare questo problema utilizzando la teoria dei grafi piuttosto
che risolvere direttamente il sistema (164). L’insieme dei potenziali di nodo
e1 ,e 2 , ...,e5 corrispondente a un generico insieme di tensioni v1 , v2 ,...,v7
compatibili con la legge di Kirchhoff può essere determinato in questo modo.
Si consideri un albero del grafo di Figura 2.36a, ad esempio quello
rappresentato in Figura 2.38a e il corrispondente coalbero, Figura 2.38b. Si
G. Miano, Introduzione ai Circuiti
192
assuma, per il momento, che sia possibile assegnare un valore arbitrario, che
indichiamo con e0 (potenziale di riferimento), per esempio, al potenziale del
nodo “5” (nodo di riferimento),
e5 = e 0 ;
(165)
si passi al nodo “4”, contiguo al nodo “5” e si scelga il potenziale e4 in modo
tale che sia verificata la (160),
e4 = e0 − v 7 ;
(166)
si considerino ora i nodi contigui al nodo “4” e si scelgano i potenziali e1 , e2
ed e3 in modo tale che sia verificata ancora la (160),
e1 = e 4 − v6 ,
e2 = v5 − e4 ,
e3 = e4 − v4 .
(167)
Abbiamo già un primo risultato notevole: i potenziali di nodo, a meno di una
costante additiva rappresentata dal potenziale di riferimento, sono
completamente determinati dalle tensioni dei bipoli corrispondenti ai lati
dell’albero.
Questo risultato non dipende dal particolare circuito in esame. Esso è solo
conseguenza del fatto che due lati distinti di un qualsiasi albero incidono
almeno in due nodi diversi (se ciò non fosse ci sarebbero delle maglie
nell’albero).
Se si sceglie un altro nodo come nodo di riferimento o un altro albero si ottiene
un altro insieme di potenziali di nodo che differisce da quello che abbiamo
appena ottenuto solo per una costante additiva. Il lettore verifichi tale proprietà.
Tutte le tensioni dei lati di coalbero sono esprimibili attraverso le relazioni
(160) in funzione dei potenziali di nodo dati dalle espressioni (165)-(167).
Infatti, applicando la legge di Kirchhoff per le tensioni alle maglie
fondamentali corrispondenti al coalbero di Figura 2.38b si ottengono le
relazioni
G. Miano, Introduzione ai Circuiti
193
v1 = v6 + v7 = (e4 − e1 ) + (e5 − e4 ) = e 5 − e1 ,
v 2 = v5 − v6 = (e4 − e2 ) − (e4 − e1 ) = e1 − e2 ,
v3 = v5 − v 4 = (e4 − e2 ) − (e4 − e 3 ) = e3 − e 2 .
(168)
Anche questo risultato è generale e non dipende dal particolare circuito in
esame. Applicando la legge di Kirchhoff alle l − (n − 1) maglie fondamentali
del circuito è possibile esprimere sempre tutte le tensioni di coalbero in
funzione delle sole tensioni di albero. Ora se si esprimono queste ultime in
termini di potenziali di nodo attraverso la relazione (160), si ha
immediatamente che anche ogni tensione di coalbero verifica la relazione
(160). Infatti ogni maglia fondamentale è costituita da un solo lato di coalbero
e i restanti lati sono solo di albero. Inoltre, nella somma algebrica delle tensioni
di albero di una qualsiasi maglia fondamentale, i potenziali dei due nodi nei
quali il lato di coalbero incide compaiono una sola volta, mentre i potenziali
degli altri nodi compaiono due volte, una volta con il segno + e una volta con
il segno − .
♦
Osservazione
C’è un profondo legame tra la rappresentazione delle tensioni di un circuito
attraverso i potenziali di nodo e la rappresentazione del campo elettrico nel
modello quasi-stazionario elettrico attraverso il gradiente di una funzione
potenziale scalare. In entrambi i casi introducendo una grandezza ausiliaria si
riesce a imporre automaticamente la conservazione di una “circuitazione”: nel
modello quasi-stazionario elettrico, esprimendo il campo elettrico attraverso il
gradiente del potenziale elettrico scalare, si impone naturalmente che il campo
sia conservativo rispetto alla circuitazione. In realtà c’è un legame ancora più
profondo tra questi due rappresentazioni: il potenziale di ogni nodo di un
circuito coincide, a meno di una costante additiva arbitraria, con il potenziale
scalare elettrico della giunzione metallica che il nodo rappresenta.
♦
La relazione tra le tensioni e i potenziali di nodo di un circuito può essere
espressa, in generale, attraverso la matrice di incidenza. Si introduca a questo
T
proposito il vettore dei potenziali di nodo e a = (e1 , e2 ,...,en ) . La relazione tra il
vettore delle tensioni v ed e a è data da
G. Miano, Introduzione ai Circuiti
194
v = A aT ea
(169)
dove A a T è la matrice trasposta della matrice di incidenza. La j − esima riga
( j = 1,2, ...,l) di A a T corrisponde al j − esimo lato del grafo e coincide con la
j − esima colonna di A a . Essa contiene le informazioni sui nodi nei quali il
j − esimo lato incide: l’elemento della riga corrispondente al nodo da cui il
j − esimo lato orientato esce è uguale a +1, l’elemento della riga
corrispondente al nodo in cui il j − esimo lato orientato entra è uguale a −1 e
gli altri elementi sono tutti nulli. Pertanto il prodotto della j − esima riga di
A a T con il vettore colonna e a è uguale alla differenza tra il potenziale del
nodo da cui il lato j (orientato concordemente con il verso di riferimento per
la corrispondente intensità di corrente), esce e il potenziale del nodo in cui lo
stesso lato entra. Ad esempio, la tensione v1 del lato 1 del circuito il cui grafo è
riportato in Figura 2.36a è data dalla differenza tra il potenziale del nodo “5” e
il potenziale del nodo “1”, v1 = e5 − e1 . Quindi, essa può essere ottenuta,
considerando il vettore riga che si ottiene trasponendo il primo vettore colonna
della matrice di incidenza, −1 0 0 0 +1 , e moltiplicandolo per il vettore
colonna rappresentativo dei potenziali di nodo del circuito,
T
e1 e 2 e3 e 4 e5 .
Esercizio
Il lettore verifichi la relazione (169) per il circuito il cui grafo è riportato in
Figura 2.36a.
♦
Si assuma come riferimento per il potenziale quello del nodo “n ”, lo si ponga
uguale a zero, en = 0 , e si introduca il vettore dei potenziali ridotto
T
e = (e1 , e2 ,...,en −1 ) . In termini del vettore e la (169) diventa
v = ATe
(170)
dove A è la matrice di incidenza ridotta ottenuta eliminando dalla matrice di
incidenza A a la riga corrispondente al n − esimo nodo (cioè l’ultima). Le
tensioni espresse attraverso la (170) verificano automaticamente le equazioni di
G. Miano, Introduzione ai Circuiti
195
Kirchhoff per le tensioni indipendentemente dai valori dei potenziali di nodo.
Pertanto, imporre la (170) è del tutto equivalente a imporre le equazioni di
Kirchhoff per le tensioni. Quindi, le equazioni di interconnessione possono
essere così riformulate
Ai = 0,
v − A T e = 0.
(171)
Il sistema costituito dalle equazioni di interconnessione (171) e dalle equazioni
caratteristiche prende il nome di sistema di equazioni di tableau (esse sono
2l + (n −1) equazioni in altrettante incognite). La caratteristica fondamentale
delle equazioni di tableau è che le equazioni di interconnessione sono formulate
utilizzando la sola matrice di incidenza ridotta, non c’è bisogno di costruire una
matrice di un insieme di maglie fondamentali. Le equazioni di tableau sono alla
base di numerosi simulatori numerici per circuiti.
Esercizio
Si determinino le equazioni di interconnessione (171) per il circuito
rappresentato in Figura 2.36a.
♦
In molti casi (ora vedremo quali) le equazioni di tableau possono essere ridotte,
tramite eliminazione per sostituzione, a un sistema di equazioni di dimensione
notevolmente più bassa in cui le incognite sono solo i potenziali di nodo. I
potenziali di nodo incogniti sono (n −1) mentre le equazioni di tableau sono
2l + (n −1) . Per ridurre si può procedere in questa maniera. Il primo passo nella
procedura di riduzione consiste nel rappresentare tutte le tensioni attraverso i
potenziali di nodo, poi sostituirle nelle equazioni costitutive e infine imporre le
equazioni di Kirchhoff per le correnti. Ricordiamoci sempre che quando si
applica il metodo dei potenziali bisogna imporre esplicitamente le equazioni di
Kirchhoff per le correnti (le equazioni di Kirchhoff per le tensioni non devono
essere imposte).
G. Miano, Introduzione ai Circuiti
196
Esercizio
Per mostrare una applicazione del metodo dei potenziali di nodo e la procedura
di riduzione delle equazioni di tableau, si consideri il circuito di resistori lineari
e di generatori indipendenti illustrato in Figura 2.39; si assumano per i
parametri del circuito i valori riportati in Tabella 2.7.
Il circuito in esame ha 3 nodi e 5 lati. Costruiamo il sistema di equazioni di
tableau del circuito. Assumiamo come nodo di riferimento il nodo “3”, pertanto
poniamo e3 = 0 . Le equazioni di Kirchhoff per le correnti per i nodi “1” e “2”
sono
i1 + i4 = 0 ,
−i1 + i2 + i3 − i5 = 0 .
(172)
(173)
Questo é un insieme massimale di equazioni di Kirchhoff per le correnti
linearmente indipendenti.
+
−
Fig. 2.39
E = 10 V
Tab. 2.7
Il potenziale del nodo “3” è posto uguale a zero.
R1 = 1 Ω
J =1A
R2 = 1 Ω
R2 = 2 Ω
Parametri del circuito di Figura 2.39
Le equazioni che esprimono le tensioni in funzione dei potenziali di nodo sono
v1 = e1 − e2 ,
v 2 = e2 ,
v3 = e 2 ,
v 4 = e1 ,
v 5 = e2 .
G. Miano, Introduzione ai Circuiti
(174)
(175)
(176)
(177)
(178)
197
Infine, le equazioni caratteristiche dei singoli bipoli sono
v1 − R1i1 = 0,
v 2 − R2 i2 = 0,
v3 − R3 i3 = 0 ,
v4 = E ,
i5 = J .
(179)
(180)
(181)
(182)
(183)
Questo sistema di equazioni è algebrico lineare ed è costituito da 13 equazioni
in 13 incognite. Questo sistema può essere risolto utilizzando la tecnica di
riduzione per sostituzione (metodo di eliminazione di Gauss).
La strategia di riduzione ottima la si ottiene sfruttando le proprietà di
connessione del circuito in esame. Risolveremo il problema della riduzione in
questo modo. Osserviamo, innanzi tutto, che il potenziale e1 non è una vera
incognita del problema perché esso è imposto dal generatore di tensione
(avendo scelto e3 = 0 ); quindi abbiamo
e1 = E .
(184)
Pertanto, l’unico potenziale di nodo effettivamente incognito è e2 . L’equazione
per il potenziale di nodo e2 può essere determinata procedendo in questo modo.
Per ogni bipolo collegato al nodo “2” è possibile esprimere l’intensità di
corrente in funzione della tensione e quindi in funzione dei soli potenziali di
nodo (l’intensità di corrente del generatore ideale di corrente è nota, il
potenziale e1 è noto),
i1 =
E − e2
e
e
, i2 = 2 , i3 = 2 .
R1
R2
R3
(185)
Imponendo, ora, la legge di Kirchhoff per le intensità di corrente al nodo “2” si
ottiene l’equazione per e2
−i1 + i2 + i3 − J = 0 ⇒ −
E − e2 e2 e2
+
+
− J = 0.
R1
R2 R3
(186)
Risolvendo l’equazione (1186) si ottiene
G. Miano, Introduzione ai Circuiti
198
J
e2 = E + 1
1
1 .
+
+
R1 R2 R3
(187)
Sostituendo in questa espressione i valori riportati in Tabella. 2.7 si ha
e2 = 4, 4 V .
(188)
Ora siamo in grado di determinare tutte le altre grandezze incognite. Basta
sostituire il valore di e2 appena determinato nelle espressioni (185) per
determinare le intensità di corrente i1 , i2 e i3 . Utilizzando, poi, l’equazione di
Kirchhoff (173) si determina l’intensità di corrente i4 . Infine, le tensioni di
ciascun bipolo si determinano utilizzando le equazioni (174)-(178), che
esprimono le tensioni in funzione dei potenziali.
Osservazione
Nella procedura di riduzione, l’equazione di Kirchhoff per le correnti al nodo
“1” non può essere utilizzata per determinare l’equazione per il potenziale e2
perché in essa compare l’intensità di corrente i4 del generatore ideale di
tensione. L’equazione caratteristica del generatore ideale di tensione non
impone alcun legame tra l’intensità di corrente del generatore e la tensione (il
generatore ideale di tensione è controllato solo in corrente). L’equazione di
Kirchhoff al nodo “1” (o quella al nodo “3”) serve solo per determinare
l’intensità di corrente i4 nel generatore ideale di tensione, una volta note le
altre intensità di corrente.
Come si procede nella riduzione se nel circuito ci sono più generatori
indipendenti di tensione? Ad esempio, a ciascun nodo del circuito è connesso
almeno un generatore ideali di tensione. Si consideri il circuito di Figura 2.40
(i parametri sono gli stessi che abbiamo riportato in Tabella 2.7).
Ovviamente, possiamo scrivere le equazioni di tableau del circuito, e risolverle,
poi, con il metodo della riduzione per sostituzione. Noi, ora, risolveremo
questo circuito senza scrivere l’intero sistema di equazioni di tableau. Anche in
questo circuito il valore del potenziale e1 è noto, perché il generatore ideale di
tensione impone la tensione (abbiamo di nuovo scelto il nodo “3” come nodo di
riferimento e, quindi, e3 = 0 ),
G. Miano, Introduzione ai Circuiti
199
e1 = E .
(189)
Inoltre, siccome i nodi “2” e “3” sono collegati direttamente attraverso un
generatore ideale di tensione si ha
e4 − e2 = E .
(190)
+
−
Fig. 2.40 In questo circuito ad ogni nodo è collegato un generatore di tensione.
I potenziali incogniti sono tre, manca ancora un’equazione. Questa equazione, a
differenza del caso esaminato in precedenza, non può essere ottenuta
direttamente applicando la legge di Kirchhoff per le correnti a un nodo del
circuito, perché ad ogni nodo è collegato un generatore ideale di tensione.
Ricordatevi che non è possibile esprimere l’intensità di corrente di un
generatore ideale di tensione in funzione della tensione utilizzando l’equazione
caratteristica. L’equazione mancante deve essere una equazione che deriva dalla
legge di Kirchhoff per le correnti, in cui non devono comparire le intensità di
corrente dei generatori di tensione. Questa equazione può essere ottenuta
considerando un insieme di taglio del circuito privo di generatori di tensione.
Nel caso in esame un insieme di taglio di questo tipo è costituito dai resistori
“1”, “2” e “3” e dal generatore di corrente. Per questo insieme di taglio
l’equazione per le correnti è
i1 − i2 − i3 + J = 0.
(191)
Osserviamo che l’equazione (191) può essere ottenuta attraverso un’opportuna
combinazione lineare delle equazioni di Kirchhoff ai nodi “2” e “4”,
G. Miano, Introduzione ai Circuiti
200
−i1 + i2 + i5 = 0,
i3 − i5 − J = 0.
(192)
Dall’equazione (191), utilizzando le equazioni caratteristiche dei resistori e le
relazioni che esprimono le tensioni in funzione dei potenziali, otteniamo
l’equazione mancante per i potenziali di nodo,
E e2 e4
−
−
+ J = 0.
R1 R2 R3
(193)
Sostituendo in questa equazione l’espressione di e4 che si ottiene dall’equazione
(190) si ha per e2 l’espressione
1
1
−
J
R1 R3
e2 = 1
+
E
1
1
1 .
+
+
R2 R3
R2 R3
(194)
La difficoltà che abbiamo appena incontrato nasce perché vogliamo ridurre il
sistema di equazioni di tableau alle sole equazioni per i potenziali di nodo; se
risolvessimo direttamente le equazioni di tableau non incontreremmo nessuna
difficoltà di questo tipo.
Per risolvere questo problema non bisogna ricorrere necessariamente agli
insiemi di taglio. E’ sufficiente, nella procedura di riduzione, conservare come
incognite, oltre ai potenziali di nodo, anche tutte le intensità di corrente dei
generatori ideali di tensione. In questo modo otteniamo un sistema di
(n −1) + p equazioni ( p è il numero generatori ideali di tensione) nelle
(n −1) + p incognite costituite dagli (n −1) potenziali di nodo e dalle p
intensità di corrente che attraversano i generatori ideali di tensione. Le
equazioni sono ottenute aggiungendo alle (n −1) equazioni di Kirchhoff per le
correnti le p equazioni costitutive dei generatori ideali di tensione. Questa
procedura di riduzione prende il nome di metodo dei potenziali di nodo
modificati.
♦
G. Miano, Introduzione ai Circuiti
201
2.13 Correnti di maglia
Le equazioni circuitali possono essere riformulate in modo tale che le leggi di
Kirchhoff per le correnti siano imposte naturalmente. Il metodo si fonda
sull’introduzione di (b − n + 1) variabili ausiliarie, dette correnti di maglia. Si
consideri un circuito, il grafo corrispondente e un insieme di maglie
fondamentali orientate (arbitrariamente), Figura 2.41. A ogni maglia
fondamentale orientata del circuito si associ una corrente di maglia e a ciascuna
corrente di maglia si assegni un verso di riferimento concorde con
l’orientazione scelta per la maglia.
Fig. 2.41
Un grafo, un albero (lati a tratto spesso) e le correnti di maglia corrispondenti
alle maglie fondamentali associate all'albero scelto.
Innanzi tutto stabiliamo che una data corrente di maglia “circola” in un dato
lato se il lato appartiene alla maglia fondamentale a cui la corrente di maglia è
associata. E’ evidente che, in generale, più di una corrente di maglia circola in
un dato lato, perché il lato può appartenere a più di una maglia fondamentale.
Si assuma, ora, che l’intensità di corrente del lato possa essere espressa come
somma algebrica di tutte le correnti di maglia che “circolano” in quel lato,
prendendo con il segno + tutte le correnti di maglia con versi di riferimento
concordi con quello dell’intensità di corrente di lato e con il segno − tutte le
correnti di maglia che hanno versi di riferimento discordi,
ik = ∑ h ( ± ) J h .
(195)
Si consideri, ad esempio, il circuito il cui grafo orientato (concordemente con i
versi di riferimento delle intensità di corrente) è riportato in Figura 2.41. È
stato scelto un albero (lati a tratto spesso) e sono indicate le correnti di maglia
J1 , J 2 e J 3 associate alle maglie fondamentali corrispondenti all’albero scelto.
G. Miano, Introduzione ai Circuiti
202
Le intensità di corrente di lato sono espresse tramite le correnti di maglia nel
seguente modo
i1 = J1 , i2 = J 2 , i3 = J 3 , i4 = J 3 ,
i5 = −J 2 −J 3, i6 = −J1 + J 2 , i7 = J1 .
(196)
È immediato verificare che le intensità delle correnti espresse attraverso le
(196) verificano la prima legge di Kirchhoff, indipendentemente dai valori
delle correnti di maglia.
A ogni nodo sono collegati due lati di ogni maglia fondamentale a cui il nodo
appartiene e ogni intensità di corrente ausiliaria “circola” nella maglia
fondamentale corrispondente. Di conseguenza ogni corrente di maglia compare
due e due sole volte in ogni equazione di Kirchhoff per le correnti, una volta
con il segno positivo e una volta con il segno negativo. Pertanto le intensità
delle correnti espresse attraverso le (196) verificano automaticamente la legge
di Kirchhoff per le correnti indipendentemente dai valori delle correnti di
maglia J1 , J 2 e J 3 .
Si consideri, ad esempio, l’equazione di Kirchhoff per il nodo “1” del circuito
il cui grafo è riportato in Figura 2.41, a cui sono collegati i lati 1, 6 e 2. La
corrente di maglia J1 è “entrante” nel nodo quando circola nel lato 1, mentre è
“uscente” quando circola nel lato 6; la corrente di maglia J 2 è “entrante”
quando circola nel lato 6 ed è “uscente” quando circola nel lato 2. L’equazione
di Kirchhoff per il nodo “1”,
−i1 + i2 − i6 = 0
(197)
J1 − J2 + (−J1 + J2 ) = 0 ,
(198)
diventa l’identità
una volta che le intensità di corrente dei lati sono state espresse tramite le
correnti di maglia.
La formulazione basata sulle correnti di maglia è poco vantaggiosa rispetto a
quella basata sui potenziali di nodo, a causa dell’elevato costo computazionale
richiesto per determinazione di un insieme di maglie fondamentali.
G. Miano, Introduzione ai Circuiti
203
Osservazione
Le correnti di maglia, nel caso di un grafo planare, possono essere definite
anche per i (l − n +1) anelli. L’intensità di corrente di ciascun lato può essere
espressa attraverso la somma algebrica delle correnti di anello che “circolano”
nel lato (lambiscono il lato).
♦
Anche per le correnti di maglia si pone la questione fondamentale (che si è
posta per i potenziali di nodo), riguardante la possibilità di poter sempre
rappresentare tutte le intensità di corrente di lato di un circuito attraverso le
correnti di maglia. Siccome le intensità di corrente di lato devono verificare
l’equazione di Kirchhoff per le correnti, esiste sempre un insieme di correnti di
maglia attraverso le quali è possibile esprimere le intensità di corrente di lato
del circuito secondo la regola che prima abbiamo definito. Lasciamo al lettore
la dimostrazione di questa proprietà. Si osservi, inoltre, che in un dato circuito
esistono diversi insiemi di maglie fondamentali e, quindi, esistono diversi
insiemi di correnti di maglia in grado di rappresentare un dato insieme di
intensità di corrente di lato.
Una volta scelto un insieme di correnti di maglia, per determinarle bisogna
prima esprimere tutte le intensità di corrente di lato in funzione delle correnti
di maglia, poi esprimere le tensioni dei bipoli controllati in corrente in
funzione delle correnti di maglia e infine imporre le leggi di Kirchhoff per le
tensioni. Questa è la procedura duale a quella che abbiamo descritto quando
abbiamo trattato il problema del calcolo dei potenziali di nodo.
Problema
Si risolva il circuito riportato in Figura 2.39 e il circuito riportato in Figura
2.40 con il metodo delle correnti di maglia.
♦
G. Miano, Introduzione ai Circuiti
204
2.14 Conservazione delle potenze elettriche
Ora illustreremo una importante proprietà dei circuiti: la conservazione delle
potenze elettriche. Si consideri un circuito C con l bipoli e siano i1 , i2 ,...,il le
intensità delle correnti e v1 , v2 ,...,vl le tensioni; per ogni bipolo i riferimenti per
i versi dell’intensità di corrente e della tensione siano scelti, ad esempio, in base
alla convenzione dell’utilizzatore (Figura 2.42a). La potenza elettrica assorbita
dal k − esimo bipolo (k = 1, 2,...,l ) del circuito è
pk (t ) = ik (t)v k (t ) .
(199)
vk
vk
ik
Fig. 2.42
îk
circuito di
bipoli
circuito di
bipoli
(a)
(b)
(a) Convenzione dell'utilizzatore e (b) convenzione del generatore.
Conservazione delle potenze elettriche
La somma delle potenze elettriche assorbite dai bipoli di un circuito è istante
per istante uguale a zero,
l
l
∑ p (t ) = ∑ i (t )v (t) = 0 .
k
k =1
k
k
(200)
k=1
♦
Questa proprietà, come ora faremo vedere, è solo conseguenza del fatto che le
intensità di corrente e le tensioni del circuito devono verificare le leggi di
G. Miano, Introduzione ai Circuiti
205
Kirchhoff. Essa, quindi, non dipende in alcun modo dalla natura specifica dei
singoli elementi circuitali, e quindi, dalle relazioni caratteristiche dei singoli
elementi.
Dimostrazione
Questa proprietà può essere dimostrata in modo semplice utilizzando i
T
potenziali di nodo. Si introduca il vettore colonna
i = (i1 ,i2 ,...,il )
rappresentativo di tutte le intensità di corrente del circuito, il vettore colonna
T
v = (v1 , v2 ,...,vl ) rappresentativo di tutte le tensioni del circuito e il vettore
colonna e = (e1 , e2 ,...,en −1 ) rappresentativo dei potenziali di nodo del circuito,
avendo scelto come potenziale di riferimento quello del nodo “n ”, en = 0.
L’espressione della somma delle potenze assorbite dai bipoli del circuito può
essere così rappresentata:
T
b
∑v i
k k
= v1i1 + v 2i2 + ...+ vn in = v T i .
(201)
k =1
Dunque, la somma delle potenze elettriche assorbite è uguale al prodotto del
vettore riga v T con il vettore colonna i , secondo la regola “righe× colonne”.
Le tensioni del circuito possono essere rappresentate attraverso i potenziali di
nodo:
v = ATe ,
(202)
dove A è la matrice di incidenza ridotta del circuito (ottenuta non riportando la
riga corrispondente al nodo “n ”). Sostituendo la (202) nella (201) si ha:
b
∑v i
k k
k =1
= v T i = (A T e ) i .
T
(203)
Ricordiamo che: vale l’identità
(Pa )T = a T P T ,
204)
G. Miano, Introduzione ai Circuiti
206
dove P e a sono, rispettivamente, una generica matrice p × m e un generico
vettore colonna con m righe; per definizione di trasposta di una matrice si ha
che
(Q )
T T
= Q;
(205)
vale la proprietà associativa del prodotto riga× colonna,
(a Q )b = a
T
T
(Qb) .
(206)
Utilizzando queste proprietà si ha che la (203) può essere così riscritta come
b
∑v i
= v T i = e T (Ai) .
k k
(207)
k =1
Siccome la legge di Kirchhoff per le correnti impone che Ai = 0 , dalla (207) si
ha
b
∑v i
k k
= v T i = 0.
(208)
k =1
♦
Esempio
Si consideri il circuito di Figura 2.43 (per ogni bipolo è stata fatta la
convenzione dell’utilizzatore Figura 2.43a) e si scriva la conservazione delle
potenze. Si ha
v1i1 + v2 i2 + v 3i3 + v4 i4 + v5 i5 = 0.
(209)
È evidente che i termini a primo membro nella (209) non possono avere lo
stesso segno (a meno che non siano tutti nulli; ciò è certamente impossibile se
nel circuito non esistono correnti). Quindi, alcuni termini sono positivi e altri
sono negativi nell’espressione (209). In ogni circuito la potenza assorbita da
alcuni bipoli è positiva e da altri è negativa.
G. Miano, Introduzione ai Circuiti
207
+
+
+
v2
+
i4
i1
v5
−
+
v1
i3 +
i2
i5
−
i4
i1
v3
v4
v2
i2
v̂4
v̂5
i3
v̂3
i5
−
(a)
Fig. 2.43
+
v1
(b)
(a) Per tutti i bipoli è stata fatta la convenzione dell’utilizzatore; (b) per alcuni
bipoli è stata fatta la convenzione del generatore.
Se per tutti i bipoli del circuito si adotta la convenzione del generatore (Figura
2.43b) abbiamo che la somma delle potenze elettriche generate da tutti i bipoli
della rete è uguale a zero.
È possibile scrivere la conservazione delle potenze elettriche anche quando per
alcuni bipoli si fa la convenzione dell’utilizzatore e per altri, invece, la
convenzione del generatore, Figura 2.43b. Partendo dalla (209) e osservando
che
vˆ3 = −v3 , vˆ 4 = −v4 e vˆ 5 = −v 5 ,
(210)
v1i1 + v2 i2 = vˆ 3i3 + vˆ4 i4 + ˆv5 i5 ⇒ p1 + p2 = ˆp3 + pˆ 4 + pˆ 5 .
(211)
si perviene a
La somma delle potenze assorbite dal resistore e dal condensatore è uguale alla
somma delle potenze erogate dal generatore ideale di tensione, dall’induttore e
dal diodo; con il simbolo ˆp abbiamo indicato la potenza generata.
In generale, in ogni circuito la somma delle potenze assorbite da un certo
insieme di bipoli è uguale, istante per istante, alla somma delle potenze erogate
dalla restante parte dei bipoli, cioè
α
∑p
b
i
i=1
=
∑ pˆ .
j
(212)
j=α +1
G. Miano, Introduzione ai Circuiti
208
2.15 Teorema di Tellegen
La proprietà della conservazione delle potenze elettriche, discussa nel
precedente paragrafo, è una diretta conseguenza delle solo leggi di Kirchhoff.
In conseguenza di ciò, come ora mostreremo, questa proprietà vale anche
quando, invece, della potenza elettrica si considera la potenza virtuale. Come
vedremo la potenza elettrica è un caso particolare di potenza virtuale.
v ′k
v ′′k
ik′
ik′′
circuito di
bipoli C ′
Fig. 2.44
circuito di
bipoli C ′′
Due circuiti diversi che hanno lo stesso grafo
Si considerino due circuiti che hanno lo stesso grafo orientato e, in generale,
elementi diversi; siano l i lati del grafo; i lati sono stati orientati
concordemente con i versi di riferimenti delle intensità di corrente, Figura 2.44.
Per esemplificare, si faccia riferimento all’esempio concreto illustrato in Figura
2.45.
Il primo circuito è indicato con C ′ e il secondo con C ′′ . Si usi per entrambi i
circuiti e per ciascun lato la convenzione dell’utilizzatore. Siano i1′ , i2′ ,...,il′ le
intensità di corrente e v1′ , v2′ ,...,vl′ le tensioni del circuito C ′ e i1′ ,′ i2′ ′,...,il′ ′ le
intensità di corrente e v1′ ′, v2′ ′,...,vl′′ le tensioni del circuito C ′′ . Le matrici di
incidenza dei due circuiti sono uguali perché hanno lo stesso grafo e le si
indichi con A .
Si considerino, ora, le intensità di corrente del circuito C ′ e le tensioni del
circuito C ′′ (o viceversa). Per il k − esimo lato ( k = 1, 2,...,l ) del grafo dei due
circuiti si definisce la potenza virtuale assorbita dal lato come
Pk = ik′ v k′ ′ .
G. Miano, Introduzione ai Circuiti
(213)
209
Alla grandezza così definita si dà il nome di “potenza” perché essa è
dimensionalmente omogenea con una potenza. L’aggettivo “virtuale” sta a
indicare che la grandezza definita non ha nessun significato fisico, perché le
intensità di corrente sono del circuito C ′ e le tensioni sono del circuito C ′′ (o
viceversa) e tra esse non intercorre alcuna relazione; l’aggettivo “assorbita” sta
a indicare che il prodotto è tra una tensione e un’intensità di corrente i cui
riferimenti per i versi sono scelti con la convenzione dell’utilizzatore.
+
+
i1′
v ′5
−
i5′
v ′1
+
i4′
+
v ′2
+
i3′ +
i2′
v ′4
v 3′
−
−
(a)
i1′′
v5′′
v1′′
+
i4′′
v4′′
v2′′
i2′′
i3′′
v3′′
i5′′
1
(b)
2
4
5
3
(c)
Fig. 2.45
Un esempio di due circuiti diversi che hanno lo stesso grafo.
Teorema di Tellegen (o teorema della conservazione delle potenze virtuali)
Si considerino due circuiti C ′ e C ′′ che hanno lo stesso grafo orientato. La
somma delle potenze virtuali assorbite (erogate) da ciascun lato del grafo è
uguale a zero, cioè
b
∑ i ′ v ′′ = 0 .
k k
(214)
k =1
♦
La dimostrazione di questa proprietà è diretta conseguenza delle sole leggi di
Kirchhoff ed è simile a quella viene presentata nel precedente paragrafo per
G. Miano, Introduzione ai Circuiti
210
dimostrare la conservazione delle potenze elettriche. La lasciamo al lettore
come esercizio.
È evidente che quando gli elementi dei due circuiti C ′ e C ′′ sono uguali e gli
elementi dinamici hanno le stesse condizioni iniziali, la potenza virtuale
coincide con la potenza elettrica.
Osservazione
L’equazione (214) è di particolare interesse: tra le intensità di corrente
i1′ , i2′ ,...,il′ e le tensioni v1′ ′, v2′ ′,...,vl′′ non sussiste alcuna relazione, se non quella
di fare riferimento allo stesso grafo orientato e soddisfare indipendentemente le
leggi di Kirchhoff. Il teorema di Tellegen discende unicamente dalle leggi di
Kirchhoff. È interessante notare che una delle due leggi di Kirchhoff, unita al
teorema di Tellegen, implica l’altra legge. Si può dimostrare che:
-
-
se per ogni insieme delle tensioni del circuito che verificano le leggi di
Kirchhoff è verificata la conservazione delle potenze virtuali, allora le
intensità di corrente del circuito verificano naturalmente le leggi di
Kirchhoff;
se per ogni insieme delle intensità di corrente del circuito che verificano le
leggi di Kirchhoff è verificata la conservazione delle potenze virtuali,
allora le tensioni del circuito verificano naturalmente le leggi di Kirchhoff.
♦
Se si usa la convenzione del generatore, allora al prodotto tra la tensione e
l’intensità della corrente
Pˆk = ik′ vˆ ′k′ ,
dove vˆ ′k′ = − vk′′ , si dà il nome di potenza virtuale erogata.
G. Miano, Introduzione ai Circuiti
(215)