1. (1-2-2011) Un ragazzo ha mezz’ora per un preparare cocktail prima che arrivi un ospite, ma ha dimenticato il
ghiaccio! Prende 1 litro di acqua a 10 °C e la mette nella vaschetta del ghiaccio nel congelatore, sperando di fare in
tempo. Sapendo che il frigorifero ha un coefficiente di prestazione pari a 5.5, eroga una potenza massima di 550W e
che solo il 10% della potenza elettrica contribuisce al raffreddamento ed al congelamento dell’acqua, stimare se il
ragazzo avrà il ghiaccio in tempo per il suo appuntamento. Si consideri il calore specifico dell’acqua pari a 4.186
kJ/kgK ed il calore latente di fusione/solidificazione del ghiaccio pari a 335.5 kJ/kg.
2. (1-2-2011, 3-10-2011, 18-6-2012, 10-7-2012, 23-7-2013, 3-10-2013) Un ciclo di Carnot viene svolto da una mole di
gas ideale monoatomico tra due isoterme alle quali le energie interne del gas sono, rispettivamente, U1= 3738 J e U2=
4985 J. La variazione di entropia lungo l’isoterma a temperatura maggiore è ΔS2= 3 cal/K. Calcolare il rendimento di
tale ciclo, il lavoro compiuto in esso dal gas e la variazione di entropia ΔS1 lungo l’isoterma a temperature minore.
(NA= 6.02x1023 mole-1, kB=1.38x10-23J/K).
3. (02-03-2011) n = 0.860 moli di gas ideale biatomico occupano il volume VA = 20 · 10−3 m3 alla temperatura TA = 280
K. Con una trasformazione isoterma reversibile il gas viene portato dallo stato A allo stato B con VB = 2.0 · 10−3 m3.
Da B si passa con una trasformazione isobara reversibile a uno stato C tale che con una successiva trasformazione
adiabatica reversibile si possa ritornare allo stato iniziale A. Calcolare: a) la temperatura TC nel punto C; b) il
rendimento del ciclo; c) la variazione di entropia del gas ΔSBC avvenuta nella trasformazione da B a C.
4. (02-03-2011, 3-10-2011, 10-7-2012, 23-7-2013) All'interno di un recipiente completamente isolato e di capacità
termica trascurabile si uniscono le masse M1 = 1000 g di acqua alla temperatura T1 = 80 °C, M2 = 100 g di ghiaccio
fondente (T2 = 0 °C), e M3 = 200 g di ghiaccio a T3 = - 40 °C. Noti i calori specifici di acqua e ghiaccio (che
assumeremo costanti al variare della temperatura) ca = 4200 J/(kgK) e cg = 2200 J/(kgK) rispettivamente, e il calore
latente di fusione L = 333 kJ/kg, calcolare: a) la temperatura finale Tf a cui si porta il sistema all'equilibrio; b) la
quantità di calore complessiva passata dalle componenti del sistema che inizialmente avevano T > Tf a quelle che
avevano T <Tf.
5. (21-06-2011) Un blocco di ghiaccio di massa m1 alla temperatura T1 = -20 °C si trova all’interno di un contenitore
adiabatico. Molto rapidamente vengono immersi nel contenitore un corpo solido di massa m2 = 0.4 kg, calore
specifico c2 = 380 J/kgK, avente temperatura T2 = 60 °C, ed una massa m3 = 0.8 kg di acqua alla temperature T3 = 10
°C. Si osserva che la temperatura di equilibrio è T = -3 °C. Calcolare il valore di m1.
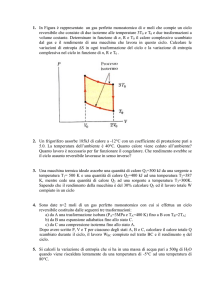
6. (21-06-2011) Tre moli di gas ideale passano dallo stato A (VA=30x10-3 m3, pA=2 bar) allo stato B (VB=100x10-3 m3,
pB=4 bar) compiendo la trasformazione reversibile indicata in figura. Determinare:
a)
se il gas è monoatomico o biatomico sapendo che ΔSAB = 148.2 J/K
b) calcolare il calore scambiato dal gas.
p
B
A
V
7. (19-7-2011) Una quantità di aria a partire dallo stato A definito dalla temperatura TA = 273 K, pressione PA = 1.0 bar
e volume VA = 775 dm3, descrive un ciclo reversibile costituito da: (a) una compressione adiabatica AB a PB = 20.0
bar; (b) una espansione isobara BC durante la quale viene fornita all’aria una quantità di calore Q = 5x105 J; (c) una
espansione adiabatica CD fino a raggiungere il volume VA; (d) una isocora DA fino a raggiungere la pressione
iniziale PA.
Considerando l’aria un gas ideale e biatomico, determinare:
a) la temperatura TB in B;
b) la pressione PD in D;
c) il rendimento η del ciclo;
d) la variazione di entropia ΔSBC dell’aria nella trasformazione BC.
P
B
C
D
A
V
8. (19-7-2011, 18-6-2012) Un secchio ben isolato termicamente, con capacità termica trascurabile, contiene un 150g di
ghiaccio a 0 °C. a) Se nel secchio vengono immessi 20g di vapore a 100 °C, qual è la temperatura finale di
equilibrio del sistema? b) All’equilibrio rimane del ghiaccio? Si consideri il calore latente di fusione del ghiaccio
pari a 333.5 kJ/kg, il calore latente di evaporazione dell’acqua pari a 2257 kJ/kg ed il calore specifico dell’acqua
pari a 4186 J/kg°C.
9. (13-9-2011) Un contenitore è composto da un cilindro cavo di rame di raggio interno pari a 10 cm contiene un
volume di 500 cm3 di glicerina, compresso da un pistone di massa trascurabile spinto da una forza F=1000 N.
Trascurando la dilatazione del rame e supponendo di scaldare il contenitore da T1 = 50 °C a T2 = 150 °C, calcolare:
a) l’aumento di volume della glicerina (coeff. di espansione cubica γ = 5.3x10-4 °C-1)
b) il lavoro meccanico compiuto dalla glicerina espansa contro la forza esterna F
c) la quantità di calore assorbita dalla glicerina assumendone densità ρ = 1.26 gr/cm3 e calore specifico
c = 0.58 cal/g°C costanti.
10. (13-9-2011) Una mole di gas perfetto monoatromico è contenuta in un recipiente non isolato
termicamente a pressione p1, volume V1 e temperatura T1 = 300 K. Successivamente il gas viene
riscaldato fornendogli una quantità di energia E = 8.31 Wh e viene fatto espandere reversibilmente a
pressione costante fino ad un volume V2 a temperatura T2. Calcolare T2 ed il rapporto V2/V1.
11. (12-12-2011, 18-12-2012, 11-12-2013) In un esperimento per trovare il calore specifico, si mescolano
200g di alluminio, a 100 °C con 50 g di acqua a 20°C. Trovare la variazione di entropia del sistema tra lo
stato iniziale e lo stato finale. Calore specifico dell’alluminio cp = 0.215 cal/(g °C), calore specifico
dell’acqua a 20°C ca = 0.998 cal/(g °C).
12. (12-12-2011,11-12-2013) Tre moli di un gas perfetto biatomico, inizialmente a temperatura T0, occupano
un volume V0; esse subiscono una compressione isobara ed il volume passa ad ¼ del valore iniziale.
Successivamente il gas viene riscaldato in modo isocoro fino alla temperatura 3T0. Si calcoli la capacità
termica media del gas relativa alla trasformazione considerata supponendola reversibile.
13. (7-2-2012) Una mole di gas perfetto monoatomico, inizialmente in p1, V1, T1, è sottoposta al ciclo di
figura. Calcolare il lavoro fatto nel ciclo. Ricavare, quindi, un’espressione per il rendimento di un motore
che usi questo processo.
2p1
p1
B
C
A
D
V1
3V1
14. (7-2-2012, 18-12-2012, 4-4-2013) In un cilindro dotato di un pistone mobile a tenuta è contenuto elio gassoso a
310 K. Il gas inizialmente si trova alla pressione di 2 atm (202 kPa) e occupa un volume di 48 litri. Poi subisce
un’espansione isoterma fino a raggiungere il volume di 106 litri, quindi subisce una compressione isobara alla
pressione determinatasi alla fine dell’espansione, tornando così al volume iniziale di 48 litri. Calcolare il lavoro
compiuto dal gas durante (a) l’espansione isoterma, (b) la compressione isobara, (c) l’intero processo. (d) Qual è
la temperatura finale dell’He?
i
202kPa
f
48l
c
106 l
15. (5-3-2012) Un calorimetro in Al (cal. spec. 900 J/kgK) di massa 100 g contiene 250 g di acqua. Il sistema è in
equilibrio a 10 °C. Si immergono nell’acqua due blocchi metallici; uno è costituito da 50 g di rame (cal. spec.
387 J/kgK) a 80 °C, mentre l’altro di massa 70 g si trova inizialmente a 100 °C. L’intero sistema raggiunge la
temperatura di equilibrio 20 °C. Si determini il calore specifico del blocco di materiale sconosciuto.
16. (5-3-2012) Due moli di He gassoso, inizialmente a 300 K e 0.4 atm, subiscono una compressione a temperatura
costante fino a raggiungere la pressione di 1.2 atm. Sotto l’ipotesi di gas perfetto, si trovi: (a) il volume finale del
gas, (b) il lavoro compiuto dal gas, (c) l’energia scambiata sotto forma di calore, (d) la variazione di entropia del
gas.
17. (5-9-2012) La temperatura di 4.34 moli di un gas ideale biatomico viene aumentata di 62,4 K a pressione
costante. Si calcoli:
a) La quantità di calore fornita al gas
b) L’aumento di energia interna del gas
c) L’aumento di energia cinetica traslazionale del gas.
18. (5-9-2012) Una massa d’acqua m = 10 kg a temperatura T1 = 293 K è trasformata in vapore surriscaldato
a temperatura T3 = 523 K a pressione atmosferica costante. Calcolare la variazione di entropia dell’acqua,
sapendo che:
a) Il calore latente di ebollizione è λeb= 22.6x105 J/kg
b) Il calore di vaporizzazione è λev = (1670 + 0.494T + 1.86x106 T-2) J/(kg K)
19. (30-01-2013) Il calore specifico a pressione costante cp per molte sostanze può essere espresso con buona
approssimazione dalla relazione empirica cp = (a + bT), con “a” e “b” costanti dipendenti dal materiale e “T”
temperatura assoluta.
a) Calcolare la quantità di calore assorbita e la variazione di entropia di una massa riscaldata da T1 a T2.
b) Calcolare ΔS per una mole di rame quando la sua temperatura viene portata a p = cost. da T1 = 300 K a T2 =
1200 K, sapendo che a = 2.3x104 J/moleK e b = 5.92 J/moleK2.
20. (30-01-2013) Calcolare il rendimento di un ciclo reversibile di Clausius-Clapeyron svolto da un gas perfetto
biatomico rappresentato nel piano pV dalle seguenti trasformazioni: AB e CD isobare, BC e DA isocore. Si
considerino pA = pB = 3atm; pC = pD = 1atm; VB = VC = 5 litri; VA = VD = 1 litro.
21. (27-2-2013) Per misurare il calore specifico del Pb (piombo) si riscaldano 600 g di Pb fino alla temperatura di
100 °C e li si pongono in un calorimetro di Al (alluminio) con massa di 200 g che contiene 500 g d’acqua,
inizialmente alla temperatura di 17.3 °C. Se la temperatura finale della miscela vale 20 °C, qual è il calore
specifico del Pb? Il calore specifico dell’Al vale 0.900 kJ/(kg K).
22. (27-2-2013) Un sistema formato da 0.32 moli di gas perfetto monoatomico occupa un volume di 2.2 L alla
pressione di 2.4 atm(punto A in figura). Al sistema viene fatto compiere un ciclo costituito dalle seguenti 3
trasformazioni:
a) Il gas è riscaldato a pressione costante fino a raggiungere un volume pari a 4.4 L (punto B).
b) Il gas è raffreddato a volume costante fino a raggiungere una pressione pari a 1.2 atm
(punto C).
c) Il gas è sottoposto ad una compressione isoterma che lo fa tornare nel punto A.
Qual è la temperatura nei punti A, B e C? Determinare il lavoro W, il calore scambiato Q e la
variazione di energia interna ΔU per ciascuna trasformazione e per l’intero ciclo.
P
A
B
C
V
23. (4-4-2013) Si consideri un sistema formato da acqua divisa in due parti: 0.3 kg inizialmente a T 90 °C e 0.7kg
inizialmente a 10 °C. Supponiamo che le due quantità d’acqua vengano mescolate in un recipiente isolato
termicamente e raggiungano l’equilibrio. Determinare la variazione di entropia dell’intero sistema di 1 kg di
acqua.
24. (3-10-2013) In un calorimetro di massa trascurabile si miscelino M1 = 100 g di acqua alla temperatura T1
= 60 °C, M2 = 40 g di ghiaccio fondente (temperatura T2 = 0 °C), e M3 = 20 g di ghiaccio a T3 = - 20 °C.
Noti i calori specifici di acqua e ghiaccio (che assumeremo costanti) ca = 4200 J/(kgK) e cg = 2200
J/(kgK) rispettivamente, e il calore latente di fusione L = 333 kJ/kg, calcolare la temperatura finale Tf a
cui si porta il sistema all'equilibrio.