LE LEGGI DEI GAS
Dalle prime teorie cinetiche dei gas
simulazioni della dinamica molecolare.
Lezioni d'Autore
alle
Un video :
Clic
Un altro video :
Clic
Un altro video (in inglese):
Clic
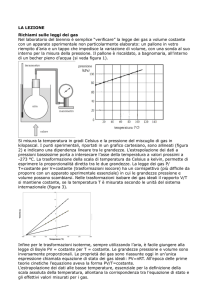
Richiami sulle leggi dei gas (I)
E' semplice “verificare” la
legge dei gas a volume
costante con un apparato
sperimentale non
particolarmente elaborato:
un pallone in vetro
riempito d’aria e un tappo
che impedisce la variazione
di volume, con una sonda
al suo interno per la misura
della pressione. Il pallone è
riscaldato, a bagnomaria,
all’interno di un becher
pieno d’acqua.
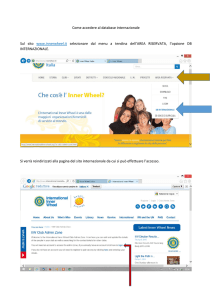
Richiami sulle leggi dei gas (II)
Si misura la
temperatura in
gradi Celsius e la
pressione del
miscuglio di gas
in kilopascal. I
punti
sperimentali,
riportati in un
grafico
cartesiano, sono
allineati e
indicano una
dipendenza
lineare tra le
grandezze.
Richiami sulle leggi dei gas (III)
L’estrapolazione dei
dati a pressioni
bassissime porta a
intersecare l’asse
della temperatura a
valori prossimi a
-273 °C. La
trasformazione
della scala di
temperatura da
Celsius a kelvin,
permette di
esprimere la
proporzionalità
diretta tra le due
grandezze.
Richiami sulle leggi dei gas (IV)
La legge dei gas P/T=costante per
V=costante (trasformazioni isocore) ha un
corrispettivo (più difficile da proporre con un
apparato sperimentale essenziale) in cui le
grandezze pressione e volume possono
scambiarsi.
Richiami sulle leggi dei gas (V)
Nelle trasformazioni isobare dei gas ideali il
rapporto V/T si mantiene costante, se la
temperatura T è misurata secondo le unità di
misura del Sistema Internazionale.
Richiami sulle leggi dei gas (VI)
Infine per le trasformazioni isoterme, sempre
utilizzando l’aria, è facile giungere alla legge di
Boyle:
PV = costante per T = costante.
Le grandezze pressione e volume sono perciò
inversamente proporzionali fra loro.
Le proprietà dei gas sono riassunte oggi in
un’unica espressione chiamata equazione di stato
dei gas ideali: PV=nRT.
All’epoca delle prime teorie cinetiche l’equazione
aveva la forma PV/T=costante.
Richiami sulle leggi dei gas
(VII)
Nella forma moderna dell’equazione di stato è
implicito, tramite la quantità di sostanza n (il
numero di moli), un legame tra grandezze
macroscopiche e mondo microscopico. Infatti per
il calcolo della quantità di sostanza bisogna
conoscere l’espressione chimica della molecola
(concetto non ancora ben distinto da atomo per i
chimici del 1860) e la massa della sostanza.
Un primo modello cinetico (I)
Dai corpuscola motu rapidissimo e dalla vis viva
di Daniel Bernoulli del 1738 ai primi lavori di
Clausius e Maxwell sui gas (circa 1860) intercorre
un periodo complesso in cui articoli con
riferimenti cinetici ai gas di alcuni autori furono
rifiutati per i pareri negativi dei referenti
scientifici, mentre i chimici ancora dibattevano
sulla nomenclatura e i concetti di atomi e
molecole. Solo con il delinearsi del primo principio
della termodinamica (il principio di conservazione
dell’energia) le ricerche “sul moto che noi
chiamiamo calore” trovarono rinnovato vigore.
Un primo modello cinetico (II)
Un modello 'zero'
costituito da N
corpuscoli, di uguale
massa m, così piccoli da
non interagire (punti
materiali) che urtano
elasticamente le pareti
di un recipiente, porta a
un’energia complessiva
E uguale alla somma
delle energie cinetiche
delle particelle che,
secondo le ipotesi, si
conserva.
Un primo modello cinetico (III)
L’energia media ε di un singolo corpuscolo
è allora E/N, mentre il modulo della
velocità n (rappresentativa dell’insieme)
coincide allora, uguagliando le energie
cinetiche, con la velocità quadratica
media:
Un primo modello cinetico (IV)
Utilizzando il teorema dell’impulso per ogni
componente di questa velocità si può scrivere:
Infine dall’equazione di stato dei gas segue
l’uguaglianza:
ovvero:
Un primo modello cinetico (V)
Non solo la pressione è conseguenza dell’urto
incessante delle molecole di gas sulle pareti
del recipiente, ma la temperatura assoluta è
correlata strettamente alle velocità delle
particelle (energia e velocità sono funzioni
crescenti della temperatura stessa).
La conclusione è ovvia se si analizza la
definizione di gas ideale, l’energia interna può
dipendere solo dalla temperatura assoluta.
L’energia del modello di particelle non
interagenti (con urti contro le pareti
perfettamente elastici) presuppone solo
un’energia cinetica. Quindi la temperatura
assoluta è funzione solo della velocità
quadratica media.
Verso un nuovo modello cinetico dei gas (I)
Vediamo le critiche storiche e il possibile
perfezionamento del modello 'zero'.
Una premessa sperimentale...
Un’esperienza molto citata di diffusione dei gas
è quella dei vapori di bromo in aria,
semplicemente per la sua visibilità. Se si
collega un cilindro, inizialmente pieno solo
d’aria, con un recipiente pieno di vapori di
bromo (di colore giallo marrone) l’interno del
cilindro assume gradualmente tonalità più
scure.
Verso un nuovo modello cinetico dei gas (II)
Il processo si completa, a temperatura
ambiente, in circa un’ora. Tutto ciò fa pensare
a una bassa velocità delle molecole del gas. Ma
ciò non si concilia facilmente con la velocità
campione v calcolabile dalla teoria cinetica.
Verso un nuovo modello cinetico dei gas (III)
Il primo autore che effettuò una valutazione di
una simile velocità fu Clausius che ottenne alla
temperatura di 0 °C e alla pressione di 1
atmosfera per l’ossigeno 461 m/s, per l’azoto
494 m/s e per l’idrogeno 1844 m/s.
Valori apparentemente inconciliabili con la
lenta diffusione dei gas. Solo approfondendo il
modello cinetico è possibile trovare una
spiegazione a un simile comportamento
perché, come abbiamo già ricordato, il modello
zero cinetico non considera le interazioni tra i
punti materiali.
Verso un nuovo modello cinetico dei gas (IV)
Come si può tenere conto delle collisioni tra i
corpuscoli? La risposta di Clausius si avvalse di
nuovi concetti (oggi parliamo di cammino
libero medio e di sezione d’urto). Il suo
modello cinetico non modifica le proprietà di
equilibrio dei gas (energia interna, equazione
di stato) ma è necessario per spiegare
microscopicamente fenomeni dinamici quali la
viscosità, la conduzione termica e la diffusione.
I punti materiali, per tenere conto delle
collisioni, sono sostituiti da sferette con raggio
d’azione r, all’interno delle quali agiscono forze
repulsive.
Verso un nuovo modello cinetico dei gas (V)
Gli urti
conseguenti
trasformano il
moto rettilineo dei
corpuscoli in un
percorso a zig
zag. La distanza
media tra due urti
successivi è
chiamato
cammino libero
medio. La
distanza d relativa
a un urto elastico
(contatto tra due
particelle) è
uguale a 2r.
Verso un nuovo modello cinetico dei gas (VI)
La superficie della singola sfera, pari a
4pr2=pd2, è invece la sezione d’urto, misura
della probabilità di deflessione di una
particella.
Se il percorso è frastagliato e irregolare, per
l’elevatissimo numero delle collisioni, le
particelle si mantengono a lungo in un volume
limitato anche con velocità elevate. Ovvero se
il valore del cammino libero medio è piccolo, il
gas mostra complessivamente una diffusione
lenta. Il modello delle sfere d’azione permette
una prima stima delle dimensioni atomiche e
del numero di molecole contenute in una mole
di gas.
Cenni sulle simulazioni della dinamica
molecolare (I)
Consideriamo ancora un modello di gas in
cui si possa trascurare la struttura delle
molecole composto da N molecole
sferiche interagenti a coppie secondo una
forza F(r) funzione nota della distanza r
(per le capacità di calcolo degli elaboratori
N non potrà essere molto grande). Si
fissano le posizioni r(0) e le velocità
iniziali v(0) delle particelle e si effettua la
somma vettoriale delle forze agenti sulle
molecole.
Cenni sulle simulazioni della dinamica
molecolare (II)
Dal secondo principio principio della
dinamica si ricavano le accelerazioni. Le
variazioni di velocità dipendono da un
arbitrario intervallo di tempo Dt (piccolo
rispetto alla durata della simulazione,
grande rispetto ai tempi caratteristici
associati alle interazioni molecolari).
Fissato Dt si calcola Dv=a Dt. Quindi le
nuove velocità diventano v(Dt)=v(0)+ D v
e le nuove coordinate r = r(0) + v Dt.
Cenni sulle simulazioni della dinamica
molecolare (III)
A questo punto si itera il procedimento su
tempi lunghi rispetto al tempo Dt. In realtà il
calcolo numerico (la scelta dell’algoritmo) è
assai varia: A esempio le posizioni e le
velocità possono essere determinate per un
tempo Dt/2, oppure si possono adottare altri
metodi di correzione.
Cenni sulle simulazioni della dinamica
molecolare (IV)
La difficoltà principale della simulazione
consiste nel calcolo delle forze. Infine per
ritornare alle considerazioni cinetiche le
quantità termodinamiche sono dedotte dalla
solita relazione:
dove con k si è indicata la costante di
Boltzmann (il rapporto tra la costante R dei
gas e il numero di Avogadro N).
Cenni sulle simulazioni della dinamica
molecolare (V)
Si assume dunque valido il principio di
equipartizione che associa a ogni grado di
libertà della particella (in questo caso le
tre componenti della velocità) un’energia
pari a:
Altri video:
Video.1 Idee della chimica: le leggi dei gas Clic
Video.2 Teoria cinetica del gas prima parte (calore
come moto casuale di atomi e molecole) Clic
Video.3 Teoria cinetico molecolare Il filmato mostra come
la diffusione dell’inchiostro in un liquido caldo avvenga più rapidamente
dello stesso fenomeno in un liquido freddo.
Clic
Video.4 Calore e temperatura Clic
Video.5 Introduzione alla teoria cinetica dei gas
(in inglese) Clic