LA LEZIONE
Richiami sulle leggi dei gas
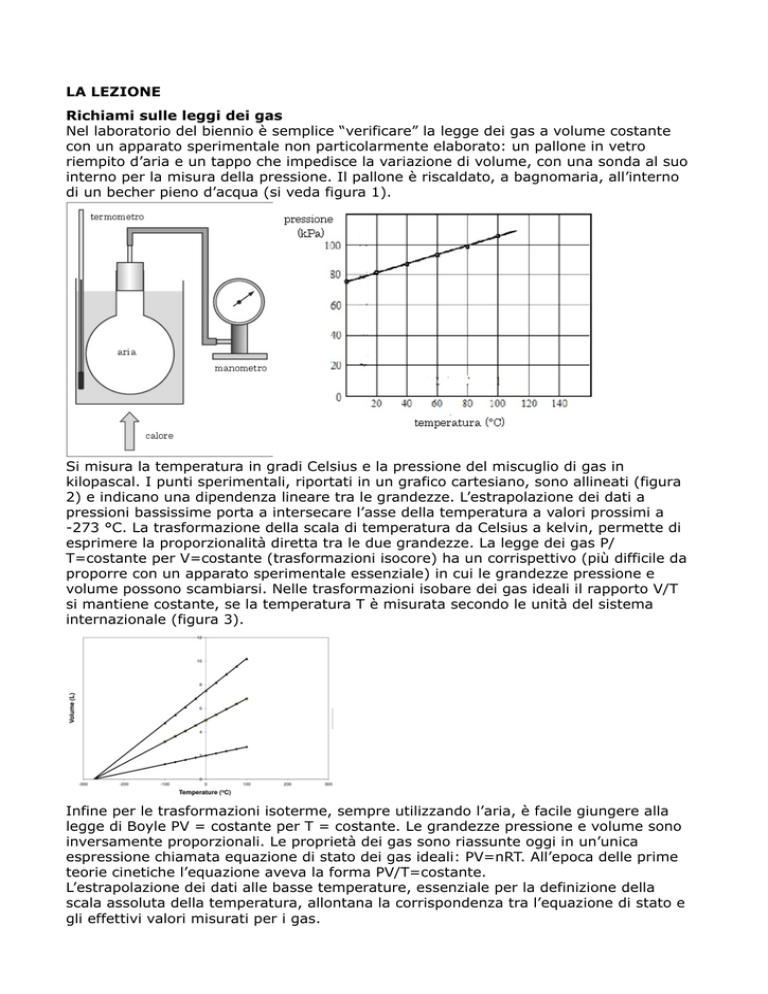
Nel laboratorio del biennio è semplice “verificare” la legge dei gas a volume costante
con un apparato sperimentale non particolarmente elaborato: un pallone in vetro
riempito d’aria e un tappo che impedisce la variazione di volume, con una sonda al suo
interno per la misura della pressione. Il pallone è riscaldato, a bagnomaria, all’interno
di un becher pieno d’acqua (si veda figura 1).
Si misura la temperatura in gradi Celsius e la pressione del miscuglio di gas in
kilopascal. I punti sperimentali, riportati in un grafico cartesiano, sono allineati (figura
2) e indicano una dipendenza lineare tra le grandezze. L’estrapolazione dei dati a
pressioni bassissime porta a intersecare l’asse della temperatura a valori prossimi a
-273 °C. La trasformazione della scala di temperatura da Celsius a kelvin, permette di
esprimere la proporzionalità diretta tra le due grandezze. La legge dei gas P/
T=costante per V=costante (trasformazioni isocore) ha un corrispettivo (più difficile da
proporre con un apparato sperimentale essenziale) in cui le grandezze pressione e
volume possono scambiarsi. Nelle trasformazioni isobare dei gas ideali il rapporto V/T
si mantiene costante, se la temperatura T è misurata secondo le unità del sistema
internazionale (figura 3).
Infine per le trasformazioni isoterme, sempre utilizzando l’aria, è facile giungere alla
legge di Boyle PV = costante per T = costante. Le grandezze pressione e volume sono
inversamente proporzionali. Le proprietà dei gas sono riassunte oggi in un’unica
espressione chiamata equazione di stato dei gas ideali: PV=nRT. All’epoca delle prime
teorie cinetiche l’equazione aveva la forma PV/T=costante.
L’estrapolazione dei dati alle basse temperature, essenziale per la definizione della
scala assoluta della temperatura, allontana la corrispondenza tra l’equazione di stato e
gli effettivi valori misurati per i gas.
Nella forma moderna dell’equazione di stato è implicito, tramite la quantità di sostanza
n (il numero di moli), un legame tra grandezze macroscopiche e mondo microscopico.
Infatti per il calcolo della quantità di sostanza bisogna conoscere l’espressione chimica
della molecola (concetto non ancora ben distinto da atomo per i chimici del 1860) e la
massa della sostanza. Inoltre, nelle stesse condizioni di pressione e temperatura,
volumi uguali contengono la stessa quantità di gas espressa in moli.1 Ciò permette di
dare una duplice interpretazione alle reazioni chimiche riguardanti il gas. Consideriamo
a esempio la reazione tra idrogeno e ossigeno con la produzione di vapor acqueo. Dal
punto di vista microscopico due molecole di ossigeno reagiscono con una molecola di
ossigeno per produrre due molecole di acqua. Dal punto di vista macroscopico 2 volumi
di idrogeno reagiscono con 1 volume di ossigeno per dare luogo a 2 volumi di vapor
acqueo 2. Il numero di entità elementari contenute in una mole di una sostanza è oggi
conosciuto come costante o numero di Avogadro.
Un primo modello cinetico
Dai corpuscola motu rapidissimo e dalla vis viva di Daniel Bernoulli del 1738 ai primi
lavori di Clausius 3 e Maxwell sui gas (circa 1860) intercorre un periodo complesso in cui
articoli con riferimenti cinetici ai gas di alcuni autori4 furono rifiutati per i pareri
negativi dei referenti scientifici, mentre i chimici ancora dibattevano sulla nomenclatura
e i concetti di atomi e molecole. Solo con il delinearsi del primo principio della
termodinamica (il principio di conservazione dell’energia) le ricerche “sul moto che noi
chiamiamo calore” trovarono rinnovato vigore. Oggi è chiaro. Un modello zero
(si veda figura), costituito da N corpuscoli, di uguale massa m, così piccoli da non
interagire (punti materiali) che urtano elasticamente le pareti di un recipiente, porta a
1 Amedeo Avogadro fu il primo a proporre questo passaggio. In mancanza del concetto di mole, l’autore
parlava di molecole.
2 L’esperienza con il voltametro di Hofmann in cui idrogeno e ossigeno sono formati a partire dall’acqua
non è nel repertorio del laboratorio di fisica (è considerata troppo chimica). Eppure, nel caso di presenza
dell’apparato, dovrebbe costituire una delle esperienze dimostrative del biennio liceale.
3 La versione inglese di articoli di teoria cinetica è stata curata da Stephen G. Brush nel 1965. Un lungo
lavoro tratto dalla collezione è The nature of the motion which we call heat, Clausius, 1857. La versione
digitale è reperibile all’indirizzo: http://www.ffn.ub.es/luisnavarro/nuevo_maletin/Clausius%20(1857)
_Nature%20motion%20we%20call%20heat.pdf
4 John Herapath nel 1820 e John James Waterston nel 1846 presentarono alla Royal Society articoli che
non furono pubblicati. In essi gli autori elaboravano modelli cinetici di gas come insieme di corpuscoli
interagenti per collisione. Il punto di partenza era dimostrare come l’insieme potesse dar luogo a effetti
gravitazionali. Al proposito si rimanda a Dal calorico alla conservazione dell’energia di Enrico Bellone,
volume terzo di Storia della scienza a cura di Paolo Rossi, Gruppo editoriale l’Espresso, 2006.
un’energia complessiva E uguale alla somma delle energie cinetiche delle particelle che,
secondo le ipotesi, si conserva. L’energia media ε di un singolo corpuscolo è allora E/N,
mentre il modulo della velocità v (rappresentativa dell’insieme) coincide allora,
uguagliando le energie cinetiche, con la velocità quadratica media:
v=
v12 + v2 2 + v32 + ...+ vN 2
N
Utilizzando il teorema dell’impulso per ogni componente di questa velocità si può
scrivere:
PV = Nmvx 2 =
1
Nmv 2 , con vx 2 + vy 2 + vz 2 = v 2 .
3
Infine dall’equazione di stato dei gas segue l’uguaglianza
E=
nRT =
2
N ε , ovvero:
3
3
nRT .
2
Non solo la pressione è conseguenza dell’urto incessante delle molecole di gas sulle
pareti del recipiente, ma la temperatura assoluta è correlata strettamente alle velocità
delle particelle (energia e velocità sono funzioni crescenti della temperatura stessa). La
conclusione è ovvia se si analizza la definizione di gas ideale, l’energia interna può
dipendere solo dalla temperatura assoluta. L’energia del modello di particelle non
interagenti (con urti contro le pareti perfettamente elastici) presuppone solo un’energia
cinetica. Quindi la temperatura assoluta è funzione solo della velocità quadratica
media. Vediamo le critiche storiche e il possibile perfezionamento del modello.
Verso un nuovo modello cinetico dei gas
Un’esperienza molto citata di diffusione dei gas è quella dei vapori di bromo in aria,
semplicemente per la sua visibilità. Se si collega un cilindro, inizialmente pieno solo
d’aria, con un recipiente pieno di vapori di bromo (di colore giallo marrone) l’interno del
cilindro assume gradualmente tonalità più scure. Il processo si completa, a
temperatura ambiente, in circa un’ora (figura 5).
Tutto ciò fa pensare a una bassa velocità delle molecole del gas. Ma ciò non si concilia
facilmente con la velocità campione v calcolabile dalla teoria cinetica. Il primo autore
che effettuò una valutazione di una simile velocità fu Clausius che ottenne alla
temperatura di 0 °C e alla pressione di 1 atmosfera per l’ossigeno 461 m/s, per l’azoto
494 m/s e per l’idrogeno 1844 m/s.
Valori apparentemente inconciliabili con la lenta diffusione dei gas. Solo approfondendo
il modello cinetico è possibile trovare una spiegazione a un simile comportamento
perché, come abbiamo già ricordato, il modello zero cinetico non considera le
interazioni tra i punti materiali. Come si può tenere conto delle collisioni tra i
corpuscoli? La risposta di Clausius si avvalse di nuovi concetti (oggi parliamo di
cammino libero medio e di sezione d’urto). Il suo modello cinetico non modifica le
proprietà di equilibrio dei gas (energia interna, equazione di stato) ma è necessario per
spiegare microscopicamente fenomeni dinamici quali la viscosità, la conduzione termica
e la diffusione. I punti materiali, per tenere conto delle collisioni, sono sostituiti da
sferette con raggio d’azione r, all’interno delle quali agiscono forze repulsive. Gli urti
conseguenti trasformano il moto rettilineo dei corpuscoli in un percorso a zig e zag. La
distanza media tra due urti successivi è chiamato cammino libero medio. La distanza d
relativa a un urto elastico (contatto tra due particelle) è uguale a 2r (figura 6).
La superficie della singola sfera, pari a 4πr2=πd2, è invece la sezione d’urto, misura
della probabilità di deflessione di una particella.
Se il percorso è frastagliato e irregolare, per l’elevatissimo numero delle collisioni, le
particelle si mantengono a lungo in un volume limitato anche con velocità elevate.
Ovvero se il valore del cammino libero medio è piccolo, il gas mostra
complessivamente una diffusione lenta. Il modello delle sfere d’azione permette una
prima stima delle dimensioni atomiche e del numero di molecole contenute in una mole
di gas.5
Inoltre i discorsi probabilistici possono essere sviluppati per arrivare alla distribuzione
delle velocità delle particelle a una determinata temperatura. Percorso intrapreso da
Maxwell nel 1860.6
Ma qui vorremmo rimandare ulteriori considerazioni statistiche e passare ad affrontare
gli urti tra particelle in accordo al paradigma newtoniano e alle moderne tecnologie dei
calcolatori.
Cenni sulle simulazioni della dinamica molecolare
Consideriamo ancora un modello di gas in cui si possa trascurare la struttura delle
molecole composto da N molecole sferiche interagenti a coppie secondo una forza F(r)
funzione nota della distanza r (per le capacità di calcolo degli elaboratori N non potrà
essere molto grande). Si fissano le posizioni r(0) e le velocità iniziali v(0) delle
particelle e si effettua la somma vettoriale delle forze agenti sulle molecole. Dal
secondo principio principio della dinamica si ricavano le accelerazioni. Le variazioni di
velocità dipendono da un arbitrario intervallo di tempo Δt (piccolo rispetto alla durata
della simulazione, grande rispetto ai tempi caratteristici associati alle interazioni
molecolari). Fissato Δt si calcola Δv=a Δt. Quindi le nuove velocità diventano v(Δt)=v
(0)+ Δ v e le nuove coordinate r = r(0) + v Δt. A questo punto si itera il procedimento
su tempi lunghi rispetto al tempo Δt. In realtà il calcolo numerico (la scelta
dell’algoritmo) è assai varia: A esempio le posizioni e le velocità possono essere
5 Loschmidt ( "Zur Grösse der Luftmoleküle". Sitzungsberichte der kaiserlichen Akademie der
Wissenschaften Wien 52, 395-413, 1865) fu il primo, a partire dai lavori di Clausius, che sviluppò
considerazioni al riguardo anche se non dedusse esplicitamente il valore oggi noto anche come costante di
Loschmidt P0/k T0 (k costante di Boltzmann) che esprime il numero di particelle di un gas ideale contenuto
in un volume di riferimento fissato dalla pressione standard P0= 1 atm e alla temperatura T0= 0° C. Al
proposito si rimanda alla versione inglese in http://www.chemteam.info/Chem-History/
Loschmidt-1865.html
6 James Clerk Maxwell, Illustrations of the dynamical theory of gases, in http://hermes.ffn.ub.es/
luisnavarro/nuevo_maletin/Maxwell_1860_Equilibrium_distribution.pdf
determinate per un tempo Δt/2, oppure si possono adottare altri metodi di correzione.
La difficoltà principale della simulazione consiste nel calcolo delle forze. Infine per
ritornare alle considerazioni cinetiche le quantità termodinamiche sono dedotte dalla
solita relazione:
E=
3
3
nRT = NkT , dove con k si è indicata la costante di
2
2
Boltzmann (il rapporto tra la costante R dei gas e il numero di Avogadro NA).
Si assume dunque valido il principio di equipartizione che associa a ogni grado di libertà
della particella (in questo caso le tre componenti della velocità) un’energia pari a
1
kT .
2












