Fisica Page 1
Sistemi di particelle, forze interne ed esterne.
SISTEMI DI PARTICELLE (PUNTI MATERIALI)
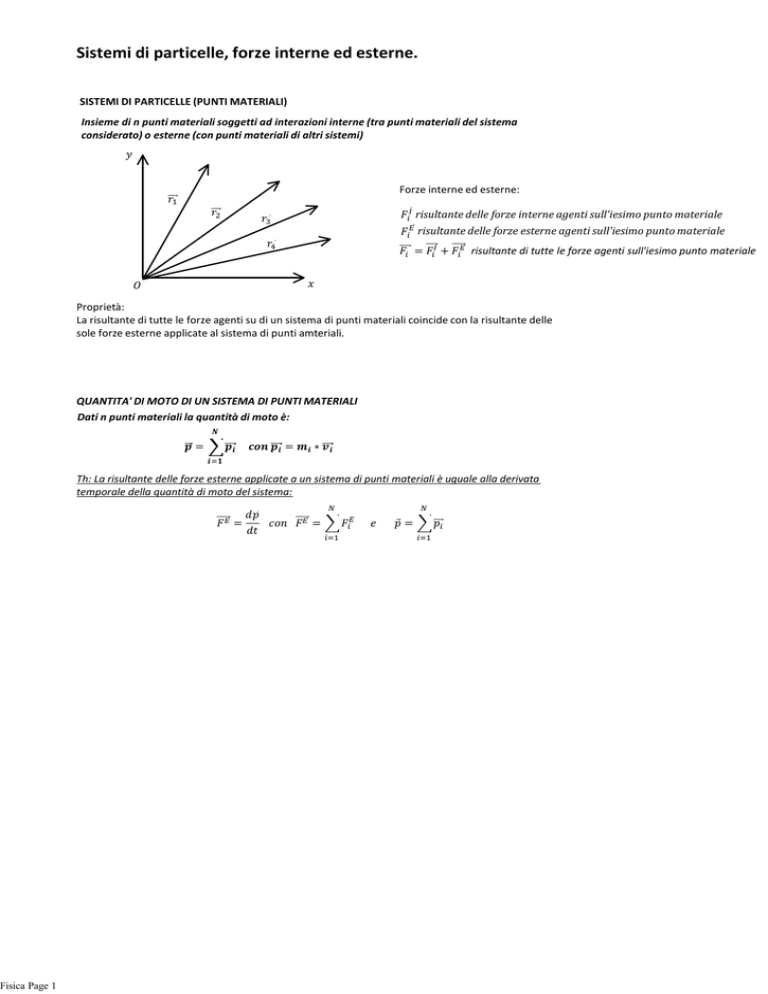
Insieme di n punti materiali soggetti ad interazioni interne (tra punti materiali del sistema
considerato) o esterne (con punti materiali di altri sistemi)
Forze interne ed esterne:
risultante delle forze interne agenti sull'iesimo punto materiale
risultante delle forze esterne agenti sull'iesimo punto materiale
risultante di tutte le forze agenti sull'iesimo punto materiale
Proprietà:
La risultante di tutte le forze agenti su di un sistema di punti materiali coincide con la risultante delle
sole forze esterne applicate al sistema di punti amteriali.
QUANTITA' DI MOTO DI UN SISTEMA DI PUNTI MATERIALI
Dati n punti materiali la quantità di moto è:
Th: La risultante delle forze esterne applicate a un sistema di punti materiali è uguale alla derivata
temporale della quantità di moto del sistema:
Fisica Page 1
Prima equazione cardinale della dinamica dei sistemi,
conservazione della quantità di moto.
La prima equazione cardinale descrive il moto traslatorio di un sistema. Un risultato importante dal
punto di vista intuitivo è che il centro di massa si muove come un punto materiale di massa M pari alla
massa totale del sistema e soggetto a una forza uguale alla risultante delle forze esterne agenti. Essa
prende la forma:
Th di conservazione della quantità di moto:
In un sistema di punti materiali non soggetti ad interazioni con l'esterno , la quantità di moto del sistema si conserva
Anche se
può accadere che
infinitesimo. Infatti:
sia
cioè che
sia costante, ma solo per un intervallo di tempo
Fisica Page 1
Centro di massa e teorema del moto del centro di massa.
CENTRO DI MASSA
Il centro di massa di un sistema di punti materiali
è un punto dello spazio individuato dal vettore
posizione
La
non è altro che la media pesata delle posizioni dei punti materiali del sistema con i pesi
proporzionali alle rispettive masse
Th del centro di massa:
Il CM di un sistema di punti materiali si muove come un punto materiale di massa pari alla massa totale
del sistema soggetto alla risultante di tutte le forze esterne agenti sul sistema
Dimostrazione:
Derivo ambo i membri rispetto al tempo:
Dato che:
Derivo ancora rispetto al tempo
Per un sistema non soggetto a forze esterne
trovo:
Anche se in generale tutte le
non saranno costanti nel tempo.
Fisica Page 1
Energia cinetica di un sistema, teorema di König.
-SISTEMA TRASPOSTO (PER DUE PUNTI MATERIALI)-
Sistema assoluto
Sistema relativo
MOMENTO RISULTANTE DELLE FORZE AGENTI SU UN SISTEMA DI PUNTI MATERIALI
Momento
risultante delle
sole forze esterne
Momento
risultante delle
sole forze interne
Th: 1° teorema di König
Il momento angolare di un sistema di punti materiali rispetto ad un polo O fisso in un SdR inerziale è
legato al momento angolare rispetto al suo centro di massa dalla seguente relazione:
Sistema di riferimento C (del CM in moto
puramente traslazionale)
Fisica Page 2
ENERGIA CINETICA DI UN SISTEMA DI PUNTI MATERIALI
Th: 2° Teorema di König
L'energia cinetica di un sistema di punti materiali in un SdR inerziale (assoluto) è legata all'energia
cinetica nel SdR C (del centro di massa, sistema relativo) dalla relazione seguente:
Dimostrazione
Essendo
e
per il sistema C così come l'abbiamo) definito
Il centro di massa è un ente sintetico del comportamento di un sistema di punti materiali non
esaustivi:
Fisica Page 1
Teorema dell'energia cinetica e conservazione dell'energia per i
sistemi di particelle.
Th dell'energia cinetica (o delle forze vive) per un sistema di punti materiali.
Se un sistema di punti materiali passa dallo stato A (individuato dalle sue coordinate) allo stato B, il lavoro compiuto dalla
risultante di tutte le forze applicate al sistema (interne ed esterne) è pari alla variazione di energia cinetica tra A e B.
Dimostrazione
Sommando sull'indice i da 1 a n
ENERGIA POTENZIALE INTERNA (DELLE FORZE INTERNE)
Se le forze interne ad un sistema di punti materiali sono conservative definiremo energia potenziale
interna l'indice di stato fisico:
Consideriamo un sistema di punti materiali interagenti tra di loro (attraverso forze interne) e con
l'esterno (attraverso forze esterne)
Se
è conservativo potrò introdurre un'energia potenziale interna
Per un sistema di n punti materiali posso ripetere i medesimi argomenti a ciascuna coppia del
sistema
Quindi associare a
la differenza
Sistema di punti materiali rigidi (corpi rigidi)
ENERGIA PROPRIA DI UN SISTEMA DI PUNTI MATERIALI
è propria perchè non dipende esplicitamente dalle forze esterne.
Fisica Page 2
è propria perchè non dipende esplicitamente dalle forze esterne.
In realtà dipende fisicamente espli citamente dalle forze esterne attraverso
Se anche le forze esterne sono conservative allora:
ENERGIA MECCANICA DEL SISTEMA
Th di conservazione dell'energia meccanica
In un sistema di punti materiali soggetto unicamente a forze conservative l'energia meccanica è una
costante del moto (si conserva)
Dimostrazione:
Abbiamo visto che
Se ora diciamo che
cioè che le forze esterne sono conservative allora:
ENERGIA INTERNA DI UN SISTEMA DI PUNTI MATERIALI
Fisica Page 1
Seconda equazione cardinale della dinamica dei sistemi.
Conservazione del momento angolare.
-MOMENTO ANGOLARE DI UN SISTEMA DI PUNTI MATERIALI-
Con
momento angolare dell'iesimo punto materiale rispetto a . In questo caso
è il momento angolare NON il lavoro
Th: 2° equazione cardinale della dinamica dei sistemi:
La derivata temporale del momento angolare del sistema dei punti materiali rispetto a un sistema di polo
risultante dei momenti agenti sul sistema spemre agenti nello stess polo:
Dimostrazione:
Consideriamo l'iesimo punto materiale, per esso vale la 2° equazione cardinale del punto materiale
. Sommando sull'indice i da 1 a n ambo i membri:
Sistema isolato quando:
Quindi un sistema isolato conserva sia la quantità di moto che il momento angolare
Th conservazione del momento angolare
In un SdR inerziale un sistema di punti materiali non soggetto a momenti di forze esterni
moemento angolare si conserva.
2° EQUAZIONE CARDINALE RISPETTO A D UN POLO MOBILE
SdR inerziale (sistema assoluto)
Sommando sull'indice n ho:
il
è uguale alla
Fisica Page 2
Riassumendo:
I equazione
II equazione
Per il caso di n punti materiali a parte il diverso (in generale) significato di
che:
e di
si ha in particolare
Fisica Page 1
Impulso di una forza e teorema dell'impulso.
Con il termine impulso si indica il cambiamento di quantità di moto di un determinato corpo in un
intervallo di tempo . L'introduzione del concetto di impulso permette di enunciare il teorema
dell'impulso, utilizzato in particolare nel campo degli urti, della diffusione e per lo studio delle forze
impulsive. Grazie alla legge di conservazione della quantità di moto si può dedurre che in un sistema
isolato l'impulso totale è nullo.
Th dell'impulso
l'impulso di una forza è uguale alla variazione della quantità di mot del sistema su cui essa agisce
Dimostrazione
Fisica Page 1
Fenomeni d'urto.
URTO TRA PUNTI MATERIALI
È un interazione molto breve e molto intensa tra punti materiali (particelle)
Si distinguono fenomenologicamente tre fasi in un moto:
1. Moto indipendente iniziale delle particelle urtanti (interazione di urto non ancora presente, in
pratica è trascurabile);
2. Interazione vera e propria (contatto più deformazione e rilascio della deformazione);
3. Moto indipendente finale delle particelle urtanti.
La fase 2 dura un (intervallo di tempo) molto breve durante il quale si sviluppano interazioni interne
forti tipicamente impulsive
Impulso agente sull'iesimo punto materiale (dovuto alla
risultante delle forze interne agenti sull'iesimo punto
materiale)
Per il Th dell'impulso per un singolo punto materiale si avrà:
Quindi l'iesimo punto materiale modifica la sua quantità di moto
in ragione dell'impulso
Ruolo delle forze esterne:
In generale durante l'urto i punti materiali urtanti non sono isolati. Tuttavia se le forze esterne non
hanno natura impulsiva esse non possono modificare la quantità di moto dei punti materiali in un
molto piccolo (idealmente
).
Classificazione di moti:
• Perfettamente elastici:
conservano l'energia cinetica del sistema;
• Anelastici:
una parte dell'energia cinetica iniziale viene dissipata
○ Perfettamente anelastici:
cioè
;
• Superelastici:
conversione di energia non meccanica in energia cinetica.












