B
A
S
I
S
P
E
R
I
M
E
N
T
A
L
I
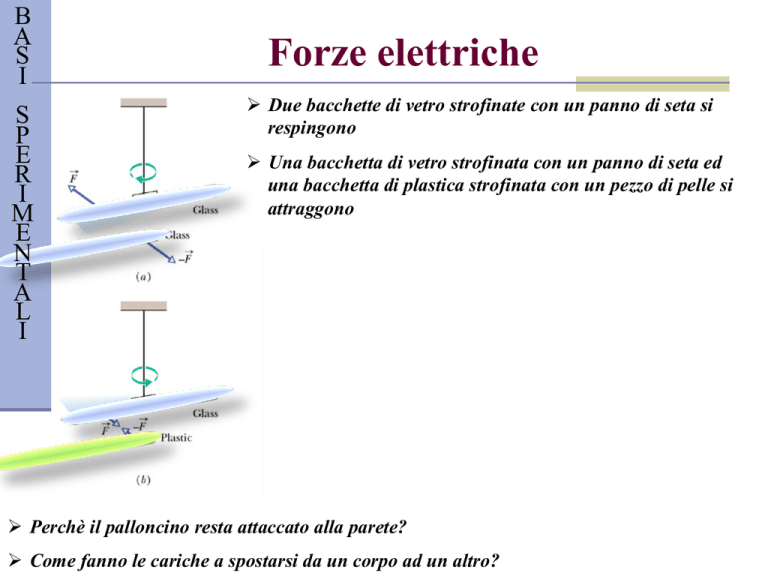
Forze elettriche
Ø Due bacchette di vetro strofinate con un panno di seta si
respingono
Ø Una bacchetta di vetro strofinata con un panno di seta ed
una bacchetta di plastica strofinata con un pezzo di pelle si
attraggono
https://phet.colorado.edu/it/simulations/category/physics/electricity-magnets-and-circuits
Ø Perchè il palloncino resta attaccato alla parete?
Ø Come fanno le cariche a spostarsi da un corpo ad un altro?
+ + + + + + + + +
- - - - - - - - - - -- - - - - - - - + + + + + + + + +
+ + + + + + + + +
- - - - - - - - -
+ + + + + + + + +
- - - - - - - - -
I
N
T
E
R
P
R
E
T
A
T
I
V
O
Ionizzazione
- - - - - - - - -
M
O
D
E
L
L
O
+ + + + + + + + +
+ + + + + + +
- - - - - - -
+ + + + + + +
- - - - - - -
+ + + + + + +
- - - - - - -
+ + + + + + +
- - - - - - -
I
N
T
E
R
P
R
E
T
A
T
I
V
O
Polarizzazione
- - - - - - -
M
O
D
E
L
L
O
+ + + + + + +
M
O
D
E
L
L
O
I
N
T
E
R
P
R
E
T
A
T
I
V
O
Conduttori e isolanti
n Isolanti = corpi in cui le cariche elettriche non possono
muoversi liberamente, ma sono vincolate dal legame
chimico a restare legate all’atomo/molecola di appartenenza
n Esempi di isolanti sono il vetro, la plastica, la gomma, etc.
n Conduttori = corpi in cui sono presenti cariche che possono
muoversi liberamente nel materiale
n
n
Nei metalli le cariche libere sono gli elettroni di conduzione
Nelle soluzioni elettrolitiche le cariche libere sono gli ioni
positivi e negativi
n La Terra può essere immaginata
come un enorme conduttore
n
Se un corpo carico è collegato a
terra mediante un conduttore, le
cariche in eccesso tendono a
neutralizzarsi ed il corpo si scarica
++
I
N
T
E
R
P
R
E
T
A
T
I
V
O
MISURA DELLA
CARICA
Misure sistematiche
occorre trovare il modo di quantificare e misurare
la CARICA e la FORZA:
- depositare cariche uguali dello stesso segno
- depositare cariche uguali di segno opposto
- depositare multipli noti di carica
GENERARE UNA CARICA PER INDUZIONE
INDURRE DUE
CARICHE UGUALI
DI SEGNO OPPOSTO
GENERARE DUE CARICHE
UGUALI DELLO STESSO SEGNO
0
+
M
O
D
E
L
L
O
-
M
O
D
E
L
L
O
I
N
T
E
R
P
R
E
T
A
T
I
V
O
la bilancia di torsione
III Newton
+Q
-F
r
-q
F
libera
Μtor ∝ Δθ
Mtor = MCoul
MCoul = Fbraccio
ferma
!
!
q1q 2 ⎛ r ⎞
F=k 2 ⎜ ⎟
r ⎝r⎠
misure imprecise (qualche %)
corpi non puntiformi (rispetto alla distanza)
difficile stabilire il valore della potenza di r
difficile valutare l’esatta direzione della forza
qQ
|F|= k 2
r
M
O
D
E
L
L n L’unità di misura della carica elettrica nel SI è il Coulomb (C)
O
n Nel SI la carica elettrica è in realtà una grandezza derivata
I
N
n Per ragioni pratiche (QUALI?) si preferisce definire come
T
grandezza fondamentale l’intensità di corrente I, misurata in
E
R
Ampere (A)
P
R
n L’equazione dimensionale della carica è [Q]=[IT]
E
T
n Nelle unità di misura del SI [C]=[As]
A
T n La costante sperimentale k nella legge di Coulomb ha lo stesso
I
significato di G nella legge gravitazionale e vale 9×109 Nm2/C2
V
O
n Per semplificare molte formule è conveniente esprimere la
Unità di misura
costante k come k=1/4πε0 dove ε0=8,85×10-12 C2/(Nm2)
n La legge di Coulomb risulta così espressa nella forma:
!
F=
!
1 q1q2 ⎛ r ⎞
⎟
2 ⎜
4 πε0 r ⎝ r ⎠
C
O
N
S
E
G
U
E
N
Z
E
Electro vs Graviton
!
!
m1m 2 ⎛ r ⎞
Fgr = −G
⎜ ⎟
2
r
⎝r⎠
G = 6,67 ×10 −11 Nm 2 kg −2
[
!
!
q1q 2 ⎛ r ⎞
Fel = k 2 ⎜ ⎟
r ⎝r⎠
k = 8,98 ×10 9 Nm 2C−2
[
Può generare e
controllare elettricità
]
]
qe = qp ∼10-19 C
∼10 m42
Fel
m 10
≈∼104×
Fgr m ∼ m ∼ 10 kg
-10
-14
Centrale
Proporzionale a r-2
Sia attrattiva sia repulsiva
Esercitata solo tra i corpi carichi
Può controllare la
gravità con la mente
Centrale
Proporzionale a r-2
me∼ 10-30 kg
Solo attrattiva
Esercitata tra tutti i corpi pesanti
p
n
-27
C
O
N
S
E
G
U
E
N
Z
E
Cosa tiene insieme la materia?
Sia Fgr che Fel consentono un modello orbitale per l’atomo, ma
Fel è decisamente dominante. Fel tiene anche insieme le molecole.
La carica elettrica si conserva sempre, per esempio nelle reazioni
chimiche o nucleari. Cosa succederebbe se così non fosse?
La Fel tra i protoni nel nucleo è repulsiva, non bilanciata dalla
Fgr tra essi. Cosa tiene unito il nucleo dell’atomo?
mT ∼ 6×1024 kg
Fe = Fg se
qT =qL≈1013 C
La Fgr determina le orbite dei
corpi celesti.
Cosa succederebbe se
corrispondente a soli macroscopicamente i corpi
1032 atomi ionizzati, celesti non fossero e non si
un atomo ogni 1018 mantenessero elettricamente
3
circa
un
m
NEUTRI?
-2
mL ∼ 10 mT
(esercizio 25.31)
C
O
N
S
E
G
U
E
N
Z
E
Valori tipici di cariche elettrostatiche
E
S
E
M
P
I
N
U
M
E
R
I
C
I
Sovrapposizione degli effetti
!
1 q q1 !
1 q q2 !
1 q qN !
F=
u r1 +
u r 2 + ... +
u rN
2
2
2
4πε 0 r1
4πε 0 r2
4πε 0 rN
q1
!
F=
+
q2
F2
F3
+
q
=
+
q
q3
+
F4
F1
q4
qi !
u ri
∑
2
4π ε 0 i ri
q
F
F = F1 + F 2 + F 3 + F 4
…ma le singole cariche
sono di dimensioni
‘atomiche’ e sono spesso
distribuite su scale
macroscopiche. In questi
casi la sommatoria viene
sostituita da un integrale
E
S
E
M
P
I
N
U
M
E
R
I
C
I
ESERCIZI
25.8 – Si trovino le componenti orizzontale e verticale ella forza elettrica risultante
agente sulla carica in basso a sinistra del quadrato in figura. Si assuma q = 1,13 uC
e a = 15,2 cm. Le cariche siano ferme.
y
(+q)
1
F
( −2 q )
F2
(−q )
F2
F3
1 2q 2
=−
= −2 f
2
4πε 0 a
1 4q 2
=
=4f
2
4πε 0 a
1 q2
=
= f = 0, 036N
2
4πε 0 a
F1x(+q) = 0 F1
x
F3
F1y(+q) = −2 f
F2( x−2 q ) = 4 f
F2( y−2 q ) = 0
F
α
f
2
Fx = 0,169N
F3x( − q ) =
f
2
Fy = −0, 046N
F3y( − q ) =
F = Fx2 + Fy2 = 0,176N
tan α =
Fy
= −0, 275
Fx
α = −15, 4°
E
S
E
M
P
I
ESERCIZI
25.4 - .
N
U
M
E
R
I
C
I
T+F+P =0
x : T sin θ = F
y : T cosθ = mg
x
F
1
q2
tan θ =
=
=
2L mg 4πε 0 mgx 2
⎛ L q ⎞
x =⎜
⎟
⎝ 2πε 0 mg ⎠
2
T
1
3
F
P
1
2
⎛
mgx ⎞
−8
q = ⎜ 4πε 0
⎟ = 2,15.10 C
2L ⎠
⎝
3
I
N
T
E
R
A
Z
I
O
N
E
Trill your mind
Gli esperimenti di strofinio con le bacchette di plastica e di vetro
e con i panni di seta e di pelle potrebbero essere anche spiegati
pensando alla presenza di 4 diversi tipi di cariche invece che 2?
Perché strofinando con le dita una moneta questa non sembra
caricarsi?
La forza elettrica che una carica esercita su una carica vicina,
cambia se vengono avvicinate altre cariche?
Perché nei conduttori le cariche libere non attraversano la
superfice ed escono?
Come si può verificare se una bacchetta isolata da terra sia
carica o meno, e stabilire il segno della carica?
I
N
T
E
R
A
Z
I
O
N
E
Linee di forza
Lines of Force for Two Point Charges
charge q 1
- 1.
charge q 2
1.
1.5
1.0
0.5
0.0
q2
q1
- 0.5
- 1.0
- 1.5
-2
-1
0
1
2
http://demonstrations.wolfram.com/LinesOfForceForTwoPointCharges/
I
N
T
E
R
A
Z
I
O
N
E
Van der Graaf
http://demonstrations.wolfram.com/VanDeGraaffGenerator/
http://demonstrations.wolfram.com/WimshurstMachine/
E
S
E
M
P
I
N
U
M
E
R
I
C
I
Distribuzioni continue
Il numero di cariche solitamente coinvolte nei fenomeni
elettromagnetici è così alto che ha senso considerare campi
generati da distribuzioni continue
q0
r-r’
dq
r
O
r’
La forza infinitesima dF su q0 dovuta
all’elemento infinitesimo di carica dq vale
dF(r) = q0 dq
r − r'
4πε 0 r − r'
3
ma se la carica elettrica minima è quella elementare,
come può esistere la carica infinitesima dq?
E
S
E
M
P
I
N
U
M
E
R
I
C
I
Densità Lineare di carica
Carica totale sul filo
linea l
Carica Q
Q=
∫
l
λ dl
Densità lineare di carica
dq
λ=
dl
dq
dl
F(r) = q0 ∫ λ (r' )dl '
l
r − r'
4πε 0 r − r'
3
E
S
E
M
P
I
Densità Superficiale di carica
Carica totale sulla superficie
Superficie S
N
U
M
E
R
I
C
I
Carica Q
Q=
∫
S
σ dS
Densità superficiale di carica
dq
σ=
dS
F(r) = q0 ∫ σ (r' )dS '
S
dS
dq
r − r'
4πε 0 r − r'
3
E
S
E
M
P
I Determinare la forza su una carica puntiforme Q1=50µC posta in P,
N a 5 m sull’asse z, dovuta ad un disco uniformemente carico, con
U carica Q=500 π µC e raggio 5 m
M
Calcoliamo la densità superficiale di carica
!
E
R
dF
Q
2
I
ρ
=
=
20
µ
C
/
m
s
2
C
πR
I
Esercizio
d
Scegliamo l’elemento infinitesimo di superficie
più comodo per i calcoli (in base alla simmetria
del problema) : dS = r dr dφ
P
rp
z
r
dφ
φ
dQ = ρ s r dr dφ
Calcoliamo la distanza rP da un elemento di
carica in coordinate ‘comode’, per esempio
cilindriche (r, φ, z) PERCHE’?
!
!
r p = P − (r 0 0) = (− r 0 d )
!
rp = r 2 + d 2
E
S
E
M
P
I
N
U
M
E
R
I
C
I
Esercizio
!
! Q ρ ds rp
dF = 1
3
!
4πε 0 rp
Il contributo infinitesimo alla forza risultante
dovuto all’elemento di superficie carico dq è
!
dF
La sovrapposizione (integrale di superficie) degli effetti di tutti
gli elementi restituisce la forza cercata:
d
rp
dφ
Ma solo la
!
componente
assiale (lungo F =
z) contribuisce
all’integrale, la
somma di tutte
2π
le componenti
=
radiali è nulla
0
(PERCHE’?)
dQ = ρ s r dr dφ
2π R
∫∫
0
R
∫∫
0
0
!
Q1ρ s r drdφ ( rp ⋅ u z ) !
uz
2
2
4πε 0 (r + d )
rp
!
r
⋅
u
( p z)
rp
Q1ρ s r drdφ rp
2
rp
4πε 0 rp
= cosθ = d / rp = d / (r 2 + d 2 )
1
2
E
S
E
M
P
I
N
U
M
E
R
I
C
I
Esercizio
R
! Q ρ d 2π
!
r dr
1 s
dφ ∫ 2
u
Risolviamo l’integrale: F =
∫
2 3/2 z
4πε 0 0
0 (r + d )
!
dF
d
rp
R
⎤
!
Q1ρ s ⎡
d
=
dφ u z
⎢− 2
⎥
∫
4πε 0 0 ⎣
r + d 2 ⎦0
!
Q1ρ s ⎛
1
1⎞!
=
d ⎜−
+ ⎟ u z = 16, 5N u z
2ε 0 ⎝
R2 + d 2 d ⎠
2π
dφ
dQ = ρ s r dr dφ
E
S
E
M
P
I
N
U
M
E
R
I
C
I
Densità di carica in un volume
Volume V
Ca rica Q
Carica totale distribuita nel volume V
con densità uniforme
Q=
∫
V
ρ dV
dq
ρ=
dV
dV
F(r) = q0 ∫ ρ (r' )dV '
V
dq
dq = ρ(r’) dV’
r − r'
4πε 0 r − r'
Integrale di difficoltà enorme!
3
M
O
D
E
L
L
O
I
N
T
E
R
P
R
E
T
A
T
I
V
O
Coulomb > campo elettrico
+q +q
+Q
p
qQ
Fp= k 2 ur
r
Fp = k Q u
r
q
r2
qQ
Fp= k 2 ur
r
Fp = k Q u
r
q
r2
§ F è misurabile solo in presenza di entrambe le cariche Q e q
§ Se cambia una delle due cariche cambia anche la forza
ur
Q
Ep= F = k 2 ur [N/C]
q
r
Per convenzione ha il verso della forza
che agirebbe su di una carica positiva
§ E è misurabile anche solo in presenza della carica Q
§ NON dipende dal valore della carica posta nel punto p
§ E’ una proprietà dello spazio ( r ) determinata dalla
distribuzione di TUTTE le cariche (Q) tranne quella in p
M
O
D
E
L
L
O
I
N
T
E
R
P
R
E
T
A
T
I
V
O
Campi scalari e vettoriali
M
O
D
E
L
L
O
I
N
T
E
R
P
R
E
T
A
T
I
V
O
Misura del campo elettrico
Il campo si misura a partire dalla misura della forza.
La misura della forza dipende però anche dalla carica che c’è in P.
Occorre fare in modo che il valore della carica in P NON abbia
influenza sulla misura.
!
!
F
E p = lim
q →0 q
Ma quanto piccola può essere una carica perché la
misura sia attendibile, cioè aderente alla definizione?
B
A
S
I
S
P
E
R
I
M
E
N
T
A
L
I
Millikan
!
E
!
!
FC = −qE
!
!
FR = −6πrηv
!
!
P = mg
mg
FR = P ⇒ vl =
6πrη
dalla misura di vl si ricava r
e = 1.60217657 x 10-19 C
6π rη ( vl − v )
P − qE
= q = ne
qE + FR = P ⇒ v =
E
6π rη
la carica “di prova” non può essere < e, ma in genere e è
qE
vl − v =
sufficientemente piccola da essere considerata (quasi) nulla
6π rη
B
A
S
I
S
P
E
R
I
M
E
N
T
A
L
I
Rappresentazione del campo elettrico
https://phet.colorado.edu/en/simulation/charges-and-fields
+3
-1
§ In ciascun punto sono tangenti al vettore campo elettrico
§ Sono uscenti dalle cariche positive ed entranti in quelle negative
§ La loro densità è proporzionale all’intensità del campo
§ Non indicano la traiettoria seguita dalle cariche
E
S
E
M
P
I
Un caso speciale : dipolo elettrico
N
U
M
E
R
I
C
I
E y = E+ y + E− y
12
dove r± = !" x 2 + (y a)2 #$
ya
sin θ ± =
r±
cosθ ± =
r2
x
r±
s
E
S
E
M
P
I
campo vicino alle cariche
N
U
M
E
R
I
C
I
q "$ y − a
y + a %'
Ey =
−
32
32'
3$
4πε 0 r # (1+ s− )
1+
s
( +) &
%
qy "$
1
1
'
=
−
32
32'
3$
4πε 0 r # (1+ s− )
(1+ s+ ) &
%
qa "$
1
1
'
−
+
32
32'
3$
4πε 0 r # (1+ s− )
(1+ s+ ) &
!
E = E x î + E y ĵ
poiché q e a compaiono indipendentemente
in termini additivi e non solo a prodotto, da
queste misure si può ricavare sia il valore
della carica q che della distanza a
⎛
⎞
qx ⎜ 1
1 ⎟
Ex =
−
4πε 0 r 3 ⎜⎜ 1+ s 23 1+ s 23 ⎟⎟
( +) ⎠
⎝(
−)
E
S
E
M
P
I
N
U
M
E
R
I
C
I
campo lontano dalle cariche
r >> a ⇒ s → s0 = 0
Serie di Taylor
f (s ≈ s0 ) = f (s0 ) + f '(s0 )(s − s0 ) +
1
f ''(s0 )(s − s0 )2 +
2
in coordinate sferiche
x = rsinθ; y = rcosθ
(problema 26.2)
N
U
M
E
R
I
C
I
Dipolo elettrico
x
momento
di dipolo
z
y
+q asse di simmetria
per rotazione
-q
piano di simmetria
con inversione di carica
E
S
E
M
P
I
Da lontano le
cariche NON sono
distinguibili
separatamente.
La misura del
campo consente di
ricavare
SOLAMENTE il
MOMENTO DI
DIPOLO (e non il
valore di q e a)
che diventa
l’unica grandezza
fisica rilevante.
A
P
P
L
I
C
A
Z
I
O
N
I
Approssimazione di monopolo
Qualsiasi distribuzione di carica
elettrica complessivamente NON
nulla, per distanze sufficientemente
grandi, si comporta come una carica
singola puntiforme di valore pari alla
carica netta della distribuzione
Misurando la distribuzione del campo elettrico lontano dalla
sorgente, se troviamo una distribuzione a simmetria sferica
con linee APERTE, siamo in grado solamente di stimare la
carica NETTA della distribuzione, non il valore e la
disposizione delle cariche.
A
P
P
L
I
C
A
Z
I
O
N
I
Approssimazione di dipolo
Qualsiasi distribuzione di carica
elettrica complessivamente nulla, con
simmetria assiale, per distanze
sufficientemente grandi, di comporta
come un singolo dipolo elettrico e può
essere completamente caratterizzata solo
in termini del suo momento di dipolo
Misurando la distribuzione del campo elettrico lontano dalla
sorgente, se troviamo una distribuzione a simmetria cilindrica
con linee CHIUSE, siamo in grado solamente di stimare il
MOMENTO di DIPOLO della distribuzione, non il valore
delle cariche e la loro disposizione.
poiché tutti gli atomi e le molecole non ionizzati sono neutri, la loro interazione è in genere di
tipo dipolo-dipolo, e anche in presenza di una campo esterno, è il mom di dipolo che conta
A
P
P Campo
L
I
C
A
Z
I
O
N
I
elettrico sull’asse di un disco carico
Avevamo ottenuto:
! Q1 ρ s
F=
2ε 0
Per cui:
!
ρs
E=
2ε 0
⎛
d⎜−
⎜
⎝
⎛
d⎜−
⎜
⎝
Casi Limite
1
R2 + d 2
1
1 ⎞⎟ !
+ uz
d ⎟⎠
1 ⎞⎟ !
+ uz
d ⎟⎠
R2 + d 2
!
ρs !
Quando d = 0
E=
uz
2ε 0
al centro del disco
A
P
P Campo elettrico sull’asse di un disco carico
L
I
Casi Limite
C Quando d >> R
A
⎛
⎞
lontano lungo l’asse
Z
⎜
⎟
I
⎞!
! ρs ⎛
!
ρs ⎜
1
⎟
d
O
⎜
⎟
−
+ 1⎟u z
E=
−
+1 u z ≈
2
⎜
2ε 0
⎟
N
2
2
R
2ε 0 ⎜⎝
R
+
d
⎜
⎟⎟
⎠
1
+
I
⎜
2
⎝
R2
ρ s 2d 2
=
2ε 0
R2
1+ 2
2d
ρs
≈
2ε 0
2d
⎠
R2
Q
2
2 R2
Q
2d = πR
=
2ε 0 2d 2
1
4πε 0 d 2
dal punto P il disco viene visto come una carica puntiforme
e il campo deve rispecchiare questa condizione
A
P
P Campo elettrico sull’asse di un disco carico
L
I
C Quando R >> d
A
Z
I
⎛
⎞!
!
ρs !
ρ
d
s ⎜
⎟
O
u z Piano infinito
E=
−
+1 u z ≈
N
⎟
2ε 0 ⎜⎝
2ε 0
R2 + d 2
I
⎠
dal punto P il disco viene visto come un piano infinito
e il campo deve rispecchiare questa condizione
A
P
P
L
I
C
A
Z
I
O
N
I
Come calcolare il campo in altri casi?
computer
distribuzioni
simmetriche
A
P
P
L
I
C
A
Z
I
O
N
I
Campo elettrico lungo l’asse di un filo
dal punto P il filo viene visto come una carica puntiforme
e il campo deve rispecchiare questa condizione
(esercizio 26.18)
E
S
E
M
P
I
N
U
M
E
R
I
C
I
e fuori dall’asse…?
"
dL r
1
1
λq $
Fq = kqλ 2 =
4πε 0 $ x 2 + y 2
r
barra
#
∫
^
lungo l'asse(x1 = −x2 ) :
- per y >> L;sin θ x ≈ L y
!
kqQ
Fq ≈ − 2 ŷ
y
!
q
EQ ≈ −k 2 ŷ
y
% "
x
' x̂ − $
' $ y x 2 + y2
− x1 &
#
x2
%
' ŷ
'
− x1 &
x2
La barretta è vista come un punto
dx=dL
x
- per y << L
!
2kqQ
Fq ≈ −
ŷ
y
!
2Q
λ
EQ = k
ŷ =
r̂
yL
2πε 0 r
La barretta è vista come un filo
θx
dL = dx
r 2 = x 2 + y2
r rx − ry xx̂ − yŷ x
y
r̂ = =
=
= x̂ − ŷ
r
r
r
r
r
-q
y
r
E
S
E
M
P
I
soluzione dell’integrale
∫
N
U
M
E
R
I
C
I
dx
r2
⎛x y ⎞
⎜ x̂− ŷ ⎟ =
⎝r r ⎠
x2
∫ x1
barra
xdx
( x +y )
2
2
x̂
32
x2
− ∫ x1
ydx
2 32
( x +y )
2
ŷ
x
= tan θ x
y
2 xdx
y2
2
1° : z = ( x y) ; dz =
x
2 1/2
( x +y )
2
2
2° : z = y tan θ x ; dz = y sec θ x dθ x
= sin θ x
dx=dL
x
x2
∫ x1
xdx
( x +y )
2
x2
∫ x1
2
ydx
( x +y )
2
2
x̂ =
32
x2
∫ x1
1
ŷ = 2
32
y
dz
(
2
)
2 y z +1
x2
∫ x1
θx
x̂
32
sec 2 θ x dθ x
(tan θ +1)
2
x
32
y
dL = dx
r 2 = x 2 + y2
r rx − ry xx̂ − yŷ x
y
r̂ = =
=
= x̂ − ŷ
r
r
r
r
r
-q
ŷ
r
S
U
M
M
A
R
Y
KEEP in MIND (40%)
ü La legge di Coulomb è un fatto della natura, non una deduzione
ü F = kqQ/r2 vale solo tra cariche puntiformi
ü Il principio di sovrapposizione vale per tutte le grandezze
vettoriali e si utilizza in tutti i casi in cui sono presenti più di
due cariche o quando le cariche non sono puntiformi
ü Il principio di conservazione della carica elettrica si fonda sia
su osservazioni dirette sia su deduzioni logiche. Tutti i fenomeni
elettrostatici possono essere spiegati considerando che la carica
elettrica non si genera né si distrugge, ma si trasferisce da un
corpo ad un altro e che i corpi, per le loro proprietà elettriche,
si dividono in isolanti e conduttori (ohmici, super- e semiconduttori)
ü Le cariche elettriche restano ferme solo se sono fissate,
altrimenti non esistono punti di equilibrio stabile in sistemi
elettrostatici
S
U
M
M
A
R
Y
KEEP in MIND (40%)
ü La carica elettrica è quantizzata
ü Il momento di dipolo elettrico è la grandezza fondamentale per
la gran parte delle interazioni chimiche e delle interazioni della
materia con la radiazione
ü Il campo elettrico è un concetto astratto (per ora) utile ad
illustrare l’interazione tra cariche elettriche
ü Una carica elettrica genera sempre un campo elettrico nello
spazio circostante; una carica elettrica puntiforme q che si trova
in presenza di un campo elettrico E sente sempre una forza qE
ü Se le cariche sono distribuite, si applica il principio di
sovrapposizione considerando la carica dq contenuta in un
elemento geometrico dl, dS o dV con densità λ, σ o ρ
S
U
M
M
A
R
Y
KEEP in MIND (+40%)
ü Funzionamento della bilancia di torsione
ü Analisi dell’esperimento di Millikan
ü Campo elettrico di un filo lungo l’asse
ü Campo elettrico di un disco lungo l’asse
ü Campo elettrico di un piano infinito
ü Campo elettrico di una sfera
ü Campo elettrico di un dipolo
H
O
M
E
W
O
R
K
Home Sweet Home
Il castello errante di Howl, Y. Miazaki ©
•
•
Studiare i capitoli 25 e 26
Rispondere ai quesiti a risposta
multipla dei due capitoli
• Fare gli esercizi 25 (2, 8, 11, 16,
24) e 26 (4, 8, 13, 26, 30)
• Leggere i capitoli 27 e 28
• Costruite il vostro elettroscopio
e misurate quanta carica viene
prodotta per ionizzazione:
documentate quantitativamente
l’esperimento (mov, ppt, doc)
Consegna : 17 Marzo












