Esercitazioni 14/10/2016

Esercitazioni 14/10/2016
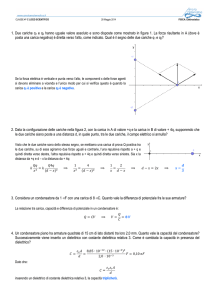
Esercizio 1
In un condensatore piano (Σ, h) viene inserita parallelamente alle armature una lastra conduttrice a facce piane e parallele, ciascuna di area Σ, e spessa x. Calcolare
di quanto varia la capacità del condensatore e quanto lavoro viene speso per inserire
la lastra, nelle due ipotesi che l'inserimento avvenga mantenendo costante la carica
sulle armature o costante la ddp tra le medesime.
h
x
Soluzione 1
Il sistema si può considerare come come due condensatori in serie, quindi la capacità
è
1
1
1
x1
x2
h−x
=
+
=
+
=
C
C1 C2
o Σ 0 Σ
0 Σ
ovvero C = 0 Σ/(h − x), mentre la capacità iniziale era C0 = 0 Σ/h.
LA PARTE CHE SEGUE NON FA PARTE DEL PROGRAMMA
Se la carica q0 è mantenuta costante, rimane costante anche il campo elettrico,
ma cambiano il potenziale e l'energia elettrostatica. Infatti
∆V =
e
q0
σ
h−x
= (h − x) = ∆V0
C
0
h
1
1 0 Σ
(h − x)2
1
W = C∆V 2 =
∆V02
= 0 ΣE02 (h − x)
2
2h−x
h2
2
1
Notiamo che si è persa una ddp di E0 x dovuta alla lastra. Il lavoro fatto dal campo
sarà opposto a quello esterno, quindi
1
L = −∆W = 0 ΣE02 x
2
Nel caso invece di ddp costante, il sistema non sarà isolato perché servirùn lavoro
dall'esterno che mi faccia passare delle cariche tra le armature per mantenere la ddp
costante. Abbiamo ∆V0 = E0 h = E(h − x), dalla quale
E = E0
h
,
h−x
q = q0
h
h−x
L'energia elettrostatica è
1
1
W = C∆V02 = 0 Σ(h − x)E 2
2
2
Il lavoro ora sarà L = ∆W = 0 ΣhE02 x/2(h − x).
Esercizio 2
Due sfere conduttrici di raggi R1 = 6 cm e R2 = 4 cm sono poste a distanza d,
molto maggiore di entrambi i raggi, e sono collegate da un sottile lo conduttore.
Una carica q = 10−9 C viene comunicata al sistema. Determinare:
1) come questa carica si distribuisce tra le due sfere;
2) l'energia elettrostatica del sistema;
3) dimostrare che la soluzione trovata rende minima l'energia elettrostatica.
Soluzione 2
1) Le due sfere sono collegate e quindi allo stesso potenziale, quindi
V1 =
q2
q2
q1
q1
+
=
+
= V2
4π0 R1 4π0 d
4π0 R2 4π0 d
Inoltre, la carica non si disperde, quindi q = q1 + q2 . Risolvendo il sistema troviamo
(
q2 =
q1 =
(d−R1 )R2
(d−R2 )R1 +(d−R1 )R2 q = 0.4
q − 0.4q = 0.6 · 10−9 C
· 10−9 C
2) W = q1 V1 /2 + q2 V2 /2, ovvero
W =
q12
q22
q1 q2
+
+
= 4.5 · 10−8 J
8π0 R1 8π0 R2 4π0 d
2
dove è stato trascurato l'ultimo termine dato che d R1 , R2 .
3) Riscriviamo l'energia elettrostatica in funzione di una sola delle due cariche
1
q1
q − q1
1
q1
q − q1
W = q1
+
+ (q − q1 )
+
2
4π0 R1
4π0 d
2
4π0 R2 4π0 d
Derivando rispetto a q1 e ponendo uguale a zero otteniamo
q1
che dà
q1 = q
1
1
2
+
−
R1 R2 d
1
2
=q
−
R2 d
(d − R2 )R1
= 0.6 · 10−9 C
d(R1 + R2 ) − 2R1 R2
uguale al valore trovato prima.
Esercizio 3
Tra le armature di un condensatore piano (Σ, h) e parallelamente ad esse viene introdotta una lastra di materiale dielettrico (Σ, y ) con costante dielettrica r . Calcolare
il rapporto tra le capacità del condensatore dopo e prima dell'inserzione.
y1
σ0
y y2
−σP σP
−σ0
Soluzione 3
La capacità iniziale è C0 = 0 Σ/h. Dopo sono in serie, quindi
1
y1
y2
y
1
=
+
+
=
[y + r (h − y)]
C
0 Σ 0 Σ 0 r Σ
0 r Σ
dove y1 + y2 = h − y . Il rapporto tra le due capacità è quindi
C
r h
=
C0
y + r (h − y)
3
Esercizio 4
Una sfera conduttrice di raggio R0 = 1 cm è circondata da un involucro sferico di
raggio interno R0 e raggio esterno R = 5 cm, con costante dielettrica r = 4. Sulla
sfera si trova una carica libera q = 10−8 C . Calcolare:
1) la densità delle cariche di polarizzazione;
2) l'energia elettrostatica del sistema.
Soluzione 4
1) Per il teorema di Gauss per il vettore induzione elettrica D, Φ(D) = 4πr2 D = q ,
quindi
q
n̂
4πr2
per r ≥ R0 . Il vettore polarizzazione è P = (r − 1)/r D. La densità di cariche di
polarizzazione superciali sarà, per r = R0 ,
D=
σP (R0 ) = P(R0 ) · n̂ = −
r − 1 q
= −5.97 · 10−6 C/m2
r 4πR02
mentre per r = R,
σP (R) = P(R) · n̂ =
r − 1 q
= 0.24 · 10−6 C/m2
r 4πR2
Le cariche di polarizzazione qP (R0 ) = 4πR02 σP (R0 ) e qP (R) = 4πR2 σP (R) sono
uguali dato che il dielettrico è omogeneo. Per lo stesso motivo la densità di carica
volumica è zero.
2) L'energia elettrostatica è data da
1
W =
2
Z
V (R)
V (R0 )
D2
1
dV +
0 r
2
Z
V (∞)
V (R)
D2
q2
dV =
[R+(r −1)R0 ] = 1.8·10−5 J
0
8π0 r RR0
dove dV = 4πr2 dr.
Esercizio 5
Un condensatore sferico (R1 = 5 cm, R2 = 10 cm) ha l'intercapedine riempita da un
dielettrico non omogeneo la cui costante dielettrica relativa varia secondo la legge
r (r) = a/r con a = 0.2 m. Sulla sfera interna c'è la carica q = 10−9 C , l'armatura
esterna è a potenziale zero. Calcolare:
1) il potenziale ad una distanza R dal centro;
2) determinare la densità delle cariche di polarizzazione.
4
Soluzione 5
1) Il vettore induzione elettrica è dal teorema di Gauss è D, Φ(D) = 4πr2 D = q ,
quindi
D=
q
n̂
4πr2
e conseguentemente il campo elettrico
E=
q
D
=
n̂
0 r
4π0 ar
Sappiamo che V (R2 ) = 0, quindi
Z
R2
V (R) − V (R2 ) =
E · dr =
R
q
R2
ln
4π0 a
R
2) Il vettore polarizzazione è
P=
r − 1
q a−r
D=
n̂
r
4πa r2
e quindi le σP sono, sulle due facce del dielettrico,
σP (R1 ) = P(R1 ) · n̂ = −
e
σP (R2 ) = P(R2 ) · n̂ =
q a − R1
= −2.39 · 10−8 C/m2
4πa R12
q a − R2
= 0.40 · 10−8 C/m2
4πa R22
Il dielettrico non è omogeneo e quindi le cariche superciali qP non saranno uguali
e pari a qP (R1 ) = −0.75 · 10−9 C/m2 e qP (R2 ) = 0.50 · 10−9 C/m2 . La densità
volumica di cariche nel dielettrico sarà diversa da zero dato che non è omogeneo,
ρP = −∇ · P. P dipende solo da r, e quindi in coordinate sferiche ci interessa solo
la componente radiale del gradiente.
q
a−r
q 1
ρP = −
∇r
=
2
4πa
r
4πa r2
quindi le cariche di volume sono
Z
qvol =
ρP dV =
q
(R2 − R1 ) = 0.25 · 10−9 C
a
Notare che qvol + qP (R1 ) + qP (R2 ) = 0, infatti il dielettrico è scarico e le cariche
sono solo ridistribuite al suo interno e sulla sua supercie.
5