1) Una particella si trova in x = +5 m
nell’istante t = 0 s, in x = -7 m
nell’istante t = 6 s, e in x = +2 m
nell’istante t = 10 s. Si trovi la
velocità
media
della
particella
durante gli intervalli (a)t = 0 s, t =
6 s; (b) t = 6 s, t = 10 s; (c) t = 0
s, t = 10 s
2) Due treni partono da una stazione A ad
intervallo di tempo 10 min.Il primo raggiunge la
stazione B dopo un tempo 2.5 h, viaggiando con
velocità costante 100 km/h. Quale deve essere la
velocità del II treno affinché raggiunga B nel
medesimo istante del primo treno.
R 30 m/s
7) Un’ audace donna acrobata seduta
sul
ramo
di
un
albero,
vuole
lasciarsi cadere verticalmente sulla
groppa di un cavallo che passa al
galoppo sotto l’albero. La velocità
del cavallo è 10 m/s, e la distanza
dal ramo alla sella è 3 m. (a) a
quale distanza, in direzione orizzontale, deve trovarsi la sella dal
ramo, nell’istante in cui la donna
inizia a muoversi? (b) Per quanto
tempo essa rimane in aria?
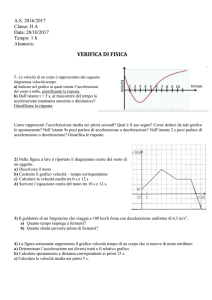
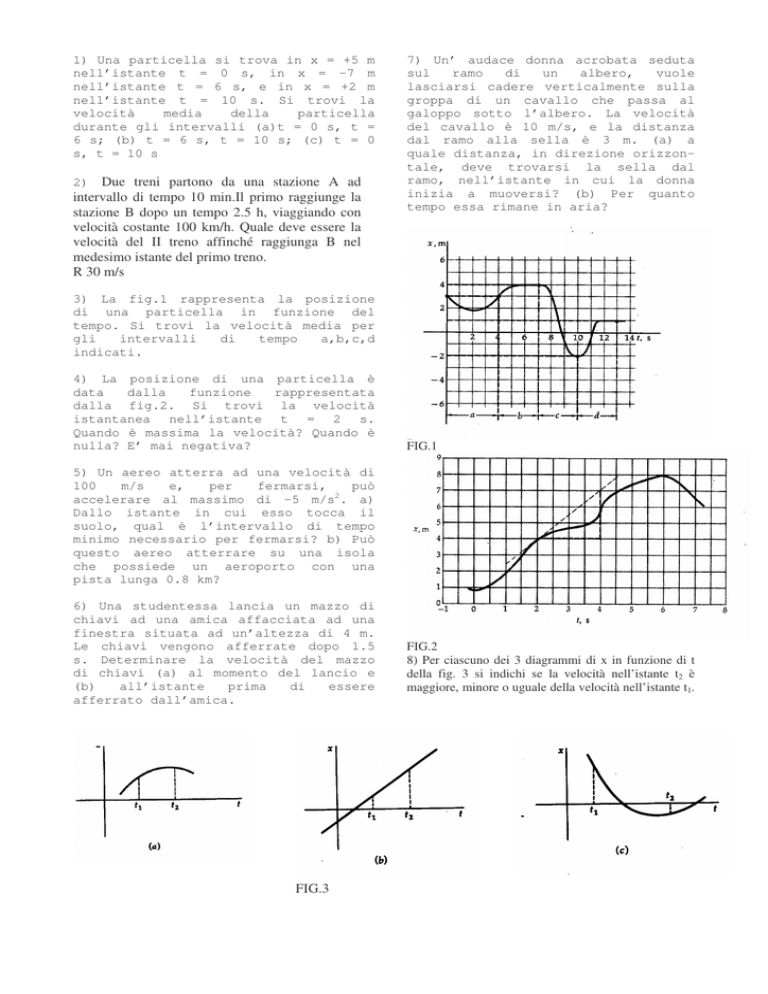
3) La fig.1 rappresenta la posizione
di una particella in funzione del
tempo. Si trovi la velocità media per
gli
intervalli
di
tempo
a,b,c,d
indicati.
4) La posizione di una particella è
data
dalla
funzione
rappresentata
dalla fig.2. Si trovi la velocità
istantanea nell’istante t = 2 s.
Quando è massima la velocità? Quando è
nulla? E’ mai negativa?
FIG.1
5) Un aereo atterra ad una velocità di
100
m/s
e,
per
fermarsi,
può
accelerare al massimo di –5 m/s2. a)
Dallo istante in cui esso tocca il
suolo, qual è l’intervallo di tempo
minimo necessario per fermarsi? b) Può
questo aereo atterrare su una isola
che possiede un aeroporto con una
pista lunga 0.8 km?
6) Una studentessa lancia un mazzo di
chiavi ad una amica affacciata ad una
finestra situata ad un’altezza di 4 m.
Le chiavi vengono afferrate dopo 1.5
s. Determinare la velocità del mazzo
di chiavi (a) al momento del lancio e
(b)
all’istante
prima
di
essere
afferrato dall’amica.
FIG.3
FIG.2
8) Per ciascuno dei 3 diagrammi di x in funzione di t
della fig. 3 si indichi se la velocità nell’istante t2 è
maggiore, minore o uguale della velocità nell’istante t1.
Cinematica: moto in una dimensione
11) Un temerario nel 1993 si è buttato dalla cascate del Niagara. L'
altezza di caduta era 48 m. Assumiamo
che la sua velocità iniziale fosse nulla e trascuriamo gli effetti della resistenza dell'
aria. a) quanto è durato il
volo di caduta? quale era la velocità finale?
R 3.1 s, 31 m/s
12) Due treni partono nello stesso istante da due stazioni A e B distanti 400 km. Il primo treno, che parte da
A verso B si muove alla velocità di 80 km/h e il secondo che parte da B verso A alla velocità di 30 m/s.
Supponendo che si muovano con velocità costante, rappresentare i due moti in un diagramma orario e
calcolare l’istante in cui si incontrano.
R = 2.13 h
13) Un elettrone, con velocità iniziale di 104 m/s attraversa una regione di 1 cm dove è accelerato
elettricamente. Ne esce con una velocità di 4 x 106 m/s. Quale è stata la sua accelerazione supponendola
costante.
R 8 x 1014 m/s2
14) Un mesone arriva con velocità di 5 x 106 m/s in una regione dove un campo elettrico produce
un'
accelerazione di 1.25 x 1014 m/s2 in direzione opposta alla velocità iniziale del mesone. Quale spazio
percorre il mesone prima di fermarsi?
R 0.1 m
15) Un pallone è lanciato verticalmente verso l'
alto dal suolo con una velocità di 29.4 m/s. Quanto tempo
impiega per raggiungere il punto più alto? Quale è la massima altezza raggiunta ? In quali istanti sarà a 39.2
m sopra il suolo? In quale istante tocca il suolo?
R 3 s; 44.1 m; 2 e 4 s; 6 s
16) Un razzo è lanciato verticalmente e sale con accelerazione verticale costante di 20 m/s2 per 1 minuto.
Dopo questo tempo esso continua a salire come un corpo libero. Calcolare la massima altezza raggiunta e il
tempo totale di lancio. R 110 km, 332 s
17) Avvistando una pattuglia della polizia stradale, frenate la vostra Porsche da 100 km/h a 80
km/h nello spazio di 88 m con accelerazione costante. a) quanto vale l'
accelerazione? b) per quanto
tempo dovete frenare?
R = 1.58 m/s2 (opposta a v) ; 3.5 s
18) Una sonda è lasciata cadere in un lago da una piattaforma posta 5 m sull'
acqua. Essa colpisce l'
acqua con
una certa velocità e raggiunge il fondo con la stessa velocità 5 s dopo che è stata lasciata. a) quanto è
profondo il lago; b) si supponga di aspirare tutta l'
acqua del lago, con quale velocità iniziale deve essere
lanciata la sonda dalla piattaforma per toccare il fondo in 5 s. (assumere g=10 m/s2 )
R a) 40 m b) 16 m/s verso l'
alto
19) Un uomo sta sul tetto di un edificio e lancia un grave verticalmente verso l'
alto con una velocità di 12
m/s; il grave tocca il suolo dopo 4 s. Calcolare: a) la massima quota raggiunta; b) l'
altezza dell'
edificio c) la
velocità finale (altezze calcolate rispetto al suolo)
R a) 39.2 m b) 32 m c) 28 m/ verso il basso
20) Un sasso è lanciato verso l'
alto e ricade nel punto di partenza dopo 10 s. Calcolare la velocità iniziale, la
velocità di arrivo e la massima quota raggiunta. (assumere g=10 m/s2 )
R a) 50 m/s b) 50 m/s verso il basso c) 125 m
21) Con quale velocità deve essere lanciata verso l'
alto un oggetto per poter salire fino a 50 m. Per quanto
tempo resterà in aria.
R 31.3 m/s , 6.4 s
Cinematica: moti piani
22) Una palla da baseball è lanciata verso un giocatore con velocità iniziale di 20 m/s e sotto un angolo di
45° con l'
orizzontale. Nell'
istante in cui la palla viene lanciata, il giocatore si trova a 50 m dal lanciatore.
Con quale velocità e in quale direzione deve correre per afferrare la palla alla stessa altezza a cui è stata
lanciata?
R 3.2 m/s verso la palla
23) Un proiettile è sparato nell'
aria dalla sommità di una rupe alta 180 m sopra la valle. La sua velocità
iniziale ha il modulo di 60 m/s e forma un angolo di 60° con l'
orizzontale. Calcolare il punto in cui il
proiettile raggiunge il suolo. (Trascurare la resistenza dell'
aria).
R 393 m
24) Un bombardiere, in picchiata ad un angolo di 60° con la verticale, lascia cadere un bomba da un'
altezza
di 700 metri. La bomba colpisce il suolo 5 s dopo il lancio. Calcolare la velocità del bombardiere e lo
spostamento orizzontale della bomba durante il volo.
R 231 m/s ; 1000 m
25) Un cannone, posto a 300 m di altezza, riesce a colpire un bersaglio di coordinate (150 m, 200 m) quando
il suo angolo di tiro è 45°. Calcolare il modulo della velocità del proiettile 1) alla bocca del cannone ; 2)
quando colpisce il bersaglio. R 29.7 m/s ; 53.3 m/s
26) Un ragazzo, in piedi a 4 m di distanza da una parete verticale, lancia una palla. La palla è lanciata a 2 m
dal suolo con velocità di 10√2 m/s e angolo di 45°. Quando la palla colpisce la parete la componente x della
velocità si inverte e la componente y resta invariata. Calcolare il punto in cui la palla colpisce il suolo.
R 18 m
27) Uno sciatore lascia la rampa di salto con una velocità di 10 m/s formante un angolo 15° con
l'
orizzontale. La discesa forma un angolo di 50° con l'
orizzontale e la resistenza dell'
aria è trascurabile.
Trovare la distanza alla quale atterra lo sciatore sulla discesa e le componenti della velocità all'
atterraggio.
R 43.2 m; 9.7 m/s e 25.6 m/s verso il basso
28) Un coniglio attraversa di corsa un parcheggio nel quale è stato tracciato un sistema di assi coordinati
(?!). Il suo percorso è tale che le componenti della sua posizione rispetto all'
origine delle coordinate sono
date, in funzione del tempo, dalle espressioni
x = -0.31t2 + 7.2 t + 28 metri
y = 0.22 t2 – 9.1t + 30 metri
a) per t = 15 s calcolate il vettore posizione del coniglio in coordinate cartesiane e polari.
Determinare la velocità del coniglio per t = 15 s in coordinate cartesiane e polari.
Determinare l'
accelerazione per t = 15 s in coordinate cartesiane e polari.
29) Una particella con velocità iniziale v0 = -2 ux+ 4 uy (m/s) subisce un'
accelerazione costante di intensità a
2
= 3 m/s , il cui vettore forma un angolo θ = 130° rispetto alla direzione positiva dell'
asse x. Quale è la
velocità della particella, espressa in coordinate cartesiane e con ampiezza e direzione, per t = 5 s?
30) Un aereo da soccorso vola a 198 km/h alla quota di 500 m verso un punto posto sulla verticale di una
persona che si dibatte in mare. Il pilota vuole sganciare il salvagente in modo che cada in acqua molto vicino
al naufrago. Sotto quale angolo visuale φ il pilota deve sganciare il salvagente? stabilire la velocità del
salvagente al momento dell'
impatto.
R 48°, vx = 55 m/s vy = 99 m/s verso il basso
31) Una nave pirata è ormeggiata a 560 m da un forte. Il cannone del forte è piazzato a livello del mare, ha
una velocità v0 di uscita di 82 m/s. A quale angolo di elevazione si deve puntare il cannone per colpire la
nave pirata? A quale distanza dal forte deve portarsi la nave pirata per essere fuori della portata di tiro del
cannone. R 27° e 63°, >686 m
Moto circolare
32) Determinare la velocità e l’accelerazione di un corpo sulla superficie terrestre al variare della latitudine
θ. (Raggio della terra 6400 km)
R 465 cos θ m/s; 0.034 cos θ m/s2
33) Il treno veloce TGV viaggia ad una velocità media di 216 km/h. Se abborda una curva a questa velocità
e la massima accelerazione tollerabile dai passeggeri è 0.05 g quale deve essere il minimo raggio
ammissibile per le curve dei binari? Se una curva ha un raggio di 1 km a quale valore deve essere ridotta la
velocità del treno per non superare l’accelerazione tollerabile?
R 7.35 km; 22 m/s
34) Un orologio (analogico) segna le 12. Calcolare le velocità angolari della lancetta dei minuti e di quella
delle ore. Determinare dopo quanto tempo le lancette saranno nuovamente sovrapposte.
R 1.7 x 10-3 e 1.5 x 10-4 rad/s; 3927 s
35) Qual è l’accelerazione centripeta dovuta alla rotazione della terra per un corpo posto all’equatore. Quale
dovrebbe essere il periodo di rotazione della terra affinché l’accelerazione centripeta abbia lo stesso valore
dell’accelerazione di gravità. (Raggio della terra 6400 km).
R 0.034 m/s2, 84 min
36) Un satellite terrestre si muove su un'
orbita circolare di 600 km sopra la superficie terrestre. Il periodo di
rivoluzione è 98 min.Calcolare l'
accelerazione di gravità dell'
orbita (accelerazione centripeta).
R 8 m/s2
37) L'
orbita della luna attorno alla terra è approssimativamente circolare con un raggio medio di 3.84 x 108
m. Il periodo di rivoluzione è 27.3 giorni. Trovare la velocità orbitale media e la sua accelerazione
centripeta. Trovare le stesse grandezze per il moto di rivoluzione della terra attorno al sole (raggio medio 1.5
x 108 km, periodo 365 g)
R 1000 m/s, 0.0026 m/s2 , 3 x 104 m/s2 , 0.0060 m/ s2
38) Due punti materiali si muovono su due circonferenze concentriche di raggio R1 = 5 m e R2 = 10 m con la
stessa velocità v = 10 m/s. Calcolare i due periodi. Se i punti sono partiti allineati all’istante t = 0 in quale
istante saranno nuovamente allineati.
39) Un punto, partendo dalla quiete, si muove lungo un cerchio di raggio 10 cm con accelerazione
tangenziale costante. Trovare detta accelerazione se la sua velocità dopo 2 rivoluzioni dall'
inizio del
movimento è 80 cm/s.Calcolare tale istante.
R 25.5 cm/s2, 3.1 s
40) Un punto materiale si muove su una circonferenza di raggio 1 m con accelerazione tangenziale costante.
Trovare detta accelerazione sapendo che il vettore accelerazione forma un angolo di 60° con la direzione
della velocità 2 s dopo l'
inizio del moto. Il corpo parte da fermo.
R 0.43 m/s2
41) Un punto materiale è in moto su una circonferenza di raggio R = 2 m con accelerazione tangenziale
costante at = 3 m/s2. All'
istante t* il modulo dell'
accelerazione (totale) è 5 m/s2, trovare in tale istante
2
l'
accelerazione centripeta e la velocità. R 4 m/s , 2.2 m/s
42) Un punto su una circonferenza di raggio 10 cm si muove con la legge oraria θ = 6t3 rad. Determinare il
modulo della velocità e dell'
accelerazione del punto nell'
istante in cui l'
accelerazione tangenziale è uguale a
quella centripeta. R 0.42 m/s, 2.4 m/s2
43) Un punto materiale si muove su una circonferenza di raggio R = 150 cm con accelerazione tangenziale
costante at = 5 m/s2 partendo dalla quiete. In quale istante t* il punto raggiunge la velocità di 5 m/s? Quanti
giri ha percorso? Quanto vale il modulo dell’accelerazione? Quale angolo il vettore accelerazione forma con
il vettore velocità all’istante t*?
44) Un punto materiale si muove su una circonferenza di raggio R = 50 cm con accelerazione angolare
costante α = π/2 rad/ s2 in senso antiorario. Il punto parte con velocità nulla dal punto A (fig. 2). Dopo quale
intervallo di tempo il punto ha percorso una semicirconferenza? Qual è il modulo della velocità e
dell’accelerazione in tale istante?
45) Un punto materiale si muove in senso orario su una circonferenza di raggio R = 1 m con legge oraria
θ(t) = bt2 + ct radianti
2
con b = 4 rad/s e c = 1 rad/s.
Calcolare il modulo della velocità e dell’ accelerazione nell’istante t = 1 s. Il punto parte con velocità nulla?
In quale istante il modulo dell’accelerazione tangenziale è uguale al modulo dell’accelerazione centripeta.
46) Un punto si muove su un piano e le equazioni orarie del suo moto sono:
x = b t4 metri
y = c t2 metri
4
2
dove b = 3 m/s e c = 2 m/s .
Calcolare il vettore posizione dopo 1 s (dare modulo e angolo con l’asse x) e il vettore velocità nell’istante 2
s. Calcolare il vettore accelerazione in funzione del tempo. Scrivere l’equazione della traiettoria.
47) Un punto materiale si muove su una circonferenza di raggio R = 1 m con legge oraria
θ(t) = bt2 + ct radianti
2
con b = 0.5 rad/s e c = 2 rad/s. Determinare la velocità angolare e l’accelerazione angolare in funzione del
tempo. Calcolare il vettore accelerazione all’istante t = 2 s.
48) All’istante t* un punto che si muove in verso antiorario su una circonferenza di raggio R = 2 m ha una
velocità v = 8 m/s e il vettore accelerazione diretto come in fig.1. Determinare l’accelerazione centripeta,
l’accelerazione tangenziale e il modulo dell’accelerazione (totale) nell’ l’istante t*. Supponendo
l’accelerazione tangenziale costante calcolare il numero di giri necessari al punto per fermarsi.
49) Un punto materiale P si muove su una circonferenza di raggio R = 1 m con velocità di modulo v(t) = bt2
con b = 3 m/s3. Il punto materiale si muove in verso antiorario e passa per A nell’istante t = 0 (fig. 2).
Trovare l’espressione in funzione del tempo a) delle coordinate cartesiane di P (rispetto agli assi cartesiani di
fig. 2); b) della velocità angolare, c) del vettore accelerazione.
fig.1
fig.2
fig. 3
50) Uno dei primi metodi per misurare la velocità della luce faceva uso di una ruota dentata. Mentre la ruota
è in rotazione un raggio di luce passa attraverso un intaglio, si riflette in uno specchio e ritorna passando
attraverso l’intaglio successivo. Se la ruota, con un raggio di 5 cm, ha 500 intagli sul bordo e lo specchio
dista 500 m dalla ruota, calcolare la velocità angolare (costante) della ruota; calcolare la velocità di un punto
del bordo. La velocità della luce è 3 x 108 m/s
R 3.8 x 103 rad/s; 190 m/s
51) La fig 3. rappresenta uno schema di trasmissione a cinghia. La ruota A di raggio 10cm è accoppiata
tramite la cinghia B alla ruota C di raggio 25 cm. Se la ruota C ha una velocità angolare di 100 giri/min
quale sarà la velocità angolare di A nel caso che la cinghia non slitti. (in assenza di slittamento le velocità
dei bordi delle due ruote sono uguali).
Moto armonico
1) Un pendolo di lunghezza l = 10 m viene lasciato quando forma un angolo di 5 ° con la verticale . Scrivere
l’equazione oraria del moto del pendolo.
2) Un pendolo ha un’equazione oraria θ(t) = 0.5 sen (π/2t)
Calcolare a) il periodo e la lunghezza. b) gli istanti in cui passa per la posizione di equilibrio; c) gli istanti in
cui raggiunge la massima elongazione
3) Un oscillatore armonico è costituito da una molla di costante elastica k = 100 n/m e un corpo di massa m
= 1 kg. Il corpo viene lasciato quando la molla è allungata di 20 cm. Scrivere l’equazione orario del moto
dell’oscillatore.
Composizione dei moti
4) Una barca che si muove con velocità v0 = 3 m/s rispetto all’acqua deve attraversare un fiume largo l = 1,8
km la cui corrente fluisce con velocità V = 2 m/s. Se la barca si muove perpendicolarmente alla corrente
calcolare la velocità della barca rispetto alla riva, il tempo per l’attraversamento e la distanza a valle del
punto di partenza in cui approda la barca.
5) Un ascensore si muove verticalmente con accelerazione a = 0.5 m/s2. Un passeggero di 70 kg è
nell’ascensore. Calcolare il suo peso apparente 1) quando l’accelerazione è verso l’alto, 2) quando è verso il
basso .R 721N, 651 N
6) Un aereo si sta muovendo verso est alla velocità di 200 km/h mentre un forte vento spira in direzione Sud
alla velocità di 65 km/h. Quale è la velocità dell’aereo rispetto al suolo in modulo e direzione. Se vuole
atterrare ad Est in quale direzione deve puntare il suo aereo.
R 210 km/h, 18° ES, 20° EN
Nota
Per θ << 1 radiante sen θ ≈ θ