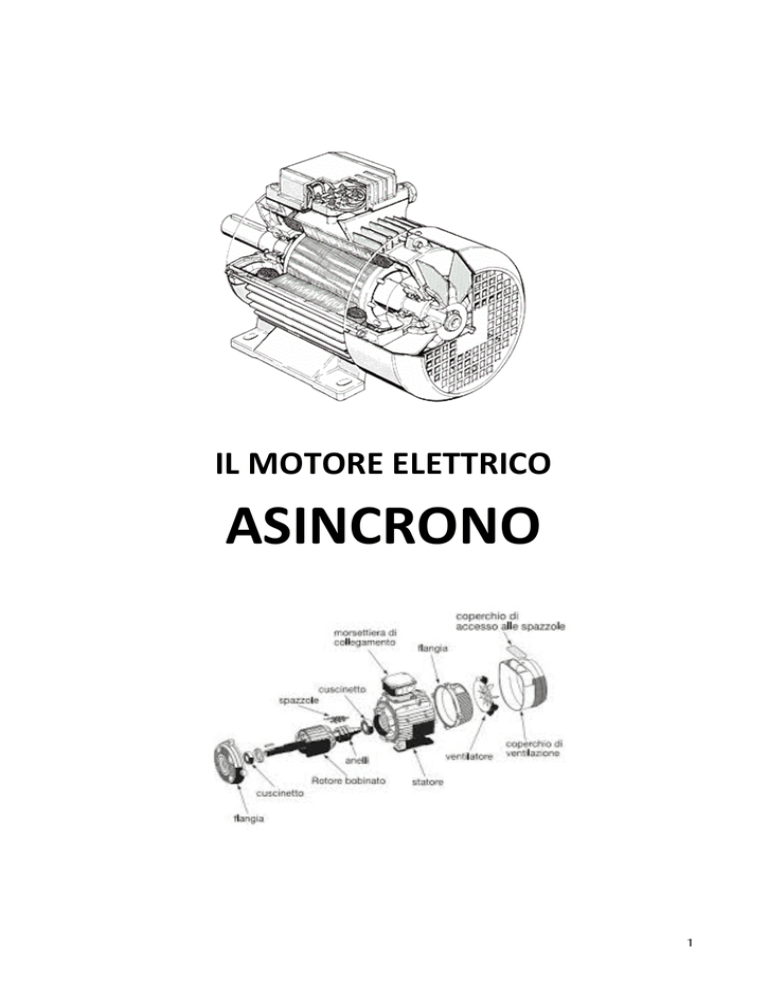
IL MOTORE ELETTRICO ASINCRONO 1 Motore Asincrono Trifase:
Il Motore Asincrono Trifase venne per la prima volta realizzato da Galileo Ferraris nel 1885. Esso viene alimentato direttamente dalla rete di distribuzione, a tensione e frequenza costanti, e rappresenta il motore elettrico più semplice, economico, robusto ed affidabile che la tecnica conosca. È ad elevato rendimento, non richiede lubrificazione, né manutenzione, non presenta alcuna difficoltà o particolarità per l’avviamento e, pertanto, è il dispositivo più diffuso nell’utilizzazione dell’energia elettrica come ‘forza motrice’. Il suo principio di funzionamento si basa sulla creazione di un campo magnetico rotante, realizzabile per mezzo di circuiti fissi nello spazio e percorsi da correnti polifasi, in particolare da correnti trifasi. Tuttavia, per piccole potenze, oppure per limitate applicazioni speciali, questo motore può anche essere di tipo monofase, come vedremo più in dettaglio nel seguito. Rispetto agli altri tipi di motori elettrici, presenta diversi vantaggi: peso ed ingombro ridotti a parità di potenza; mancanza di particolari dispositivi di eccitazione prelevando, direttamente dalla rete, la potenza magnetizzante necessaria per creare il flusso induttore della macchina; è autoavviante; sviluppa, spontaneamente ed automaticamente, variando la propria velocità, una coppia motrice atta a controbilanciare la coppia resistente applicata all’albero motore, determinando un funzionamento stabile (all’aumentare del carico rallenta); sovraccaricabilità, anche il 100% della sua potenza nominale; esigenze di manutenzione molto ridotte, semplicità di esercizio ed alto rendimento. Segue da quanto detto che, laddove un dispositivo meccanico deve essere azionato senza particolari esigenze di regolazione di velocità o di coppia, ivi è il regno incontrastato di 2 applicazione del MAT: montacarichi, gru, ascensori, macchine utensili tradizionali, pompe, ventilatori sono da decenni azionati in maniera soddisfacente da questo tipo di motore. Motore Asincrono Trifase:
Il principio di funzionamento di qualsiasi motore elettrico si basa sulle applicazioni delle azioni meccaniche (forze) che si esercitano tra elettromagneti e correnti. Come abbiamo già discusso nello studio della macchina sincrona, queste forze sollecitano i conduttori quando, immersi in un campo magnetico, sono percorsi da corrente. Nel caso particolare in cui il campo e la corrente siano perpendicolari tra loro, l’intensità di questa forza è data da F=iLB, e si misura in newton se l’induzione magnetica B è in tesla, la lunghezza L dei conduttori in metri e la corrente i in ampere. Il funzionamento del motore asincrono trifase si basa, inoltre, sull’impiego di un campo magnetico del tutto speciale, il campo magnetico rotante. Per rendere più concrete le idee, consideriamo una spira di materiale conduttore immersa in un campo magnetico rotante; la spira è imperniata e libera di ruotare intorno ad un asse, parallelo o coincidente con 3 l’asse di rotazione del campo rotante. Supponiamo che il campo magnetico del vettore induzione B sia uniforme e che tutte le linee di flusso costituiscano un complesso solidale rotante con velocità angolare ω intorno all’asse A -­‐‑ A'ʹ, in verso antiorario per chi guarda da A. Da quanto detto in precedenza, la spira sarà sede di fenomeni di induzione elettromagnetica, tranne nel caso in cui essa ruoti con la stessa velocità del campo. Nel caso in cui questa spira fosse ferma avremo che il flusso magnetico concatenato con essa risulterà essere, essendo il campo del vettore B uniforme e rotante con velocità ω0, variabile nel tempo con legge sinusoidale di pulsazione ω0. Questa variazione di flusso indurrà una f.e.m. (Forza Elettromotrice indotta) nella spira chiusa con conseguente circolazione di una corrente, anch’essa sinusoidale di pulsazione ω0, che, per la legge di Lenz, avrà un verso tale da opporsi alla causa che l’ha generata, cioè al moto relativo (rotatorio) fra campo magnetico e spira. La corrente indotta tenderà ad annullare, o, comunque, a ridurre l’entità di questo moto relativo, cioè, per effetto delle forze elettromagnetiche cui è soggetta la spira, tenderà a far ruotare la spira nello stesso verso del campo rotante: ecco dunque l’effetto motore Se però la spira ruotasse ‘sincrona’ con il campo rotante, cioè con la stessa velocità ω0, il moto relativo tra spira e campo si annullerebbe e si ridurrebbe a zero sia la f.e.m. indotta che la corrente nella spira, con la conseguente scomparsa delle forze elettromagnetiche. I ben noti fenomeni elettromagnetici che danno luogo a forze, e quindi a momenti di forze (o, se volete, a coppie meccaniche), allorché una corrente elettrica scorre in una spira immersa in un campo magnetico, hanno luogo, nel sistema considerato, solo se nella spira circola corrente. Questa corrente non può esistere che per ‘induzione’, la quale può sostenersi solo se la spira ruota in maniera ‘asincrona’ rispetto al campo rotante, cioè ruota con una velocità angolare diversa da ω0; da ciò nasce l’aggettivo ‘asincrono’ adoperato per 4 definire questo tipo di motore, che viene chiamato anche motore ‘a campo rotante’, perché è la più importante applicazione della scoperta di Ferraris; o ancora motore ad ‘induzione’ non tanto perché il fenomeno dell’induzione elettromagnetica sia fondamentale, come del resto è per tutte le macchine che sfruttano tale fenomeno, ma perché la parte rotante è sede esclusivamente di correnti indotte, indispensabili per il suo funzionamento. In pratica è come se si venissero a creare 2 campi magnetici rotanti: uno statorico ed uno rotorico. Quello rotorico insegue quello statorico senza mai raggiungerlo; se lo raggiungesse, le correnti rotoriche si annullerebbero e scomparirebbe il campo rotante generato dal rotore e con esso le azioni dinamiche (forze); in due parole: la coppia motrice si annullerebbe. Dunque, affinché esista coppia meccanica, la spira deve ruotare attorno all’asse A -­‐‑ A'ʹ con una velocità angolare diversa da ω0 (con ω0 > 0); indichiamo con ω, diversa da ω0, questa velocità angolare della spira. Risulta che, se 0 < ω < ω0, la coppia esercitata dalla spira è concorde con il verso di rotazione del campo magnetico e la macchina funziona da motore; se, invece, ω > ω0 la coppia esercitata è di segno discorde con il verso di rotazione del campo magnetico e la macchina funziona da generatore. 5 La spira segue, pertanto, la rotazione del campo magnetico ad una velocità minore in modo tale che scaturisca un moto relativo di scorrimento tra campo magnetico induttore e spira indotta ed in quest’ultima circolino correnti di intensità tale da sviluppare una coppia motrice capace di mantenere la spira in rotazione. Se la spira rallentasse per la presenza di una coppia frenante maggiore, aumenterebbe la velocità angolare con la quale il campo precede la spira, cioè aumenterebbero la differenza tra le due velocità e la f.e.m. indotta e, di conseguenza, le correnti e la coppia motrice assumerebbero un valore tale da vincere la nuova coppia resistente ad una diversa velocità. Ciò vuol dire che, in questo tipo di motore, una diminuzione della velocità comporta un automatico aumento della coppia motrice. Struttura generale
Il motore asincrono è costituito, come mostrato in Figura 3.3, da due parti fondamentali di forma cilindrica coassiali: una parte esterna, fissa, detta ‘statore’ ed una interna, coassiale, munita di albero, sostenuto da due supporti, libera di ruotare intorno all’asse della macchina, detta ‘rotore’. In particolare, nella figura si notano i seguenti dettagli:
1. albero con chiavetta;
2. anello della gabbia;
3. sbarra di rame;
4. morsettiera;
5. ventola di raffreddamento;
6. spaccato delle matasse degli avvolgimenti di statore;
7. spaccato del circuito magnetico statorico;
8. pacco del circuito magnetico rotorico;
9. alette di raffreddamento della carcassa esterna.
6 Statore
La realizzazione dello statore, detto anche induttore, dei MAT, sia per struttura magnetica che per formazione degli avvolgimenti, è del tutto identica a quella dello statore della macchina sincrona. Avremo quindi uno statore provvisto di avvolgimento trifase, eseguito con un certo numero “N” di coppie di poli (1 coppia polare, 2 coppie polari, ......n coppie polari), alimentato sempre da una linea trifase. La relazione che lega frequenza della corrente di alimentazione e numero di coppie polari alla velocità angolare (e quindi al num. di giri/minuto) del campo magnetico rotante (velocità di sincronismo) è la seguente: 𝑛! = 60 ∗ 𝑓𝑟𝑒𝑞.
𝑔𝑖𝑟𝑖
[
𝑚𝑖𝑛] 𝑁. 𝑐𝑜𝑝𝑝𝑖𝑒
Ora, essendo la frequenza f costante e pari a 50 Hz. un numero intero, il numero di giri al minuto n0 potrà assumere solamente certi valori che abbiamo riportato nella tabella seguente. E, poiché la velocità effettiva di rotazione di un motore asincrono è solo leggermente inferiore a quella di sincronismo, queste saranno le sole velocità possibili per un motore asincrono. N° n0 coppie polari [giri/min] 1 3000 2 1500 3 1000 4 750 5 600 7 I capi delle tre fasi, per poter collegare le fasi ultimate a stella o a triangolo, vengono riportati a sei morsetti situati sulla carcassa, risulta così comodo modificare le connessioni tra i morsetti, come illustrato in figura: Possiamo ora introdurre una variabile tipica di questo motore, lo scorrimento, che lega il numero di giri del rotore a quello di sincronismo del campo magnetico rotante. Allora prestiamo la massima attenzione alle definizioni di seguito elencate: •
n0
•
n
!"∗!"#$.
velocità di sincronismo 𝑛! = !.!"##$%
velocità effettiva del rotore 𝑛 [
𝑔𝑖𝑟𝑖
𝑚𝑖𝑛]
Introduciamo ora in concetto di “scorrimento” come il rapporto di seguito indicato: 𝑺𝑪𝑶𝑹𝑹𝑰𝑴𝑬𝑵𝑻𝑶 𝒔 = 𝒏𝟎 − 𝒏
𝒏𝟎
Ora, poiché la velocità del rotore può assumere qualsiasi valore, lo scorrimento potrà variare da più a meno infinito. In particolare, quando il rotore ruota alla velocità di sincronismo, n = n0, risulta s = 0; quando il rotore è fermo, cioè n = 0, si avrà, invece, s = 1. Rotore
La realizzazione del Rotore, dal punto di meccanico è costituita da un albero sorretto da due cuscinetti (schema statico: trave su 2 appoggi); il rotore ruota liberamente all’interno 8 dello statore. Il gioco tra esterno del rotore ed interno dello statore è costituito dallo spazio vuoto esistente tra i due elementi (uno fisso e l’altro mobile) ed è detto traferro. Dal punto di vista elettrico, il Rotore può essere realizzato in due modi diversi: •
ROTORE AVVOLTO: con un avvolgimento chiuso su se stesso in corto circuito
Nelle cave rotoriche delle macchine con rotore avvolto vi è un normale avvolgimento, simile a quello statorico, di tipo trifase e collegato a stella. •
ROTORE A GABBIA di scoiattolo: con una serie di barre di rame chiuse agli estremi con
due anelli anch’essi di rame.
9 Il rotore a gabbia dà luogo al più semplice e robusto dei motori asincroni: in ognuno dei canali, di rotore si infila una sbarra di rame, le cui testate, ad entrambe le terminazioni, vengono chiuse da un anello di rame. Il rotore ha così la forma di una gabbia e viene chiamato rotore a ‘gabbia di scoiattolo’ o ‘in corto circuito’. È evidente che questo circuito presenta resistenze bassissime e non ha un numero di poli propri, adeguandosi, in maniera naturale, al numero dei poli di statore, che può essere un numero qualsiasi. Le tensioni in gioco per ogni barra sono molto basse, dell’ordine di qualche volt, mentre le correnti, data la bassa resistenza, sono piuttosto elevate. Queste bassissime resistenze sono causa di inconvenienti all’atto dell’avviamento. Le correnti assorbite dallo statore in queste condizioni possono raggiungere 4 -­‐‑ 10 volte la corrente nominale, a seconda del tipo di rotore; questa corrente, tuttavia, è così sfasata, che la coppia di spunto, cioè la coppia necessaria ad avviare il motore, risulta essere particolarmente bassa. Caratteristica meccanica del motore asincrono
Nell’attimo iniziale dell’avviamento del motore, si ha la massima differenza tra la velocità di sincronismo del campo magnetico rotante statorico (n0) e la velocità del rotore (velocità del motore n=0: il motore è fermo !!!). In queste condizioni si sviluppa una coppia motrice che è funzione della corrente indotta nel rotore; pertanto possiamo anche dire che la coppia motrice iniziale (coppia di spunto) dipende in qualche modo dalla resistenza elettrica del rotore. Quando il motore non è collegato a nessuna utenza, esso non risulta frenato da niente ad esclusione dell’attrito interno dovuto ai cuscinetti e alla ventilazione interna. Si usa dire che il motore “gira a vuoto”. In queste condizioni il valore di “n” è praticamente quasi uguale a “n0”: velocità effettiva del motore circa uguale a quella di sincronismo. Ma come già indicato all’interno di questo documento, la quasi sincronia tra campo magnetico rotante generato dallo statore e quello indotto dal rotore annulla di fatto la coppia motrice. 10 L’andamento della coppia motrice esercitata dalle azioni (forze) elettriche tra campo magnetico rotante e circuiti elettrici rotorici segue l’andamento descritto i figura. Nella figura si può vedere come al variare della coppia resistente, il motore trova sempre il suo punto di equilibrio. Il punto B rappresenta la situazione in cui la coppia resistente è praticamente nulla (funzionamento a vuoto del motore). Mano a mano che al motore viene applicata una coppia resistente sempre maggiore il punto di equilibrio (e pertanto di funzionamento del motore) si sposterà da B verso A. Ciò dimostra la stabilità del motore asincrono: al crescere della coppia resistente, il motore asincrono rallenta ma non si ferma perché è in grado di generare una coppia motrice sempre maggiore e più grande della precedente. Si dice che il motore è stabile in quanto trova sempre un punto di equilibrio. Ciò è vero fino al punto massimo della curva della coppia (punto A). Nel punto A (massimo della curva) si ha il funzionamento critico del motore: se la curva resistente cresce ancora, il motore rallenta, ma la coppia corrispondente (a sinistra del punto “A”) è più bassa e pertanto il motore in breve si fermerà. In poco parole la zona stabile del motore è quella alla destra del punto “A” fino al punto “B”. 11 Vediamo ora la problematica dell’avviamento di un motore asincrono “sotto carico” anziché a vuoto, cioè di come far partire un motore asincrono anche se in fase di spunto abbiamo una coppia resistente “importante”. La fase di avviamento di un motore consiste nel portare la velocità del motore da zero a quella nominale. Affinché il motore possa avviarsi ed accelerare, è necessario che la coppia di spunto sia superiore alla coppia resistente del carico, sempre all’avviamento,. Inizialmente il rotore è fermo e lo statore non alimentato; la tensione e la frequenza nominali del motore sono uguali a quelli della linea di alimentazione. Quando si chiude l’interruttore che collega la linea al motore (rotore fermo, n=0 e s = 1) questo si comporta come un trasformatore chiuso in cortocircuito e nel primo istante di avviamento, come più volte ribadito, assorbe dalla linea la massima corrente, così elevata (4 ÷ 8 volte la corrente nominale) che può dar luogo a diversi inconvenienti, tra i quali un eccessivo riscaldamento degli avvolgimenti e della linea, se l’avviamento è lento, ad un’elevata caduta di tensione lungo la linea, con problemi agli utilizzatori se questi sono particolarmente sensibili alla tensione, e, se anche l’avviamento fosse rapido, un intempestivo intervento delle protezioni sulla linea. Si accennerà ora agli accorgimenti usati per ovviare a questi inconvenienti. 1. Cspunto > CResistente
Coppia di spunto erogabile dal motore asincrono (curva in
rosso), maggiore della coppia resistente (curva in nero) applicata al motore in fase di
avviamento.
2.
Dalla figura si può vedere che con questa
situazione il motore è perfettamente in grado di
avviarsi da solo, senza nessun problema; dopo un
transitorio iniziale, il motore girerà a n giri/min.
3. Cspunto < CResistente Coppia di spunto erogabile dal motore asincrono, minore della
coppia resistente applicata al motore in fase di avviamento.
Dalla figura si può vedere che con questa situazione il
motore non è in grado di avviarsi da solo; il rotore
risulterebbe “bloccato”.
12 Per sopperire ai problemi di avviamento, si ricorre all’attuazione di una delle due strategie di seguito illustrate: •
•
•
Avviamento con la commutazione stella/triangolo
Avviamento con Reostato (resistenze elettriche esterne collegate agli
avvolgimenti rotorici; è fattibile solo con rotore avvolto.
Rotore a DOPPIA GABBIA
L’avviamento stella-­‐‑triangolo, mostrato in figura, viene utilizzato per quei motori la cui tensione nominale, per ciascuno dei suoi avvolgimenti statorici, sia uguale alla tensione concatenata della linea di alimentazione (in genere 400 volt). 2
Collegam. a STELLA : V = 230 Volt = 400/ 3 Collegam. a TRIANGOLO : V = 400 Volt All’avviamento le fasi del motore vengono collegate a stella; durante la marcia normale vengono invece commutate a triangolo. All’avviamento gli avvolgimenti statorici, collegati 2
a stella, saranno soggetti ad una tensione ridotta 3 volte, la corrente di linea assorbita dal motore si riduce di un terzo come pure la coppia di spunto, proporzionale al quadrato della tensione. Questo metodo, molto usato in passato, ha però l’inconveniente di presentare un brusco aumento della corrente e della coppia nel passaggio da stella a triangolo. 13 Se il motore è a rotore avvolto, sarà dotato di anelli, spazzole e di un collegamento resistenze variabili esterne, ma sempre facenti parte del circuito di rotore. Come mostrato in figura, i capi di queste fasi vengono collegati a degli anelli conduttori, calettati sull’albero del motore ma isolati da questo, sui quali poggiano delle spazzole collegate ad un reostato esterno di avviamento, completamente inserito all’atto di chiusura dell’interruttore sulla linea, ma che va disinserito, gradualmente, all’aumento della velocità di rotazione e completamente escluso, cortocircuitato, in condizioni di normale funzionamento. Questa terna di resistenze è chiamata reostato d’avviamento ed avviamento reostatico il tipo di avviamento per tali motori. La presenza di una elevata resistenza rotorica all’atto dell’avviamento e con tensione di alimentazione costante, ha un duplice scopo: da un lato l’impedenza rotorica 14 aumenta di modulo con una conseguente diminuzione della corrente assorbita dal motore all’avviamento; dall’altro l’aumento della resistenza comporta una diminuzione dello sfasamento delle correnti rotoriche con conseguente aumento del valore della coppia di avviamento e quindi dell’accelerazione. Dal punto di vista elettrotecnico, la relazione matematica che lega la copia motrice alle variabile elettriche è la seguente: 𝐶!"#$%& = 𝑘 𝑉 !
𝑅! 𝑠
!
!
𝑅! + 𝑋
dove: V = tensione di alimentazione Rr = resistenza rotorica s = scorrimento = 𝒏𝟎 !𝒏
𝒏𝟎
= 𝝎𝟎 ! 𝝎
𝝎𝟎
X = reattanza di dispersione rotorica Ricordando che l’induttanza rotorica è pari a: 𝐿! = 𝐿∗! + 𝐿!" Ricordando altresì che la reattanza rotorica è pari a: 𝑋 = 𝜔 𝐿!" = 𝑠𝜔! 𝐿!" si ha: 𝐶!"#$%&' = 𝑘 𝑉 !
𝑅! 𝑠
𝑅!! + 𝑠 ! (𝜔0 𝐿𝑟𝑑 )! scorrrimento S = 1 smax s = 0 15 Si può dimostrare che lo scorrimento nel punto di coppia massima è pari a: 𝑠!"# =
𝑅! 𝜔! 𝐿!" Se io voglio spostare smax più a sinistra verso l’origine (vedere figura), io dovrò aumentare il suo valore e pertanto dovrò aumentare la resistenza rotorica Rr. aggiungere resistenze rotoriche si può fare solo con rotori avvolti e necessita di contatti striscianti (anelli e spazzole). Con il rotore a doppia gabbia si vengono a creare due circuiti elettrici: un circuito più esterno, a sezione ridotta (realizzato a volte anche in metallo diverso: ottone, alluminio) ed un circuito più interno e profondo a sezione maggiore e generalmente realizzato in rame. La sezione della “doppia gabbia” a volte può avere forme diverse (a; b; c; .....) come raffigurato in figura. A causa del diverso valore del flusso concatenato, i due circuiti avranno un valore della resistenza ed in particolare della impedenza diverso tra loro. Più dettagliatamente si può dimostrare che la gabbia esterna (a sezione minore) avrà un valore della resistenza maggiore ma un valore della reattanza di dispersione minore perché non è immersa completamente nel ferro; viceversa, la gabbia interna (a sezione maggiore) avrà un valore della resistenza minore ma un valore della reattanza di dispersione maggiore. Resistenza rotorica: Rr con Re > Ri Reattanza di dispersione: 𝑋 = 𝜔 𝐿!" con 𝐿!" > 𝐿!" In pratica si gioca sul diverso valore dell’impedenza Z al variare del numero di giri: 𝑍! =
2
𝑅!! + 𝑠 ! 𝜔!! 𝐿!!" 𝑍! =
2
𝑅!! + 𝑠 ! 𝜔!! 𝐿!!" 16 Al crescere del numero di giri, quindi al diminuire dello scorrimento “s” l’impedenza Ze cresce e Zi diminuisce; ciò fa si che all’avviamento Ze < Zi mentre a regime Ze > Zi . Poiché la corrente va sempre dove l’impedenza è minore, all’avviamento la corrente (generalmente elevata) tenderà a transitare nella gabbia esterna a impedenza minore, e in marcia normale la corrente (ormai diminuita ai valori nominali) tenderà a transitare nella gabbia interna. In sintesi: le correnti allo spunto andranno nella gabbia esterna ad impedenza minore ma a resistenza maggiore; è come se noi avessimo messo delle resistenze rotoriche aggiuntive !!! Il risultato è quello di avere all’avviamento una coppia più elevata. Nella figura si nota a destra la curva della coppia di un motore a semplice gabbia, mentre a sinistra è rappresentata la coppia di un motore a doppia gabbia. 17 Motore asincrono a giri variabili
Nell’attimo iniziale dell’avviamento del motore, si ha la massima differenza tra la velocità Come abbiamo avuto modo di sottolineare, il MAT presenta innegabili vantaggi; tuttavia presenta la caratteristica di conservare pressoché costante la velocità al variare del carico. In molti casi occorre variare la velocità del motore in un ampio campo con un determinato valore di momento motore (regolazione a coppia costante) oppure con una coppia inversamente proporzionale alla velocità (regolazione a potenza costante). La velocità effettiva del motore asincrono è pari a 60 𝑓𝑟𝑒𝑞.
𝑛 = ∗
𝑁!"##$%
1 − 𝑠 per cui, per variare la velocità di un motore asincrono, occorrerà variare o lo scorrimento, o il numero delle coppie polari, o la frequenza della linea di alimentazione. Oggi, grazie all’elettronica di potenza, la variazione della frequenza è praticamente la soluzione più conveniente. La rete di distribuzione è a frequenza fissa, per cui per avere una sorgente a frequenza variabile si ha la necessità di un convertitore di frequenza, come indicato in Figura, chiamato INVERTER. In pratica l’inverter all’ingresso presenta la corrente di alimentazione “standard” (corrente trifase 400 Volt e 50 Hz); all’uscita la corrente risulterà modificata sia come tensione che come frequenza. Oggi esistono in commercio INVERTER regolabili in grado di geerare frequenze e tensioni variabili. Di seguito si riportano gli andamenti della coppia in funzione di frequenze e tensioni variabili. 18 È da tener presente che frequenza, tensione e flusso sono legati dalla relazione approssimata V ≅ k f Φ Da ciò segue che si potranno verificare due casi. a) Diminuzione della frequenza nominale e della velocità Questo comporta la
contestuale diminuzione della tensione di alimentazione, in modo tale da far
rimanere il flusso costante. Un suo aumento comporterebbe problemi di saturazione
del nucleo, aumento della corrente magnetizzante e delle perdite nel ferro.
19 b) Aumento della frequenza nominale e della velocità Si preferisce, in questo caso,
mantenere costante la tensione di alimentazione, con conseguente diminuzione del
flusso, questo per compensare l’aumento delle perdite nel ferro dovute all’aumento
della frequenza (ricordate che le perdite per correnti parassite sono proporzionali al
quadrato della frequenza, mentre quelle per isteresi sono direttamente proporzionali
alla frequenza).
Dati di targa
Ogni motore asincrono, così come prescrivono le norme CEI, deve essere munito di una targa che indichi i valori nominali delle grandezze elettriche e meccaniche essenziali per la specificazione della macchina stessa. In tale targa vengono indicati tra l’altro: a) la tensione nominale che rappresenta la tensione concatenata di alimentazione
statorica per la quale il motore è stato dimensionato;
b) la frequenza nominale, che è la frequenza della rete di alimentazione;
c) la velocità nominale, cioè la velocità di rotazione, in giri al minuto, del motore in
condizioni nominali;
d) la potenza nominale, ossia il valore della potenza meccanica, espresso in chilowatt,
disponibile sull’asse del motore in condizioni nominali, cioè a tensione, frequenza e
velocità nominali;
e) la corrente nominale, cioè il valore della corrente assorbita dalla linea, per ogni fase
statorica, in condizioni nominali;
f) il fattore di potenza nominale, che rappresenta il coseno dell’angolo di sfasamento
tra tensione e corrente, di ogni fase statorica, in condizioni nominali;
g) il rendimento nominale, cioè il valore del rendimento in condizioni nominali; - la
coppia nominale, cioè il valore della coppia motrice, in [N m], sull’albero motore in
condizioni nominali;
h) il numero dei poli del campo magnetico di statore.
Vengono inoltre riportate altre informazioni come l’indicazione della casa costruttrice, il tipo di motore, il collegamento delle fasi, la classe d’isolamento, il grado di protezione IP (che indica il grado di protezione contro l’ingresso di sostanze solide, liquide ed aeriformi) dell’involucro. Inoltre, se il rotore è avvolto, compaiono anche la tensione e la corrente di rotore che si hanno allo spunto con resistenza di avviamento avente valore tale che la corrente di statore sia uguale a quella nominale, mentre, se il rotore è a gabbia, non vengono riportati i dati relativi al rotore. Motore asincrono monofase
In alcuni casi l’indisponibilità di una linea trifase rende necessario l’utilizzo di motori asincroni monofasi, detti anche motori monofasi ad induzione, utilizzati per potenze modeste, fino ad alcuni chilowatt, come elettrodomestici, pompe, ventilatori. Questi motori sono costruttivamente simili a quelli trifasi, anche se a parità di dimensioni e di velocità, presentano una potenza ridotta della metà, con l’avvolgimento statorico monofase e quello rotorico generalmente a gabbia. 20 L’avvolgimento statorico, che generalmente occupa i due terzi della periferia statorica ed è alimentato con una tensione sinusoidale, è percorso da una corrente che dà luogo ad una f.m.m. anch’essa alternativa sinusoidale. Al traferro avremo, quindi, un campo magnetico alternativo, cioè fisso nello spazio e di ampiezza variabile sinusoidalmente come la corrente. In forza del cosiddetto teorema di Leblanc, un campo alternativo può considerarsi ottenuto dalla sovrapposizione di due campi magnetici aventi ugual valore costante, pari alla metà di quello massimo del campo alternativo, e rotanti con velocità angolari uguali ed opposte, pari proprio alla pulsazione della corrente statorica (con una coppia di poli). Ciascuno di questi campi produce gli stessi effetti che abbiamo visto per il motore trifase e, pertanto, si può ripetere quanto già detto per tale motore, cioè che ciascuno dei due campi magnetici rotanti, considerato singolarmente, sostiene f.e.m. e correnti nella gabbia rotorica. Questi due campi rotanti, sommati con quelli originati dallo statore, danno luogo al campo magnetico rotante risultante nel traferro. Dall’azione tra campi magnetici e correnti indotte si originano due coppie motrici, uguali ed opposte, per cui se il rotore è fermo, esse si equilibrano a vicenda ed il motore non parte; se però avviamo il motore, anche con una spinta, in un verso qualsiasi, il motore continuerà a ruotare in tale verso, accelerando e raggiungendo una velocità prossima a quella di sincronismo. Ciò è dovuto al fatto che la coppia dovuta al campo che ruota nello stesso senso del rotore (campo diretto) diventa maggiore rispetto alla coppia dovuta all’altro (campo inverso) e nasce quindi una coppia risultante con un verso pari a quello del rotore. Ne deriva che il motore asincrono monofase non ha un suo senso di rotazione, ma assume quello che gli viene impresso. I diversi valori di coppia motrice che si hanno quando il motore ruota in un certo verso sono dovuti ai diversi valori dello scorrimento rispetto ai due campi rotanti, diretto ed inverso. Posto, con evidente significato dei simboli usati, 𝒔𝑫 = 𝒏𝟎 !𝒏
𝒏𝟎
𝒔𝑰 = 𝒏𝟎 ! !𝒏
𝒏𝟎
𝒏
= 𝟏 + 𝒏𝟎
si ha immediatamente che sD + sI = 2 . Allora, quando il rotore è fermo n = 0, risulta sD = sI = 1; quando, invece, il rotore ruota a velocità di sincronismo nel verso diretto, n = n0, si ha sD = 0 e sI = 2. Possiamo quindi affermare che quando lo scorrimento del campo diretto varia da 1 a 0, quello del campo inverso passa da 1 a 2. 21 Il diagramma risultante, mostrato in figura, da cui risulta che la coppia è pari a zero non solo a velocità di sincronismo ma anche a rotore fermo. Dalla figura si può, inoltre, osservare che il motore asincrono monofase funziona, rispetto a quello trifase, con uno scorrimento maggiore, la prima parte della caratteristica è meno ripida, quindi con rendimento e fattore di potenza più bassi. Per quanto detto, se non si adotta qualche accorgimento, il motore asincrono monofase non parte. Un accorgimento potrebbe essere quello di dotare lo statore di due avvolgimenti, sfasati di π/2, uno permanentemente inserito, detto avvolgimento principale o di lavoro, l’altro, detto avvolgimento ausiliario o di avviamento, che può rimanere oppure non rimanere inserito dopo l’avviamento e percorsi da correnti sfasate di π/2 in modo da creare un campo rotante bifase. In generale, queste condizioni non vengono mai soddisfatte per cui nel motore asincrono monofase non si avrà quasi mai un campo magnetico rotante perfetto, circolare, ma un campo di ampiezza non costante, ellittico, in grado comunque di avviare il motore. Il disinserimento dell’avvolgimento ausiliario avviene tramite un interruttore centrifugo che interviene generalmente ai tre quarti della velocità di sincronismo. Inoltre, l’avvolgimento ausiliario può essere attraversato da notevoli correnti, dato il breve lasso di tempo di funzionamento, per avere coppie di spunto elevate. Si possono usare vari tipi di avviamento per motori asincroni monofasi, sempre e solo di piccola potenza. In particolare i due avvolgimenti, dovendo essere alimentati alla stessa tensione per avere le due correnti sfasate tra loro di circa π/2, dovranno presentare impedenze diverse; uno dei modi semplici e più diffusi è quello di usare un condensatore (avremo il motore a condensatore). Il motore a condensatore può essere di due tipi. Il primo tipo è con condensatore permanentemente inserito ed è mostrato nella figura seguente: 22 Il secondo tipo è quello in cui il condensatore può essere inserito e disinserito, come suggerito nella seguente figura: Questi motori presentano notevoli coppie di spunto ed un fattore di potenza particolarmente elevato. Inoltre, possono presentare anche un doppio condensatore, uno permanentemente inserito, quindi notevolmente robusto, e l’altro solo in avviamento, di tipo elettrolitico, più economico. Nelle pagine seguenti 8in Appendice) sono raccolte alcune informazioni su argomenti di fisica e di elettrotecnica la cui conoscenza si ritiene indispensabile e va a costituire il bagaglio di “prerequisiti” necessario ed indispensabile per la comprensione del presente documento. 23 Ripasso di Fisica: CAMPO MAGNETICO
Il campo magnetico è un campo vettoriale: associa, cioè, ad ogni punto nello spazio un vettore, eventualmente
variabile nel tempo, il cui effetto fisico si esplica in termini della forza di Lorentz subita da una carica elettrica in
movimento oppure nel momento torcente che agisce su un dipolo magnetico. Le sorgenti del campo magnetico sono le
correnti elettriche oppure i dipoli magnetici.
Con il termine induzione magnetica (densità di flusso magnetico nel SI) si indica un fenomeno per cui un corpo,
sottoposto all'azione di un campo magnetico, si magnetizza a sua volta.
H = campo magnetico
B = densità di flusso magnetico o induzione magnetica
B=μH
dove μ è il coefficiente di permeabilità magnetica
L'unità di misura dell'induzione magnetica B nel SI è il tesla (T), mentre per H si usa l'ampere per metro (A/m)
La magnetizzazione può essere temporanea se, dopo poco, il corpo perde le caratteristiche di calamita; oppure può
essere permanente, se il corpo conserverà molto a lungo la sua magnetizzazione.
L'intensità di tale fenomeno è quantificata tramite l'omonimo vettore induzione magnetica (il cui modulo è misurato in
weber/m2 o anche in tesla) che, più in generale, dà conto delle azioni che un campo magnetico esercita sul sistema fisico
in cui si trova (per esempio un circuito percorso da corrente, ovvero da cariche elettriche in movimento).
Forza di un campo magnetico su un circuito La forza di Lorentz costituisce l'ʹeffetto del campo magnetico su corpi carichi in movimento: supponiamo che
che sarebbe la forza del campo elettrico sia pari a zero;
× indica il prodotto vettoriale, q è la carica elettrica, e v la velocità della carica.
24 Esempi di campo magnetico 1) Filo rettilineo infinito ……………….regola della mano destra e del pollice: 25 2) Spira circolare Vogliamo calcolare il campo magnetico sull'ʹasse di una spira di raggio R ……………….regola della mano destra e del pollice 26 3) Solenoide Il solenoide di lunghezza L può essere considerato un insieme di N spire coassiali di raggio R. Il campo magnetico ha la direzione dell'ʹasse del solenoide. dove n, chiamata densità di spire, è uguale al rapporto tra N e L, e C è una qualsiasi linea chiusa concatenante la
corrente I su tutte le spire (cioè N volte):
Flusso magnetico attraverso una superficie Superficie perpendicolare Se la superficie è piana e perpendicolare alla direzione del campo magnetico, la formula precedente si semplifica in
dove B è il modulo dell'induzione ed A l'area della superficie.
27 Campo magnetico omogeneo Per un campo magnetico omogeneo, cioè costante lungo tutti i punti di una superficie piana, il flusso magnetico
corrisponde al prodotto scalare dell'induzione magnetica
per la normale alla superficie
:
essendo α l'angolo compreso fra
ed
28 Circuiti ideali in regime sinusoidale
Si considerano, in questa parte, i circuiti con parametri ideali, utile premessa alla
successiva rappresentazione che terrà conto della effettiva costituzione circuitale.
Si analizzano i comportamenti in regime sinusoidale di una resistenza pura, di
un’induttanza pura e di una capacità pura.
Circuito con resistenza pura R
Figura: Resistenza pura alimentata da una sorgente in c.a. : valori efficaci, coincidenti, della tensione
applicata U e della caduta di tensione UR ai capi della resistenza.
Se si applica agli estremi di una resistenza R la d.d.p. sinusoidale di equazione
la corrente che percorre la resistenza seguirà le vicende della tensione, risultando quindi in
fase con essa e con ampiezza calcolata in ogni istante dalla legge di Ohm, ovvero dal rapporto fra il
valore della tensione e della resistenza in esame:
Passando ai valori efficaci della tensione e della corrente si scrive
29 Alle grandezze sinusoidali si associano i vettori i quali, per quanto è già stato detto,
generalmente hanno come modulo il valore efficace (e non il valore massimo), che viene indicato
con la lettera maiuscola.
Figura Diagrammi vettoriale e temporale della tensione applicata e della corrente che percorre una resistenza pura.
Circuito con induttanza pura L
Applicando ai capi della bobina pura (priva di resistenza e con induttanza costante) una
tensione sinusoidale, anche la corrente che l’attraversa è sinusoidale, ma le loro condizioni di fase e
le loro ampiezze sono di tipo particolare.
figura: Circuito puramente induttivo
Si parta dal presupposto che la corrente che attraversa la bobina sia sinusoidale, con
equazione temporale
Si vuole determinare la tensione da applicare ai capi della bobina in modo che vi circoli la
corrente (1).
Una corrente variabile crea un flusso variabile, legati dalla relazione
30 La variazione del flusso concatenato fa nascere, per la legge dell’induzione
elettromagnetica, una f.e.m. indotta che ostacola le variazioni della corrente:
Dalla trigonometria, essendo
la (3) si può scrivere
Associando la f.e.m.i. (4) ad un vettore, questo si troverà in ritardo rispetto al vettore
corrente, associato a sua volta alla corrente espressa dalla (1).
Nel circuito elementare formato dal generatore che produce una tensione sinusoidale u(t)
e dalla bobina pura ai cui capi è presente la f.e.m.i. data dalla (3), applicando il secondo principio di
Kirchhoff alla maglia si ha, trascurando la resistenza dell’avvolgimento e quindi la c.d.t. relativa:
il cui il valore massimo o ampiezza è
Passando ai valori efficaci
Si ricordino infatti le relazioni, fra i moduli , che legano valore efficace e massimo in regime sinusoidale:
Per la (6) la tensione U deve quindi controbilanciare la –E .
31 La tensione U fornita dal generatore, tenendo conto della sua posizione nel piano di Gauss
come evidenzia la fase della (5) si può scrivere, in valore efficace e per le note considerazioni
sull’operatore ‘j’ citate in precedenza:
Il vettore tensione U, per la (5) e per la (7), è dunque in anticipo rispetto alla corrente,
proprio perché deve essere opposto al vettore f.e.m.+E.
Definendo in particolare come reattanza induttiva XL il prodotto
la caduta di tensione ai capi della bobina ideale si scrive:
In altro modo si può osservare che il prodotto XLI ha le dimensioni di una c.d.t., in cui
l’ostacolo è la reattanza induttiva XL percorsa dalla corrente.
Questa “resistenza” particolare è in realtà un ostacolo che, percorso da corrente, crea ai capi
della bobina ideale una caduta di tensione che anticipa di 90° la posizione del vettore corrente.
Se si ricorda infatti il carattere inerziale della induttanza, ovvero della grandezza che
ostacola le variazioni di corrente, questo ostacolo viene attribuito alla reattanza, che congloba,
oltre alla induttanza, anche la frequenza.
Infatti con più rapide variazioni della corrente aumenta la difficoltà da parte della corrente
a percorrere il circuito induttivo.
In particolare con frequenza nulla è nulla anche la reattanza, mentre con frequenza
crescente cresce linearmente anche la reattanza, fino a diventare infinita con frequenza infinita.
- In corrente continua (f=0) la reattanza è un corto circuito;
- con frequenza infinita la reattanza è come un interruttore aperto.
Si conclude ricordando che a regime (esaurita quindi la fase transitoria il cui studio non è
qui riportato) una induttanza ha la proprietà di ritardare di 90° la corrente che l’attraversa rispetto
alla caduta di tensione esistente ai suoi capi.
32 In modulo e in valore efficace tale corrente è il rapporto fra la tensione efficace ai suoi
capi e la reattanza induttiva XL=ωL .
Alla reattanza induttiva si attribuisce quindi la scrittura
utile nelle applicazioni con il metodo simbolico.
Figura Diagrammi vettoriale e temporale riferiti ad un circuito puramente induttivo in regime
sinusoidale.
Circuito con capacità pura C
Figura Errore. Il segnalibro non è definito.) Circuito puramente capacitivo
Si prende ora in esame un condensatore ideale (trascurandone quindi eventuali effetti
resistivi dovuti alle perdite nel dielettrico e induttivi, di per sé già trascurabili) ai capi del quale si
imprime una tensione sinusoidale
33 Si ricorda che, quando si applica una tensione ai capi di un condensatore inizialmente
scarico, si ha un movimento immediato degli elettroni dall’armatura resa positiva dal generatore
fino a raggiungere l’altra armatura che acquista così il potenziale negativo.
Ad esempio nel processo di carica di un condensatore alimentato da una tensione continua, poniamo di 10V,
immediatamente gli elettroni migrano dall’armatura positiva verso quella negativa e il processo di migrazione continua fino alla
carica completa del condensatore, cioè quando fra le armature si stabilisce una d.d.p. praticamente uguale alla f.e.m. del generatore.
Durante la carica il processo di migrazione viene rallentato dal potenziale che man mano cresce ai capi del condensatore stesso.
Qui non si considera la fase transitoria e si ragiona come se essa si fosse già esaurita.
Se la tensione alternata ai capi del condensatore varia secondo la (8), in modo sinusoidale, il
legame fra la variazione di tensione, la variazione di carica e la corrente di spostamento vale,
essendo
q=ic ּ◌t=C ּ◌uc:
Pertanto la corrente che interessa il circuito formato dal generatore, dal condensatore e dai
collegamenti (di resistenza trascurabile anch’essi) si calcola, dalla (9) e tenendo conto della (8):
Ricorda che
Dalla (10) si deduce che la tensione impressa ai capi del condensatore e la corrente
che interessa il circuito capacitivo puro sono a 90° fra loro: la tensione è in ritardo rispetto alla
corrente (è lo stesso dire che la corrente anticipa la tensione impressa di 90°).
34 Figura: Diagrammi vettoriale e temporale riferiti ad un circuito puramente capacitivo alimentato con
tensione sinusoidale.
Dall’andamento temporale della tensione e della corrente a regime in un circuito
capacitivo puro (fig.6) si osserva che:
•
quando il condensatore è scarico (uc=0) in quell’istante la corrente è massima;
•
quando la tensione comincia a crescere si ha la carica del condensatore;
•
il condensatore è carico quando la tensione ai capi è massima (corrente nulla);
•
nell’intervallo di scarica la tensione ai capi diminuisce passando dal valore massimo a
zero, mentre la corrente cresce da zero al valore massimo;
•
nel semiperiodo negativo della tensione si ripetono l’analoga fase di carica e di
scarica.
•
Con tensione decrescente la corrente aumenta e viceversa con tensione crescente.
Si riprende in esame la (10).
L’ampiezza della corrente (il valore massimo) è:
Passando ai valori efficaci e definendo la reattanza capacitiva
35 dalla (11) si ottiene la relazione fra i moduli della tensione e della corrente in un circuito
puramente capacitivo:
La reattanza capacitiva Xc torna utile per considerare l’ostacolo che il condensatore offre
al movimento delle cariche. Essa ha qui la proprietà di creare una speciale c.d.t. ai capi del
condensatore percorso da corrente, speciale nel senso che è sfasata in ritardo di 90° rispetto alla
corrente (oppure, ovviamente, la corrente è in anticipo di 90° rispetto alla c.d.t. ai capi del
condensatore stesso).
Pertanto alla reattanza capacitiva, nel calcolo con metodo simbolico, si attribuisce l’una o
l’altra delle espressioni equivalenti
La (13) quindi va scritta con la seguente rappresentazione simbolica:
ovvero per rappresentare la c.d.t. ai capi del condensatore, legata alla corrente circolante:
La reattanza capacitiva decresce dal valore teorico infinito con frequenza nulla (ad
esempio in corrente continua, per f=0, cessato il transitorio di carica, non vi può essere ulteriore
movimento di cariche).
Al crescere della frequenza la reattanza diminuisce sempre più fino ad annullarsi con
frequenze altissime. Pertanto si può semplicemente affermare che
un condensatore con frequenze altissime si comporta come un corto circuito;
con frequenza nulla si comporta come un interruttore aperto.
36 Da ricordare
Vi è dualità fra:
- il circuito induttivo puro in cui l’induttanza L ostacola le variazioni di corrente (questo
può servire a ricordare che la corrente è in ritardo di 90° rispetto alla tensione impressa ai suoi capi)
e
- il circuito con capacità pura C, che ostacola le variazioni di tensione : si ricorda così
che la tensione ai capi ritarda di 90° la corrente (o che la corrente anticipa l’andamento della
tensione di 90°).
Il perché lo sfasamento sia di 90° è dimostrabile col calcolo differenziale.
Osservazione importante
In seguito, nei calcoli e nelle rappresentazioni con i vettori associati a grandezze
sinusoidali, non si farà più riferimento all’ampiezza del vettore, ma si intenderà rappresentarne il
valore efficace, che è quello comunemente sottinteso nelle applicazioni.
Quando si parla di una corrente di 2A o di una tensione di 230V ci si riferisce infatti al
valore efficace della grandezza in esame e pertanto anche il vettore che la rappresenta avrà il
modulo coincidente con il valore efficace, anziché col valore massimo.
Le grandezze suddette sono ritenute sinusoidali: la quasi totalità dell’energia elettrica è
prodotta e distribuita con questo andamento temporale (salvo poi eventualmente convertirla in
continua).
Si osserva ancora che, nelle rappresentazioni vettoriali e nelle equazioni, il vettore potrà
essere espresso con la lettera che lo rappresenta, sormontata dalla tipica frecciolina, come nelle
equazioni di fig. 7, oppure da una lineetta al posto della freccia, o la scritta in grassetto:
Più spesso si ricorrerà alla scrittura in grassetto.
Addirittura nei diagrammi vettoriali si intenderà che le grandezze presenti siano, appunto,
dei vettori.
Nel prossimo paragrafo si generalizzerà il concetto di ostacolo al passaggio della corrente,
mediante l’introduzione della impedenza Z.
37 Elementi passivi puri: schemi, diagrammi corrente-tensione
Nella fig.7 si riassumono le caratteristiche fondamentali dei circuiti semplici, con
riferimento agli sfasamenti fra la corrente che li attraversa e la corrispondente caduta di tensione ai
loro capi.
Figura: Schemi, rappresentazioni vettoriali ed equazioni riferite agli elementi passivi puri R - L - C.
Negli schemi e nei diagrammi si farà riferimento ai valori efficaci di tensione e di corrente in gioco. L’ostacolo al
passaggio della corrente in alternata è l’impedenza Z
38 Circuiti reali in regime sinusoidale - Impedenza
Circuiti reali in regime sinusoidale -­‐‑ Impedenza Nella parte precedente si sono visti i circuiti ideali, cosiddetti puri, cioè formati da una sola componente. Tuttavia un qualsiasi conduttore ha la propria resistenza e la corrente che lo percorre produce un flusso che gli si concatena, con relativa induttanza; inoltre la vicinanza di altri conduttori giustifica una capacità. Le grandezze citate sono distribuite lungo esso, ma per semplicità di calcolo i parametri vengono concentrati in un elemento resistivo, in uno induttivo e in uno capacitivo. Nei circuiti reali i parametri presenti negli schemi che si studiano sono quindi individualmente ideali, cioè sono parametri concentrati, ma tutti insieme contribuiscono a far sì che il circuito in questione tenga conto della propria effettiva costituzione. L’elemento assente viene quindi ritenuto nullo o comunque trascurabile nei limiti delle approssimazioni che si stanno considerando, rispetto agli altri parametri presenti. Ideali si ritengono i collegamenti dei conduttori tra i suddetti parametri. Ad esempio quando si rappresenta un avvolgimento occorre tener conto del tipo di conduttore: natura, lunghezza e sezione che essenzialmente ne definiscono la resistenza R . Inoltre l’avvolgimento stesso presenterà una induttanza L più o meno elevata a seconda che sia avvolto ad esempio su un supporto in legno, anziché su un nucleo in ferro. Semmai possono trascurarsi le capacità C fra spira e spira, ma nella rappresentazione utile al calcolo delle correnti e tensioni in gioco si distinguono, separatamente, resistenza e reattanza, cioè elementi concentrati, che si ritengono costanti. Sostanzialmente il concetto di impedenza rappresenta l’ostacolo che interessa lo studio del comportamento in regime sinusoidale e in tal caso ad essa contribuiscono la resistenza e la reattanza induttiva, nel modo che ora si descriverà. L’impedenza è un operatore complesso che esprime il legame tra la tensione presente ai suoi estremi e la corrente, che variano nel tempo (noi esaminiamo qui grandezze sinusoidali), mentre essa non è funzione del tempo. L’impedenza è l’ostacolo al passaggio della corrente e, a differenza del comportamento in corrente continua dove l’ostacolo è rappresentato dalla resistenza (l’induttanza si comporta come un corto circuito, la capacità come un circuito interrotto), in corrente alternata l’ostacolo tiene conto anche delle eventuali reattanza induttiva XL e reattanza capacitiva XC . Tutti questi ostacoli sono misurati in ohm [Ω] . L’impedenza viene calcolata dal rapporto fra la caduta di tensione ai suoi capi e la corrente che la percorre, se i componenti ideali sono in serie: e tutte e tre le grandezze sono qui interpretate come numeri complessi. Tenendo presenti le conclusioni riportate in fig.7 del paragrafo precedente, si considerano ora circuiti reali costituiti dalla serie R-­‐‑L e R-­‐‑C e da collegamenti misti serie-­‐‑parallelo. 11a)_Circuito ohmico-induttivo R-L con resistenza e reattanza in serie. Impedenza
In figura 1) vi è lo schema riferito ad un generatore di tensione sinusoidale, di valore efficace U, che alimenta la serie di una resistenza R e di una bobina di induttanza L, la cui reattanza induttiva vale XL = ω L = 2πf L [Ω] La corrente che attraversa gli ostacoli “resistenza e reattanza induttiva” è la stessa e dà luogo a due cadute di tensione: UR ai capi della resistenza R, in fase con la corrente (fig. 1b); UL ai capi della reattanza induttiva XL, in anticipo di 90° rispetto alla corrente stessa. La loro somma U, di tipo vettoriale è la c.d.t. totale ai capi dell’impedenza Z e coincide anche, naturalmente, con la tensione che deve fornire il generatore (fig.1). L’impedenza induttiva Z rappresenta l’ostacolo totale offerto dal circuito in esame al passaggio della corrente. 40 Figura Errore. Il segnalibro non è definito.) a) Schema del circuito serie ohmico induttivo; b)
diagramma vettoriale tensioni-corrente – triangolo delle cadute di tensione; c) triangolo
dell’impedenza. Si osservi che i lati del triangolo dell’impedenza non sono vettori, poiché, come si
ricorderà, si era assunto di associare alle grandezze sinusoidali i vettori (qui i lati del triangolo non
corrispondono a sinusoidi).
Il calcolo mediante i moduli, che va effettuato considerando la posizione dei vettori nel piano di Gauss, porta ai risultati seguenti (fig. 1b e 1c): Dai triangoli simili delle cadute di tensione (vettori) e dell’impedenza si può dedurre anche lo sfasamento di cui la tensione totale anticipa la corrente che percorre l’impedenza (è lo stesso dire che la corrente è in ritardo rispetto alla tensione ai capi dell’impedenza) L’angolo si può ricavare, ad esempio, da una delle seguenti relazioni trigonometriche: ESEMPIO
Un generatore alimenta, con tensione sinusoidale di frequenza f=50Hz, il circuito di fig.1 a) erogando una corrente di valore efficace I=4A. L’impedenza è costituita da una bobina di induttanza L=8,6mH e la resistenza complessiva dell’avvolgimento risulta essere R=2Ω. Ritenendo costante l’induttanza della bobina si calcolino le cadute di tensione e la tensione, in valore efficace, che deve fornire il generatore. _________ Si calcola la reattanza con l’espressione 41 XL = ω ·∙ L = 2πf ·∙ L = 314 ·∙ 8,6 ·∙ 10-­‐‑3 = 2,702 Ω La corrente dà luogo alla caduta UR in fase con essa e alla UX a 90° in anticipo. Per determinare la tensione totale U si segue il procedimento indicato, ottenendo: in cui l’impedenza, ostacolo complessivo del circuito, è Passando ai moduli: che rappresenta il valore efficace richiesto. Desiderando conoscere il modulo dell’impedenza si calcola Lo sfasamento di cui la tensione totale anticipa la corrente e quindi lo sfasamento caratteristico dell’impedenza si può determinare ad esempio così: In fig. 1b) è rappresentato il diagramma vettoriale, che si è tracciato ponendo sull’asse reale la corrente, nota dal testo. Rispetto alla corrente vengono rappresentate le cadute di tensione e di conseguenza la tensione totale U , in anticipo di 53,49°. La soluzione si può anche determinare graficamente, riportando in scala le tensioni. Per inciso si osserva che, dovendo rappresentare in scala anche le correnti, la scala scelta non è generalmente la stessa. La scelta va fatta in base allo spazio che si ha a disposizione e all’evidenza che si vuole assegnare alle grandezze. Osservazione
Nelle applicazioni numeriche, soprattutto per chi non ha ancora dimestichezza per questi procedimenti, si faccia bene attenzione a tener conto delle posizioni dei vettori. Di conseguenza si ricordi che, a differenza di quanto accade in corrente continua, le somme sono sempre vettoriali, sia che si sommino tensioni, sia che si sommino correnti, sia che si sommino impedenze in serie. 42 Infatti 4+3 non fa 7!!!! a meno che il vettore di modulo 4 e quello di modulo 3 sia allineati, con stessa direzione e stesso segno!!! Nell’esempio riportato sopra, la somma delle c.d.t. UR e UX non è numerica, ma vettoriale: i due vettori rappresentativi sono fra loro a 90° e quindi la somma si è potuta dedurre, in modulo, con il teorema di Pitagora. Circuito ohmico-capacitivo R-C con resistenza e capacità in serie. Impedenza
Figura Errore. Il segnalibro non è definito. a) Circuito R-C serie; b) diagramma tensioni-corrente e
triangolo delle cadute di tensione; c) triangolo dell’impedenza.
Rispetto al circuito R-­‐‑L, qui la presenza del condensatore di capacità C che ritarda la propria caduta di tensione di 90°, porta a spostare anche in ritardo la tensione totale rispetto alla corrente (dell’angolo φ, inteso negativo perché contato con verso orario a partire dalla posizione dell’asse reale positivo del piano di Gauss). Le considerazioni precedenti sono quindi influenzate dal segno meno della reattanza capacitiva –jXC , che si calcola, in modulo: Pertanto, con riferimento alla fig. 2, si scrivono le seguenti relazioni: in cui l’impedenza totale del circuito ohmico-­‐‑capacitivo è 43 I moduli e l’argomento si determinano così: ESEMPIO
Un generatore alimenta, con tensione sinusoidale di frequenza f=50Hz e valore efficace 230V, il circuito di fig.2 a). L’impedenza è costituita da una resistenza R=100Ω, mentre la capacità ad essa in serie è di 10µμF . Si calcolino la corrente nel circuito, le cadute di tensione e si rappresenti il diagramma vettoriale tensioni-­‐‑corrente. ______ Per la soluzione si calcola dapprima l’impedenza, per poi passare alla valutazione della corrente in modulo e fase e al tracciamento del diagramma. Si assume la tensione fornita dal testo sull’asse reale (fig.3b), per cui vettorialmente la tensione viene rappresentata con la sola parte reale. La corrente e le cadute di tensione saranno quindi riferite alla posizione del vettore tensione. Sostanzialmente il diagramma di fig. 2c) è come se fosse ruotato in senso antiorario dell’angolo caratteristico φ dell’impedenza: la corrente è comunque in anticipo rispetto alla tensione totale U fornita dal generatore (fig. 3b). Calcolo della reattanza capacitiva: 1) soluzione con metodo vettoriale: Ricordando che nel rapporto fra numeri complessi occorre moltiplicare numeratore e denominatore per il complesso coniugato del denominatore, si calcola la corrente con modulo 44 2) Soluzione con i moduli: 3) Soluzione con metodo esponenziale: • Si verifichi che la somma vettoriale delle c.d.t. parziali dà la tensione del generatore. • Il valore massimo di tensione che deve sopportare il condensatore e per il quale va dimensionato l’isolamento è 45 Figura: Triangolo dell’impedenza capacitiva; b) diagramma vettoriale avente come riferimento
sull’asse reale la tensione totale assegnata dal problema. Le tensioni e il triangolo dell’impedenza
rispettano le proporzioni in base alle rispettive scale (qui non indicate).
46 47