Sommario
Corso di Statistica
Facoltà di Economia
z
La diseguaglianza di Cebicev
z Variabili Casuali doppie
z Momenti di Variabili Casuali doppie
Lezione n° 17
a.a. 20002000-2001
Francesco Mola
a.a. 2000-2001
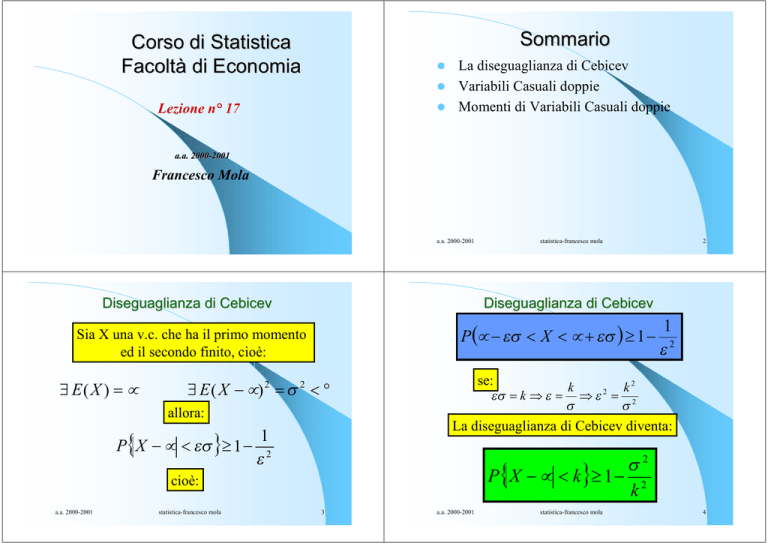
Diseguaglianza di Cebicev
P(µ − εσ < X < µ + εσ ) ≥ 1 −
k
k2
2
εσ = k ⇒ ε = ⇒ ε = 2
σ
σ
La diseguaglianza di Cebicev diventa:
1
P{X − µ < εσ }≥ 1 − 2
ε
σ2
P{X − µ < k }≥ 1 − 2
k
cioè:
statistica-francesco mola
1
ε2
se:
∃ E( X − µ )2 = σ 2 < ∞
allora:
a.a. 2000-2001
2
Diseguaglianza di Cebicev
Sia X una v.c. che ha il primo momento
ed il secondo finito, cioè:
∃ E( X ) = µ
statistica-francesco mola
3
a.a. 2000-2001
statistica-francesco mola
4
V.C. Doppie
v.c. doppie discrete
z Una
V.C. doppia (X,Y) associa ad ogni
evento dello spazio campionario una coppia
ordinata (x,y) di valori reali.
z Per tale variabile occorre definire la
probabilità del contemporaneo verificarsi di
un certo valore per la variabile X e di un
certo valore per la variabile Y.
P[(X = xi )∩ (Y = yi )] = pij
a.a. 2000-2001
statistica-francesco mola
Y
X
x1
x2
y1
p11
p21
xi
pi1
xk
pk 1
p•1
5
a.a. 2000-2001
h
j =1
statistica-francesco mola
p1•
p 2•
pi•
pk •
p
6
v.c. doppie continue
v.c. doppie discrete
pi• = ∑ pij
y 2 y j yh
p12 p1 j p1h
p22 p2 j p2 h
pi 2 pij pih
pk 2 pkj pkh
p•2 p• j p•h
X=continua e Y=continua
k
p• j = ∑ pij
Siano date:
i =1
(X , Y );
f ( X ); g (Y )
La probabilità congiunta è:
P[(x0 ≤ X ≤ x0 + dx ) ∩ ( y0 ≤ Y ≤ y0 + dy )] =
= ϕ (x0 , y0 )dxdy
Probabilità Marginali
a.a. 2000-2001
statistica-francesco mola
7
a.a. 2000-2001
statistica-francesco mola
8
v.c. doppie continue
v.c. doppie continue
Se è nota ϕ (x, y ) allora:
ϕ (x, y ) È una funzione di densità doppia
(o bivariata) tale che:
+∞
f ( x) = ∫ ϕ (x, y )dy
1) ϕ (x, y ) ≥ 0
−∞
+∞
+∞+∞
g ( y ) = ∫ ϕ (x, y )dx
∫ ∫ ϕ (x, y )dxdy = 1
2)
−∞
-∞ − ∞
a.a. 2000-2001
statistica-francesco mola
9
a.a. 2000-2001
Momenti misti di una v.c. doppia
statistica-francesco mola
Momenti misti scarto
Valore medio; valore atteso; Expectation
µ r ,s = E (X Y ) = ∑∑ x y pij
k
r
V.c. discrete
h
s
i =1 j =1
r
i
s
j
10
V.c. discrete
[
]
k
h
µ r , s = E ( X − µ x ) (Y − µ y ) = ∑∑ ( xi − µ x ) r ( y j − µ y ) s pij
r
s
i =1 j =1
V.c continue
µ r , s = E (X r Y s ) =
+∞ +∞
∫
r s
∫ x y ϕ (x, y )dxdy
V.c continue
− ∞− ∞
[
]
µ r , s = E ( X − µ x ) r (Y − µ y ) s =
=
+ ∞+ ∞
∫ ∫ (x − µ
x
) r ( y − µ y ) s ϕ (x , y )dxdy
− ∞− ∞
a.a. 2000-2001
statistica-francesco mola
11
a.a. 2000-2001
statistica-francesco mola
12
Momenti misti standardizzati
Casi particolari
V.c. discrete
µ r ,s
X − µ r Y − µ s k h X − µ r Y − µ s
y
y
x
x
= ∑∑
pij
= E
σ x σ y i =1 j =1 σ x σ y
V.c continue
µ r ,s
=
X − µ
x
= E
σ x
+ ∞+ ∞
X − µx
∫−∞−∫∞ σ x
a.a. 2000-2001
r
r
Y − µy
σ
y
Y − µy
σ
y
statistica-francesco mola
s
=
µ o ,o = 1
µ r ,o = E (X rY 0 ) = E (X r )
µ 0, s = E (X 0Y s ) = E (Y s )
s
ϕ (x , y )dxdy
13
a.a. 2000-2001
statistica-francesco mola
14
X e Y v.c. indipendenti
z Se X e Y sono indipendenti la conoscenza delle
Questo implica che:
v.c. componenti equivale statisticamente alla
conoscenza della v.c. doppia.
z Se e solo se X e Y sono indipendenti si ha,
rispettivamente per le discrete e le continue:
[
pij = pi p j
]
V.c. discrete
V.c continue
P (X = xi ) ∩ (Y = y j ) = P(X = xi )• P (Y = y j )
ϕ (x0 , y0 )dxdy = f ( x0 )dx • g ( y0 )dy
P[(x0 ≤ X ≤ x0 + dx ) ∩ ( y0 ≤ Y ≤ y0 + dy )] =
E quindi anche:
= P(x0 ≤ X ≤ x0 + dx )• P( y0 ≤ Y ≤ y0 + dy )
a.a. 2000-2001
statistica-francesco mola
15
µ r ,s = E (X r Y s ) = E (X r )E (Y s )
a.a. 2000-2001
statistica-francesco mola
16
X e Y v.c. NON indipendenti
X e Y v.c. NON indipendenti
z Se X e Y sono NON indipendenti si ricorre allo
z Al variare di Y si ha:
studio di v.c. condizionate.
p j|i = P (Y = y j | X = xi )
Y condizionata da X = x0 ⇒
P (Y = y | X = x0 ) =
P[(Y = y ) ∩ (X = x0 )]
P(X = x0 )
cioè p j|i =
ϕ(y|x0 ) =
a.a. 2000-2001
statistica-francesco mola
17
a.a. 2000-2001
µ r | x = E (Y | X = x ) = ∑ y p j|i = ∑ y rj
j =1
r
j
h
p ij
j =1
pi •
V.c continue
µ r|x
a.a. 2000-2001
statistica-francesco mola
ϕ(x0 , y)
f ( x0 )
V.c continue
statistica-francesco mola
18
COV (X , Y ) = σ xy è il momento misto di
Ordine (1+1) della V.C. Scarto
(X − µ )(Y − µ ) ⇒
+∞
r
pi•
covarianza è una misura esplicita del
legame esistente fra le componenti di una
v.c. doppia.
ϕ (y, x )
= E (Y | X = x ) = ∫ y ϕ ( y | x )dy = ∫ y
dy
f
x
(
)
−∞
−∞
+∞
r
V.c. discrete
z La
V.c. discrete
h
pij
Covarianza
Momenti condizionati
r
P[(Y = y ) ∩ (X = x0 )]
P( X = x0 )
x
r
19
a.a. 2000-2001
.
y
statistica-francesco mola
20
Covarianza (cont.)
Covarianza (cont.)
z Quando
scarti positivi (negativi) della v.c.
X si associano a scarti negativi (positivi)
della v.c.Y, abbiamo che:
V.c. discrete
k
h
⇒ ∑∑ ( xi − µ1, 0 ) r ( y j − µ 0,1 ) s pij
COV (X , Y ) < 0
i =1 j =1
z Quando
V.c continue
⇒
+∞ +∞
∫ ∫ (x − µ
1, 0
scarti positivi (negativi) della v.c.
X si associano a scarti positivi (negativi)
della v.c.Y, abbiamo che:
) r ( y − µ 0 ,1 ) s ϕ (x , y )dxdy
COV (X , Y ) > 0
− ∞− ∞
a.a. 2000-2001
statistica-francesco mola
21
a.a. 2000-2001
statistica-francesco mola
22
Covarianza (cont.)
graficamente
z Quindi
se in media X cresce (decresce) e in
media Y decresce (cresce), abbiamo che:
COV (X , Y ) < 0
COV (X , Y ) < 0
zQuindi
se in media X cresce (decresce) e in
media Y cresce (decresce), abbiamo che:
COV (X , Y ) > 0
COV (X , Y ) > 0
a.a. 2000-2001
statistica-francesco mola
La covarianza è quindi una misura sintetica
della relazione lineare tra X ed Y
23
a.a. 2000-2001
statistica-francesco mola
24
Calcolo di COV(X,Y)
= E [(XY − µ1,0Y − Xµ 0,1 + µ1, 0 µ 0,1 )] =
Calcolo di COV(X,Y)
= E (XY ) − µ1, 0 E (Y ) − E (X )µ 0,1 + µ1,0 µ 0,1 =
COV (X , Y ) = E ( X , Y ) − E ( X ) E (Y )
= E (XY ) − µ1, 0 µ 0,1 − µ 0,1µ1, 0 + µ1, 0 µ 0,1 =
Cioè la covarianza è uguale al momento
prodotto delle v.c. X e Y meno il prodotto
dei singoli momenti!
= E (XY ) − 2 µ1, 0 µ 0,1 + µ1, 0 µ 0,1 =
= µ1,1 − µ1, 0 µ 0,1 =
dim .
COV (X , Y ) = E [(X − µ1,0 )(Y − µ 0,1 )] =
a.a. 2000-2001
statistica-francesco mola
= E ( X , Y ) − E ( X ) E (Y )
25
26
(X − µ x ) (Y − µ y ) COV ( X , Y )
ρ xy = E
=
σ
σ
σ xσ y
x
y
z Una
misura della forza del legame lineare
tra le v.c. componenti (indipendente
dall’unità di misura delle stesse) è il
coefficiente di correlazione lineare.
Proprietà:
1) - 1 ≤ ρ xy ≤ 1
ρ xy
è il momento misto di
Ordine (1+1) della V.C. doppia standardizzata.
2) !xy = ±1
X − µ x Y − µ y
σ x σ y
statistica-francesco mola
statistica-francesco mola
Correlazione (cont.)
Correlazione
a.a. 2000-2001
a.a. 2000-2001
c.v.d.
iff
Y = α + βX
Perfetta relazione lineare tra X e Y
27
a.a. 2000-2001
statistica-francesco mola
28
X e Y indipendenti
X e Y indipendenti
E ( X , Y ) = E ( X ) E (Y ) ⇒
Quindi l’incorrelazione è condizione necessaria e
ma non sufficiente per l’indipendenza!
⇒ COV ( X , Y ) = E (X , Y ) − E ( X ) E (Y ) =
= E (X )E (Y ) − E ( X ) E (Y ) = 0
Quindi X e Y indipendenti implica che
COV(X,Y)=0, cioè X e Y sono anche incorrelate.
La covarianza non consente di pervenire ad una
forza del legame tra X e Y, perché essa dipende
dall’unità di misura delle v.c. componenti.
Attenzione!!!
COV(X,Y)=0, non implica che X e Y sono
indipendenti
a.a. 2000-2001
statistica-francesco mola
29
a.a. 2000-2001
statistica-francesco mola
30