Fisica Medica 2007/8
IMPEDENZA TISSUTALE
Vorrei comprendere meglio il concetto di impedenza tissutale elettrica da noi studiato in fisica
medica. In particolare vorrei capire perché un tessuto in risonanza abbia un impedenza in cui la
componente reattiva si annulla. Vi ringrazio.
Come noto un campione di materiale può essere caratterizzato dal punto di vista elettrico valutandone il
comportamento che assume quando ad esso è applicata, tramite elettrodi, una tensione elettrica. A seconda delle
proprietà conduttrici del materiale, l'entità del flusso di corrente elettrica provocata all'interno del campione dalla
tensione applicata assume valori molto diversi. Nel caso semplice di sollecitazione in tensione di valore costante
(regime continuo) il parametro che descrive l'entità della corrente è la resistenza elettrica (simbolo convenzionale
R).
Qualora la tensione elettrica non abbia valore costante ma variabile nel tempo con andamento periodico
sinusoidale, la corrente che si sviluppa risulta avere (salvo rari casi) anch'essa andamento sinusoidale con lo
stesso periodo o, equivalentemente, la stessa frequenza di oscillazione. In questo caso, tuttavia, la corrente
elettrica è caratterizzata da due grandezze anziché una:
- l'ampiezza, che descrive il valore massimo dell'oscillazione di corrente;
- la fase relativa, ovvero il ritardo temporale (o l'anticipo!) che l'onda sinusoidale di corrente assume rispetto
all'onda sinusoidale di tensione.
Queste informazioni sono riassunte dalla grandezza impedenza elettrica (simbolo convenzionale Z) che
rappresenta l'estensione formale della resistenza nel caso, peraltro molto frequente, di regime sinusoidale. È
fondamentale ricordare qui che l'impedenza è rappresentabile da un numero complesso la cui parte immaginaria
dipende dalla frequenza (f) dell'onda di tensione sollecitante.
Ovviamente anche una sostanza organica, quale una fibra o un tessuto, può essere caratterizzata dal punto di vista
elettrico; si parla, pertanto, di impedenza tissutale.
L'effetto di risonanza può essere illustrato facendo riferimento alla rappresentazione schematica di un campione
di materiale in Figura 1.
Figura 1 - Semplice esempio di circuito risonante sollecitato dalla tensione sinusoidale V. In evidenza
anche le cadute di potenziale sui singoli elementi.
La resistenza R coincide, per basse frequenze, al valore di resistenza in regime continuo, la capacità C riassume
gli effetti di accumulo di carica elettrica sul tessuto mentre l'induttanza L descrive gli effetti magnetici dovuti alla
corrente variabile. La rappresentazione di Figura 1 è puramente astratta, nel senso che non è banale associarvi
porzioni di tessuto né valutare il valore dei parametri necessari per analizzare a livello quantitativo il fenomeno.
Per la rete generale di Figura 1 l'impedenza complessiva vale:
dove il termine 2πfL prende il nome di reattanza induttiva (XL) e 1/(2πfC) si dice reattanza capacitiva (XC).
Osservando la (1) si nota che esiste un particolare valore della frequenza f per la quale la componente induttiva
bilancia la componente capacitiva annullando la parte immaginaria dell'impedenza. Dal punto di vista intuitivo si
può interpretare il fenomeno considerando che il ritardo dell'onda di corrente rispetto all'onda di tensione
provocato dagli effetti induttivi (L) sia perfettamente compensato dall'anticipo tra le onde stesse provocato dagli
effetti capacitivi (C). In effetti capacità e induttanze rappresentano fenomeni descritti dalle equazioni di Maxwell
dell'elettromagnetismo e rispecchiano la rispettiva dualità tra campo elettrico e magnetico.
In queste condizioni, di risonanza appunto (in particolare risonanza "serie"), l'impedenza è una grandezza
puramente reale e coincide con la resistenza R; ciò significa che la corrente elettrica ha sfasamento (cioè
differenza di fase ovvero ritardo) nullo rispetto alla tensione (le onde si dicono appunto "in fase"). Per la legge di
Ohm la corrente ha ampiezza massima:
indipendente dai valori di L e C.
Ancora dalla (1) risulta molto semplice valutare la frequenza alla quale si manifesta la risonanza. Infatti, affinché
si annulli la componente immaginaria dell'impedenza deve essere:
da cui:
Si osservi che tale frequenza dipende esclusivamente dalle componenti reattive L e C ma non dalla resistenza R
che interviene, d'altra parte, quale unico parametro per la definizione dell'ampiezza della corrente alla risonanza,
vedi (2).
Come curiosità si osservi che la tensione ai capi della resistenza ha ampiezza massima VR,MAX=IMAX*R=VMAX,
cioè pari all'ampiezza massima della tensione applicata ai capi dell'intera rete mentre le tensioni massime ai capi
della capacità C e dell'induttanza L sono rispettivamente:
Si osservi inoltre che per valori di induttanza elevati e capacità piccole le tensioni VC,MAX e VL,MAX possono
superare l'ampiezza massima della tensione applicata (VMAX); questo risultato, apparentemente sorprendente, è
dovuto ad uno scambio reciproco di energia tra condensatore ed induttanza che non coinvolge la sorgente esterna.
In condizioni di risonanza lo scambio è massimo perché l'energia elettrica immagazzinata nel condensatore C è in
opposizione di fase all'energia magnetica contenuta nell'induttore L: quando uno dei due acquista energia l'altro la
cede. Pertanto, le tensioni VC,MAX e VL,MAX, alla risonanza, hanno uguale ampiezza (basta sostituire la (3) nelle
espressioni appena trovate) ma verso, istante per istante, opposto: nella somma, vedi Figura 1, tutta la differenza
di potenziale V è sostenuta dalla resistenza.
In Figura 2 è riportata un esempio di impedenza al variare della frequenza: sono evidenziati modulo (Figura 2a) e
fase (Figura 2b) della grandezza completa Z. Si osservi che, come dimostrato, per f=fo (risonanza) l'impedenza è
minima in modulo (L e C non giocano più nessun ruolo) e il ritardo di fase è nullo.
Le applicazioni della risonanza sono svariate in tutti i campi dell'ingegneria e della fisica; in particolare, in ambito
medico, si rivela utile lo studio dell'impedenza tissutale allo scopo di evidenziare anomalie del tessuto organico,
indice di eventuali disfunzioni o patologie.
APPLICAZIONE
Indicazioni e limiti della Radiofrequenza in dermatologia
La Radiofrequenza (RF) rappresenta una recente ed interessante metodica nel
trattamento
di
alcuni
inestetismi
quali
l’adiposità
localizzata,
la
panniculopatia edemato-fibro-sclerotica (P.E.F.S.), meglio conosciuta con il
nome di “cellulite”, l’invecchiamento cutaneo e le teleangiectasie.
L’apparecchiatura consta di un generatore di corrente alternata ad alta
frequenza, di manipoli con caratteristiche diverse in funzione delle patologie da
trattare e forniti di un intrinseco sistema di raffreddamento essenziale per evitare
il surriscaldamento dell’epidermide. Il principio su cui si basa questa metodica
consiste nel riscaldamento controllato del tessuto, derma o sottocute, mediante
l’induzione di un campo elettromagnetico che determina nel tessuto interessato
una complessa e variegata risposta in funzione della modalità applicativa
prescelta. La RF permette di trasmettere, in maniera controllata, calore ai tessuti
sottostanti molto più in profondità di qualsiasi altro sistema ed in particolare della
metodica laser. Il manipolo bipolare presenta al suo interno due elettrodi (+/-)
che eccitati generano un campo elettromagnetico con una profondità di circa 3-6
mm. L’utilizzo bipolare è peculiare per il trattamento dell’invecchiamento del
viso, collo e decolleté. Può essere usato da solo o meglio abbinato a sorgente
laser anche per il trattamento delle teleangiectasie. Il manipolo monoplare è
costituito da un unico elettrodo che genera, sempre attraverso la costituzione di
un campo elettromagnetico, un riscaldamento controllato molto più profondo che
nella modalità bipolare, arrivando sino a 4-6 cm di profondità. L’intensità del
riscaldamento è in funzione della conducibilità tissutale ed in particolare modo
della resistenza che ogni specifico tessuto oppone a farsi attraversare da una
corrente elettrica. Questa resistenza, chiamata impedenza, varia notevolmente in
funzione delle peculiarità del tessuto da trattare. Ad esempio, il sangue offre
un’impedenza certamente maggiore al grasso, la cute disidratata si lascia più
facilmente attraversare rispetto ad una cute ben idratata. Questi concetti fisici
sono basilari per l’applicazione pratica di questa metodica, che deve essere
quindi personalizzata per ogni paziente e distretto. In modalità bipolare, come
innanzi accennato, la RF è particolarmente indicata nel trattamento dell’invecchiamento cutaneo sia cronologico sia fotoindotto. In particolare agisce sul
trofismo del tessuto cutaneo migliorandone anche il tono. Il campo
elettromagnetico indotto dal manipolo, con il conseguente rialzo termico del
derma, induce una intensa stimolazione dei fibroblasti cui consegue la liberazione
di sostanze vasoattive che riattivano il microcircolo ed una contestuale
fibrillopoiesi e collagenogenesi che giustifica l’effettivo miglioramento
dell’obiettività clinica. In eguale misura si osserva un ricompattamento del
collageno preesistente che si dispone in maniera più ordinata sui piani spaziali.
Non c’è necessità di anestesia ed il paziente, terminata la seduta, può
tranquillamente riprendere la sua quotidianità e può truccarsi, se lo vuole. In
modalità unipolare la RF è particolarmente indicata nel trattamento della
adiposità localizzata e di quella condizione clinica identificata con l’acronimo di
P.E.F.S., meglio conosciuta dall’utenza con il termine di “cellulite”. E’ bene
precisare con i risultati migliori si hanno nel trattamento dell’adiposità localizzata
in virtù dell’assenza delle anomalie anatomico-strutturali presenti nella P.E.F.S.
responsabili di una maggiore resistenza del tessuto a farsi attraversare
dall’impulso elettrico. La modalità utilizzata in entrambi i casi è quella
monopolare. In questo caso, il campo elettromagnetico indotto dal manipolo,
determina un riscaldamento termico del tessuto in profondità(4-6 cm) con
duplice azione: 1- intensa attivazione del microcircolo con associato migliorato
drenaggio (qualora trattasi di cellulite), 2- alterazione della carica elettrica
citoplasmatica adipocitaria con conseguente attività lipolitica. La metodica non è
invasiva ed è praticamente indolore, considerato che il paziente percepisce
soltanto una sensazione di calore più o meno intensa secondo l'individuale
sensibilità ed i parametri operativi utilizzati. E’ bene ricordare che i
miglioramenti, già riscontrabili dopo le prime sedute, si stabilizzano ulteriormente
nel prosieguo e sono decisamente più eclatanti se si abbina un’adeguata attività
motoria ed igiene alimentare. Particolarmente interessante è l’utilizzo della RF nel
trattamento delle teleangiectasie. In questo caso spesso viene associata con
sorgenti laser il cui spot viene preceduto da un’emissione di RF che ne potenzia
l’effetto, preriscaldando il “target”. I campi di utilizzo innanzi descritti meritano
comunque un’attenta valutazione anche istologica, carenza questa frequente in
campo dermoestetico. L’autore pertanto propone un’ampia carrellata di quadri
clinici che attestano l’efficacia di questa nuova offerta terapeutica pur
evidenziandone i limiti e le precise modalità d’uso
DESCRIZIONE DELL'UTILIZZO
1 Porre il soggetto in posizione
orizzontale, con le gambe e le braccia
leggermente divaricate per 5 minuti,
onde
permettere
un'omogenea
distribuzione dei fluidi corporei.
Non è richiesta alcuna preparazione del soggetto
2 Applicare i 4 elettrodi adesivi.
Applicare le 4 pinzette ai relativi
elettrodi (2 pinzette nere e 2 pinzette
rosse) come mostrato in figura.
3 Accendere lo strumento e leggere i
valori di Massa cellulare, Acqua
extracellulare, Metabolismo basale e Angolo
di fase espresso in gradi (indice della qualità
cellulare)
MODALITA' STA
che compaiono sul display.
PER USARE STA NELLA MODALITA' BIA SI
EFFETTUANO COMUNQUE LE AZIONI DESCRITTE
AI PUNTI 1 E 2 SALVO POI LEGGERE SUL DISPLAY I
VALORI DI RESISTENZA E REATTANZA.
4 Inserire i valori di Resistenza e
Reattanza mostrati dallo strumento
nel software in dotazione. Per ogni
soggetto viene creata una scheda
nella quale trovano posto i dati
antropometrici e le varie analisi
effettuate
che
consentono
di
monitorare le condizioni del soggetto
nel tempo.
5 Il software elabora i dati fornendo un
rapporto dettagliato del soggetto in
termini quantitativi. Esso mostra tutti
i parametri misurati dal BIA-101
nell’unità di misura (kg, Lt o Kcal) e
in percentuale. In questo caso siamo
di fronte ad un soggetto che ha una
massa grassa del 17,3% ed una massa
muscolare di 57,4 kg su un peso
complessivo di 88 kg. L’angolo di
fase di 9,1 denota un’elevata vitalità.
Il metabolismo basale viene misurato
in 2404 Kcal.
6 Consultare i valori di riferimento
presenti a video per identificare
l’eventuale scostamento dalla norma
dei parametri misurati.
7 Attivare il grafico Biavector. Questo strumento grafico, Clinicamente validato, permette di
individuare lo stato del soggetto riuscendo a discriminare tra buona e cattiva nutrizione, l’obeso
dall’atleta, il magro dal cachettico o dall’anoressica, misurare l’idratazione e segnalare l’eventuale
catabolismo muscolare.
In questo caso viene esaminato un soggetto che non riusciva ad incrementare la propria massa
muscolare a causa di uno stato catabolico causato da cattiva alimentazione ed eccessivo
allenamento.
Prima misurazione
Seconda misurazione (3 mesi dopo)
Catabolismo muscolare causato da
stress e cattiva alimentazione
Migliorato l’apporto nutrizionale e
ottimizzato l’allenamento
BiaVector® Clinicamente validato
Aumento ponderale di kg 0,5
La massa cellulare è aumentata di kg. 2,3
La Massa grassa è diminuita di kg 1,8.
Aumentato il metabolismo basale in seguito all’aumento
di massa cellulare.
8 Stampare il rapporto d’analisi che
riporta il nome dello Studio e del
Centro Sportivo assieme ai dati del
soggetto e agli eventuali grafici
selezionati.
9 Grazie ai valori misurati dai nostri Bioanalizzatori è subito possibile decidere gli opportuni
interventi dietetici, farmacologici o motori che potranno essere monitorati nel tempo.
Tutorial di matematica
Potenze, radici, logaritmi
01 - Potenze.
Con i numeri reali si possono fare le quattro usuali operazioni + - · / .
Con i numeri reali si possono fare anche le potenze che, però, con costituiscono una nuova
operazione.
Si tratta in effetti di una sequenza di moltiplicazioni.
La potenze sono molto utili perché con esse è possibile mettere in forma abbreviata e compatta
numeri
anche molto grandi e perché soddisfano importanti ed utili proprietà.
Per esempio, la distanza terra-sole è di 150.000.000 km . Questo numero può essere scritto come:
km
oppure, come si usa nella notazione scientifica (la stessa delle calcolatrici elettroniche) :
km .
Ancora, la terra dista da Alpha Centauri 40.000.000.000.000 km . Usando le potenze si ha :
km .
Il vantaggio di usare le potenze (specialmente quelle a base 10 ) è innegabile !
Una potenza, quindi è un "oggetto" matematico in cui un numero funge da base ed un altro da
esponente :
La definizione di potenza è la seguente :
la potenza è il prodotto di fattori uguali alla base tante volte quanto indicato dall'esponente.
Per esempio :
.
Si noti che
per cui l'operazione di elevamento a potenza non è commutativa rispetto allo
scambio
fra base ed esponente.
La potenza ammette due tipi diversi di operazione inversa : la radice ed il logaritmo.
Usando le lettere invece dei numeri, cosa molto comoda in matematica perché ci permette di
ottenere
formule generali valide per tutti i numeri, la definizione di potenza vale :
dove la moltiplicazione è effettuata n volte.
Si noti che n deve essere un numero intero maggiore di 1 . Questa precisazione è necessaria
perché
per avere un prodotto occorrono almeno due fattori. Vedremo più avanti come sia possibile
definire
potenze con esponente 1 , 0 o addirittura negativo e frazionario.
Se la base è 10 , si ha la semplice regola che il numero che si ottiene è formato da 1 seguito da un
numero
di 0 pari all'esponente. Esempi :
.
02 - Proprietà delle potenze.
Le potenze soddisfano le seguenti fondamentali proprietà :
- 1 - il prodotto di due potenze di ugual base è uguale ad una potenza che ha per base la
stessa
base e per esponente la somma degli esponenti :
.
Esempio :
.
- 2 - il quoziente di due potenze di ugual base è uguale ad una potenza che ha per base la
stessa
base e per esponente la differenza degli esponenti :
.
Esempio :
.
- 3 - la potenza di una potenza è uguale ad una potenza di ugual base elevata ad un
esponente
uguale al prodotto degli esponenti :
.
Esempio :
.
03 - Esponenti ... particolari.
Nella definizione di potenza abbiamo posto la condizione che l'esponente debba essere maggiore
di 1,
quindi possa prendere i valori 2, 3, 4 ...
Cosa succede se immaginiamo di elevare una base ad un esponente uguale a 1 , a 0 o addirittura
ad
un numero negativo (per gli esponenti frazionari vedi più avanti) ?
Secondo la definizione di potenza data in precedenza, queste operazioni sarebbero impossibili. E'
però
possibile una loro definizione estendendo il concetto di potenza, considerandola in senso più
generalizzato.
Queste operazioni sono allora possibili (sotto certe condizioni) e la loro definizione è tale da
"salvare" le
proprietà delle potenze. Useremo allora le proprietà delle potenze per definire questi nuove
operazioni.
Vediamo in dettaglio :
- 1 - esponente uguale a 1 :
Consideriamo la divisione 10 ³ / 10 ² = 1000 / 100 = 10 .
Utilizzando le proprietà delle potenze il risultato sarebbe
Non abbiamo ancora definito
Se definiamo
.
.
, la seconda proprietà delle potenze rimane valida.
Generalizzando questo risultato a tutti i numeri, possiamo scrivere :
.
- 2 - esponente uguale a 0 :
Consideriamo la divisione 10 ² / 10 ² = 100 / 100 = 1 .
Utilizzando le proprietà delle potenze il risultato sarebbe
Non abbiamo ancora definito
Se definiamo
.
.
, la seconda proprietà delle potenze rimane valida.
Generalizzando questo risultato a tutti i numeri, possiamo scrivere :
.
Si noti che si deve porre la condizione
perché non si può dividere per zero.
- 3 - esponente negativo :
Consideriamo la divisione
.
Utilizzando le proprietà delle potenze il risultato sarebbe
Non abbiamo ancora definito
Se definiamo
.
.
, la seconda proprietà delle potenze rimane valida.
Generalizzando questo risultato a tutti i numeri, possiamo scrivere :
.
Si noti che si deve porre la condizione
perché non si può dividere per zero.
04 - Potenze a base 2 .
Oltre alle potenze a base 10 , rivestono un ruolo molto importante quelle a base 2 .
L'aritmetica con cui "funzionano" i computers è a base 2 !! Le informazioni (numeri, parole ecc .)
che
vengono elaborate o memorizzate in un computer sono codificate come sequenze di bit. Un bit
(binary
digit) è la più piccola unità di informazione e può prendere i valori : 0 oppure 1 .
Un byte è una sequenza di 2 ³ = 8 bit . Per esempio :
00110101
è il possibile contenuto di un byte.
Il Kb (chilobyte) corrisponde a
bytes, cioè 1024 bytes (non 1000 come erroneamente molti
pensano !).
Il Mb (megabyte) corrisponde a
Il Gb (gigabyte) corrisponde a
Kb .
Mb .
Lasciamo al lettore il semplice calcolo di quanti bit è formato il Kb , il Mb ed il Gb .
05 - Radici.
Consideriamo la potenza 5 ³ = 125 . Possiamo allora definire l' "operazione" di radice a indice 3 (o
radice
terza) :
(dove il numero in alto a sinistra è l' indice mentre il numero sotto radice si chiama radicando), che
ha
come risultato quel numero che elevato all'indice dà il radicando. Infatti 5 elevato alla 3 dà 125 .
In questo caso, siccome l'indice è 3 , la radice si chiama anche radice cubica.
Se l'indice è 2 , la radice si chiama comunemente radice quadrata e, nello scriverla, si omette
l'indice :
.
La radice ad indice 1 è ovviamente il numero stesso, per cui :
perché 5 ¹ dà 5 .
La definizione di radice è allora :
Una radice secondo un certo indice di un numero dato è quel numero che elevato
all'indice
dà il numero dato.
Le radici degli esempi precedenti hanno come risultato numeri naturali. Questo non è però il caso
generale.
In generale una radice fornisce come risultato un numero irrazionale (numeri con infiniti
decimali non
periodici).
Esempi :
La radice è l'operazione inversa della potenza perché si ha sempre :
dove A è qualunque numero su cui si può estrarre la radice ed n è qualunque indice ( 1 , 2 , 3 , ...
).
06 - Logaritmi.
Esiste un altro modo di definire l'operazione inversa dell'elevamento a potenza : il logaritmo.
Consideriamo ancora la potenza 5 ³ = 125 . Chiediamoci : qual'è il numero per cui elevare la base
5 per ottenere 125 ? Ovviamente questo numero è 3 .
Abbiamo così definito il concetto di logaritmo. Scriviamo allora :
dove il numero 5 scritto in basso a destra del simbolo log si chiama base ed il numero di cui si
fa il logaritmo si chiama argomento.
La definizione di logaritmo è allora :
Il logaritmo di un numero secondo una certa base è quel numero per cui si deve elevare
quella base per ottenere il numero dato.
Esempi :
perché 10 ¹ = 10
perché 10 ² = 100
perché 10 ³ = 1000 .
Il calcolo del logaritmo non conduce sempre ad un risultato "semplice", come negli esempi dati. Per
esempio :
dove il risultato, essendo 11 compreso fra 10 e 100 , è compreso fra 1 e 2 ed è un numero
irrazionale.
Si può fare , ovviamente, il logaritmo di un numero reale qualunque (sotto certe condizioni che
vedremo
in seguito). Per esempio :
.
E' molto importante notare che :
perché 10 ° = 1
perché 5 ° = 1 .
Quindi, il logaritmo di 1 è sempre 0 , qualunque base (permessa) si scelga.
Si noti anche che :
perché
Si noti infine l'importantissimo caso :
.
.
Non esiste nessun numero per cui elevare la base 10 in modo che il risultato sia 0 !!!
Siamo arrivati all'importantissimo risultato che il logaritmo di 0 (fatto rispetto ad ogni base) non
esiste.
I logaritmi si possono fare rispetto a basi qualsiasi (sotto particolari condizioni). Quelli più usati
sono i
logaritmi a base 10 , i cosiddetti logaritmi decimali. Molto usati sono anche i logaritmi a base 2 .
Vi sono poi i logaritmi naturali o neperiani in cui la base è il numero e = 2,718 ... , il cosiddetto
numero di Nepero (John Napier, inglese, 1550 - 1617), che è un numero irrazionale di enorme
importanza in matematica.
Ritorneremo su questo numero e sulle sue proprietà in seguito.
I logaritmi naturali si indicano usualmente con la semplice sigla ln . Per esempio :
07 - Cenni sulla storia del logaritmo.
Il concetto di logaritmo risale a Nepero (John Napier, teologo scozzese 1550-1617).
Il matematico inglese Henry Briggs (1556-1630) perfezionò l' idea di Nepero e pubblicò nel 1617
(anno
della morte di Nepero) un libro contenente i logaritmi in base 10 dei numeri da 1 a 1000 .
I logaritmi in base 10 sono detti logaritmi decimali o volgari e venivano usati per "velocizzare" i
calcoli
prima dell'avvento delle calcolatrici e dei computer.
Il grande matematico svizzero Eulero (Leonhard Euler, 1701-1783) introdusse successivamente il
numero
irrazionale e = 2,718 ... che chiamò numero di Nepero in onore dell'inventore dei logaritmi.
Egli pose questo numero come base dei logaritmi che per questo vengono chiamati logaritmi
neperiani o
naturali.
Il perché fu introdotto un tale numero così "complicato" a fungere da base per i logaritmi, è da
ricercarsi
nelle particolari ed importanti proprietà analitiche che la funzione logaritmo naturale ha (le
vedremo in
seguito quando studieremo le derivate).
08 - Numero di Nepero.
Il numero di Nepero e può essere definito nei seguenti modi :
- 1 - Come limite della successione :
ovvero il limite della successione :
;
;
; ecc. ecc.
per n tendente all'infinito.
- 2 - Come limite della sommatoria (serie) :
ovvero :
.
In futuro approfondiremo i concetti di limite, successione e serie.
09 - Potenze a esponente frazionario.
Le radici possono essere espresse in forma di potenze ad esponente frazionario. Per esempio :
.
Il perché di questo risulta molto semplice se si considera che la radice è l'operazione inversa della
potenza e se si estende la proprietà della potenza di potenza agli esponenti frazionari :
.
Analogamente si ha :
,
,
.
In generale si ha :
.
dove a indica un numero.
Fine.
Funzioni elementari
Vedere il Link
FUNZIONI ELEMENTARI
Funzioni elementari. Introduzione ...
matmedia.ing.unina.it/Didattica/Proposte%20e%20questioni%20didattiche/Funzioni%20elementari/indice/indice.htm
- 6k - Copia cache - Pagine simili
Introduzione
Dispense di Matematica
Insiemi e Funzioni; Vettori; Funzioni inverse; Funzioni
esponenziali e logaritmiche; Limiti e casi di
indeterminazione; Sintesi sulle distribuzioni discrete ...
www.mclink.it/personal/MC2113/dispenseMatematica.html 16k - Pagine simili
Funzione Esponenziale
La funzione esponenziale è una delle più importanti funzioni in matematica.
La sua proprietà fondamentale è che la derivata della funzione esponenziale f(x) = ex è sé stessa.
A volte, specialmente nelle scienze, si indicano come funzioni esponenziali tutte quelle della forma
kax, dove a, chiamato base, è un numero reale positivo. Questo articolo si concentrerà inizialmente
sulla funzione esponenziale di base e.
Definizione grafica
Per i non esperti del formalismo matematico si può dire che un andamento esponenziale di tipo
crescente o decrescente si può costruire numericamente su un diagramma cartesiano fissando un
valore qualunque (positivo per semplicità) ed aggiungendo o togliendo sempre la stessa percentuale
dell'ultimo risultato ottenuto partendo dal valore prefissato avendo quantizzando l'asse X a passi
uguali per ognuna di queste operazioni. Viene solitamente indicata come
rappresenta la base del logaritmo naturale.
oppure
, dove
Come funzione della variabile reale x, ex è sempre positivo (sopra l'asse x) e crescente. Non tocca
mai l'asse x, sebbene giunga arbitrariamente vicino ad esso (in altri termini l'asse x è un asintoto
orizzontale al grafico). La sua funzione inversa, il logaritmo naturale, ln(x), è definita per tutti gli x
positivi.
Proprietà
Le funzioni esponenziali godono delle seguenti proprietà:
Esse sono valide per tutti i numeri reali a e b e tutti i numeri reali x ed y. Le espressioni contenenti
frazioni e radici possono spesso essere semplificate utilizzando la notazione esponenziale perché:
e, per ogni a e b numeri reali con a > 0, e per ogni intero n > 1:
Importanza della funzione esponenziale (derivata) [modifica]
L'uguaglianza tra la funzione esponenziale e la sua derivata,
(proprietà unica tra le funzioni reali di variabile reale) fa sì che la la funzione f(x) = ex e le funzioni
da essa composte risolvano tutta una classe di equazioni differenziali che esprimono in termini
matematici i più importanti problemi fisici. In particolare questo accade quando il tasso di crescita
(o di diminuzione) di una grandezza è proporzionale alla sua dimensione — come nel caso della
crescita illimitata della popolazione (vedi catastrofe malthusiana), di interesse composto
continuamente, o di decadimento radioattivo — allora si può scrivere la variabile come prodotto di
una costante per la funzione esponenziale del tempo.
In effetti molte equazioni differenziali danno origine a funzioni esponenziali, comprese l'equazione
di Schrödinger e l'equazione di Laplace, come pure le equazioni per il moto armonico semplice.
Esempio fisico di funzione esponziale [modifica]
Un esempio semplice è quello di un oggetto lanciato ad una velocità v0 in un mezzo viscoso. Se
supponiamo che la resistenza posta dal mezzo all'avanzamento dell'oggetto sia proporzionale alla
velocità v di quest'ultimo:
F = - kv
si ha una relazione tra la velocità e la sua variazione nel tempo (l'accelerazione a):
ma = -k v ovvero m dv/dt = -k v
E' possibile dimostrare che la soluzione di questa equazione è:
v = v0 e-t/tau = v0 e-t/(m/k)
Nel caso di un proiettile sparato nell'aria sarebbe più corretto supporre che la resistenza sia
proporzionale al quadrato della velocità, cionondimeno l'andamento della velocità nel tempo è
descritto da una funzione formata a partire dalla costante matematica e.
Formulazioni equivalenti
Formulazioni equivalenti di questa proprietà sono:
La pendenza del grafico in ogni punto è uguale all'altezza del grafico in quel punto.
Il tasso di crescita della funzione in x è uguale al valore della funzione in quel punto.
La funzione risolve l'equazione differenziale y′ = y.
Per quanto riguarda le funzioni esponenziali di altre basi:
Dunque qualunque funzione esponenziale è pari ad un multiplo costante della sua derivata.
Per lo studio delle funzioni di ogni
tipo,periodiche,armoniche,sawtooth,Fourier,si invita a
collegarsi al sito che segue.
Vi si trovano anche riferimenti ad argomenti di fisica
affrontati a lezione.
Lista di funzioni - Wikipedia
2.1 Funzioni polinomiali; 2.2 Funzioni periodiche
elementari; 2.3 Funzioni trascendenti elementari. 3
Funzioni speciali. 3.1 Antiderivate di funzioni ...
it.wikipedia.org/wiki/Lista_di_funzioni - 44k - Pagine
simili
Funzioni periodiche
Una funzione f(.) definita su tutto l'asse reale, si dice T-periodica , dove T è un numero positivo se
per ogni x risulta
f(x)=f(x+T). (1)
Osserviamo che una funzione T-periodica è anche nT-periodica per ogni intero positivo n. Si
chiama periodo della funzione periodica il più piccolo numero positivo tale che valga la (1).
Esempi di funzioni periodiche sono le funzioni sen(.), cos(.) e tg(.): le prime due di periodo , la
terza di periodo .
La somma di due funzioni periodiche non è necessariamente periodica!
Esempio La somma di due funzioni periodiche tali che il rapporto fra i loro periodi sia razionale è
una funzione periodica.
Esempio Lo stesso dicasi del prodotto.
In generale, le vibrazioni (onde) indipendentemente dalla loro origine (sonora, luminosa,meccanica)
sono la sovrapposizione di onde "semplici", chiamate onde sinusoidali pure. Queste sono del tipo:
Asen(x+). Introduciamo della terminologia:
1.
2.
3.
4.
5.
A è l'ampiezza;
è la pulsazione;
2 è il periodo;
il reciproco del periodo è la frequenza;
è lo sfasamento.
Vediamo il grafico di una funzione di questo tipo:
Addizione di onde Quando due onde si propagano nello stesso mezzo simultaneamente, esse
possono sommarsi. La somma di due onde "semplici" dello stesso periodo T è una onda sinusoidale
pura di periodo T :
consideriamo la funzione f(x)=Acos(x)+Bsen(x). Osserviamo che
f(x)=(A2+B2)1/2(A/(A2+B2)1/2 cos(x)+B/(A2+B2)1/2 sen(x)),
che i numeri s=A/(A2+B2)1/2 e c=B/(A2+B2)1/2 soddisfano la relazione c2+s2=1 e che quindi esiste un
angolo tale che c=cos e s=sen . Fissato , risulta allora
f(x)=(A2+B2)1/2(sen cos(x)+cos sen(x)) .
Applicando la formula di addizione per il seno, otteniamo che:
f(x)=(A2+B2)1/2sen(x+).
Moltiplicazione di onde Quando due onde di frequenze diverse si propagano nello stesso mezzo
esse possono moltiplicarsi. Ciò avviene, per esempio, nella cassa armonica di uno strumento o nel
nostro orecchio. In questo caso si dice anche che il mezzo è nonlineare. Consideriamo ad esempio la
funzione
g(x)=sen(2fx)sen(2Fx),
prodotto di una funzione di frequenza f e di una di frequenza F. In generale, per quanto già visto, g
non è una funzione periodica.
Ricordiamo la formula trigonometrica:
cos(a)-cos(b)=2 sen((a+b)/2) sen((a-b)/2).
Ponendo (a+b)/2=2f e (a-b)/2=2F e risolvendo rispetto ad a e b ricaviamo che a=2(f-F) e
b=2(f+F). Quindi usando la formula ricordata sopra, ricaviamo che la funzione g si può sc
rive come somma di una funzione di frequenza pari alla differenza e di una di frequenza pari alla
somma delle frequenze delle onde originali. In applicazioni musicali, risulta più intensa l'onda di
frequenza pari alla differenza, che prende il nome di terzo suono. La scoperta di questo fenomeno è
dovuta a G. Tartini nel 1714.
Fenomeni Transitori
Introduzione
In una rete elettrica con elementi reattivi, l'applicazione o la soppressione di
un'alimentazione, genera un fenomeno transitorio. Questo fenomeno si manifesta a causa
dell'inerzia presentata dagli elementi reattivi, che impediscono alle correnti e alle tensioni di
raggiungere il valore di regime istantaneamente. Ciò significa che il valore di regime viene
raggiunto gradatamente dopo un certo tempo, caratteristico della rete elettrica in esame. E'
noto, infatti, che:
a) un condensatore sottoposto ad una variazione di tensione non raggiunge istantaneamente
il valore finale;
b) un induttore, sottoposto ad una variazione della corrente non consente a questa di
raggiunge il valore finale istantanenamente.
Legge di Ohm per reti elementari
Lo studio dei fenomeni transitori riguarderà soltanto le reti elettriche lineari, per le quali
vale il principio della sovrapposizione degli effetti. Le reti elettriche, sottoposte a f.e.m
variabili, sono descritte dalla legge di Ohm per valori istantanei. In particolare per il circuito RL
serie:
L'equazione del circuito è un'equazione differenziale del I° ordine e lineare, perchè contiene
una derivata del primo ordine.
Per il circuito RC serie sottoposto ad una f.e.m. variabile nel tempo la legge di Ohm per i valori
istantanei presenta un intengrale. La tensione ai capi di un condensatore in funzione del
tempo, infatti, è data:
Dove il termine con l'integrale rappresenta la tensione ai capi del condensatrore C. E'
necessario effettuare qualche operazione su questo termine per trasformare la legge di Ohm
dalla forma integro-differenziale precedente alla forma di equazione differenziale del primo
ordine. Nell'equazione integro-differenziale, la tensione ai capi del condensatore è espressa dal
termine:
La risoluzione dell'equazione differenziale consente di determinare la tensione ai capi di un
generico condensatore.
Metodo di risoluzione dell'equazione differenziale di un circuito sottoposto a
transitorio
In un qualsiasi circuito elettrico sottoposto a brusche variazioni di tensione o di corrente,
nascono in queste delle componenti dette transitorie, le quali dopo un certo tempo si
estinguono ( da ciò il termine transitorio ). Le componenti transitorie, permettono alle
compenti permanenti, a cui i circuito tende necessariamente, di instaurarsi in modo graduale e
non in modo violento. Questo comportamento è dovuto alla presenza di induttanze e
condensatori che presentano una certa inerzia a lasciarsi coinvolgere in brusche variazioni di
corrente e tensione. Si può affermare che la tensione e la corrente di un circuito lineare, in
queste condizioni di transitorio, sono sempre date dalla somma di due termini:
a) un termine permanente, detto anche termine forzato, che si determina con i
calcoli relativi a circuiti in regime permanente;
b) un termine trasitorio, detto anche termine libero;
La risoluzione di qualsiasi problema inerente i transitori, richiede di determinare i valori delle
grandezze descritti ai punti a) e b) e, applicando la sovrapposizione degli effetti, risalire al
grandezza in funzione del tempo.
dove :
ip = termine permanente della corrente o corrente a regime;
itr(t) = termine transitorio della corrente.
vp = termine permanente della corrente o corrente a regime;
vtr(t) = termine transitorio della corrente.
Trovare i termini permanente e transitorio consente di conoscere l'espressione della
tensione e della corrente in un circuito sottoposto a transitorio. A questo scopo occorre
risolvere l'equazione differenziale che descrive il circuito applicanto i metodi dell'analisi
matematica. Esiste, in alternativa un metodo, che consente di pervenire alle stesse
conclusioni, utilizzando una parte di analisi matematica ed una parte di elettrotecnica: ad
esempio se si vuole conoscere la corrente che circola in un circuito RL serie sottoposto a
trasnitorio, per quel circuito vale la legge vista:
i(t) = ip + itr(t);
Dall'Elettrotecnica si determina il termine ip, cioè la corrente che rcircolerà nel circuito RL
quando il transitorio si è esaurito; l'analisi matematica fornisce l'espressione del termine
transitorio, che per un sistema del I° ordine qualsiasi è sempre del tipo:
itr(t) = A est
3)
dove:
A è una costante che si determina con le condizioni iniziali imposte al circuito;
s è una costante che si determina, di solito in due modi, e dipente dalle caratteristiche del
circuito. s è sempre uguale all'inverso della costante di tempo del circuito cambiata di segno.
La funzione esponenziale est
La funzione esponenziale est a seconda del valore dell'esponente s assume, nel tempo, i
seguenti andamenti:
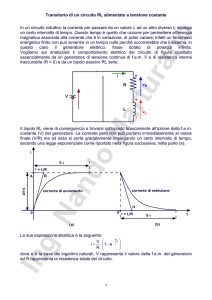
Il transitorio nel circuito RL serie
Dato il circuito di figura:
determinare l'andamento della corrente quando all'istante t = 0 viene portato l'interruttore T
dalla posizione 0 alla posizione. Dopo un tempo sufficientemente lungo, l'interruttore viene
portato nella posizione 2), determinare l'andamento della corrente che circola sull'induttanza.
Soluzione
La f.e.m. costante è fornita da un generatore ideale di tensione, che viene inserita
bruscamente quando il tasto passa dalla posizione 0 alla posizione 1. poi viene bruscamente
disinserita quando il tasto T viene portato nella posizione 2. Prima di procedere al calcolo vero
e proprio è necessario fissare una scaletta di lavoro per risolvere il problema del trasnitorio cui
è sottoposto il circuito RL di figura.
Fasi della soluzione
La risoluzione classica del transitorio a cui è sottoposto un circuito elettrico, prevede
alcune fasi:
a) scrivere la legge di Ohm per il circuito dato ( RL serie nel caso in esame ). L'equazione
che si ottiene è di tipo differenziale del primo ordine completa, perché contiene il termine
relativo all'alimentazione, fornita dal generatore ( vedi equazione 1) );
b) la grandezza elettrica, di cui si vuole determinare l'andamento in funzione del tempo,
viene espressa come somma di due termini: il termine permanente ed il termine transitorio.
Nel circuito RL serie la grandezza elettrica è la corrente, perché l'equazione 1) esprime il
legame tra la variabile indipendente, il tempo, e la variabile dipendente, la corrente. Quindi:
i(t) = ip + itr(t);
c) si calcola il termine permanente, in assenza di transitorio, con le regole viste in
Elettrotecnica;
d) si calcola il termine transitorio, espresso da una sola funzione esoponenziale, perché
l'equazione differenziale del circuito è del primo ordine, come indicato dall'equazione 3). La
funzione esponenziale suddetta contiene due costanti A ed s che vanno calcolate caso per caso
perché dipendono dal circuito in esame e dalle condizioni in cui si trova il circuito stesso. La
costante A, detta ampiezza della funzione esponenziale, viene calcolata con le condizioni
iniziali, imponendo t= 0 per la grandezza eletterica sottoposta a transitorio. La costante s è
legata alla costante di tempo del circuito.
Calcoli
Il punto a) si attua partendo dal circuito elettrico.
Il punto b) definisce il legame tra la grandezza sottoposta a transitorio e il tempo:
i(t) = ip + itr(t)
Sostituendo al termine transitorio la 3) si ottiene:
i(t) = ip + A est
4)
Il punto c) Calcolo del termine permanente. Il termine permanente nela caso dell'esempio
in oggetto è la corrente che circola nel circuito quando il transitorio si è esaurito e
precisamente:
Il punto d) Calcolo del termine transitorio, prevede due parti: il calcolo di A ed il calcolo di
s.
A,ì si determina con le condizioni iniziali. Inizialmente, con l'interruttore nella posizione 0, la
corrente del circuito vale 0, e vale altrettanto nell'istante in cui l'interruttore T viene portato,
all'istante t= 0, nella posizione 1. Nella 4), sostituendo quanto dedotto e il termine
permanente, calcolato al punto c), si ottiene:
Per il calcolo della costante s si parte dall'equazione differenziale del circuito:
Sostituendo i valori trovati nei vari punti e sostituendoli nella 4) si ottiene:
L'equazione che descrive l'andamento della corrente in funzione del tempo deve essere
verificata per qualsiasi istante. Per verificare se tale legge descrive il circuito RL serie, si
considerino i tempi t = 0 e t molto maggiore della costante di tempo.
Seconda parte
Dopo un tempo sufficientemente lungo ( maggiore o uguale a 5 volte la costante di tempo
del circuito ), l'interruttore T viene spostato sulla posizione 2. Il circuito corrispondente è
mostrato in figura:
La f.e.m costante E viene esclusa, come mostra la figura. La legge di Ohm, quindi diventa
un'equazione differenziale omogenea del I° ordine a coefficienti costanti. Le fasi per lo studio
del transitorio, che porterà la corrente dal valore E/R a 0 saranno del tutto simili a quelle viste.
La corrente di estinzione del transitorio è data da :
Per verificare se tale legge descrive il circuito di estinzione del transitorio in un circuito RL
serie, si considerino i tempi t = 0 e t molto maggiore della costante di tempo del circuito.