UNIVERSITÀ DEGLI STUDI DI CATANIA
Facoltà di Ingegneria
Dipartimento Elettrico, Elettronico e Sistemistico
Corso di Misure Elettriche
Anno Accademico 2000-2001
Prof. Nicola Pitrone
Relazione su
METODI DI PONTE
Gruppo di lavoro:
Filippo Chimento
Francesco Conticello
Pasquale Di Maggio
Federico Giordano
Enrico Perez
Guido Vagliasindi
Gennaio 2001
Metodi di ponte
© ing.elettrics_2000/2001
Generalità:
A differenza del metodo voltamperometrico, che si basa su una relazione analitica
dipendente da grandezze diverse rispetto a quella da misurare, i metodi di ponte
prevedono dei procedimenti di confronto diretto fra grandezze fornendo così una
precisione di misura maggiore.
Il confronto fra le due grandezze avviene paragonandone gli effetti in modo da
raggiungere una condizione di equilibrio che consenta di stabilire una ben definita
relazione tra esse.
Nei circuiti elettrici il raggiungimento dell’equilibrio è indicato, nella maggior parte
dei casi, dall’annullarsi della corrente o della tensione in un ramo del sistema: da
questo deriva la denominazione “metodi di zero”.
Per i metodi di confronto si richiedono dunque:
§ Una grandezza di riferimento (campione) da confrontare con la grandezza
incognita.
§ Degli organi di regolazione che consentono di raggiungere l’equilibrio.
§ Un rivelatore di zero, che altro non è che un rivelatore della condizione di
equilibrio del sistema1.
Sensibilità
Un ruolo fondamentale in ogni metodo di zero è ricoperto dal fattore sensibilità.
Questo perché e interessante valutare entro quali limiti di incertezza può considerarsi
realizzato l’equilibrio.
dx
della grandezza incognita
Occorre dunque valutare la minima variazione relativa
x
che si è in grado di percepire attorno ad una apparente condizione di equilibrio. Tale
variazione corrisponde appunto alla sensibilità σ e si esprime in percentuale.
La misura della sensibilità si può eseguire facilmente, dopo avere raggiunto
l’equilibrio e avere ottenuto un certo valore x della grandezza da misurare. Dando,
infatti, un incremento noto ∆x alla x si nota una deviazione ∆λ sul rivelatore di zero.
Detta quindi dλ la minima deviazione percettibile da tale rivelatore si può scrivere la
proporzione:
dx ∆x
:
= dλ : ∆ λ
x x
Da cui deriva la relazione:
σ=
dx dλ ∆x
=
x ∆λ x
1
un qualunque strumento richiede però un valore minimo di segnale (corrente o tensione) per dare luogo ad una
indicazione percettibile: la condizione di equilibrio sarà quindi apparentemente soddisfatta con un errore funzione delle
caratteristiche dello strumento stesso.
2
Metodi di ponte
© ing.elettrics_2000/2001
Nel caso di ponte in equilibrio posso allora sostituire a
di sensibilità per la data misura:
σ=
∆x
∆c
il
ottenendo il valore
x
c
∆c dλ
c λ
dove λ rappresenta la più piccola variazione percettibile sulla scala dello strumento
ed è detta dunque risoluzione di questo.
Posso allora determinare la sensibilità stabilendo la precisione percentuale:
δ x % = δ a % + δb % + δ c % ± σ
dove la sensibilità deve essere tale da non influenzare la precisione.
Metodo di sostituzione
In tutti i metodi di confronto, dunque, quando sia raggiunta la condizione di
equilibrio si ottiene una relazione fra la grandezza incognita e le grandezze note:
x = f (a, b, c,....., n)
Se, dopo avere ottenuto l’equilibrio, si sostituisce alla grandezza x un’altra y, ad
essa omogenea, nota e variabile, lasciando immutate le altre (a, b, c….), l’ equilibrio
si otterrà per quel valore yo di y per cui è:
y0 = f (a, b, c,........., n)
e sarà perciò:
x = y0
Questo procedimento è detto metodo di sostituzione.
3
Metodi di ponte
© ing.elettrics_2000/2001
Metodi di ponte in continua e in alternata
Sebbene i metodi di ponte in cc si possano ritenere dei casi particolari dei ponti in
ca, questi ultimi presentano delle caratteristiche particolari che li rendono meno
precisi e più complessi rispetto ai primi.
In primo luogo, poiché non esistono campioni di f.e.m. alternata, non sono possibili
misure di tensioni o correnti per confronto con i riferimenti assoluti. In secondo luogo
gli strumenti rivelatori di zero per alternata sono molto meno sensibili rispetto ai
corrispondenti in continua. Infine le relazioni di equilibrio in ca devono tenere conto
di grandezze variabili sia in modulo che in fase e quindi è richiesta sempre la
regolazione di due parametri (anziché uno solo) tra di loro indipendenti.
Di conseguenza le misure coi metodi di ponte in alternata vanno fatte fino ad un
determinato valore di frequenza ( ≤ 10Mhz ) oltre al quale si richiedono metodi ed
apparecchiature del tutto particolari.
METODI DI PONTE IN CORRENTE CONTINUA
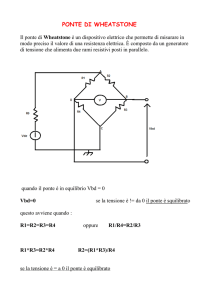
Il ponte di Wheatstone
Il ponte di Wheatstone rappresenta uno dei metodi più
antichi e diffusi per la misura di una resistenza:
l’incognita viene confrontata con una resistenza nota c,
mediante la regolazione di due resistori variabili a e b. Il
ponte si dice in equilibrio quando è nulla la corrente
nella diagonale CD. Fra i valori dei resistori del circuito
sussiste allora la relazione:
a
x= c
b
Infatti si ha:
I1 = I 2
⇒
bI 1 = cI 2
aI 1 = xI 2
⇒
Figura 1: ponte di Wheatstone
a
x= c
b
Tale condizione di equilibrio è indipendente sia dal valore della tensione di
alimentazione che da quelli delle resistenze delle diagonali AB e CD: essa resta
inalterata se si scambiano fra loro i due lati opposti o se si inverte la funzione delle
diagonali, spostando cioè il rivelatore di zero in AB e l’alimentazione in CD.
IL valore della resistenza x, fra i punti di contatto A e D, comprende sia le resistenze
di contatto in serie con l’incognita, sia le resistenze di dispersione, ad essa in
parallelo; il ponte risulta dunque adatto alla misura di resistenze dell’ ordine
1Ω ≤ R ≤ 10 5 Ω .
4
Metodi di ponte
© ing.elettrics_2000/2001
L’equilibrio si può ottenere equivalentemente:
a
§ Mantenendo costante il valore e variando c.
b
§ Mantenendo costante c e variando il rapporto fra a e b.
Precisione del metodo di ponte
L’errore relativo da cui è affetto il valore della resistenza x vale:
dx da db dc
=
−
+
±σ
x
a
b
c
L’ultimo termine di sensibilità esprime il limite di incertezza dato dal rivelatore di
zero e si verifica sperimentalmente.
Esiste un caso particolare in cui i lati a e b sono costituiti da un unico filo calibrato
di resistenza totale r, per cui:
a
a
=
b r−a
e l’errore relativo è dunque:
da db
1
rda
1
−
= da +
=
a
b
a r − a a(r − a)
che ha un minimo quando il denominatore è massimo cioè per a = b =
r
.
2
Un metodo efficace per diminuire l’influenza degli errori propri dei lati del ponte è
quello di sostituzione.
Si abbia infatti per un equilibrio, quando su AD è inserita la resistenza y:
a
y= c
b
con un secondo equilibrio, sostituendo la x alla y sul lato dell’incognita, si ottiene:
a ∆c
∆c
x = c 1 +
= y 1 +
b
c
c
∆c
x
è minore dell’errore sulla c se è
<< 1 , cioè se x e y
c
y
hanno pressoché lo stesso valore.
L’errore sul rapporto
5
Metodi di ponte
© ing.elettrics_2000/2001
Un ulteriore metodo, detto della “doppia pesata”, consiste nell’eseguire due
equilibri, scambiando fra di loro i lati a e b ottenendo:
a
x= c
b
b
b ∆c
x = c ' = c 1 +
a
a
c
∆c
∆c c + c '
⇒ x = c 2 1 +
≅ c 1 +
=
c
2c
2
e l’errore di misura in tal caso è dato da:
dx dc
=
±σ
x
c
Determiniamo analiticamente la sensibilità del ponte di Wheatstone:
Il risultato che otterremo sarà utile per stabilire quale tipo di galvanometro si deve
adottare per la misura.
Riduciamo il ponte al suo circuito equivalente
supponendolo alimentato da una tensione costante E, con
resistenza interna nulla. La f.e.m. a vuoto risulta:
b
c
∆E = E
−
c + x a + b
che non è altro che lo squilibrio ai capi della diagonale di
rivelazione BD.
Figura 2: circuito equivalente
Se, allora, desideriamo aumentare la sensibilità del ponte, agiamo tramite un
incremento della resistenza c, così da ottenere:
dE
c+ x−c
x
∆E = 0 ∆c = E
∆c = E
∆c
2
dc
(c − x )
(c − x )2
x
∆c
c
⇒ ∆E = E
2
x c
1 −
c
Allo stesso modo otteniamo la
resistenza interna del generatore
equivalente:
xc
ab
(x + a )c
Ri =
+
=
x+c a+b
x+c
Figura 3: resistenze equivalenti
6
Metodi di ponte
© ing.elettrics_2000/2001
A questo punto è immediato il calcolo della corrente che fluisce nel rivelatore di zero
e precisamente essa è:
∆E
Im =
Ri
che dipende dal valore
∆c x x
, e .
c c a
Doppio ponte
Nella misura di valori di resistenze inferiori a 10Ω diventa importante il ruolo
giocato dalle resistenze di contatto, per cui il metodo di ponte di Wheatstone diventa
insufficiente per ottenere una buona precisione.
Per eliminare tale effetto dei contatti si fa allora ricorso al doppio ponte detto anche
ponte di Thompson che è costituito da resistori a 4 morsetti. Lo schema di tale ponte
si riconduce al caso del ponte di Wheatstone tramite una trasformazione triangolo –
stella.
La condizione di equilibrio è dunque:
ra '
a
rb'
x+
= c+
a '+b'+ r b
a '+b'+ r
a
rb' a a '
⇒x= c+
−
b
a '+b '+ r b b'
Se si realizza che :
a a'
a b
= ⇒ =
b b'
a ' b'
la condizione di equilibrio sarà identica al caso
del ponte di Wheatstone:
Figura 4: doppio ponte
a
x= c
b
Gli effetti delle resistenze di contatto tra x e l’alimentazione, sono eliminati se le
connessioni alle resistenze sono effettuate internamente ai contatti: una parte di
queste resistenze viene a fare parte del valore di r, che non interviene nelle condizioni
di equilibrio. Le resistenze di contatto verso a e a’ risultano in serie con resistenze di
valore medio (dell’ordine della decina di ohm) per cui hanno effetto trascurabile.
Il problema per la realizzazione della condizione è dato dalla presenza della
resistenza r del conduttore tra i morsetti c e x. Volendo trovare la condizione di
equilibrio, infatti, dobbiamo notare la presenza di un triangolo di resistenze a’, b’ ed
r.
7
Metodi di ponte
© ing.elettrics_2000/2001
Trasformiamo a stella: la nuova condizione di
equilibrio sarà:
a
x + p = (c + q )
b
s
a
a
x= c+ q− p
b
b
p
q
E’ importante quindi che si realizzi la condizione su p
e q (che contengono r):
a
q− p=0
b
Figura 5: trasformazione a stella
Per mettere in evidenza l’effetto dato dalla presenza delle resistenze di contatto tra x
e c apriamo il circuito in corrispondenza di r ottenendo lo squilibrio:
b' r a a'
lim
r →
∞
− = b'
a'+b'+ r b b'
che non è altro che il valore di cui è opportuno correggere lo squilibrio.
Andiamo a vedere ancora come scegliere il galvanometro in base ai valori delle
resistenze.
Se diamo una piccola variazione alla x spostando l’equilibrio del ponte possiamo
osservare come le correnti che circolano nel circuito siano tutte molto piccole per cui
è lecito considerare in corrispondenza della variazione, un circuito equivalente cin
una generatore di tensione del valore ∆xI .
Il circuito da considerare allora diventa quello di figura 6 la cui diagonale di
rivelazione (comprensiva della resistenza interna dello strumento rg) vede il circuito
equivalente di figura 7.
G
a
a'
Re q
b'
b
V eq
G
Figura 7: circuito equivalente
Figura 6
8
Metodi di ponte
© ing.elettrics_2000/2001
I parametri del circuito trasformato alla Thevenin sono:
a ' b'
ab
Req =
+
a '+b' a + b
b
Veq = ∆xI
a+b
Quello che si vuole ottenere è una variazione relativa della corrente rivelabile più
piccola della precisione dello strumento e quindi:
Veq
≤ precisione dello strumento
Re q + ∆x
METODI POTENZIOMETRICI
Il potenziometro è uno strumento che permette di effettuare misure con la precisione
del campione utilizzato. Tale metodo unisce in sé le caratteristiche di un metodo di
zero, di sostituzione e di confronto diretto. Poiché è possibile raggiungere sensibilità
molto elevate, il potenziometro si presta, ad esempio, per il confronto di f.e.m. e
cadute di tensione con le pile campioni, di pile campione fra di loro e per le tarature
degli strumenti in corrente continua.
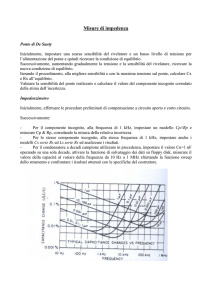
Potenziometro a corrente costante e misura diretta.
Tale tipo di potenziometro viene utilizzato per misurare un valore di tensione fornito
da un generatore e a questo scopo viene utilizzato come riferimento la pila campione.
Lo schema per la misura è il seguente:
A
R1
G
R2
Ec
Ex
Figura 8: potenziomentro a corrente costante
La tensione che viene usata per il confronto è quella ai capi di R2; Ec è la tensione
della pila campione ed Ex il valore della tensione da misurare.
La misura avviene nel seguente modo:
§ Si commuta l’interruttore su Ec e si regolano i resistori variabili fin quando il
galvanometro non segna lo zero di corrente.
9
Metodi di ponte
© ing.elettrics_2000/2001
§ Si valuta il valore della tensione erogata dal generatore campione: sia questa
per esempio:
Ec = 1.0564V
§ Si regolano i resistori R1 e R2, che sono cassette di resistenze a decadi, in modo
tale che la somma dei valori delle resistenze sulle decadi corrispondenti sia
uguale a 10 e che il valore del resistore R2 abbia i valori delle decadi
corrispondenti a quelle del generatore:
1
0
5
6
.4
R2
9
10
5
4
.6
R1
Figura 9: resistori a decadi
In tal modo si rende costante il valore di resistenza in tutto il circuito.
§ Si osserva che il valore di corrente per ottenere la tensione del campione deve
essere fissata, nel caso specifico I=1 mA. A tal fine si regolano la tensione di
alimentazione e la resistenza variabile a valle di essa.
§ Si commuta l’interruttore sulla tensione da misurare Ex.
§ Si fa variare il valore di R2 in modo tale da ottenere che la somma dei due
resistori sia sempre costante, finché non si ottiene nuovamente l’equilibrio.
§ La nuova lettura del valore di R2 all’equilibrio (spostando opportunamente il
valore della virgola) è il valore della tensione Ex, con la stessa precisione di
misura del campione.
Si può notare come nella prima fase della misura:
R2
VR 2 = E
= EC
R + R1 + R2
mentre nella seconda fase:
R' 2
V 'R 2 = E
= EX
R + R1 + R '2
da cui:
R
E X = EC 2 '
R2
10
Metodi di ponte
© ing.elettrics_2000/2001
Limiti della misura potenziomentrica
§ Le correnti erogate dalle pile campione restano costanti se poco intense e di
breve durata: poiché la misura potenziomentrica si basa proprio sulla
precisione del campione è opportuno fare scorrere nel circuito correnti
piccole.
§ La temperatura è una grandezza di influenza importante in quanto le
correnti basse possono facilmente essere influenzate da essa.
§ Per controllare se la corrente è rimasta costante bisogna ritornare nelle
condizioni precedenti: se il valore non è rimasto lo stesso si deve ripetere
l’esperienza.
APPLICAZIONI DEL METODO POTENZIOMENTRICO
Taratura degli amperometri
La taratura di un amperometro consiste nella determinazione dell’indice di classe di
questo e quindi dell’errore assoluto massimo
Il circuito di misura è tale che l’errore massimo è
dato dalla differenza tra il valore di corrente letto
sullo strumento e quello misurato dal rapporto tra la
tensione ai morsetti AB e la resistenza campione R:
E
ε max = I L − X
R
Figura 10: circuito di taratura per un
amperometro
Di conseguenza l’indice di classe sarà:
ε max
100[%]
P
La sorgente fornisce all’amperometro e al resistore R una corrente continua e
regolare: il valore di R è scelto in modo tale che la tensione applicata al
potenziometro risulto dell’ordine di 1 Volt, il che richiede, per correnti più elevate,
una notevole dissipazione di potenza.
n=
11
Metodi di ponte
© ing.elettrics_2000/2001
Taratura di un voltmetro
La taratura di un voltmetro risulta concettualmente e praticamente analoga a quella
per l’amperometro, con la piccola differenza che per tensioni più elevate di 1 Volt si
fa uso di un divisore di tensione (vedi appendice) all’ingresso del potenziometro.
Lo schema elettrico è il seguente:
Figura 11: circuito di taratura di un voltmetro
Taratura di un wattmetro
La taratura di un wattmetro si esegue , banalmente, dalla combinazione degli schemi
di taratura dei voltmetri e degli amperometri. I circuiti di tensione sono separati in
modo che la potenza segnata dallo strumento non crei problemi di dissipazione
termica o di eccessivo consumo.
Figura 12: schema di taratura del wattmetro
12
Metodi di ponte
© ing.elettrics_2000/2001
APPENDICE
Divisori di tensione
Dispositivo di Kelvin Varley
Il dispositivo di Kelvin Varley serve per potere ottenere un valore di resistenza di
valore costante è molto preciso.
Figura 13: dispositivo di Kelvin Varley
Esso è formato da undici resistenze di valore R a cui viene applicata una tensione V e
da un cursore costituito da un resistore di valore 2R che si mette in parallelo a due
delle resistenze fisse per ottenere un valore totale 10 R.
Prelevando allora la tensione ai morsetti AC”, a seconda del punto in cui si trova il
cursore, si possono prelevare tensioni che vanno da 0 a 9/10 di V.
La precisione può essere ovviamente aumentata (nei limiti imposti dalle
caratteristiche dei resistori) inserendo al posto del cursore di valore 2R, un cursore di
uguale valore ma suddiviso in 10 resistori del valore R/5 a cui a sua volta è collegato
un altro resistore variabile del valore 2R/5. La precisione così ottenuta è di 1/100 di
V.
Un altro dispositivo divisore usato per ottenere valori di tensione precisi è il seguente:
Figura 14
Esso permette di ottenere dalla commutazione del tasto in B’ una tensione pari a V tra
il morsetto C e massa, mentre se l’interruttore chiude su B il valore di E raccolto alla
stessa porta è di 1/100 V.
13
Metodi di ponte
© ing.elettrics_2000/2001
Ponti in corrente alternata.
I ponti in corrente alternata si classificano in due grandi categorie:
1. PONTI A FREQUENZA INDUSTRIALE, usati nel campo delle frequenze acustiche,
all’incirca da 50Hz a 1kHz;
2.
PONTI A RADIOFREQUENZA,
usati a frequenza superiori a 1kHz;
Prima di fare qualunque discettazione in merito, occorre tenere sempre presente la
frequenza alla quale si sta effettuando la misura, perché i componenti utilizzati nel
circuito non sono ideali e cambiano la loro caratteristica al variare di questa.
Un altro aspetto da tenere in considerazione è il rumore, che può falsare la misura;
per evitarne gli effetti, si usano cavi schermati, come si fa con gli oscilloscopi, ma
non sempre è possibile eliminare totalmente il rumore.
I COMPONENTI UTILIZZATI SONO:
•
CAPACITORI VARIABILI:
•
INDUTTORI:
presentano sempre una certa resistenza, e una certa capacità, cose che
li allontanano molto dall’essere considerati un componenti ideali; addirittura, alla
frequenza di risonanza, reattanza induttiva e capacitiva si eguagliano e l’induttore
ha un comportamento puramente resistivo. Inoltre gli induttori avvolti su un
nucleo ferromagnetico presentano perdite per isteresi e per correnti parassite, così
si preferisce usare le FERRITI, che riducono di molto queste perdite, oltre a rendere
più lineare il comportamento del componente, in quanto le ferriti hanno
permeabilità magnetica relativa pressoché costante.
•
RESISTORI VARIABILI:
sono quelli che più si avvicinano all’idealità; in
radiofrequenza si utilizzano capacitori campione in aria, la cui capacità è variabile
con la distanza fra le armature, che sono piane e parallele;
per le frequenza acustiche si usano resistori variabili che
vanno da pochi Ω al kΩ; questi però non vanno più bene a frequenze elevate
perché introducono molto rumore nel circuito di misura;
In questa sede si prenderanno in esame solo i ponti utilizzati nel campo delle
frequenze acustiche.
14
Metodi di ponte
© ing.elettrics_2000/2001
Ponti in corrente alternata a frequenza industriale.
I ponti utilizzati in corrente alternate sono a 4 o più lati, a seconda della dinamica che
si vuole ottenere, ma anche a seconda della natura e dell’entità della grandezza che si
vuole misurare. Lo schema generale di un ponte in corrente alternata è il seguente:
Z
Z
1
2
Rivelatoredi Zero
Z3
Z4
Figura 15: Schema generale di un ponte in corrente alternata
Sulla diagonale di rivelazione non si mette un semplice galvanometro, ma un
rivelatore di zero particolare, che deve lavorare bene ad una ben fissata frequenza. Le
sue caratteristiche fondamentali sono:
• SELETTIVITÀ: è la capacità nel distinguere i segnali a in base alla loro frequenza
ed è molto importante perché elimina l’effetto delle armoniche della grandezza da
misurare, armoniche spesso dovute a rumore; talvolta, per limitare le correnti di
rumore, si usa il dispositivo detto “Terra di Wagner”, il cui scopo è far si che il
rumore non passi dalle impedenze del circuito di misura, ma da altre vie; se il
rivelatore di zero è collegato tra i morsetti A e B, vede le impedenze Z1, Z2, Z3, Z4;
A
Z
Z
1
2
Rivelatore di Zero
Z3
R
B
Z4
RB
A
Figura 16: Dispositivo di Wagner
15
Metodi di ponte
© ing.elettrics_2000/2001
Se invece viene collegato tra A e la terra, vede le impedenze Z1, Z2, RA, RB, e per
equilibrare il nuovo ponte che si ottiene, si gioca su RA e RB. Realizzati gli
equilibri di entrambi i ponti, accade che sui due condensatori centrali non passa
alcuna corrente. Invece le correnti sui due esterni vanno all’alimentatore e non
interessano il circuito di misura.
• SENSIBILITÀ: è la minima variazione relativa della grandezza incognita che si è in
grado di percepire intorno ad una apparente condizione di equilibrio; misurata la
grandezza incognita x, la si incrementa di una quantità nota ∆x, e si vede quanto
vale i valore della deviazione ∆λ del rivelatore di zero; quindi se dλ è la minima
deviazione percettibile di detto strumento, si definisce sensibilità σ il seguente
rapporto:
σ=
dλ ∆x
⋅
;
∆λ x
In genere i rivelatori di zero sono caratterizzati da una frequenza di massima
selettività e sensibilità, e due sono quelli più interessanti:
• ORECCHIO UMANO: associato ad un trasduttore che converta il segnale elettrico in
segnale acustico per mezzo di un amplificatore ad alto guadagno e a banda passate
stretta (perché la frequenza non può variare molto), è il rivelatore che riesce a
cogliere segnali di piccola potenza e a frequenza elevata;
• ELETTRODINAMOMETRO: è un wattmetro elettrodimanico fatto per correnti molto
piccole; si usa a 50Hz, e per sua costituzione risulta essere sensibile e selettivo;
• GALVANOMETRO A VIBRAZIONE: è uno strumento fatto in modo da avere un
momento di inerzia bassissimo in modo tale da riuscire a seguire tutte le
vibrazioni; è costituito da un circuito risonante che lavora a frequenza superiore a
quella di risonanza;
All’equilibrio si ha:
Z1
⋅ Z 4 , ovvero Z 3 = Z1 ⋅ Z 4 ⋅ Y2 ;
Z2
I ponti si classificano anche in
• Ponti a Rapporto: un ponte si dice a rapporto quando le impedenze dei lati 1 e 2
sono elementi puri, in genere o due resistenze o due capacità campione;
• Ponti a Prodotto: si dice invece ponte a prodotto quello in cui i lati 1 e 4 sono
elementi puri;
in entrambi i casi si ricava anche l’equazione che dà la fase dell’impedenza incognita:
ϕ 3 = ϕ1 − ϕ 2 + ϕ 4 ;
Z3 =
16
Metodi di ponte
© ing.elettrics_2000/2001
da questa equazione si vede se l’impedenza è induttiva o capacitiva.
Si vedranno ora alcuni dei ponti più utilizzati per le misure di impedenze, a rapporto
e a prodotto. Della prima categoria sono i ponti di De Sauty, Gott e Wien; della
seconda quelli di Maxwell e Schering. Infine si vedrà il ponte universale.
Ponti a Rapporto:
Ponte di De Sauty
E’ un ponte a rapporto reale per la misura di capacità; lo schema circuitale è il
seguente:
R1
R2
G
Cx
C4
Figura 17: ponte di De Sauty
La relazione che permette di misurare la capacità Cx, all’equilibrio, è:
R
1
1 R1
; ⇒ C x = 2 C;
=
R1
jω C x
jωC R 2
quindi il valore di Cx prescinde dalla frequenza del generatore, infatti nella relazione
di equilibrio del ponte non compare.
Ponte di Gott
Però non si ha nessuna informazione sull’angolo di perdita del condensatore, di cui si
deve tenere conto; allora lo schema circuitale equivalente che più conviene è quello
di Gott, un ponte a rapporto reale: si devono inserire le resistenze R e Rx, che danno
l’angolo di perdita rispettivamente dei condensatori C e Cx:
17
Metodi di ponte
© ing.elettrics_2000/2001
R1
R2
G
Rx
C4
Cx
R4
Figura 18: ponte di Gott
in questo modo le relazioni cambiano:
Rx +
R
1
= 1
jωC x R 2
1
; ovvero:
R +
jωC
R1
R x = R R ;
2
C = R 2 C;
x R 1
moltiplicando membro a membro, si ottiene:
R x C x = RC ;
cioè l’angolo di perdita della capacità incognita si può calcolare a prescindere dalla
conoscenza di R1e R2, infatti:
tan δ x = ωR x C x = ωRC
Ponte di Wien
Si usa per la misura di induttanze per confronto con una campione; è un ponte a
rapporto reale, e dallo schema circuitale qui riportato
R1
R2
G
Rx
L4
Lx
R4
Figura 19: ponte di Wien
si può vedere che:
18
Metodi di ponte
© ing.elettrics_2000/2001
R x + jωL x =
R1
(R 4 + jωL 4 ) ; cioè:
R2
R 1R 4
R x = R ;
2
L = R 1 L ;
x R 2 4
inoltre, dividendo membro a membro, si ricava l’angolo di perdita dell’induttanza a
prescindere dai valori di R1 e R2:
Lx
L
= 4 .
Rx R4
Ponte di Owen
È un ponte a rapporto puramente immaginario il cui schema circuitale è il seguente:
R1
R2
G
Rx
Lx
C4
R4
Figura 20: ponte di Owen
Permette di determinare il valore di una induttanza per confronto con una capacità
campione, allora si ha:
1
, quindi:
R x + jωL x = jωR 1C 2 R 4 +
jωC 4
C2
R1;
R x =
C4
L = R R C ;
x
1 4 2
Ponti a Prodotto:
Ponte di Maxwell
È un ponte a prodotto reale, il cui schema circuitale è il seguente:
19
Metodi di ponte
© ing.elettrics_2000/2001
C2
R1
R2
G
Rx
R4
Lx
Figura 21: ponte di Maxwell
il generatore è sinusoidale e a 1000Hz;
In questo modo, la relazione tra l’impedenza incognita e i lati noti, all’equilibrio è:
1
R x + jωL x = R 1R 4
+ jωC 2
R2
Le resistenze e le capacità note sono campioni; la R2 e la C2 sono messe in parallelo
perché se fossero in serie i valori di reattanza che si otterrebbero non sarebbero
sufficienti a compensare il ponte, inoltre sarebbe fastidioso lavorare con la serie
piuttosto che col parallelo.
In questo modo è:
R 1R 4
;
R x =
R2
L = R R C ;
x
1 4 2
Un altro schema del ponte di Maxwell è il seguente:
R1
R2
G
2
1
Rx
Lx
R
L4
R4
Figura 22: ponte di Maxwell
in cui il commutatore serve a spostare la resistenza R su uno dei due lati, in modo da
avere costanti di tempo per le induttanze, quella nota e quella da misurare, uguali.
Se il commutatore è nella posizione 2, si ha:
20
Metodi di ponte
© ing.elettrics_2000/2001
R1
R
=
R C − R;
x
R2
R1
(R C + jωL C ); ⇒
R + R x + jω L x =
R2
L = R 1 L ;
x R 2 C
Invece sulla posizione 1 è:
R1
(R C + R );
R
=
x
R2
L = R 1 L ;
x R 2 C
Se R=0, accade che
R1
R
=
RC;
x
R2
L = R 1 L ;
x R 2 C
e dividendo membro a membro si ottiene:
L
Lx
= C;
Rx RC
cioè le costanti di tempo dei due lati induttivi devono essere uguali. Se questo non
accade, allora si ricorre alla R, mettendola sul lato opportuno per mezzo del
commutatore e regolandola in maniera adeguata, in modo che sia realizzata la
suddetta condizione.
Come visto nei precedenti casi, sarà possibile calcolare l’angolo di perdita
dell’impedenza incognita.
Ponte di Schering
Lo schema circuitale è il seguente:
C2
R1
G
Rx
Cx
R2
C4
Figura 23: ponte di Shering
21
Metodi di ponte
© ing.elettrics_2000/2001
È un ponte a prodotto puramente immaginario e si usa per misurare impedenze per
confronto con una capacità campione:
Rx +
1
+ jωC 2 ; cioè:
R2
C2
R x = C R 1 ;
4
C = R 2 C ;
x R 1 4
R1
1
=
jωC x jωC 4
e per quanto riguarda l’angolo di perdita:
R xC x = R 2C2 .
Ponte Universale
È quello che meglio si adatta a tutte le situazioni, e lo schema è:
C2
R1
R2
G
R3
C4
C3
Figura 24: ponte universale
La relazione che permette il calcolo dell’impedenza incognita è:
1
1
= − jR 1
R '3 + R x + j ωL x −
ωC 3
ωC 4
1
' + jωC 2 ;
R2
cioè:
C2
'
R x = C R 1 − R 3 ;
4
ωL = 1 − R 1 ;
x ωC 3 ωC 4 R '2
Se però non c’è alcuna impedenza da misurare, il ponte deve comunque essere in
equilibrio, cioè
R3 −
j
1
= − jR 1
ωC 3
ωC 4
1
+ jωC 2 ;
R2
cioè:
22
Metodi di ponte
© ing.elettrics_2000/2001
C2
R
=
R1;
3
C4
C = R 2 C ;
3 R 1 4
questi risultati, sostituiti nella precedente relazione di misura, danno:
R x = R 3 − R '3 ;
R1 1
1
ωL x = ωC R − ' ;
R2
4
2
23
Metodi di ponte
© ing.elettrics_2000/2001
LABORATORIO SUI METODI DI PONTE
Ponti in corrente alternata
Ponte di Maxwell
Abbiamo effettuato la misura di un induttanza realizzata mediante un avvolgimento
di rame su un nucleo di materiale ferromagnetico.
B
A
Per effettuare tale misura lo schema di ponte
utilizzato è stata quella del tipico ponte di
Maxwell con un resistore a cassetta dotato
delle regolazioni su A e B e sulla resistenza R
che, mediante la commutazione del tasto T,
va a sommarsi all’induttanza campione o a
quella incognita.
G
2
1
Lx
Rx
R
Lc
Rc
Figura 25: ponte di Maxwell
I dati di targa della strumentazione e dei campioni utilizzati è la seguente:
Generatore per conti in corrente alternata: TIPO G.P.2
Galvanometro: indice di classe [n]= 1.5
Vmax=2V
Induttanza campione: L=0.01H
Imax=1.5mA
Rint=
Consideriamo inizialmente il tasto in posizione 1 e teniamo conto della presenza di
resistenze parassite sia per il campione sia per l’induttanza incognita.
All’equilibrio sarà:
jωL x + R x =
A
( jωLc + Rc + R )
B
Ovvero eguagliando parte reale ed immaginaria:
A
R x = B (Rc + R )
ωL x = A ωLc
B
Scegliamo per il galvanometro il valore di sensibilità più basso (1\100) e procediamo
per tentativi per realizzare l’annullamento della corrente nella diagonale di
rivelazione.
24
Metodi di ponte
© ing.elettrics_2000/2001
Otteniamo valori prossimi all’equilibrio fissando la resistenza B al valore di 100 Ω e
regolando il resistore A su ordini di grandezza prossimi compresi tra i 7 KΩ e 5 KΩ .
Procediamo aumentando il livello di sensibilità ad 1/10 e i valori per l’equilibrio si
spostano verso il valore di A (sempre tenendo fissato B al valore di 100Ω ) per valori
prossimi ai 7 KΩ .
A questo punto facciamo l’ultima prova a sensibilità σ = 1 e troviamo che il valore di
A per l’equilibrio si assesta sul valore 7500 Ω .
Commutiamo a questo punto l’interruttore in posizione 2 e ripetiamo l’esperienza
giocando anche sul dispositivo a terra di Wagner, di cui lo strumento è dotato, e sulla
sensibilità del generatore stesso. Dopo avere effettuato tale bilanciamento per
avvicinarci all’equilibrio sfruttiamo la resistenza R portandola al valore di 100 Ω .
Osserviamo però immediatamente che lo strumento indicatore si allontana dalla
posizione di zero per cui diminuiamo il valore di R fino ad ottenere il risultato
ottimale al valore di R = 0.6Ω (cioè praticamente un valore trascurabile) ed
effettuando la regolazione fine sul galvanometro.
Verifichiamo infine se l’equilibrio si mantiene riportando il tasto in posizione 1: per
portare lo strumento allo zero effettuiamo una correzione finale sul valore di A che
viene stabilito definitivamente al valore di 7590 Ω .
I valori per l’equilibrio sono in definitiva:
A = 7590ΒΩ
B = 100Ω
Lc = 0.01H
R = 0.6Ω
Trascurando la resistenza dell’induttanza campione i valori di resistenza e di
induttanza incognite sono:
A
7590
0.6 = 45.54Ω
Rx = R =
B
100
A
7590
Lx = Lc =
0.01 = 0.759 H = 759mH
B
100
25
Metodi di ponte
© ing.elettrics_2000/2001
Ponte universale
In laboratorio è già predisposta un’apparecchiatura che costituisce il ponte
universale per la quale è già soddisfatta la condizione di equilibrio preliminare. In
essa tutti i collegamenti sono già predisposti e l’unica operazione da fare è dunque
inserire l’elemento da misurare e quindi portare il ponte, in questa sua nuova
configurazione, all’equilibrio, così come del resto si prevede che si operi. Lo schema
di misura su cui operare è il seguente:
Procediamo dapprima con la determinazione del valore di un’induttanza. La
colleghiamo pertanto ai morsetti di test, avendo prestato in precedenza attenzione a
azzerare tutti gli indicatori. Posizioniamo l’indicatore del tipo di elemento da testare
sull’indicazione di induttanza e procediamo preventivamente a determinare,
mantenendo per ora al minimo la sensibilità, l’ordine di grandezza dell’elemento in
prova, ricercando quell’ordine per il quale l’indicazione del rivelatore di zero fosse la
più vicina allo zero stesso. Rileviamo dunque che l’induttanza in gioco è dell’ordine
dei µH . Procediamo a questo punto alla stima del suo valore esatto. L’operazione si
svolge nel modo seguente: ruotiamo le manopole degli indicatori delle unità, decine e
centinaia di µH . Ogni volta che otteniamo sull’indicatore lo zero aumentiamo la
sensibilità dello strumento, allo scopo di ottenere una misura accurata. Nello stesso
tempo cerchiamo di bilanciare le perdite (che ovviamente esistono in quanto
l’induttanza è reale, per cui essa presenterà un cetra resistenza che darà luogo a
dissipazione per effetto Joule). Procedendo in questo modo arriviamo al massimo
della sensibilità in corrispondenza della quale otteniamo un valore di
L=174 µH
Con un fattore di bontà Q=1.2.
26
Metodi di ponte
© ing.elettrics_2000/2001
Procediamo successivamente alla misura di una capacità campione del valore di
0.0.1 µF e massima tensione sopportabile 500V. Dopo aver portato nuovamente tutti
gli indicatori a zero ruotiamo la manopola relativa al tipo elemento in prova
sull’indicazione capacità e procediamo come nel caso precedente. Troviamo un
ordine di grandezza dei nF e una stima iniziale di circa 9 nF. Facciamo ora in modo
di ottenere un maggior numero di cifre significative ruotano un’opportuna manopola.
Procedendo esattamente come sopra troviamo un valore di capacità pari a
C=9.95 nF
Priva di perdite. Questa rappresenta una buona misura della capacità in questione se
teniamo conto che abbiamo operato non usando cavetti schermati e con un rivelatore
di zero non perfettamente funzionante.
Osserviamo ancora che l’indicazione sul rivelatore di zero è fortemente falsata se
viene toccato l’involucro esterno della capacità campione. Tale effetto si riduce se
colleghiamo anche la massa tra la capacità e il ponte.
LABORATORIO SUI POTEZIOMETRI
Potenziometro a corrente continua e misura diretta.
Eseguiamo la misura su una pila campione del valore di targa di 1.01858 V facendo
uso di due cassette resistori a decadi.
Facciamo uso del seguente schema elettrico:
A
R1
G
R2
Ec
Ex
Figura 26: potenziometro a corrente continua e lettura diretta
Regoliamo dunque il valore del resistore R2 a 10185.8 Ω e il resistore R1 in modo
complementare ossia pari a 100925.2 Ω dove si è riportata una cifra nella penultima
decade.
Facciamo in modo che nella maglia principale circoli una corrente I = 100 µA ,
variando opportunamente il valore della resistenza variabile R’ di valore massimo
27
Metodi di ponte
© ing.elettrics_2000/2001
10k Ω e mantenendo costante il valore di R1+R2=1111108 Ω e portando la tensione
del generatore di costante a 11.5V.
A questo punto osserviamo come la tensione ai capi della resistenza campione è pari
a quella ai capi del resistore R2. Otteniamo l’equilibrio per valori di sensibilità
decrescenti regolando il valore del resistore variabile R’ in modo opportuno.
Spostiamo ora il commutatore sulla pila di valore incognito che è una pila a piattina
di valore nominale di 9V, ma piuttosto scarica.
Mantenendo sempre costante il valore di R1+R2 regoliamo il valore della R’ in modo
tale da ottenere la corrente nella maglia principale pari sempre a 100 µA .
A questo punto procediamo per tentativi variando il valore dei resistori
complementari fino ad ottenere l’equilibrio: partiamo dunque dal valore di R2 pari a
90000 Ω e notiamo subito uno squilibrio positivo.
Agiamo per tentativi fino al valore di 60721.0 Ω , valore per il quale il galvanometro
segna con precisione lo zero.
Poiché il metodo è a lettura diretta è il circuito è all’equilibrio osserviamo
immediatamente come il valore definitivo di Ex è dato dal nuovo valore della
resistenza R2 all’equilibrio moltiplicato per il valore della corrente (10^-4) ed è
quindi, in definitiva, di 6.07210V.
28
Metodi di ponte
© ing.elettrics_2000/2001