Corso di Fisica AA 2011-2012
Cap.3
Cap.3: Cinematica (II)
Moto Curvilineo
Il moto è curvilineo quando la traiettoria non è una linea retta.
sx
In questo caso, la posizione di un punto sulla traiettoria è indicata da un vettore s= s y .
sz
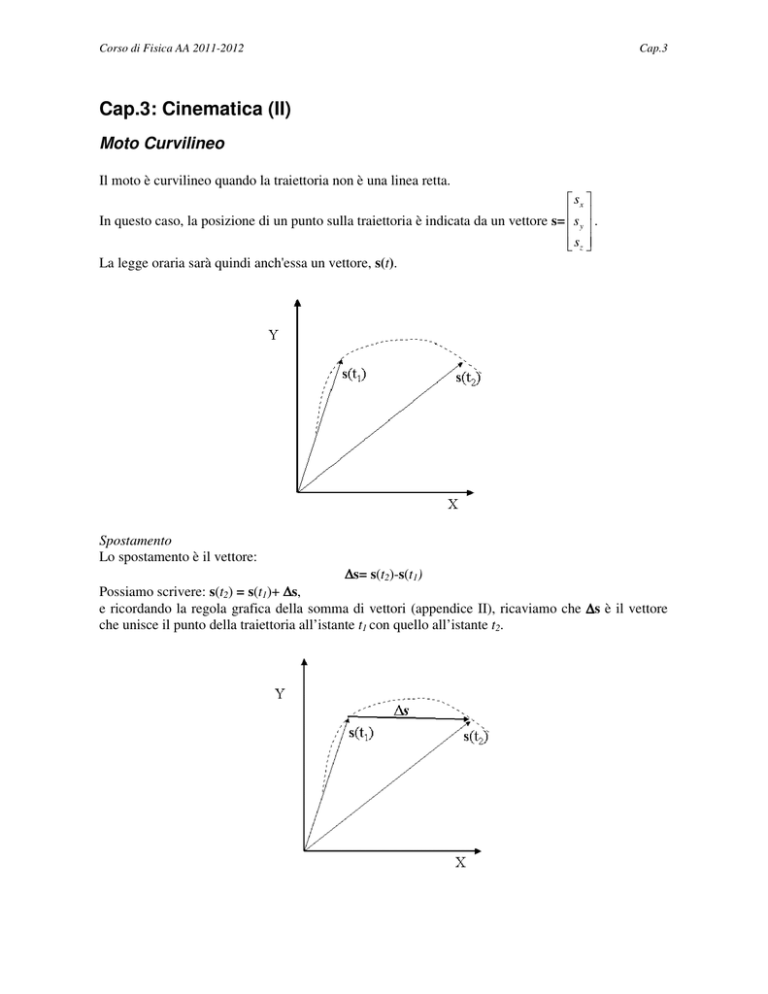
La legge oraria sarà quindi anch'essa un vettore, s(t).
Spostamento
Lo spostamento è il vettore:
∆s= s(t2)-s(t1)
Possiamo scrivere: s(t2) = s(t1)+ ∆s,
e ricordando la regola grafica della somma di vettori (appendice II), ricaviamo che ∆s è il vettore
che unisce il punto della traiettoria all’istante t1 con quello all’istante t2.
Corso di Fisica AA 2011-2012
Cap.3
Velocità media.
s(t ) − s(t1 ) ∆s
=
Vm(t1,t2)= 2
∆t
t 2 − t1
Velocità istantanea.
∆s
∆t
Come si vede dalla figura, la velocità istantanea è un vettore tangente alla traiettoria.
v(t)= lim ∆t →0 Vm (t , t + ∆t ) = lim ∆t →0
Accelerazione media
v (t 2 ) − v (t1 ) ∆v
Am(t1,t2)=
=
t 2 − t1
∆t
Accelerazione istantanea
a(t)= lim ∆t →0 Am(t,t+∆t) = lim ∆t →0
∆v
∆t
Come si vede dalla figura, l’accelerazione istantanea è un vettore diretto verso l’interno della
traiettoria.
Corso di Fisica AA 2011-2012
Esempio 1. Un ciclista pedala su una pista circolare di 1000 m
di diametro con velocità in modulo costante. All’istante t=0 s
passa sotto la linea del traguardo (P) e percorre un giro di
pista in 4 minuti. Indicare modulo e direzione della velocità
media:
A) dopo 1 minuto;
B) dopo 2 minuti;
C) dopo 3 minuti;
D) dopo 4 minuti.
Indicare inoltre la velocità istantanea.
Cap.3
A
P
B
C
A) Dopo 60 s ha percorso ¼ di pista e si trova in A. Il vettore ∆s =s(60)-s(0) è diretto a 45° ; il raggio della
circonferenza è 500 m e quindi per il teorema di Pitagora |∆s| vale:
| s (60) − s (0) |= 500 2 + 500 2 = 707 m
Il vettore velocità media è diretto come ∆s e in modulo vale |Vm|=707/60=11,78 m/s
B) Dopo 120 s si trova nel punto B. Allora ∆s =s(120)-s(0) è un vettore orizzontale di modulo=1000 m. Il
vettore velocità media è anch’esso orizzontale e vale in modulo: | Vm |=1000/120=8,3 m/s
C) Dopo 180 s si trova in C. Allora ∆s =s(180)-s(0) è diretto a –45°, ed in modulo vale 707m.
|Vm |=707/180=3.9 m/s
D) Dopo 240 s si ritrova al punto di partenza, il vettore ∆s ha modulo=0 e quindi |Vm |= 0.
E) La velocità istantanea è un vettore tangente alla circonferenza (la direzione varia istante per istante), di
modulo costante e pari a: |v|=1000π/240=13.09 m/s (47,1 km/h)
I vettori velocità media sono disegnati qui sotto a sinistra; i vettori velocità istantanea a destra.
A)
B)
C)
Corso di Fisica AA 2011-2012
Cap.3
Moto curvilineo nel piano: moto ad accelerazione costante
In questo caso a(t)=a, cioè l’accelerazione è un vettore costante. Sono allora costanti le componenti
ax e ay:
a x
a=
a y
Scomponiamo il moto nelle componenti x e y, e troviamo le componenti x e y dei vettori velocità
v x (t )
s x (t )
e legge oraria s(t)=
v(t)=
. Le espressioni sono simili a quelle del moto rettilineo
v y (t )
s y (t )
uniformemente accelerato:
ax t + v0 x
v(t)=
a y t + v0 y
1 a t 2 + v t + s0 x
s(t)= 12 x 2 0 x
2 a y t + v0 y t + s0 y
Questo è il moto caratteristico di un proiettile (ad esempio, di una palla calciata, di un peso lanciato,
di una rana che salta, ecc).
Applicazione del moto uniformemente accelerato nel piano: Moto di un proiettile
Facciamo l'ipotesi di:
1) trascurare la resistenza dell'aria;
2) considerare costante il vettore accelerazione di gravità g.
Prendendo l'asse X orizzontale e Y verticale orientato verso l'alto, avremo:
a x 0
a= = ;
a y − g
Y
↓g
X
e quindi il moto complessivo è composto dalla sovrapposizione di un moto orizzontale rettilineo
uniforme e di uno verticale rettilineo uniformemente accelerato.
v x ( t )
v(t)=
=
v y ( t )
s x ( t )
s(t)=
=
s y ( t )
v0 x
− gt + v ;
0y
v0 xt + s0 x
− 1 gt 2 + v t + s
0y
0y
2
Scomporre il moto nel piano nelle due componenti verticali e orizzontali permette di risolvere in
modo intuitivo problemi apparentemente complessi. Consideriamo i seguenti due esempi:
Corso di Fisica AA 2011-2012
Cap.3
Esempio 1. Due palle sono lanciate da una finestra: la prima è lasciata cadere da ferma, la
seconda è lanciata con una grossa spinta in avanti. Quale delle due arriva prima a terra?
La componente verticale del moto è la stessa e le palle toccano terra contemporaneamente. La foto
ad esposizione multipla mostra le due traiettorie: istante per istante l'altezza da terra è la stessa.
Esempio 2. Un cannoncino giocattolo spara un proiettile contro un orsacchiotto appeso al muro. A
che angolo bisogna alzare la canna del cannone per colpire il bersaglio se l'orsacchiotto viene
sganciato nell'istante in cui il cannone spara?
In assenza di gravità, il proiettile viaggerebbe in linea retta e l'orsacchiotto non si muoverebbe. In
questo caso bisogna puntare direttamente al bersaglio. In presenza di gravità, sia l'orsacchiotto che
il proiettile "cadono" della stessa quantità muovendosi verso il basso con la stessa legge oraria. Non
è quindi necessario cambiare l’angolo della canna. L'effetto della gravità è solo quello di fare
incontrare proiettile e bersaglio un po' più in basso.
Corso di Fisica AA 2011-2012
Cap.3
Esempio 3. Servizio a TENNIS
Una palla da tennis è battuta orizzontalmente da un'altezza di 2.5 m, alla velocità di 30.5 m/s.
La rete è lontana 12.2 m dal battitore, ed è alta 90 cm.
La palla toccherà la rete?
A che distanza andrà cadere?
s0
V0
?
0
s0=
2.5
30.5
V0=
0
La componente orizzontale del moto della palla è un moto rettilineo uniforme, quella verticale è un
moto rettilineo uniformemente accelerato.
La legge oraria è quindi:
v0 x t + s0 x
30.5t
s(t)= 1 2
=
2
−
gt
+
v
t
+
s
0y
0y
−4.9 × t + 2.5
2
La palla raggiunge la verticale della rete quando sx(t)=12.2
cioè quando
30.5t=12.2
o
t=0.4 s
In questo istante l'altezza della palla è:
sy(0.4)= -4.9×(0.4)2+2.5=1.7 m
Poiché la rete è alta solo 0.9 m, la palla sorvola la rete.
La palla tocca terra quando sy(t)=0.
Quindi quando
Risolvendo otteniamo
-4.9t2+2.5=0
t2=0.51
t=0.714 s
(Quiz: perché scartiamo la soluzione negativa t= -0.714 s?)
Per trovare la posizione orizzontale della palla, basta calcolare sx(t)=v0xt nell’istante t=0.714.
Si ottiene:
sx(0.714)= 30.5x0.714=21.8 m
Corso di Fisica AA 2011-2012
Cap.3
Esempio 4. Gittata di un proiettile (o Salto in lungo)
Consideriamo un proiettile lanciato da terra con velocità
iniziale v0. Sia θ l’inclinazione della velocità. Le componenti
orizzontale e verticale della velocità iniziale sono quindi:
v 0 x | v | cosθ
v0= = 0
v 0 y | v 0 | senθ
ed inoltre:
v0 xt
s(t)= 1 2
− 2 gt + v0 y t
La gittata R del proiettile è la distanza sx percorsa quando la quota sy è zero:
sy(t)= - ½ gt2+ v0yt=0
Risolvendo otteniamo t=0 (istante in cui si lancia il proiettile) e -½ gt+ v0y=0 cioè
t= 2v0y/g
Questo è il tempo di volo del proiettile. La gittata R è il valore di sx(t)= v0xt all'istante t= 2v0y/g:
R=2v0xv0y/g
cioè
R=2|v0|2cosθ senθ/g
Fissato il modulo della velocità iniziale, la gittata è massima per θ=45°. Per la simmetria delle
funzioni seno e coseno, abbiamo che cosθ senθ= cos(90°-θ)sen(90°-θ). Per cui se si calcia una palla
con un angolo di 30° o di 60°, questa cadrà alla stessa distanza, anche se traiettorie e tempi di volo
saranno differenti (lo stesso vale per le coppie di angoli di 10° e 80°, 20° e 70°, 40° e 50° ecc).
Questo è vero se il proiettile è lanciato da terra. Se è lanciato da una certa altezza dal suolo, l'angolo
corrispondente alla gittata massima non è 45°: in questo caso un tiro "teso" permette alla palla di
raggiungere una gittata maggiore (vedi figura a destra).
Quiz
Una saltatrice in lungo ha ottenuto la misura di 6 metri e 54 cm. Ammesso che abbia spiccato il
salto con un angolo di 45°, a che velocità si muoveva nel momento del salto?
Quiz
Vi trovate su una slitta trainata da cani che si muove alla velocità costante di 2 m/s e lanciate una
palla di neve in verticale alla velocità di 12 m/s. Dove andrà a cadere la palla? Dove vi troverete
rispetto alla palla nel momento in cui questa tocca terra?
Corso di Fisica AA 2011-2012
Cap.3
Esempio 5. Traiettoria di un proiettile
Qual è la traiettoria di un corpo lanciato in aria?
v0 x
Se il corpo è lanciato da terra, con velocità iniziale v0= , e facciamo coincidere l’origine degli
v 0 y
v0 xt
assi con il punto di lancio (s0x=s0y=0), la legge oraria è s(t)= 1 2
− 2 gt + v0 y t
Abbiamo quindi che il corpo si troverà ad ogni istante di tempo t nel punto P(x,y) di coordinate
x = v0 xt
2
1
y = − 2 gt + v0 y t
da cui t=x/v0x e
2
x
x
y = − g
+ v0 y
v0 x
v0 x
v
g
y = − 12 2 x 2 + 0 y x
v0 x
v0 x
1
2
Questa è l’equazione della parabola y=ax2+bx con
a = − 12
g
v0 x
2
; b=
v0 y
v0 x
dal momento che a<0, la parabola ha la concavità verso il basso, ∩
Quiz
1) che forma assume la traiettoria in assenza di gravità? (g=0)
2) che forma assume la traiettoria se il corpo è lanciato orizzontalmente? (v0y=0)
3) che forma assume la traiettoria se il corpo è lanciato verticalmente? (v0x=0)
4) come si modifica l’equazione della parabola se il corpo viene lanciato da una certa altezza h?
Corso di Fisica AA 2011-2012
Cap.3
Moto curvilineo nel piano: moto circolare uniforme
E' il moto di un punto P su di una circonferenza che ruota con velocità in modulo costante.
Sia ϑ l'angolo in radianti descritto dal raggio R durante il moto di P. Lo spazio percorso sulla
circonferenza è ∆l =R∆ϑ. Il modulo della velocità è allora: |v|=∆l /∆t = R ∆ϑ /∆t.
E' utile definire la velocità angolare ω:
∆θ
ω=
∆t
Poiché l'angolo ϑ si misura in radianti, la velocità angolare ω è espressa in [rad][s]-1. Si ha quindi:
|v|=Rω
Si può dimostrare che l'accelerazione del moto circolare uniforme è un vettore perpendicolare alla
velocità, diretto verso il centro, e di modulo
|a|=|v|2/R
o, poiché |v|=Rω
|a|=Rω2
Questa accelerazione è detta centripeda perché rivolta verso il centro della circonferenza.
Esempio 1 (continua). Consideriamo di nuovo il ciclista dell’esempio 1. Qual è la sua
accelerazione? Qual è la velocità angolare?
Il moto è circolare uniforme perché la velocità istantanea v è costante in modulo. Quindi a è un
vettore diretto verso il centro della circonferenza e di modulo:
|a|=|v|2/R =13.092/1000=0,171 m/s2
Dalla relazione tra velocità e velocità angolare abbiamo poi:
ω= |v|/R=13.09/1000=0,01309 rad/s
Corso di Fisica AA 2011-2012
Cap.3
Esercizio. Dovete acquistare una centrifuga scegliendo tra due modelli: il tipo A ha 20 cm di
diametro e velocità di rotazione di 1000 giri al minuto; il tipo B ha diametro=18 cm e velocità di
rotazione=1200 giri/minuto. Volendo scegliere quella che assicura la maggior accelerazione, quale
scegliereste?
Il modulo dell’accelerazione è: |a|= Rω2
Per la centrifuga A abbiamo: R=0.1 m;
ω=1000 [giri][min]-1
1 [min]=60 [s]; 1 [giro]=2π [rad]
ω=2π1000/60 [rad] [s]-1=104,7 rad/s
|a|= 0.1x104,72=1096.5 [m][s]-2
Per la centrifuga B abbiamo: R=0.09 m;
ω=2π1200/60 [rad] [s]-1=125,7
|a|= 0.09x125,72=1421 [m][s]-2
Pertanto acquisterete la centrifuga B
Quiz
Le pale di un ventilatore da soffitto si muovono a 12 giri/min. Una mosca, posatasi su una pala
vicino al perno centrale, cammina verso l’esterno della pala. La mosca non riesce a rimanere sulla
pala se il vento soffia a più di 2 m/s. Fino a che distanza dal centro riuscirà a muoversi prima di
perdere l’appiglio?
Moto circolare accelerato
E’ il moto di un punto su di una circonferenza che ruota con velocità in modulo variabile. In questo
caso la velocità è un vettore v(t) ancora diretto nella direzione della tangente alla circonferenza.
L’accelerazione invece non sarà più un vettore diretto verso il centro della circonferenza. Potremo
però scomporre a(t) in due componenti perpendicolari: uno diretto verso il centro e l’altro nella
direzione della tangente. Queste sono rispettivamente le componenti centripeta, aN, e tangente, aT,
dell’accelerazione. Si veda il grafico:
aT=∆|v|/ ∆t
a
aN=Rω2
Corso di Fisica AA 2011-2012
Cap.3
Applicazione di Biomeccanica: stimolazione dell’utricolo del labirinto.
Il labirinto è l’organo dell’equilibrio, posto nell’orecchio interno. Ne abbiamo due, distanziati di
circa 7 cm. Il labirinto comprende una struttura orizzontale (utricolo) ed una verticale (sacculo) che
ci permettono di valutare la posizione della testa, e canali semicircolari per valutare i movimenti
della testa.
Litografia dell’orecchio interno tratta da Gray's Anatomy of the Human Body (1918);
l’utricolo si trova all’interno del vestibolo.
Queste strutture contengono una massa gelatinosa appesantita da particelle (otoliti) che si muovono
in risposta alle variazioni di direzione della gravità (dovute ad un cambiamento nella posizione della
testa) ed alle accelerazioni del capo. Cellule specializzate misurano questi movimenti. In
particolare, l’utricolo (sensibile alle accelerazioni orizzontali) risponde a piegamenti del capo che
provocano accelerazioni superiori a 0.006g.
Per stimolare gli utricoli, il paziente seduto su una sedia rotante è fatto ruotare a velocità costante.
In questo modo i due utricoli sono stimolati da accelerazioni in modulo uguale ma opposte. Per
stimolare un solo utricolo alla volta, durante la rotazione il paziente viene spostato di 3,5 cm lungo
l’asse definito dai labirinti. In questo modo gli utricoli si trovano uno sull’asse di rotazione, l’altro a
7 cm da esso.
Corso di Fisica AA 2011-2012
Cap.3
L’accelerazione centripeda subita dagli utricoli è |a|=Rω2 con R=0 per l’utricolo sull’asse di
rotazione, R=0.07 [m] per quello fuori asse.
Perché questa accelerazione superi la soglia è necessario che |a|=0.07ω2 sia maggiore di
0.006g=0.0588 [m][s]-2 cioè
0.07ω2>0.0588
ω2>0.0588/0.07
e quindi: ω>0.917 [rad][s]-1
Poiché 2π[rad]=360°
1 [rad]= 360°/2π==57,3°
Quindi ω=0.917 [rad][s]-1e corrisponde a circa 53° s-1
Inoltre poiché 2π[rad]=1 [giri]
1 [rad]= 1/2π [giri]
1 [s]-1= 60 [min] -1
ω=0.917 [rad][s]-1e corrisponde a 8,75 giri/min.












