Corso di Eccellenza - Geometria
II Anno del Corso di Laurea in Matematica
10, 17, 24 e 31 marzo 2009
“Tutto quello che avreste voluto sapere su S2
e non avete mai osato chiedere (o quasi)”
Andrea Sambusetti
Contenuti di massima
I. Curve speciali sulla sfera
(Lunghezze, distanza, geodetiche e lossodromiche)
II. Aree
(Calotte, biangoli e triangoli, eccesso angolare)
III. Trigonometria sferica.
IV. Carte geografiche e loro proprietà
(Inversioni, proiezione sterografica, proiezioni cilindriche)
V. Magie del gruppo delle isometrie di S2
(Regola del parallelogramma sferico, quaternioni, briciole di S3 )
VI. Il pallone da football ed altre stranezze (forse)
(....e niente curvatura?)
1
I. Curve speciali sulla sfera.
Problemino I.1 Siano p, q ∈ E2 . Dimostrare che la curva più corta che
unisce p a q è il segmento pq (parametrizzato in modo opportuno).
Indicazioni:
– Scrivere una curva γ da p a q in coordinate polari di centro P .
√
– Cosa rappresentano geometricamente i due addendi nella formula |γ 0 | = r02 + r2 ϑ02 ?
(Questa strada non è l’unica possibile, ma è utile per l’esercizio seguente).
Problema I.2 (Geodetiche)
(i) Siano p, q ∈ S2 : dimostrare (senza l’uso del calcolo differenziale) che la
curva più corta su S2 che unisce p a q è un arco di cerchio massimo.
(ii) Dimostrare la stessa cosa con l’uso di derivate e integrali.
Nota: i cerchi massimi di S2 , parametrizzati da lunghezza d’arco, sono detti le geodetiche (o segmenti geodetici) della sfera. Si noti che una geodetica minimizza la distanza
tra i suoi estremi se e solo se la sua lunghezza è al massimo la metà di un cerchio massimo
(perché?); in tal caso, si parla di geodetica minimizzante.
Indicazioni per (i):
Ricordare che la lunghezza di una curva è definita come `(γ) = supPγ `(Pγ ), dove Pγ è
una poligonale approssimante per γ.
Indicazioni per (ii): mettere P nel polo nord, e spezzare il vettore γ 0 in una componente
radiale (tangente ai meridiani) ed una ortogonale (tangente ai paralleli); adaattare quindi
l’argomento di I.1.
Problemino I.3
(i) Determinare le curve del piano che formano angolo costante con i raggi
uscenti dall’origine.
(ii) Sia γ una tale curva, diversa da una circonferenza o un raggio. Si consideri
la parte di γ contenuta nel disco unitario di centro l’origine. Quanti giri fa
γ attorno all’origine? Quindi quant’è la sua lunghezza? (Zenone insegna).
Indicazione: usare coordinate polari nel piano.
Problema I.4 (Lossodromiche)
Una curva su S2 che fa angolo costante con i meridiani è detta lossodromica.
(i) Qual è l’interesse pratico?
(ii) Determinare una parametrizzazione delle lossodromiche, e descriverne
qualitativamente l’andamento.
(iii) C’è relazione con le curve del Problema I.3?
Indicazioni:
– Scrivere una tale curva γ(t) in coordinate sferiche (λ, ϕ) (dove λ è l’angolo di longitudine,
e ϕ l’angolo di latitudine, entrambi pensati come variabili in R), e trovare la relazione che
sussiste tra λ(t) e ϕ(t) (risolvendo un’equazione differenziale)
– Per (iii), confrontare col Problema III.9.
2
II. Aree.
Richiami: cos’è lo spazio tangente.
– Dato un sottoinsieme S ⊂ E3 , un vettore unitario u si dice tangente
ad S in s se esiste
−
−
→
ss
n
una successione di punti sn ∈ S tali che: sn → s e u = limn→∞ kss
.
−
−
→k
n
– Lo spazio tangente ad S in un suo punto s è l’insieme (unione di rette per l’origine)
Ts S = {λu ∈ E3 | u versore tangente ad S in s, λ ∈ R}
Richiami: sulle applicazioni differenziabili f : U ⊂ E2 → S2 .
– Una parametrizzazione (di una porzione) di S2 è una funzione f : U ⊂ E2 → S2 .
– Una parametrizzazione f : U → S2 si dice regolare in p = (x, y) se i vettori {fx (p), fy (p)}
sono linearmente indipendenti.
– Una carta di S2 è una parametrizzazione regolare e iniettiva f : U → S2 .
– Il differenziale di una parametrizzazione f : U → S2 in p = (x, y) è l’applicazione lineare
(df )p : E2 → E3 definita da (df )p (x1 , x2 ) := fx (p)x1 + fy (p)x2
Problemino II.1 (Spazio tangente ad S2 )
Sia f : U → S2 una parametrizzazione regolare con f (p) = s ∈ S2 :
(i) mostrare che Ts S2 = {u | u · s = 0};
(ii) mostrare Im(df )p ⊂ Ts S2 , dunque (df )p : E2 → Ts S2 ;
(iii) mostrare che se f è regolare in p allora Ts S2 = Span(fx (p), fy (p))
(pertanto in tal caso (df )p è un isomorfismo E2 ∼
= Ts S2 ).
Osservazioni:
– In generale, se S è una superficie differenziabile (come per es. S2 ), lo spazio tangente
Ts S è un piano vettoriale di E3 , e si ha sempre Ts S = Span(fx (p), fy (p)), per la scelta di
una qualsiasi carta f : U → S di S intorno ad s = f (p).
– Quando f : U → S2 è una carta, si considera a volte l’inversa f −1 : f (U ) ⊂ S2 → U ,
il cui differenziale è (per definizione) l’applicazione inversa (df −1 )s := (df )−1
p .
Richiami: area.
R
Se f : U ⊂ E2 → S2 è una carta, l’area di V = f (U ) è definita da A(V ) = U kfx ∧fy kdxdy.
– Perché? (Confrontare con il Problema II.4)
– Il valore A(V ) non dipende dalla particolare carta f scelta per parametrizzare V : perché?
Problemino II.2 (Area di S2 in diverse coordinate)
(i) Descrivere almeno 5 carte sostanzialmente differenti per S2 .
(ii) Utilizzarle per calcolare A(S2 ) in altrettanti modi differenti.
Problema II.3 (Archimede ci dà una pista)
(i) Si tagli la sfera con piani paralleli a distanza ∆n = n1 tra loro, e si inscriva
in ogni calotta sferica di spessore ∆n cosı̀ ottenuta un tronco di cono di ugual
basi. Calcolare la somma An delle aree di questi tronchi di cono, e verificare
che Archimede aveva visto giusto: A(S2 ) = limn→∞ An .
(ii) Sia C(h, ∆) = S2 ∩ {h − ∆2 ≤ z ≤ h + ∆2 } la calotta sferica di spessore ∆
tagliata ad altezza h. Descrivere come varia A(C(h, ∆)) in funzione di h.
3
Problema II.4 (Lampione di Schwarz)
Consideriamo il cilindro circolare retto C, di asse z e raggio unitario, compreso tra i piani z = 0 e z = 1. Tagliamo C in N fette orizzontali di eguale
altezza 1/N , ognuna delle quali avente per base un cerchio Ck . Inscriviamo nella base C2k−1 di ogni fetta “dispari” un poligono regolare ad n lati;
analogamente inscriviamo nella sua faccia superiore (la base della fetta pari
C2k ) lo stesso poligono regolare, ma con vertici sfasati di π/n. Infine uniamo,
in ogni fetta, ogni vertice del poligono inscritto sulla faccia inferiore con i due
vertici più vicini del poligono inscritto sulla faccia superiore.
Si ottiene in tal modo un poliedro Pn,N , unione di 2nN triangoli Ti , inscritto
nel cilindro C, detto lampione di Schwarz.
(i) Si verifichi che, se n → ∞ e N → ∞, il diametro di ogni triangolo Ti e la
distanza del poliedro Pn,N dal cilindro tendono entrambi a zero.
(ii) Si mostri che, ponendo N = n, si ottiene limn→∞ A(Pn,n ) = 2π = A(C).
(iii) Tuttavia, si mostri che variando la relazione tra n ed N , si può ottenere
limn,N →∞ A(Pn,N ) 6= 2π e addirittura limn,N →∞ A(Pn,N ) = +∞ (!).
Osservazione: cosa non funziona, in (iii), che invece non succede nell’approssimazione
di Archimede?
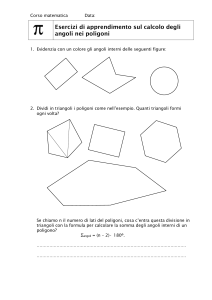
Problema II.5 (Area di un triangolo sferico)
Ì è un sottoinsieme di S2 delimitato da tre segmenti
Un triangolo sferico ABC
¯ BC,
¯ CA
¯ (il triangolo si dice degenere
geodetici minimizzanti consecutivi AB,
se i segmenti giacciono su una stessa geodetica).
Î (o lunula) è un sottoinsieme di S2 delimitato da
Un biangolo sferico AB
¯ BA
¯ (il biangolo si dice degenere se i
due segmenti geodetici consecutivi AB,
segmenti giacciono su una stessa geodetica).
Dare un esempio di biangolo sferico non degenere (notare che non esistono
“biangoli” non degeneri nel piano euclideo!): quanto valgono gli angoli ai
vertici A, B?
(i) Calcolare l’area dei biangoli sferici.
Ì con angoli ai vertici α, β, γ.
(ii) Sia assegnato un triangolo sferico ABC
Scomporre la sfera in unione (non disgiunta) di biangoli, quindi dedurre che
Ì =α+β+γ−π
A(ABC)
(iii) Esistono triangoli “simili” (ma non congruenti) in geometria sferica? (cf.
Problema V.2)
Osservazioni:
– Paragonare con il caso euclideo; qual è la prima differenza qualitativa?
– Confrontare questa geometria con i postulati euclidei.
– Ritrovare la formula dell’area di un triangolo sferico usando il Teorema di Gauss-Bonnet
per una superficie S, con bordo C 1 a tratti ∂S, e vertici Vi :
Z
Z
X
K+
κ+
i = 2πχ(S)
S
∂S
Vi
dove K è la curvatura gaussiana della superficie, κ la curvatura geodetica del bordo, ed i
gli angoli esterni ai vertici.
4
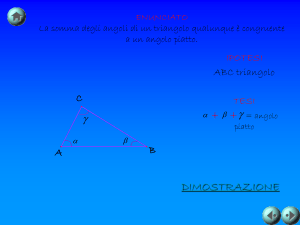
III. Trigonometria Sferica
Problema III.1 (Teorema del Coseno e Teorema di Pitagora sferici)
Ì con angoli ai vertici
Consideriamo un triangolo sferico non degenere ABC
α, β, γ e lati (opposti rispettivamente ai vertici A, B, C) di lunghezza a, b, c.
Ì in C: scomporli nelle
(i) Siano ~a, ~b i vettori unitari tangenti ai lati di ABC
−→ −−→ −→
loro componenti rispetto alla base OA, OB, OC;
(ii) calcolare cos γ e dedurre il Teorema del Coseno sferico:
cos c = cos a cos b + sin a sin b cos γ
(iii) Dedurre il Teorema di Pitagora per triangoli rettangoli sferici.
Osservazione: questo è l’analogo del Teorema del Coseno euclideo, che esprime il lato c
di un triangolo in funzione degli altri due a, b e dell’angolo γ tra essi: c2 = a2 +b2 −2ab cos γ.
Problemino III.2 (Teoremi dei Cateti e Teorema dei Seni)
Ì con angoli ai vertici α, β
Consideriamo un triangolo rettangolo sferico ABC
π
e γ = 2 , e lati opposti a, b, c. Dimostrare gli analoghi dei Teoremi dei Cateti:
(i) (Teorema del Cateto tramite angolo adiacente) tan a = tan c cos β
(ii) (Teorema del Cateto tramite angolo opposto) sin a = sin c sin α
Indicazione: utilizzare i Teoremi del Coseno e di Pitagora appena dimostrati.
Problemino III.3 (Teorema dei Seni)
Ì con angoli ai vertici
Consideriamo un triangolo rettangolo non degenere ABC
α, β e γ e lati opposti a, b, c. Dimostrare l’analogo del Teorema dei Seni:
sin b
sin c
sin a
=
=
sin α
sin β
sin γ
Problema III.4 (La geometria piana come limite di quella sferica)
Considerare dei triangoli sferici con angoli fissati e i cui lati a, b, c → 0.
Sviluppare le formule appena trovate al primo ordine siginificativo.
Cosa si ottiene? Qual è il significato geometrico di quanto trovato?
Nota: tutti i teoremi appena enunciati su S2 hanno analoghi in H2 , che si ottengono
sostituendo le funzioni trigonometriche in a, b, c con le corrispettive iperboliche!
Problemino III.5 (What’s good for?)
Considerate le coordinate geografiche delle città sotto riportate, calcolare:
(i) la distanza in linea d’aria tra Buenos Aires e Atene;
(ii) in che direzione è la Mecca da Jakarta;
(iii) la rotta di un areo che parte da Cape Town verso Pechino.
Nota: le direzioni e le rotte geografiche si danno sempre in gradi da Nord, in senso
orario rispetto alla normale uscente dalla sfera terreste
5
Coordinate geografiche:
Atene
Cape Town
Buenos Aires
Jakarta
Mecca
Pechino
ϕ
38◦ N
33◦ 560 S
34◦ 400 S
6◦ 080 S
21◦ 260 N
39◦ 550 S
λ
23◦ 440 E
18◦ 280 E
58◦ 300 W
106◦ 450 E
39◦ 490 E
116◦ 260 E
Problema III.6 (Dualità polare)
Sia a un arco orientato di geodetica di S2 ; il punto polare di a è il punto
−−→
A∗ ∈ S2 tale che il vettore OA∗ è ortogonale al piano su cui giace a, e
rispetto al quale a è percorso in senso antiorario.
Ì un triangolo sferico con angoli ai vertici α, β, γ e lati
Sia ora T = ABC
opposti a, b, c. Si scelga un verso di percorrenza del bordo abc del triangolo.
∗ B ∗ C ∗ è il triangolo che ha per vertici i punti polari
Il triangolo polare T ∗ = A
A∗ , B ∗ , C ∗ di a, b, c, angoli ai vertici α∗ , β ∗ , γ ∗ e lati opposti a∗ , b∗ , c∗ .
Mostrare che:
(i) (T ∗ )∗ = T ;
(ii) a∗ = π − α, b∗ = π − β, c∗ = π − γ;
(iii) α∗ = π − a, β ∗ = π − b, γ ∗ = π − c.
Da ciò segue che per ogni formula trigonometrica sferica vale una formula
duale ottenuta scambiando i valori dei lati con i supplementari dei valori degli
angoli (e viceversa); per es., la formula duale del teorema del coseno per un
Ì con angoli ai vertici α, β, γ e lati a, b, c è
triangolo sferico ABC
cos γ = sin α sin β cos c − cos α cos β
−−→ −−→
Indicazione: verificare che OA∗ , OB ∗ = a, b.
IV. Carte geografiche e loro proprietà.
Problema IV.1 (Carte globali per S2 ?)
(i) Esiste una parametrizzazione regolare suriettiva f : U → S2 di un aperto
del piano in S2 ?
(ii) Esiste una parametrizzazione regolare iniettiva e suriettiva (cioè una carta
“globale”) f : U → S2 da un aperto del piano in S2 ?
(In ogni caso, portare un esempio o giustificare la risposta negativa).
Richiami: cosa significa che una trasformazione “conserva le geodetiche”?
Una carta di S2 (o un diffeomorfismo tra aperti di En ) conserva le geodetiche se l’immagine
di ogni geodetica è una geodetica. Le carte di S2 che conservano le geodetiche sono note,
in cartografia, col nome di carte gnomoniche.
Problema IV.2 (Carta gnomonica)
Esibire una carta di S2 che conserva le geodetiche.
6
Richiami: cosa significa che una trasformazione “conserva le aree”?
Una carta f di S2 (o un diffeomorfismo tra aperti di En ) conserva le aree se A(f (S)) =
A(S) per ogni insieme (misurabile) S. Una carta di S2 che preserva le aree si dice, in
cartografia, una carta equivalente.
Problemino IV.3 (Jacobiano)
Un diffeomorfismo f : U → V tra aperti di En conserva le aree se
Jacp (f ) := |det(df )p | = 1 per ogni p ∈ U , per la nota formula del cambio di
variabili
Z
Z
g(q)dq = Jacp (f )g(f (p))dp
U
V
2
Mostrare che una carta f : U → S conserva le aree se il suo Jacobiano
Jacp (f ) := |det[(df )p ]B
B 0 | = 1 ∀p
dove [(df )p ]E
B indica la matrice (2 × 2) del differenziale (df )p rispetto a due
qualsiasi basi ortonormali B, B 0 rispettivamente di E2 e Tf (p) S2 .
Richiami: cosa significa che una trasformazione “conserva gli angoli”?
– Se α, β : I → En sono due curve (differenziabili e regolari) con p = α(t) = β(t),
l’angolo tra α e β in p (più precisamente: in t) è l’angolo formato dai loro vettori tangenti
α0 (t), β 0 (t) (denotato p α, β oppure t α, β)
– Una carta f di S2 (o un diffeomorfismo tra aperti di En ) conserva gli angoli in p se
conserva gli angoli tra tutte le curve regolari passanti per p, cioè
f (P ) f ◦ α, f ◦ β = P α, β
(Per una carta f : U → S ciò equivale a chiedere che la sua inversa f −1 conserva gli angoli
in s = f (p) tra tutte le curve che giacciono su S2 , passanti per s).
– Per la formula della derivata di una funzione composta, dire che una carta (o un diffeomorfismo) f conserva gli angoli in p è equivalente a dire che (df )p conserva gli angoli.
Un diffeomorfismo o una carta che conserva gli angoli in ogni punto si dice una trasformazione conforme.
2
Problemino IV.4 (Trasformazioni conformi lineari e affini)
Sia f : En → E0n un’applicazione lineare tra spazi euclidei. Mostrare che le
seguenti sono condizioni equivalenti:
(a) f conserva gli angoli
(b) esiste λ > 0 tale che kf (u)k2 = λ2 kuk2 per ogni u ∈ En
(c) esiste λ > 0 tale che f (u) · f (v) = λu · v per ogni u, v ∈ En
(d) in coordinate cartesiane su En e E0n , si ha f (X) = λAX, con λ 6= 0, A ∈ O(n)
Una tale trasformazione si dice una similitudine lineare.
Osservazioni:
– Pertanto, una carta f : U → S2 (o un diffeomorfismo tra aperti di En ) conserva gli angoli
in p se e solo se il suo differenziale (df )p è una similitudine lineare.
– In particolare, una trasformazione affine f : En → En conserva gli angoli se e solo se
f (X) = λAX + b, con λ 6= 0, A ∈ O(n), b ∈ En . Una tale trasformazione si dice una
similitudine.
7
Problema IV.5 (Trasformazioni conformi non affini)
L’ inversione di centro c e raggio r è l’applicazione ic,r : En \ {c} → En \ {c}
che manda un punto p nel punto ic,r (p) che giace sullo stesso raggio uscente
−−−−→
−
da c e contenente p, e tale che k→
cpk · kc ic,r (p)k = r2 .
(i) Esplicitare ic,r (x1 , x2 , x3 ) e mostrare che ic,r è un diffeomorfismo.
(ii) Mostrare che ic,r è conforme.
(iii) Esibire almeno un altro esempio (sostanzialmente differente) di trasformazione conforme di E2 che non sia né una similitudine né un’inversione
(né una loro composizione!)
Osservazioni:
– Paragonare con il caso dei diffeomorfismi f : En → En che conservano le distanze: ne
esistono che non siano affini?
– Le inversione hanno la proprietà di conservare la famiglia costituita dalle rette e dai
cerchi. Sapreste dimostrarlo? Quali sono le rette che vengono trasformati in cerchi?
– L’inversione è una trasformazione fondamentale, a causa del Teorema di Liouville:
ogni diffeomorfismo conforme tra aperti di En (per n > 2) è una similitudine
oppure è la composizione di un’inversione con una similitudine.
Da ciò segue che l’insieme di tutte le trasformazioni conformi di Sn = En ∪ {∞}
(per n > 2) è il gruppo:
GM (n) = {f : Sn → Sn | f (X) = λAj(X), λ ∈ R+ , A ∈ O(n), j = id oppure j = io,1 }
che è detto gruppo di Moebius.
Definizioni: linee standard, linee/insiemi di isometria e di equivalenza di una carta.
Sia f : U → S2 una carta:
– una curva γ di U si dice una linea standard se le lunghezze misurate lungo f ◦ γ sono le
stesse delle lunghezze misurate lungo γ;
– l’insieme dei punti p in cui (df )p è un’isometria si dice l’insieme (o le linee) di isometria;
– l’insieme dei punti p in cui Jacp f = 1 si dice l’insieme (o le linee) di equivalenza.
Problemino IV.6 (“Carta di Eratostene”)
Longitudine e latitudine (λ, ϕ) corrispondono alla carta E : U → S2 detta di
Eratostene:
(i) La carta E conserva le geodetiche? È equivalente? È conforme?
(ii) Trovare le linee standard, di equivalenza e di isometria.
8
Problemino IV.7 (Carta di Mercatore)
La carta di Mercatore è ottenuta da quella di Eratostene eseguendo una
riparametrizzazione (crescente, non lineare) y = y(φ) dell’asse φ, in modo
che gli angoli vengano conservati:
(i) Descrivere esplicitamente la carta di Mercatore M : U → S2 ;
(ii) mostrare che M manda lossodromiche in rette;
(iii) trovare le linee standard, di equivalenza e di isometria.
Osservazione: le proprietà (ii) e la conformità fanno della carta di Mercatore la carta
più utile nella navigazione e nel carteggio, in quanto le rotte corrispondono a delle linee
rette nella carta, e gli angoli possono essere misurati sulla carta senza errori.
Problemino IV.8 (Carta di Lambert, o di Archimede)
La carta di Lambert è ottenuta da quella di Eratostene eseguendo una riparametrizzazione (crescente, non lineare) z = z(φ) dell’asse φ, in modo che
le aree vengano conservate:
(i) Descrivere esplicitamente la carta di Lambert L : U → S2 ;
(ii) trovare le linee standard e di isometria.
Osservazioni: tale carta è ottenuta proiettando ogni punto p di S2 sul cilindro C a
lei tangente lungo l’equatore, nella direzione della retta per p ortogonale all’asse N S, e
quindi, sviluppando il cilindro sul piano: essa corrisponde cioè a prendere su S2 coordinate
cilindriche (longitudine e altezza λ, z).
– Dare una dimostrazione elementare del fatto che L preserva le aree (senza differenziale).
– La proprietà di equivalenza fa della carta di Lambert una carta adatta a studi geograficostatistici. Di seguito le immagini di ulteriori simili proiezioni cilindriche, allo scopo di
ottenere carte con linee standard/d’isometria che tagliano particolari regioni del globo
(i.e. l’Europa):
9
Problema IV.9 (Proiezione stereografica)
La proiezione stereografica (standard) è la carta πN : E2 → S2 ottenuta
proiettando ogni punto p del piano z = 0 sulla sfera, nella direzione della
retta congiungente p con il polo nord N (variando N e il piano di proiezione,
si ottengono tutte le carte geografiche comunemente dette “stereografiche”).
(i) Verificare che πN conserva gli angoli;
(ii) verificare che πN trasforma le geodetiche di S2 in segmenti o archi di
cerchio del piano;
(iii) trovare le linee standard, di equivalenza e di isometria.
(iv) C’e’ qualche relazione con l’inversione studiata in III.5?
Problema IV.10 (La ricerca di una carta “perfetta”)
(i) È possibile trovare una carta di S2 che conserva geodetiche e angoli?
(ii) È possibile trovare una carta di S2 che conserva angoli e aree?
(iii) È possibile trovare una carta di S2 che conserva aree e geodetiche?
(iv) È possibile trovare una carta di S2 che conserva le distanze?
Osservazione: la curvatura di una superficie S è una funzione K(p) su S che è un
invariante di isometria; cioè, se f : S → S 0 è un’applicazione tra superfici che conserva
le distanze, allora S ed S 0 hanno ugual curvatura in punti corrispondenti (i.e. K(f (p) =
K(p). Com’è naturale, la curvatura del piano è nulla, mentre e quella di una sfera di
raggio r è uguale a 1/r2 ; da ciò segue facilmente che la risposta a (iv) è negativa.
(Ciononostante, non è necessario ricorrere alla nozione di curvatura per rispondere a (iv)).
V. Magie del gruppo delle isometrie di S2 .
Richiami: cos’è un’isometria.
– La sfera è uno spazio metrico: è dotata cioè di una funzione distanza d : S2 × S2 → R
d(A, B) = inf{`(γ) | γ curva da A a B}
che soddisfa le proprietà:
d(A, B) ≥ 0 ∀A, B
e
d(A, B) = 0 ⇔ A = B
d(A, B) = d(B, A) ∀A, B
d(A, C) ≤ d(A, B) + d(B, C) ∀A, B, C
– Un’isometria di uno spazio metrico (X, d) è un’applicazione f : X → X tale che
d(f (A), f (B)) = d(A, B) ∀A, B ∈ X
– Si noti che un’isometria di uno spazio metrico è sempre iniettiva.
– Un’isometria f : X → X di uno spazio metrico può non essere suriettiva?
10
Problema V.1 (Il gruppo delle isometrie di S2 )
(i) Mostrare che ogni isometria f : E3 → E3 è un’applicazione affine
f (X) = AX + b, dove A ∈ O(3).
(ii) Mostrare che ogni isometria f : S2 → S2 si estende ad un’ isometria
f : E3 → E3 .
(iii) Mostrare che il gruppo delle isometrie della sfera è Is(S2 ) ∼
= O(3).
Note:
– Le isometrie di En sono dette anche congruenze (o trasformazioni rigide); per(iii), il
gruppo delle isometrie di S2 coincide con il sottogruppo delle congruenze lineari di En .
– Due sottoinsiemi S, S 0 di En sono detti congruenti se esiste una congruenza f : En → En
tale che f (S) = S 0 .
– Notare che se due sottoinsiemi S, S 0 ⊂ S2 sono congruenti, allora esiste una congruenza
lineare (cioè che conserva S2 ) tale che f (S) = S 0 (perché?)
Problema V.2 (Tripla omogeneità di S2 )
(i) Mostrare che triangoli sferici con lati uguali sono congruenti;
(ii) Mostrare che triangoli sferici con angoli uguali sono congruenti.
La proprietà (i) si enuncia anche dicendo che Is(S2 ) agisce transitivamente
su terne di punti a ugual distanza.
Problema V.3 (“Regola del parallelogramma” su S2 )
Siano R~a,α , R~b,β due rotazioni di assi orientati ~a e ~b ed angoli α, β ∈ (0, π).
La composizione R = R~b,β ◦ R~a,α è ancora una rotazione: sapreste calcolarne
l’asse e l’angolo? Questo esercizio vi insegna come fare, geometricamente.
Siano A, B i cerchi massimi orientati lasciati invariati rispettivamente dalle
rotazioni R~a,α e R~b,β , e sia o ∈ A ∩ B. Si consideri quindi il triangolo sferico
∆ = { o , A = R~a−1
, α (o) , B = R~b, β (o) }
2
2
¯
e chiamiamo C la geodetica su cui giace il lato AB.
Siano infine ∆− , ∆+ i triangoli sferici simmetrici di ∆ rispetto ai vertici A, B.
(i) Dimostrare che R(∆− ) = ∆+ ;
¯
(ii) dedurre che R è la rotazione di cerchio invariante C ed angolo 2AB.
Provare con questo metodo per esempio a calcolare:
• angolo e asse della composizione di due rotazioni di angolo π rispetto
a due assi ortogonali (p.es. ~a = √12 (1, 0, 1), ~b = √13 (1, 1, −1)).
• angolo e asse della composizione di due rotazioni di angolo π rispetto
a due assi ~a, ~b che formano tra loro angolo γ̃ (p.es. ~a = √12 (1, 0, 1),~b =
√
1
(
4
√ √
2, 2 3, 2)).
• l’angolo di rotazione della composizione di due rotazioni di π4 rispetto
√
a due assi ~a, ~b che formano tra loro angolo γ̃ t.c. cos γ̃ = 1 − 2.
Nota: per apprezzare la semplicità di questa formula, è importante (almeno una volta
nella vita) provare a comporre due rotazioni qualsiasi esprimendole come matrici, moltiplicandole tra loro, quindi trovando l’autospazio della matrice risultante e il nuovo angolo
di rotazione).
11
Problemino V.4 (Quaternioni di Hamilton)
Siano i, j, k tre simboli. Lo spazio dei quaternioni è l’insieme
H = {t + xi + yj + zk | t, x, y, z ∈ R}
dove t + xi + yj + zk è una semplice espressione formale. Su questo spazio si
definiscono le seguenti operazioni:
Moltiplicazione per un numero reale :
λ(t + xi + yj + zk) = λt + λxi + λyj + λzk
Somma + :
(t + xi + yj + zk)+(t0 + x0 i + y 0 j + z 0 k) = (t + t0 ) + (x + x0 )i + (y + y 0 )j + (z + z 0 )k
Prodotto · :
– si definiscono prima i prodotti
i2 = i · i = −1
j2 = j · j = −1
k2 = k · k = −1
i·j=k
j·k=i
k·i=j
– quindi si impone che · sia distributiva rispetto a +, e si riarrangiano i
termini nel giusto ordine. Per es.:
(2 + 3j − k) · (i + 2k) = 2i + 4k + 3j · i + 6j · k − k · i − 2k2 = 2i + 4k − 3k + 6i − j + 2 = 2 + 8i − j + k
Prodotto scalare ≺ ·, · :
≺ t + xi + yj + zk, t + xi + yj + zk = tt0 + xx0 + yy 0 + zz 0
Inoltre, dato q = t + xi + yj + zk ∈ H si pone:
Re[q] = t
(la parte reale di q)
V e[q] = xi + yj + zk (la parte vettoriale di q)
q̄ = t − xi − yj − zk (il coniugato di q)
√
|q| = < q, q >
(la norma di q)
Mostrare che:
(i) (H, +, ·) è un corpo (i.e. un campo non commutativo), che contiene una
copia naturale di R e C come sottocampi; per questo pensiamo a H come ad
un’ estensione di R e C.
(ii) H ha una struttura naturale di R-spazio vettoriale di dimensione 4 (con
base {1, i, j, k}) e di C-spazio vettoriale di dimensione 2 (con base {1, j}).
(iii) (H, ≺ ·.· ) è uno spazio euclideo (con base ortonormale {1, i, j, k}), e
si identifica in modo naturale con E4 ; inoltre, c’è un’identificazione naturale,
che utilizzeremo sempre nel seguito:
E3 = {xi + yj + zk | x, y, z ∈ R} ⊂ H
(che spiega la notazione usuale per i versori degli assi coordinati in E3 ).
(iv) H contiene due sottogruppi interessanti rispetto al prodotto:
K = {1, i, j, k}
H1 = {q ∈ H | |q| = 1}
(gruppo di Klein)
(gruppo dei quaternioni unitari)
Mostrare quindi che K è isomorfo al gruppo diedrale di ordine 4 (il gruppo
delle simmetrie del quadrato).
12
Ecco una lista delle proprietà fondamentali di cui godono le operazioni sopra
definite (verificarle tutte). Per ogni q, q 0 ∈ H, valgono:
(q̄) = q
q + q 0 = q + q¯0
qq 0 = qq 0
q = −q ⇔ q ∈ E3
q=q ⇔ q∈R
t ∈ R ⇒ tq = qt e tq = tq = qt
q ∈ R ⇔ q 2 ∈ R+
2
|q| =≺ q, q = qq ≥ 0
1
e
(1)
(2)
(3)
q ∈ E3 ⇔ q 2 ∈ R−
(4)
2
(5)
|q| =≺ q, q = 0 ⇔ q = 0
q 6= 0 ⇒ q −1 = q̄/|q|2 e |q −1 | = |q|−1
(6)
|qq 0 | = |q||q 0 |
(7)
Re[qq 0 ] = Re[q]Re[q 0 ] − ≺ V e[q], V e[q 0 ] (8)
V e[qq 0 ] = Re[q]V e[q 0 ] + V e[q]Re[q 0 ] + V e[q] ∧ V e[q 0 ]
(9)
Nota: Una realizzazione matriciale dei quaternioni si ottiene prendendo
ßÅ
ã
™
a b
0
H =
| a, b ∈ C
−b̄ ā
con le usuali operazioni di somma e prodotto righe per colonne. Definendo l’applicazione
R-lineare f : H → H0 sulla base {1, i, j, k} come
Å
ã
Å
ã
Å
ã
Å
ã
1 0
i 0
0 1
0 i
f (1) =
f (i) =
f (j) =
f (k) =
0 1
o −i
−1 0
i 0
si ottiene allora un isomorfismo di corpi.
Problema V.5 (Rotazioni e quaternioni)
Per ogni u ∈ H1 definiamo ρu : H → H come ρu (q) = uqu−1 .
Mostrare che:
(i) l’applicazione ρu è un automorfismo di H;
(cioè un omomorfismo biettivo del corpo H in sé)
(ii) la restrizione ρu |R è l’identità;
(iii) la restrizione ρu (E3 ) ⊂ E3 , e che ρu |E3 è una rotazione.
Scrivere ora u nella forma u = cos ϑ + sin ϑ v, con v vettore unitario di E3
(è possibile?), e scegliere una base ortonormale v1 , v2 del piano z ⊥ ⊂ E3 .
Mostrare quindi che:
(v) la rotazione ρu |E3 ha asse z;
(vi) l’angolo di rotazione di ρu |E3 rispetto all’asse orientato z è 2ϑ.
(vii) Infine, dedurre che si può definire un’applicazione ρ : H1 → SO(3), e
che questa applicazione è un omorfismo di gruppi, è suriettiva e ha kernel
uguale a ±1.
Come si possono comporre allora due rotazioni con l’uso di quaternioni?
A quali quaternioni corrispondono le rotazioni di π2 ?
Ricalcolare con questo metodo asse e angolo delle rotazioni del Problema
V.3, ottenute per composizione.
1
ma ≺ q, q 0 6= qq 0 in generale.
13
Problema V.6 (Sfera tridimensionale S3 )
La sfera (unitaria) tridimensionale S3 è l’insieme dei punti di R4 a distanza
unitaria dall’origine.
(i) (Per chi ha fatto un po’ di topologia) Mostrare che S3 si ottiene topologicamente dalla palla chiusa unitaria B(o, 1) = {P ∈ R3 | d(o, p) ≤ 1}
identificando tutti i punti del suo bordo S2 ad un unico punto: esiste cioè un
omeomorfismo B(o, 1)/∼S2 ∼
= S3 .
(ii) Verificare che S3 si identifica in modo naturale con H1 .
Questa interpretazione rispetto ad (i) ha il vantaggio di mostrare che S3 ha
una struttura naturale di gruppo, oltre che di spazio topologico.
E la sfera S1 di dimensione 1? E la sfera S2 ?
(iii) Sia SU (2) = {A ∈ GL(2, C) | A−1 = Āt } il gruppo delle matrici unitarie 2 .
Usare la descrizione matriciale dei quaternioni (cf. Nota al Problemino V.4)
per mostrare che H1 si identifica precisamente a SU (2).
(iv) L’ultimo punto del Problema V.5 ci dice inoltre che H1 /{±1} ∼
= SO(3)
(come gruppi): per questo, H1 è detto anche il gruppo Spin di SO(3). Questa
relazione si esprime anche dicendo che H1 (ovvero la sfera S3 ) è il rivestimento
universale a due fogli del gruppo delle rotazioni SO(3).
Il gruppo dei quaternioni unitari è denotato per questi motivi con vari nomi,
a seconda della struttura che si vuole sottolineare: S3 , H1 , SU (2), Spin(3).
2
queste sono precisamente le matrici che preservano la forma hermitiana standard
≺ Z, W = z1 w1 + z2 w2 di C2 (verificarlo).
14