1
CAPITOLO 2
LA TRIGONOMETRIA
I teoremi classici
La trigonometria, che vide tra i suoi padri fondatori Ipparco, Menelao e
Tolomeo, fu concepita come strumento necessario per la costruzione di
un’astronomia quantitativa, con il preciso scopo di poter prevedere il moto dei
corpi celesti, di determinare l’ora, e di compilare calendari. La
trigonometria si è rivelata uno strumento molto utile alla navigazione ed
alla geografia. Gli storici concordano nell’attribuire ad Ipparco, che visse a
Rodi e ad Alessandria e morì attorno al 125 a.C., il ruolo di fondatore
della trigonometria, e all’egiziano Claudio Tolomeo, che visse ad
Alessandria lavorando al museo e morì nel 168 d.C., il proseguimento e la
sintesi del lavoro precedentemente iniziato da Ipparco e Menelao,
riguardante la trigonometria e l’astronomia. L’opera più importante di
Tolomeo è l’Almagesto, dove in realtà si parla più di trigonometria sferica
piuttosto che di trigonometria piana, oggetto dei nostri studi.
Presentiamo una selezione di risultati e teoremi tipici della trigonometria.
Il teorema di CARNOT
In un triangolo qualsiasi valgono le seguenti relazioni:
c 2 = a 2 + b 2 − 2abcos γ
b 2 = a 2 + c 2 − 2ac cos β
a 2 = b 2 + c 2 − 2bc cos α
.
€
Dimostrazione.
Proviamo, ad esempio, la prima delle tre relazioni. Sul prolungamento del
lato AC con origine in C sia K il piede della perpendicolare al
prolungamento condotta dal vertice B. Applichiamo al triangolo rettangolo
ABK il teorema di Pitagora e le relazioni sugli angoli associati, otteniamo
2
2
(
)
2
2
così: AB = AC +CK + BK , da cui segue
(
c 2 = b + a cos π − γ
(
2
)) (
(
+ a sin π − γ
))
2
= b2 − 2abcos γ + a 2 .
Le altre due relazioni si dimostrano con considerazioni del tutto analoghe.
Un’applicazione: la formula di addizione del coseno
E’ possibile sfruttare il teorema di Carnot per dedurre la formula di addizione
del coseno
(cosγ1 cosγ 2 − sin γ1 sin γ 2 ) = cos (γ1 + γ 2 ) .
Per questo scopo scriviamo l’angolo BCˆ A come somma degli angoli BĈH e
AĈH , in simboli γ = γ1 + γ 2 . Di conseguenza
2
2
2
2
2
c 2 = AB 2 = (BH + AH )2 = BH 2 + AH
€ + 2AH ⋅ BH = a − h + b − h + 2bsin γ 2a sin γ1 .
Ora, possiamo sostituire h = a cos γ1 = bcos γ 2 , nell’espressione precedente
ed ottenere:
c 2 = a 2 + b2 − 2h ⋅ h + 2bsin γ 2a sin γ1 = a 2 + b2 − 2a cos γ1bcos γ 2 + 2bsin γ 2a sin γ1 . D’altra
parte, per il teorema di Carnot, c 2 = a 2 + b2 − 2abcos γ = a 2 + b2 − 2abcos (γ1 + γ 2 ) e,
confrontando questa espressione con quella precedentemente trovata,
risulta
(
)
(
)
− sin γ sin γ ) = cos (γ + γ ) .
2ab cos γ1 cos γ 2 − sin γ1 sin γ 2 = 2abcos γ1 + γ 2 = 2abcos γ .
Di conseguenza, (cos γ1 cos γ 2
1
2
1
Il teorema dei SENI
In un triangolo qualsiasi, dette a,b,c le misure dei lati e
opposti, sussiste la seguente relazione:
a
b
c
=
= € = 2r
sin α sin β sin γ
2
α, β , γ
,
dove r è il raggio della circonferenza circoscritta al triangolo.
Dimostrazione.
€
le ampiezze degli angoli
3
Consideriamo la figura sopra. Sia B’ il simmetrico del vertice B rispetto al
centro della circonferenza circoscritta al triangolo di partenza ABC.
Poiché l’angolo in B’ è uguale all’angolo in A, e il triangolo BCB’ è
rettangolo in C, si ha BC = BB'sin α , da cui segue una delle tre relazioni
trovate:
a = 2r sin α .
€
Con costruzioni analoghe si dimostra che b = 2r sin β e c = 2r sin γ , da cui segue
la relazione cercata a = b = c = 2r .
sin α €sin β
sin γ
€
€
Il teorema della corda
€
In una circonferenza
di raggio r, siano A e B gli estremi di una corda. Allora si ha:
AB = 2r sin
β
2 ,
dove β è l’angolo al centro riferito alla corda.
Alcuni risultati famosi
Il Teorema di TOLOMEO
In un quadrilatero inscritto in una circonferenza, il prodotto delle diagonali è uguale alla
somma dei prodotti dei lati opposti.
4
Dimostrazione.
Scegliamo un punto E sulla diagonale AC in modo tale che l’angolo AEB
sia uguale all’angolo BCD; per costruzione i triangoli AEB e BCD sono
simili, poiché anche gli angoli BAE e BDC sono uguali. Dall’uguaglianza
degli angoli ABE (somma degli angoli ABD e DBE) e DBC (somma degli
angoli DBE e EBC) segue l’uguaglianza degli angoli ABD e EBC.
Dall’uguaglianza degli angoli ADB e BCE, segue la similitudine dei
triangoli EBC e ABD. Quindi, dalla similitudine dei triangoli AEB e BCD
segue:
AB BD
=
⇒ AB ⋅CD = BD ⋅ AE ,
AE CD
mentre dalla similitudine dei triangoli EBC e ABD segue:
BC BD
=
⇒ AD ⋅ BC = BD ⋅ EC .
EC AD
Sommando queste relazioni otteniamo la tesi:
AB ⋅CD + AD ⋅ BC = BD ⋅ ( AE + EC ) = BD ⋅ AC
5
Osservazione. Se il quadrilatero è un trapezio isoscele, il teorema di Carnot
può essere dedotto da quello di Tolomeo.
Consideriamo nel quadrilatero ABCD il triangolo ABD, ed applichiamo il
teorema di Tolomeo:
DB ⋅ AC = AD ⋅ BC + AB ⋅CD
.
a ⋅ a = c ⋅ BC + b ⋅ b
Esprimiamo BC in modo opportuno:
BC = c − 2 b2 − a 2 sin2 β = c − 2 b2 − a 2 + a 2 cos2 β . Di conseguenza,
6
−a 2 + b2 + c 2 = 2c b2 − a 2 + a 2 cos2 β . Elevando ambo i membri al quadrato
otteniamo il teorema di CARNOT
b2 = a 2 + c 2 − 2ac cos β .
Come caso particolare è opportuno citare quello in cui il quadrilatero è un
rettangolo. In questo caso β = π e l’applicazione del teorema di Tolomeo
2
conduce al noto teorema di PITAGORA b2 = a 2 + c 2 .
"α − β %
tan $
'
a−b
# 2 &
Il teorema di Nepero: a + b = " α + β %
tan $
'
# 2 &
Dimostrazione. Dal teorema dei seni si ha
a
b
=
⇒ a sin β = bsin α .
sin α sin β
All’ultima uguaglianza si aggiungono e tolgono le quantità:
a sin β + a sin α = bsin α + a sin α ⇒ a(sin α + sin β ) = sin α (a + b) (1), e
bsin α + bsin β = a sin β + bsin β ⇒ b(sin α + sin β ) = (a + b)sin β (2).
Sottraendo la (2) dalla (1) si ottiene
(a − b)(sin α + sin β ) = (a + b)(sin α − sin β ) , e quindi
a − b sin α − sin β
. La tesi
=
a + b sin α + sin β
segue per applicazione delle formule di prostaferesi.
7
La circonferenza in coordinate polari
Problema 1
Nel piano cartesiano è data la circonferenza di centro nel punto C (1,1) e
tangente agli assi cartesiani.
a) Si scriva l’equazione cartesiana della circonferenza e delle rette ad
essa tangenti, perpendicolari alla bisettrice y = x . Si rappresentino la
circonferenza e le tangenti sul piano cartesiano, denotando con A e
A! i punti di tangenza.
(
2
) (
)
2
• L’equazione della circonferenza è x −1 + y −1 =1 . I punti di
tangenza hanno coordinate
⎧
2
2
⎛
⎪ x −1 + y −1 =1
1
1 ⎞ ⎛
1
1 ⎞
ʹ
⇒
A
1−
,1−
,
A
1+
,1+
⎨
⎜
⎟ ⎜
⎟.
⎝
2
2⎠ ⎝
2
2⎠
⎪⎩
y=x
(
) (
)
Grazie alle proprietà geometriche della circonferenza le tangenti
⎛
⎛
1
1 ⎞
1
1 ⎞
sono t : y −1+
= − ⎜ x −1+
= − ⎜ x −1−
⎟ e t ʹ : y −1−
⎟.
⎝
⎝
2
2⎠
2
2⎠
S’introduce il sistema polare con polo nel punto di coordinate cartesiane
F (1, 0 ) ed asse polare coincidente con quello delle ascisse. L’angolo θ viene
preso come di consueto, in senso antiorario.
b) Si scriva l’equazione polare della circonferenza, individuando
l’intervallo di variazione dell’angolo.
• Le equazioni di passaggio da coordinate polari a cartesiane sono le
⎧⎪ x =1+ r cosθ
seguenti: ⎨
0 ≤ θ ≤ π . L’equazione polare della
⎪⎩ y = r sinθ
8
circonferenza è quindi
2
(r cosθ +1−1) + (r sinθ −1)
2
=1 ⇒ r 2 − 2r sinθ = 0 ⇒ r = 2sinθ .
Siano P il generico punto sulla circonferenza r = 2sin θ e P! il suo
simmetrico rispetto alla retta passante per il polo e perpendicolare all’asse
polare.
c) Per quale valore di θ è massima la lunghezza della corda PP! ? Si
risponda al quesito in tre modi diversi: con argomentazioni di
carattere geometrico, mediante applicazione del teorema di Carnot
al triangolo FPP! , mediante applicazione del teorema di Tolomeo al
quadrilatero non intrecciato di vertici APA!P! .
• Soluzione con argomentazioni di tipo geometrico: la lunghezza di
una corda è massima quando coincide con un diametro, e nel caso in
π
π
questione accade quando l’angolo P ʹF̂P = ⇒ θ = .
2
4
9
• Soluzione mediante applicazione del teorema di Carnot al triangolo
2
2
2
(
)
FPP! : PP ʹ = FP + FP ʹ − 2FP ⋅ FP ʹ cos P ʹF̂P da cui segue
2
PP ʹ = 4sin2 θ + 4sin2 θ − 8sin2 θ cos π − 2θ = 8sin2 θ 1+ cos2θ
(
)
(
)
e
quindi
2
(
)
PP ʹ = 8sin2 θ 1+ cos2 θ − sin2 θ =16sin2 θ cos2 θ ⇒ PP ʹ = 4sinθ cosθ ,
π
π
⇒θ = .
2
4
• Soluzione mediante applicazione del teorema di Tolomeo al
quadrilatero non intrecciato di vertici APA!P! : osserviamo dalla
figura seguente che il quadrilatero è non intrecciato se
135° 3π
.
0 <θ <
=
2
8
che assume il valore massimo se PP ʹ = 2sin2θ = 2 ⇒ 2θ =
Per il teorema di Tolomeo PP ʹ ⋅ AAʹ = AʹP ʹ ⋅ AP + AP ʹ ⋅ AʹP , da cui
segue
⎛
⎛ 3π
⎞
⎛
⎛ 3π
⎞
π⎞
π⎞
PP ʹ ⋅ 2 = 2cos ⎜θ − ⎟ ⋅ 2cos ⎜ − θ ⎟ + 2sin ⎜θ − ⎟ ⋅ 2sin ⎜ − θ ⎟ . Si
8⎠
8⎠
⎝
⎝ 8
⎠
⎝
⎝ 8
⎠
applicano a questo punto le formule di sottrazione del coseno e si
⎛
⎞
⎛
π 3π
π⎞
+ θ ⎟ = 4 cos ⎜2θ − ⎟ ; l’espressione
ottiene PP ʹ ⋅ 2 = 4 cos ⎜θ − −
8 8
2⎠
⎝
⎠
⎝
⎛
π⎞
π
π
PP ʹ = 2cos ⎜2θ − ⎟ è massima se 2θ − = 0 ⇒ θ = .
2⎠
2
4
⎝
Problema 2
Nel piano cartesiano è data la circonferenza di centro nel punto A 1,1 e
( )
tangente agli assi cartesiani.
10
S’introduce il sistema polare con polo nell’origine O ( 0, 0 ) del sistema
cartesiano, e asse polare coincidente con quello delle ascisse. L’angolo
θ viene preso come di consueto, in senso antiorario.
a) Si scriva l’equazione polare della circonferenza applicando le
!# x = r cosθ
2
2
equazioni "
alla circonferenza ( x −1) + ( y −1) = 1 ,
#$ y = r sin θ
individuando l’intervallo di variazione dell’angolo.
•
2
(r cosθ −1) + (r sinθ −1)
2
=1 ⇒ r 2 − 2r cosθ + sinθ +1= 0 ; l’equazione
(
)
polare della circonferenza è: r = (cosθ + sinθ ) ± sin2θ , 0 ≤ θ <
π
.
2
π
indichiamo rispettivamente con D e con C
4
i due punti sulla circonferenza associati al medesimo angolo, di coordinate
polari D : r = (sinθ + cosθ ) − sin2θ ,e C : r = (sinθ + cosθ ) + sin2θ . Siano
Dʹ e C ʹ i simmetrici di D e di C rispetto alla bisettrice y = x .
b) Dopo aver verificato che Dʹ e C ʹ sono punti della circonferenza, si
applichi il teorema di Tolomeo al quadrilatero DCC ʹDʹ per calcolare
la lunghezza delle corde DʹC e DC ʹ . Verifica la correttezza del
π
risultato per valori dell’angolo θ = 0 e θ = .
4
Per valori dell’angolo 0 ≤ θ ≤
• I punti Dʹ e C ʹ stanno sulla circonferenza per costruzione, essendo
simmetrici di punti della circonferenza rispetto ad un asse passante
per il centro della stessa. I triangoli DʹC ʹC e DCC ʹ sono uguali,
avendo in comune la base CC ʹ e gli angoli C ʹDˆ ʹC ≡ C ʹD̂C , e
11
DʹCˆ ʹC ≡ DĈC ʹ ; pertanto DʹC = DC ʹ . Dall’applicazione del teorema
di Tolomeo risulta: DʹC ⋅ DC ʹ = DʹC ʹ ⋅ DC +CC ʹ ⋅ DDʹ . Calcoliamo le
singole lunghezze osservando subito che
DC = DʹC ʹ = rC − rD = 2 sin2θ , e che rC ⋅ rD =1(potenza di O rispetto alla
circonferenza…). Di conseguenza
⎛π
⎞
⎛π
⎞
⎛π
⎞
DDʹ ⋅CC ʹ = 2rD sin ⎜ − θ ⎟ ⋅ 2rC sin ⎜ − θ ⎟ = 4sin2 ⎜ − θ ⎟ = 2 1− sin2θ .
⎝4
⎠
⎝4
⎠
⎝4
⎠
(
(
) (
2 (1+ sin2θ ) .
)
)
Ricapitolando: DʹC ⋅ DC ʹ = 4sin2θ + 2 1− sin2θ = 2 1+ sin2θ . La
lunghezza delle corde è DʹC = DC ʹ =
π
è massima l’area del triangolo
4
DCP, dove il vertice P sta sulla circonferenza in corrispondenza di
π
θ= ?
4
c) Per quali valori dell’angolo 0 ≤ θ ≤
⎛π
⎞
⎛π
⎞
1
1
• Area OCP = OP ⋅OC sin ⎜ − θ ⎟ , Area ODP = OP ⋅OD sin ⎜ − θ ⎟ ,
2
2
⎝4
⎠
⎝4
⎠
di conseguenza l’area del triangolo DCP si può ottenere per
differenza:
⎛π
⎞
1
Area DCP = Area OCP − Area ODP = OP sin ⎜ − θ ⎟⎡⎣rC − rD ⎤⎦ , da
2
⎝4
⎠
(
)
(
)
(
(
)
(
)
)
12
⎞ ⎛π
⎞
1⎛ 1
1
cui segue Area DCP = ⎜
+
+1⎟ sin ⎜ − θ ⎟⎡2 sin2θ ⎤ e, di
⎦
2⎝ 2
⎠⎣
2 ⎠ ⎝4
conseguenza,
2 +1 cosθ − sinθ
2 +1⎡
Area DCP =
2 sin2θ =
cosθ − sinθ sin2θ ⎤ .
⎦
2
2
2 ⎣
Non è semplice trovare il valore dell’angolo corrispondente al valore
massimo dell’area del triangolo DCP. Tuttavia, se elevassimo al quadrato
l’espressione dell’area, otterremmo
(
(
)
)
(
)
(
)
2
⎡ Area DCP ⎤ = 3 + 2 2 ⎡ 1− sin2θ sin2θ ⎤ . Ragionando in funzione del
⎣
⎦
⎦
2 ⎣
(
)
(
)
termine sin2θ := x si tratterebbe di massimizzare una funzione tipo
y = x(1− x) = x − x 2 : una parabola con la concavità rivolta verso il basso, e
1
con il vertice nel punto di ascissa x = . Di conseguenza il quadrato
2
dell’area assumerebbe valore massimo in corrispondenza di
1
π
π
sin2θ = ⇒ 2θ = ⇒ θ = . Dal quadrato dell’area all’area “il passo è
2
6
12
breve”.
Problema 3
a) Si scriva l’equazione polare della circonferenza x 2 + y2 − 2x = 0 , nel
riferimento che ha polo nell’origine degli assi, asse polare coincidente
con quello delle ordinate, verso dell’angolo antiorario.
13
• Nel riferimento polare assegnato risulta:
⎧⎪ x = r sinθ
⇒ 2r sinθ = r 2 ⇒ r = 2sinθ .
⎨
⎩⎪ y = −r cosθ
π
si esprima l’area del triangolo AOP,
4
essendo O l’origine degli assi, A (1,−1) , e P il punto appartenente al
b) Per valori dell’angolo 0 ≤ θ <
luogo geometrico di equazione polare r = 2sinθ . Per quale valore
dell’angolo quest’area è massima?
(
)
2sinθ cosθ − sinθ 2
⎛π
⎞
1
= sinθ cosθ − sinθ .
• Area = OP sin ⎜ − θ ⎟ ⋅OA =
2
⎝4
⎠
2 2
L’area è massima quando la proiezione dell’altezza condotta da P sulla
base OA coincide con il punto medio della corda OA, ovvero quando
π
θ = (teorema dell’angolo al centro e dell’angolo alla circonferenza), e
8
sin2θ + cos2θ −1
2 −1
vale Area = sinθ cosθ − sinθ =
.
=
2
2
c) Siano P e Q punti del luogo corrispondenti ad angoli θ e 2θ , con
π
0 ≤ θ < . Indicati con P’ e Q’ i simmetrici di P e Q rispetto al punto
2
C 1,0 , si calcoli il perimetro del quadrilatero PQP 'Q ' .
(
( )
)
(
(
)
)
14
• Per costruzione il quadrilatero è un rettangolo, inoltre
ʹ = PÔQ = 2θ − θ = θ , ⇒ PQ ʹ = P ʹQ = 2cosθ ,
PQˆ Q
⇒ PQ = P ʹQ ʹ = 2sinθ . Il perimetro è quindi
⎛π
⎞
℘ θ = 4 sinθ + cosθ = 4 2 sin ⎜ + θ ⎟ , che risulta massimo in
⎝4
⎠
π
corrispondenza di θ = .
4
() (
)
Problema 4
Nel piano cartesiano è data la circonferenza di centro C 0,2 e passante per
( )
( )
il punto A 0,4 . Introdotto un sistema di riferimento polare, con il polo
coincidente con l’origine e con l’asse polare coincidente con quello delle
ascisse (verso dell’angolo antiorario):
15
a) Si scriva l’equazione cartesiana e quella polare della circonferenza,
specificando l’intervallo di variazione dell’angolo θ . Si rappresenti la
situazione sul piano cartesiano.
• Imponiamo l’appartenenza di A 0,4 alla circonferenza
( )
(
2
2
2
x − 0 + y − 2 = R 2 , ottenendo così x 2 + y − 2 = 4 . La scelta del
) (
)
(
)
⎧⎪ x = r cosθ
sistema polare conduce alle equazioni ⎨
, con 0 ≤ θ ≤ π , da cui
⎪⎩ y = r sinθ
2
segue, per sostituzione in x 2 + y − 2 = 4 , l’equazione polare r = 4sinθ .
(
)
π
, siano P e Q i punti sulla
4
circonferenza di equazione r = 4sinθ , tali che i segmenti OP e
OQ formano con l’asse polare angoli rispettivamente uguali a θ e a
π
2θ . Si calcoli l’area del quadrilatero OPQA per θ = .
6
b) Limitatamente al caso 0 ≤ θ ≤
1
• Area OPQA = Area OPQ + Area OQA = ⎡⎣OP ⋅QH +OQ ⋅ AQ ⎤⎦ , da
2
cui segue
1⎡
⎤ 1⎡
⎤
⎣OP ⋅QH +OQ ⋅ AQ ⎦ = ⎣4sinθ ⋅ (4sin2θ )sinθ + 4sin2θ ⋅ 2cos2θ ⎦ e
2
2
quindi
1⎡
2
⎤
⎣4sinθ ⋅ (4sin2θ )sinθ + 4sin2θ ⋅ 4 cos2θ ⎦ = 8cos θ sin2θ = 3 3
2
(
)
(
)
(
)
16
π
π
≤ θ ≤ , si applichi il teorema di Carnot per
4
2
calcolare la lunghezza della corda staccata dai punti P e Q di cui al
punto precedente. Per quali valori di θ la lunghezza è massima?
c) Limitatamente al caso
2
2
2
• Per il teorema di Carnot risulta PQ = OQ +OP − 2OQ ⋅OP cosθ , da
2
cui segue: PQ =16sin2 2θ +16sin2 θ − 32sin2θ ⋅ sinθ cosθ =16sin2 θ .
π
Di conseguenza, PQ = 4sinθ è massima quando θ = ⇒ PQ = 4 .
2
• Oppure: in riferimento alla figura del quesito c) possiamo considerare
il quadrilatero OPAQ inscritto nella circonferenza, ed applicare a
questo il teorema di Tolomeo:
OA ⋅ PQ = AQ ⋅OP + AP ⋅OQ
(
)
(
)
(
)
4 ⋅ PQ = −4 cos2θ 4sinθ + 4 cosθ 4sin2θ =16sin 2θ − θ .
PQ = 4sinθ
17
Problema 5
E’ data, nel piano cartesiano, la circonferenza di equazione x 2 + y2 = 4 .
( )
Introdotto un sistema di riferimento polare r,θ con polo nell’origine ed
asse polare coincidente con quello delle ascisse, verso dell’angolo
antiorario, sia P il generico punto sulla circonferenza, e Q −2,0 .
(
)
a) Indicati con P ʹ il simmetrico di P rispetto all’asse x, e con P ʹʹ il
simmetrico di P ʹ rispetto all’asse y, si rappresenti il quadrilatero
PQP ʹP ʹʹ sul piano nei seguenti 4 casi (si traccino quindi 4 grafici
distinti):
π
π
3π
3π
; 2) < θ < π ; 3)π < θ <
; 4)
< θ < 2π ;
2
2
2
2
b) Si esprima, in funzione dell’angolo θ , l’area del quadrilatero PQP ʹP ʹʹ
in ognuno dei 4 casi di cui al punto precedente;
c) Si calcolino le lunghezze dei lati del quadrilatero, e si determini il
prodotto delle lunghezze delle diagonali nei 4 casi di cui sopra.
1)0 < θ <
Problema 6
Sono dati la circonferenza di equazione x 2 + y2 =1 e il punto Q −1;0 .
(
(
)
)
Sia P cosθ ,sinθ un generico punto sulla circonferenza. Si trovino le
coordinate del punto P ʹ , simmetrico di P rispetto all’asse delle ascisse, e
del punto P ʹʹ simmetrico di P ʹ rispetto all’asse delle coordinate. Per
π
valori 0 < θ < :
2
a) Si esprima in funzione dell’angolo θ il prodotto QP ⋅QP ʹʹ . Per
quale valore dell’angolo il prodotto è massimo?
b) Si esprima, in funzione dell’angolo, l’area del quadrilatero non
intrecciato PP ʹP ʹʹQ .
c) Si esprima in funzione dell’angolo il volume della piramide
VPP ʹP ʹʹQ , di altezza OV =1.
18
“Liceo Scientifico Statale “Guido Castelnuovo”
COMPITO DI MATEMATICA
Classe IV sezione E
14/11/2015
Problema
Nel piano cartesiano è data la circonferenza di centro C 0,2 e passante per
( )
( )
il punto A 0,4 . Introdotto un sistema di riferimento polare, con il polo
coincidente con l’origine e con l’asse polare coincidente con quello delle
ascisse (verso dell’angolo antiorario):
a) Si scriva l’equazione cartesiana e quella polare della circonferenza,
specificando l’intervallo di variazione dell’angolo θ . Si rappresenti la
situazione sul piano cartesiano.
• Imponiamo l’appartenenza di A 0,4 alla circonferenza
( )
2
( x − 0) + ( y − 2)
2
2
= R 2 , ottenendo così x 2 + y − 2 = 4 . La scelta del
(
)
⎧⎪ x = r cosθ
sistema polare conduce alle equazioni ⎨
, con 0 ≤ θ ≤ π , da cui
y
=
r
sin
θ
⎪⎩
2
segue, per sostituzione in x 2 + y − 2 = 4 , l’equazione polare r = 4sinθ .
(
)
π
, siano P e Q i punti sulla
4
circonferenza di equazione r = 4sinθ , tali che i segmenti OP e
OQ formano con l’asse polare angoli rispettivamente uguali a θ e a
π
2θ . Si calcoli l’area del quadrilatero OPQA per θ = .
6
b) Limitatamente al caso 0 ≤ θ ≤
19
1
• Area OPQA = Area OPQ + Area OQA = ⎡⎣OP ⋅QH +OQ ⋅ AQ ⎤⎦ , da
2
cui segue
1⎡
⎤ = 1 ⎡4sinθ ⋅ (4sin2θ )sinθ + 4sin2θ ⋅ 2cos2θ ⎤ e
OP
⋅QH
+OQ
⋅
AQ
⎣
⎦
⎣
⎦
2
2
quindi
1⎡
2
⎤
⎣4sinθ ⋅ (4sin2θ )sinθ + 4sin2θ ⋅ 4 cos2θ ⎦ = 8cos θ sin2θ = 3 3
2
(
)
(
)
(
)
π
π
≤ θ ≤ , si applichi il teorema di Carnot per
4
2
calcolare la lunghezza della corda staccata dai punti P e Q di cui al
punto precedente. Per quali valori di θ la lunghezza è massima?
c) Limitatamente al caso
20
2
2
2
• Per il teorema di Carnot risulta PQ = OQ +OP − 2OQ ⋅OP cosθ , da
2
cui segue: PQ =16sin2 2θ +16sin2 θ − 32sin2θ ⋅ sinθ cosθ =16sin2 θ .
π
Di conseguenza, PQ = 4sinθ è massima quando θ = ⇒ PQ = 4 .
2
I problemi di trigonometria
Le conoscenze di goniometria e trigonometria fin qui acquisite permettono
di risolvere i problemi geometrici riguardanti la cosiddetta risoluzione dei
triangoli, ovvero l’espressione delle relazioni che legano tra loro i lati e gli
angoli.
Problema
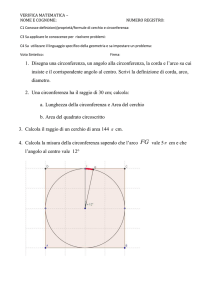
E’ data la semicirconferenza di diametro AB = 2 , r la semiretta di origine in A, e P il
punto in cui r interseca la circonferenza. Indicato con x l’angolo PAˆ B e con P’ il
simmetrico del punto P rispetto all’asse del diametro AB, si determinino:
a. La lunghezza della corda PP’€al variare di x;
€
b. L’area del triangolo POP’, dove O è il centro della semicirconferenza.
Per quali valori
di x tale
area assume il valore massimo?
c. L’area del triangolo OEP.
Soluzione
a. PAˆ B = x = APˆ O ⇒ P' Pˆ O = 2x ⇒ PP'= 2cos2x
€
21
b. Area(POP') = 1 2cos2x sin2x = sin 4 x . Tale valore è massimo quando
2
π
π
4x = ⇒ x = .
2
8
2
€
€
c.
€
1
PP' 1
2cos2x tan x cos2x
Area(OEP) = OE ⋅
= OA tan x
=
2
2
2
2
2
22
2. Sia T un punto appartenente all’arco AB congruente a un quarto della
circonferenza di centro O e raggio OA. Posto OAˆ T = x , si costruisca la funzione
AT + TB
.
f (x) =
OA
€
€
Posto il raggio OA = r si ha che AT = 2r cos x . L’angolo
π
π
π
π
BOˆ T = − (π − 2x) = 2x − , con la limitazione ≤ x < . Dal teorema del
2
2
4
2
coseno applicato al triangolo
(isoscele) BOT otteniamo
€
€
%
%
π(
π(
BT 2 = OB 2 + OT 2 − 2OB ⋅ OT cos'2x − * ⇒ BT = r 2(1− cos' 2x − * = r 2(1− sin2x) .
€
&
&
2)
2)
La
funzione cercata è dunque
€
2r cos x + r 2(1− sin2x)
1+ cos2x
=2
+ 2(1− sin2x) = 2(1+ cos2x) + 2(1− sin2x)
r
2
π
π
= 2 cos x + 2(cos2 x + sin 2 x − 2sin x cos x) = 2 cos x + 2 cos x − sin x = ( ≤ x < ) = 2 − 2 cos x + 2 sin x
4
2
'r = 8 − 4 2
')
') r 2 = 8 − 4 2
)
r sin α = 2 − 2
π
⇒(
⇒(
⇒ f (x) = 8 − 4 2 sin(x + )
(
π
8
)*tan α = 2 −1
)* r cosα = 2
)* θ =
8
f (x) =
(
(
)
)
3. Nel triangolo equilatero ABC, di lato unitario, sia P un punto sul lato BC. Detto
€
x = BAˆ P
€
23
a) Si determini la funzione
f (x) =
1
.
AP
b) Verificato che la funzione richiesta può essere scritta nella forma
2
π
f (x) =
sin(x + ) , si tracci il grafico nell’intervallo [0,2π ] .
3
€3
c) Si stabilisca per quali valori di k l’equazione
nell’intervallo [0,2π ] .
f (x) = k
ammette due soluzioni,
€
€
€
€
a) Per il teorema dei seni risulta:
" 2π
%
"π
%
sin $ − x '
2sin $ + x '
"
" 2π
%%
AP
AB
# 3
& 2
#3 &
=
⇒ f x =
=
sin $ π − $ − x '' =
" 2π
%
π
π
# 3
&&
3 #
3
sin
sin
sin $ − x '
3
3
# 3
&
()
b)
c) L’equazione ammette 2 soluzioni per
"π % 2
" 7π %
2
f 0 < k ≤ f $ '=
∧−
= f $ ' < k < f 2π .
#6&
# 6 &
3
3
()
( )
24
4. Nella semicirconferenza unitaria di diametro AC sia B il punto tale che
e sia P un punto sulla semicirconferenza con
BAˆ C =
PAˆ C := x .
π
,
6
€
€
π
π
≤x<
6
2
$
PB
π'
AP = AC cos x = 2cos x ;
= 2r = 2 ⇒ PB = 2sin& x − ) . Di
$
π'
%
6(
sin& x − )
€
%
6(
€
$
'
conseguenza, f (x) = AP + PB = 2cos x + 2sin& x − π ) . Di conseguenza
%
6(
# 3
&
1
f (x) = 2cos x +€2%
sin x − cos x ( = cos x + 3 sin x .
2
$ 2
'
€
a) Si determini la funzione
•
€
f (x) = AP + PB ,
nel caso in cui
b) Verificato che la funzione richiesta può essere scritta nella forma,
#
π&
f€(x) = 2sin% x + ( si tracci il grafico nell’intervallo [0,2π ] .
$
6'
• Con il metodo dell’angolo aggiunto è possibile scrivere la funzione
nella forma
€
% Acosα = 3 %)α = − π
€ ⇒&
f (x) = Asin( x − α ) ⇒ &
6.
)' A = ±2
' −Asin α = 1
Si determina il
valore dell’ampiezza sostituendo un valore di riferimento:
" 1%
f (0) = 1 = ±2$ ' ⇒ A = 2 . La funzione può essere scritta quindi nella forma
# 2&
#
π&
f (x) = 2sin% x + ( .
$
6'
€
€
€
25
c) Si individui il valore di x per cui è massimo il perimetro del triangolo
APB.
• Il perimetro del triangolo APB è dato dalla funzione dell’angolo
#
π&
π
p(x) = AP + PB + AB = 2sin% x + ( + 2cos . Questa espressione è
$
6'
6
massima quando l’argomento della funzione seno è uguale a
€
⇒ x+
π π
π
= ⇒x= .
6 2
3
π
:
2
€ APB e
5. Si esprima in funzione di x il rapporto tra l’area del triangolo
l’area del triangolo AOP, dove O è il centro della semicirconferenza.
• L’area del triangolo AOP è
triangolo APB è
S(AOP) =
2cos x sin x
,
2
mentre quella del
%
%
π(
π
π(
AB ⋅ AP sin' x − * 2cos ⋅ 2cos x ⋅ sin' x − *
%
π(
&
&
6€)
6
6)
S(APB) =
=
= 3 cos x ⋅ sin' x − * .
&
2
2
6)
€
Il
26
rapporto tra le aree è dato dalla funzione
r(x) =
%
π(
3
1
3 co/ s x ⋅ sin' x − *
sin x − cos x 3
3
&
6)
2
= 3 2
= −
.
co/ s x ⋅ sin x
sin x
2 2tan x
6. Un triangolo ABC è inscritto in una circonferenza di raggio r e
3
cos ACˆ B = . Determina l’ampiezza dell’angolo ABˆ C = x in modo tale
€
5
che l’area del triangolo ABC valga
€
28 2
r .
25
€
€
3
4
cos ACˆ B = ⇒ sin ACˆ B = ;
5
5
2
2
2
AC = 2r − 2r cos2x = 2r 2 (1− cos2x) ⇒ AC = 2r sin x
8
AB = 2r sin ACˆ B = r
5
6
8
BC = AC cos ACˆ B + ABcos x = r sin x + r cos x
5
5
28 2 1 2
8
r =
r(3sin x + 4 cos x) r sin x
25
25
5
2
2
6sin x + 8sin x cos x − 7(sin x + cos 2 x ) = 0
−sin 2 x + 8sin x cos x − 7cos2 x = 0
cos2 x (−tan 2 x + 8tan x − 7) = 0
tan 2 x − 8tan x + 7 = 0
tan x = 4 ± 3 ⇒ tan x = 1 ⇒ x =
€
π
4
27
7. Sia P un punto sulla circonferenza di centro l’origine e raggio
unitario, e sia Q ( 0, −1) . Si determini, al variare dell’angolo x := PÔA ,
l’area del triangolo OPQ, e si dica per quali valori di x è massima.
• Il triangolo
Area (OPQ ) =
OPQ
è isoscele poiché
OQ ⋅ PH 1⋅ cos x
=
2
2
OQ̂P = OP̂Q =
π x
− .
4 2
. L’area è massima per
x=0,
valore
dell’angolo a cui corrisponde il valore del coseno uguale a uno.
Esercizi
1. In un generico rettangolo, si indichi con x l’angolo che una diagonale
forma con un lato. Si esprima in funzione di x il rapporto tra i raggi
delle due circonferenze inscritte nei triangoli isosceli individuati dalle
due diagonali. Sempre in funzione di x, si esprima la lunghezza del
segmento d congiungente i centri delle due circonferenze.
2
•
2
"b
% "a %
r 1+ cos x
b
= tan x ⇒ 1 =
, d = $ − r2 ' + $ − r1 '
a
r2 1+ sin x
#2 & #2 &
2. Sulla semiretta s di origine O si segni il punto H a distanza b da O, e
si conduca per esso la perpendicolare p a s. Sia t la semiretta con origine
nel medesimo punto O, che incontra p nel punto P, e sia x := PÔH .
Indicata con n la perpendicolare al segmento PO condotta da H, sia C il
punto in cui n interseca la bisettrice dell’angolo delimitato dalle
semirette t e p, con origine in P, esterno al triangolo OPH. Si esprima in
funzione di x il rapporto tra la misura del raggio della circonferenza di
centro C e tangente alle semirette p e t, e quella dell’altezza del triangolo
CPH riferita alla base CH.
28
•
!π x$
r
= tan # + &
" 4 2%
h
3. Indicato con O un vertice di un cubo, sia P un punto su uno spigolo
opposto ad O, di vertici A e B. Congiungiamo P con un vertice Q di
una faccia avente in comune con quella a cui appartengono O e P lo
spigolo di estremi A e B. Si determini la funzione f (x) = OP + PQ in
funzione dell’angolo x = AÔP . Per quale valore dell’angolo la funzione
assume il valore minimo?
"
%
2
f (x) = l $ 1+ 1− tan x + 1+ tan2 x '
#
&
"1%
l
tan xmin = ⇒ xmin = tan −1 $ ' ⇒ f (xmin ) = l 5
2l
#2&
(
)
4. In una circonferenza unitaria si traccino due corde aventi un estremo
in comune, ed aventi lunghezza AB = 3 e BC = 2 . Preso un punto D
sull’arco AC che non contiene B, si ponga DÂC := x e se ne individuino i
limiti geometrici. Tracciate le diagonali AC e DB del quadrilatero
ABCD:
a. Si trovino le ampiezze degli otto angoli che vengono a formarsi;
b. Si determini la posizione di D che rende massima la lunghezza
della diagonale DB;
c. Si dica per quali valori di x risulta DB = DC .
• a) vedi figura.
29
• I limiti geometrici possono essere individuati ragionando sulla somma
degli angoli interni al triangolo DAC: 180° =105° + x + DĈA , da cui
segue che x = 0 se D ≡ C , e x = 75° se D ≡ A . Di conseguenza
0° < x < 75° .
• b) La lunghezza della diagonale DB si trova con il teorema della
corda: DB = 2sin (45° + x ) . Tale lunghezza è massima se
45° + x = 90° ⇒ x = 45° .
• c) Si ha
x = x + 45° ⇒ impossibile
DB = DC ⇔ 2sin(45° + x) = 2sin x ⇔
180° − x = 45° + x ⇒ x =
.
135°
= 67,5°
2
5. Nel triangolo ABC il lato BC misura 1 e l’ampiezza dell’angolo in A
è π . Condotte le bisettrici BM e CN, si determini per quale
3
triangolo ABC risulta minima la somma dei raggi delle circonferenze
circoscritte ai triangoli BNC e BMC.
€
π x
− . Si applichi il teorema della corda
3 2
!x π $
" x 2π %
ai triangoli BCM, dove 2r1 sin # + & , e BCN, dove 2r2 sin $ − + ' .
"2 3 %
# 2 3 &
1
Allora r1 + r2 := f (x) =
è minima quando il denominatore assume
!π x$
sin # + &
" 3 2%
π
il valore massimo, ovvero 1, x = ]
3
[Si ponga CB̂A := x ⇒ BĈA =
30
6. Un triangolo A B C, isoscele sulla base BC, ha area costante s 2 . Si
determini, in funzione dell’ampiezza dell’angolo al vertice, il
prodotto R ⋅ r del raggio R della circonferenza circoscritta e del
raggio r della circonferenza inscritta.
"π
x%
2&
x
2
[Per il teorema della corda risulta AB = AC = 2R sin $ − ' = 2R cos , dove R
#2
è il raggio della circonferenza circoscritta. Scriviamo l’area come somma
delle aree dei triangoli AOB, AOC, e BOC, dove O è il centro della
x
circonferenza inscritta: s = 2Rr cos + Rr sin x ⇒ Rr := f (x) =
2
2
s2
].
x
2cos + sin x
2
8. In un quadrato ABCD di lato l, la semiretta condotta dal vertice A
interseca il lato BC in un punto P. Sia x := PÂB .
31
• Si dimostri che
DP = l tan 2 x − 2 tan x + 2 . Posto y := PD̂C = DP̂F si ha:
l
DP sin y = l − AP sin x = l −
sin x = l − l tan x
. Sommando in quadratura
cos x
DP cos y = l
2
la tesi: DP = l 2 "#1+ (1− tan x )2 $%
si ha
• Si calcoli la misura del raggio della circonferenza inscritta nel
triangolo APC. Sia E il centro della circonferenza. Si ha
S ( APC ) = S ( AEC ) + S ( AEP ) + S ( PEC ) , da cui segue
%
l2
r"
l
1− tan x
+ l (1− tan x ) ' ⇒ r =
.
(1− tan x ) = $# l 2 +
&
2
2
cos x
1+ 2 − tan x + cos x
• Si dimostri che il perimetro del triangolo
ADP è
minimo per
tan x =
1
.
2
Sia A’ il simmetrico di A rispetto a B. Il segmento DA’ taglia il lato
BC nel punto medio. Sia P* il punto medio; allora il triangolo ADP*
ha perimetro minimo. Infatti, ogni altro triangolo ADP è tale che
AP + PD > DA' = DP * + P * A' = DP * + P * A .
9. Sarebbe stato possibile determinare DP nel problema precedente
utilizzando il teorema di Tolomeo?
• No, perché non è detto che il punto P passi per la circonferenza a cui
appartengono i vertici A, C, D, quindi salta l’ipotesi che il
quadrilatero si inscritto in una circonferenza.
10.
Sia ABCD un quadrilatero “non intrecciato” inscritto in una
circonferenza, e tale che AB = BC = a . Siano inoltre CD = b , DA = c ≠ b , e
AD̂C := 2x .
32
a) Si dimostri che la diagonale BD biseca l’angolo
• Il triangolo ABC è isoscele, quindi
AD̂C .
BÂC = BĈA ⇒ AD̂B = BĈA = BÂC = BD̂C ⇒ AD̂B = BD̂C =
AD̂C
.
2
b) Dopo aver applicato il teorema di Carnot ai triangoli ABD e BDC per trovare due
distinte espressioni di a 2 , si determini la diagonale DB.
2
•
a 2 = c 2 + DB − 2c ⋅ DB cos x
2
2
2
. Sottraendo le due espressioni membro a
a = b + DB − 2b ⋅ DB cos x
b+c
.
2 cos x
AC ⋅ DB = a ( b + c) .
membro si ha: (b − c) (b + c − 2DB cos x ) = 0 ⇒ DB =
c) Si dimostri che il prodotto delle diagonali è
• La tesi segue dall’applicazione del teorema di Tolomeo, oppure
dal calcolo diretto, essendo AC = 2a cos x .
d) Si discuta il caso b = c .
• In questo caso DÂC = DĈA = π − x , e le diagonali formano quattro
2
angoli retti, e pure gli angoli BĈD e BÂD lo sono. In particolare,
se a = b il quadrilatero è un quadrato.
Geometria e astronomia
Misura del raggio terrestre (Eratostene 275 – 195 a.C.)
Le prove della sfericità della Terra, secondo alcuni pensatori dell’antichità,
erano rappresentate dalla graduale visibilità degli oggetti che si
avvicinavano dall’orizzonte, e l’ombra della Terra proiettata sulla Luna
durante un’eclisse di Luna. Rappresentiamo schematicamente il
procedimento di misura del raggio terrestre seguito da Eratostene.
Scelte due località sullo stesso meridiano (Alessandria e Siene), distanti
⌢
AS = 785km , Eratostene misura l’ombra prodotta da un’asta verticale a
mezzogiorno in corrispondenza delle due località. L’angolo formato dai
raggi solari con la direzione dell’asta (quella del filo a piombo) è 7°12! per
la misura eseguita ad Alessandria, e circa 0° per quella eseguita a Siene. La
lontananza del Sole è tale da poter considerare i raggi solari, in
corrispondenza della superficie terrestre, approssimativamente paralleli.
33
⌢
La lunghezza dell’arco AS = 785km , e la misura dell’angolo formato dai
raggi solari con la direzione del filo a piombo
#l&
l
= tan α ⇒ α = tan −1 % ( = 7°12) , fornisce per similitudine una misura del
L
$L'
raggio terrestre, d’impressionante precisione se consideriamo i tempi in cui
è stata eseguita:
785km 7°12'
=
⇒ RT ≈ 6.250km .
2π RT 360°
Misura della distanza Terra-Luna
Si può sfruttare uno schema simile al precedente. Nella ricostruzione dello
schema di ragionamento seguito da Aristarco di Samo (310-230 a.C.), i punti
A e B sono lontani tra loro, ed il punto L, indicante la Luna, situato sulla
verticale alla superficie terrestre in B.
L’angolo α si può misurare, così come l’angolo β (quest’ultimo con un
procedimento del tutto analogo a quello seguito da Eratostene), mentre
l’angolo OL̂A := γ = α − β . La distanza OL si determina quindi applicando
sin α
il teorema dei seni al triangolo OAL : OL = RT
= 3,84 ⋅105 km
sin α − β
(
)
34
La distanza Terra-Sole
Per il calcolo di questa distanza, Aristarco partì dal presupposto che la
Luna, illuminata dal Sole, ne rifletteva la luce. Indichiamo con O un
osservatore sulla superficie terrestre che, in un certo istante, vede una metà
illuminata. La congiungente luna-osservatore è perpendicolare alla
direzione dei raggi solari che illuminano la metà della superficie della luna.
In virtù della grande distanza, i raggi solari arrivano approssimativamente
paralleli sulla superficie lunare. In particolare OL ⊥ OS ⇒ OL = OS cos α .
Sapendo che OL = 3,84 ⋅105 km , e che α = 89°50! , si ottiene per la distanza
Terra-Sole il valore OS =1,32⋅108 km . Per la cronaca, il valore dell’angolo
α = 89°50' è quello ottenuto in epoca moderna. Il valore misurato da
Aristarco era α = 87° : uno scarto di 2,85° che in termini di coseno
35
dell’angolo significa una sottostima della distanza terra-sole dell’ordine di
10.
La distanza Venere-Sole (pianeta interno)
Si assume che Terra e Venere si muovono su orbite circolari, complanari e
concentriche rispetto al Sole. Da svariate misure eseguite è noto che
l’angolo massimo tra le semirette congiungenti la Terra e il Sole, e la Terra
ˆ = 46° . In corrispondenza di quest’angolo quindi, la
e venere, è α :=VTS
semiretta TV è approssimativamente tangente all’orbita di Venere.
Definita l’unità astronomica come la distanza Terra-Sole ( TS =1,49 ⋅108 km ), si
ha per la distanza Venere-Sole il valore VS = 0,72TS .
La distanza Giove – Sole (pianeta esterno)
Anche in questo caso si assume che il moto di Giove sia circolare uniforme,
complanare con l’orbita terrestre, concentrica con questa rispetto al Sole.
Scegliamo come riferimento il sistema delle stelle fisse, ed indichiamo con
2α l’arco di orbita percorsa da Giove in un certo tempo rispetto alle stelle
fisse, con 2β l’arco percorso, sempre da Giove nel medesimo tempo,
rispetto al Sole, e con 2γ l’arco percorso dalla Terra, rispetto al Sole,
sempre nello stesso intervallo di tempo t. Misurata l’altezza di Giove
sull’orizzonte, δ , si applica il teorema dei seni al triangolo SG1T1 :
36
G1S
T1S
cos δ
=
⇒ G1S =
T S , dove T è il
!π
$
!π
$
! πt
$ 1
sin # + δ & sin # + β − (γ + δ ) &
cos # − ( π t + δ ) &
"2
%
"2
%
"T
%
periodo di Giove, t è la durata del transito
G1G2
e
t :1a = 2γ : 2π ⇒ 2γ = 2π t
t :T = 2β : 2π ⇒ 2β =
2π t
T
T1T2