Competenza matematica Specifico formativo della

CURRICOLO MATEMATICA
COMPETENZA CHIAVE EUROPEA: Competenza matematica
Specifico formativo della disciplina:
L’insegnamento della Matematica è finalizzato a dare strumenti per la descrizione scientifica del mondo e per affrontare i problemi della vita quotidiana.
Contribuisce a sviluppare la capacità di comunicare e discutere, di argomentare in modo corretto, di comprendere i punti di vista e le argomentazioni degli altri.
ABILITA’ DI BASE
1.
2.
3.
4.
Rappresentare
Calcolare e misurare
Argomentare e spiegare
Risolvere problemi
RUBRICA VALUTATIVA
COMPETENZA MATEMATICA
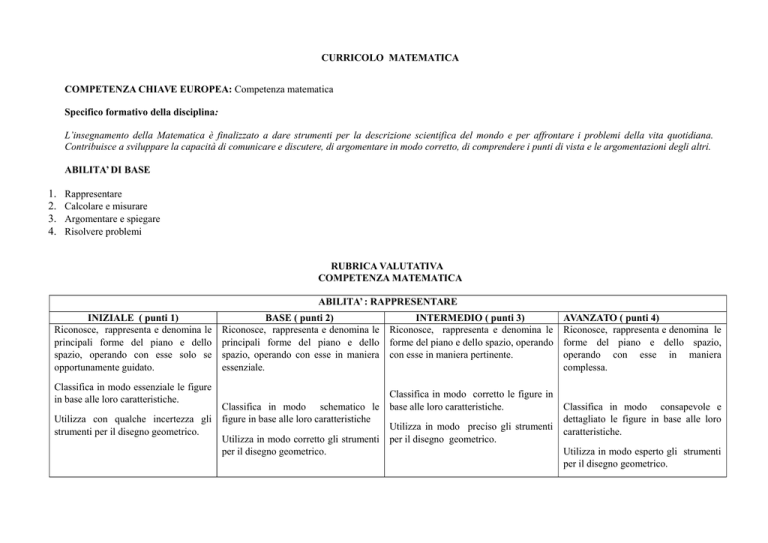
ABILITA’ : RAPPRESENTARE
INIZIALE ( punti 1)
Riconosce, rappresenta e denomina le
principali forme del piano e dello
spazio, operando con esse solo se
opportunamente guidato.
Classifica in modo essenziale le figure
in base alle loro caratteristiche.
Utilizza con qualche incertezza gli
strumenti per il disegno geometrico.
BASE ( punti 2)
Riconosce, rappresenta e denomina le
principali forme del piano e dello
spazio, operando con esse in maniera
essenziale.
Classifica in modo schematico le
figure in base alle loro caratteristiche
Utilizza in modo corretto gli strumenti
per il disegno geometrico.
INTERMEDIO ( punti 3)
Riconosce, rappresenta e denomina le
forme del piano e dello spazio, operando
con esse in maniera pertinente.
Classifica in modo corretto le figure in
base alle loro caratteristiche.
Utilizza in modo preciso gli strumenti
per il disegno geometrico.
AVANZATO ( punti 4)
Riconosce, rappresenta e denomina le
forme del piano e dello spazio,
operando con esse in maniera
complessa.
Classifica in modo consapevole e
dettagliato le figure in base alle loro
caratteristiche.
Utilizza in modo esperto gli strumenti
per il disegno geometrico.
ABILITA’: CALCOLARE E MISURARE
INIZIALE ( punti 1)
Legge e scrive, riconosce, confronta,
rappresenta i numeri ed esegue
algoritmi in modo essenziale, ma con
qualche incertezza e talvolta necessita
di guida.
BASE ( punti 2)
Legge e scrive, riconosce, confronta,
rappresenta i numeri ed esegue
algoritmi in modo sostanzialmente
corretto.
INTERMEDIO ( punti 3)
Legge e scrive, riconosce, confronta,
rappresenta i numeri ed esegue algoritmi
con sicurezza e in modo generalmente
accurato.
AVANZATO ( punti 4)
Legge e scrive, riconosce, confronta,
rappresenta i numeri ed esegue
algoritmi con metodo sicuro e in modo
critico, accurato e in completa
autonomia.
ABILITA’: ARGOMENTARE E SPIEGARE
INIZIALE ( punti 1)
Opportunamente guidato, raccoglie e
classifica dati, ricavando alcune
semplici informazioni.
Considera il punto di vista altrui.
BASE ( punti 2)
Effettua semplici indagini, raccoglie,
classifica ed organizza dati, ricavando
alcune informazioni.
INTERMEDIO ( punti 3)
Effettua indagini, raccoglie, classifica ed
organizza dati, li interpreta, ricavando
informazioni complete.
AVANZATO ( punti 4)
Effettua indagini, raccoglie, classifica
ed organizza dati, li interpreta in modo
critico, ricavando ed elaborando
informazioni complete.
Si confronta con il punto di vista altrui.
Formula ipotesi e si confronta con il
punto di vista altrui.
Costruisce ragionamenti, formulando
ipotesi, sostenendo le proprie idee e
confrontandosi con il punto di vista
altrui.
ABILITA’ : RISOLVERE SITUAZIONI PROBLEMATICHE
INIZIALE ( punti 1)
BASE ( punti 2)
INTERMEDIO ( punti 3)
Opportunamente guidato individua il Legge e comprende semplici testi che Legge e comprende testi che
percorso risolutivo di una semplice coinvolgono aspetti matematici.
coinvolgono aspetti logici e matematici
situazione problematica.
mantenendo il controllo sia sul processo
risolutivo, sia sui risultati.
Individua percorsi risolutivi di una
Individua percorsi risolutivi di un
situazione problematica in modo
problema in modo corretto ed in
sostanzialmente corretto.
autonomia.
Legenda:
AVANZATO ( punti 4)
Legge e comprende testi complessi che
coinvolgono aspetti logici e matematici
mantenendo il controllo sia sul
processo risolutivo, sia sui risultati.
Individua più strategie risolutive di un
problema in modo corretto ed in piena
autonomia.
Percentuale Punteggio
Voto
Fino al 49 %
6
Dal 50 % al 65 %
7
Dal 66% al 85 %
8
Dall’ 86% al 90 %
9
Dal 91% al 100 %
10
ABILITA’
DI BASE
ORDINE DI
SCUOLA
infanzia
scuola
primaria
RAPPRESENTARE
ABILITA’:
Conoscenze essenziali :
Conoscenze
ciò che l’alunno è in grado di fare
ciò che l’alunno sa
potenziate:
3 anni
▪ rappresentare esperienze vissute e situazioni con il corpo, con le parole e con  termini topologici.
simboli semplici, attribuendo loro un significato pertinente
4 anni
▪ rappresentare esperienze vissute e situazioni con il corpo, con le parole e con  termini topologici.
simboli semplici, attribuendo loro un significato pertinente e un ordine logico  semplici simboli.
(muoversi nello spazio scegliendo ed eseguendo i percorsi più idonei per  semplici percorsi.
raggiungere una meta anche sulla base di indicazioni verbali;utilizzare
correttamente termini di pertinenza matematica e geometrica quali
tanti/pochi/nessun/grande/piccolo…; disegnare oggetti e persone
5 anni
▪ rappresentare esperienze vissute e situazioni con il corpo, con le parole e  termini topologici.
consimboli semplici, attribuendo loro un significato pertinente;
 percorsi,
traiettorie,
i concetti relativi alle caratteristiche spaziali: sopra‐sotto, vicino‐lontano, davanti‐
simmetrie.
dietro, alto-basso, grande‐piccolo, di lato; un percorso in base a determinate  relazioni topologiche.
indicazioni verbali
Classe prima
 Relazioni topologiche
in situazioni concrete
 rappresentare esperienze vissute e situazioni con il corpo, con le
parole e consimboli semplici, attribuendo loro un significato pertinente (insiemi di
oggetti con diagrammi di Venn; il codice numerico corrispondente alla quantità; i
concetti relativi alle caratteristiche spaziali: sopra-sotto, vicino-ontano, davantidietro, alto basso, grande-piccolo, di lato; un percorso in base a determinate
indicazioni verbali o a mappe; eventi temporali); utilizzare calendari;




Classe seconda

▪ rappresentare esperienze vissute e situazioni con il corpo, con le parole e
consimboli semplici, attribuendo loro un significato pertinente (insiemi di oggetti

con diagrammi di Venn; il codice numerico corrispondente alla quantità;
i concetti relativi alle caratteristiche spaziali: sopra- sotto, vicino-lontano, davanti
dietro, alto- basso, grande- piccolo, di lato;
un percorso in base a determinate indicazioni verbali o a mappe; eventi temporali
e causali);
creare e utilizzare calendari;

Classe terza
 rappresentare con precisione e accuratezza la quantità attribuendo
significato: al valore posizionale delle cifre; al confronto tra numeri naturali anche



(prima, dopo, sopra,
sotto, davanti, dietro,
dentro fuori, destra,
sinistra)
Conteggio
e
rappresentazione
numerica
Precedente
–
successivo, relazioni <,
>, = in situazioni
concrete
Relazioni univoche
Struttura del problema:
dati, domanda, parola
chiave
esplicita,
rappresentazione
grafica (addizione e
sottrazione)
Precedente
–
successivo;
relazioni
<, >, = con materiale
Unità,
decine
e
centinaia con materiale
Direzione e posizione
delle linee del piano
( orizzontale, verticale,
obliqua)
Struttura del problema
(algoritmo):
dati,
domanda, parola chiave
esplicita,
rappresentazione
grafica
Il sistema posizionale
Linee, rette, semirette
Angoli con campioni 
dati
Angoli
rappresentati su una retta entro il 9999; ai dati in una tabella; alle equivalenze; alle
principali figure piane e agli elementi significativi (simmetria, angoli)





Classe quarta
 rappresentare con sicurezza e precisione il valore posizionale delle
cifre dopo il 9999; operando anche con le frazioni e con numeri decimali; usando
correttamente il S.M.D; distinguendo tra loro le principali figure piane e le loro
caratteristiche;






Classe quinta
 rappresentare in modi diversi, con sicurezza e precisione quantità:
utilizzando scomposizioni polinomiali, potenze, sistema metrico decimale,
percentuali, numeri relativi; classificando oggetti, numeri, realizzando adeguate
rappresentazioni (tabelle, istogrammi, ideogrammi); descrivendo e costruendo
relazioni significative (analogia, regolarità) nelle figure geometriche regolari
conosciute (angolo, altezza, diagonale, perimetro, area) e riconoscendo di esse le
proprietà (isoperimetria, equiestensione, simmetrie…), usando ove necessario
strumenti per il disegno geometrico.





Figure solide e piane

Poligoni e non poligoni
unità
di
misura

arbitrarie
Statistica: eventi certi,
possibili, impossibili
Algoritmo
di
un 
problema
numeri interi
e
decimali
Simmetria
Classificazione
di
elementi,
figure,
numeri in base a una
determinata proprietà
rappresentazioni di dati
la moda, la media
Frazioni
equivalenti
con
materiale
e
rappresentazione
grafica complementari,
frazione di un numero,
dalla frazione decimale
al numero decimale
numeri interi e decimali
frazioni
equivalenti,
complementari,
proprie,
improprie,
apparenti, decimali in
situazioni concrete
poligoni regolari
equiestensione e area
dei poligoni regolari
istogramma,




disegno
geometrico
unità di misura
convenzionali
linguaggio
specifico logicoprobabilistico
grandi
numeri
interi e decimali
frazioni
equivalenti,
complementari,
proprie, improprie,
apparenti, decimali
poligoni regolari e
irregolari
equiestensione e


scuola
secondaria
Classe prima
 rappresentare con precisione e accuratezza i concetti propri della
notazione esponenziale, la fattorizzazione, l’insieme dei numeri razionali, gli enti
e le figure geometriche piane
Classe seconda
 rappresentare con precisione e accuratezza quantità utilizzando
concetti di numeri razionali ed irrazionali, di proporzioni; l’equivalenza di figure
piane, tra cui la circonferenza








Classe terza
 rappresentare con precisione e accuratezza l’insieme dei numeri reali
utilizzando la scrittura polinomiale, le equazioni, il piano cartesiano e le tre
dimensioni dello spazio
ABILITA’ DI CALCOLARE E MISURARE
BASE
infanzia
3 anni
▪ calcolare :oggetti accompagnando la conta con i gesti dell’indicare
4 anni






aereogramma,
ideogramma, frecce di
relazioni
situazioni
problematiche
e 
strategie di soluzione
numeri negativi in

situazioni concrete
area dei poligoni
regolari
e
composti
notazione esponenziale, 
la fattorizzazione,
numeri razionali,
enti
e
figure
geometriche piane;
numero razionale ed
irrazionale,
le proporzioni;
le
funzioni
e
l’equivalenza di figure
piane,
la circonferenza;
I grafici e le
rappresentazioni
grafiche
della
realtà
insieme dei numeri 
reali,
la scrittura polinomiale, 
le equazioni,
il piano cartesiano
le tre dimensioni dello
spazio;
Rappresentare
semplici funzioni
I poliedri regolari
calendario giornaliero.
Circonferenza
cerchio
e
numeri negativi
scuola
primaria
▪ calcolare :ragionare sulla numerosità di oggetti diversi, contare oggetti
accompagnando la conta con i gesti dell’indicare;confrontare, raggruppare e
ordinare secondo criteri diversi, identificandone alcune proprietà;
5 anni
▪ calcolare e misurare: ragionare sulla quantità e sulla numerosità di oggetti
diversi, contare oggetti o eventi accompagnando la conta con i gesti dell’indicare,
del togliere e dell’aggiungere; conoscere la sequenza numerica fino al 10 e
intuisce la successiva progressione; suddividere in parti i materiali, confrontare,
raggruppare e ordinare secondo criteri diversi,
identificandone
alcune
proprietà;confrontare e valutare quantità (più alto di, più pesante di, più
grande/più piccolo …);eseguire le prime misurazioni di lunghezze, pesi ed altre
quantità avvalendosi delle necessarie strategie
Classe prima
▪ calcolare: ragionare sulla quantità e sulla numerosità di oggetti diversi; contare
oggetti o eventi accompagnando la conta con i gesti dell’indicare, del togliere e
dell’aggiungere; conoscere la sequenza numerica fino al 20 e intuire la successiva
progressione; impiegare correttamente le strategie del contare e dell’operare con i
numeri, attribuendo ad ogni oggetto un numero, costruendo corrispondenze
biunivoche tra parola, gesto e oggetto e operando partizioni tra “oggetti contati” e
“ancora da contare”; suddividere in parti i materiali, confrontarli , raggrupparli e
ordinarli secondo criteri diversi, identificare alcune proprietà, confrontare e
valutare quantità (più alto di, più pesante di , più grande/più piccolo …);eseguire
le prime misurazioni di lunghezze, pesi ed altre quantità avvalendosi delle
necessarie strategie
Classe seconda
▪ calcolare: ragionare sulla quantità e sulla numerosità di oggetti diversi, contare
oggetti o eventi accompagnando la conta con i gesti dell’indicare, del togliere e
dell’aggiungere; conoscere la sequenza numerica fino al 100 e intuire la
successiva progressione; impiegare correttamente le strategie del contare e
dell’operare con i numeri, attribuendo ad ogni oggetto un numero, costruendo
corrispondenze biunivoche tra parola, gesto e oggetto e operando partizioni tra
“oggetti contati” e “ancora da contare”;suddividere in parti i materiali,
confrontarli, raggrupparli e ordinarli secondo criteri diversi, identificare alcune
proprietà;confrontare e valutare quantità (più alto di, più pesante di , più
grande/più piccolo …);eseguire le prime misurazioni di lunghezze, pesi ed altre
quantità avvalendosi delle necessarie strategie


presenze/assenze
associazione



presenze/assenze
calendario giornaliero.
caratteristiche
di
oggetti.

Addizione come unione
e sottrazione come
resto
la decina






Le
funzioni
di
addizione e sottrazione;
calcolo in colonna
la
funzione
della
moltiplicazione;
calcolo in colonna
Struttura del problema
(algoritmo):
dati,
domanda, parola chiave
esplicita,
rappresentazione
grafica
Classe terza
 calcolare e misurare con sicurezza e accuratezza applicando il
valore posizionale delle cifre entro il 1000, facendo calcoli, anche mentalmente,
con numeri naturali entro il 9999; effettuando confronti usando i segni di
maggiore (>), di minore (<) e di uguaglianza (=); effettuando calcoli orali e scritti
ed eseguire operazioni aritmetiche entro il 1000 (moltiplicazione con 2 cifre al
moltiplicatore), e oltre il 1000; moltiplicando e dividendo per 10, 100, 1000


Sistema posizionale

Algoritmo
delle
operazioni

Funzione dell’operatore 
frazionario in situazioni

concrete



Classe quarta
● calcolare e misurare con sicurezza e accuratezza usando, correttamente e
sempre più velocemente, la procedura delle quattro operazioni con i numeri interi
e decimali; eseguendo divisioni a 2 cifre al divisore; ricavando il perimetro delle
principali figure piane

Semplici indagini

Algoritmo
problema






del
Addizione, sottrazione,
con i numeri interi e
decimali.
Moltiplicazione
e
divisione
con
il
divisore a due cifre con
i numeri interi
Proprietà
delle
operazioni (associativa,
commutativa).
Multipli e divisori
Frazioni
complementari,
la
frazione di un numero,
dalla frazione decimale
al numero decimale
Gli angoli e ampiezza
(retto, piatto, giro,
acuto, ottuso)


Valore dello zero e
dell’uno
nelle
operazioni
affrontate
Proprietà
delle
operazioni
funzione
dell’operatore
frazionario;
terminologia;
funzione
della
virgola
nei
decimali
disegno
geometrico
indagine e la moda





Classe quinta
 calcolare e misurare con sicurezza e accuratezza usando numeri
naturali (multipli, divisori, primi, media aritmetica e di frequenza …); eseguendo
le 4 operazioni anche con i numeri decimali (divisioni con due cifre al divisore,
potenze...); confrontando e ordinando frazioni più semplici (proprie, improprie ...);
applicando le proprietà delle 4 operazioni (percentuale e sconto); usando sistemi e
unità di misura (metro quadrato, equivalenze)








Disegno
geometrico
(rettilinee, triangoli e
quadrilateri)
Poligoni
regolari
(triangolo equilatero e
quadrato),
Formule dirette per il
perimetro,
isoperimetria
Misure di lunghezza,
massa,
capacità
e
valore
Dati, moda, media
Frazione di un numero
Frazioni decimali e loro
percentuali
Addizione, sottrazione,
moltiplicazione
e
divisione
con
il
divisore a due cifre con
i numeri interi e
decimali
Proprietà
delle
operazioni
Multipli e divisori
Misure di lunghezza,
peso/massa, capacità,
valore, superficie
moda,
media
aritmetica, regolarità di
sequenze
situazioni
problematiche:
1domanda,
2
operazioni (diagramma

Percentuali

Addizione,
sottrazione,
moltiplicazione e
divisione con il
divisore a più cifre
con i numeri interi
e decimali
Prova
delle
operazioni
Criteri
di
divisibilità
Misure di tempo,




situazioni
problematiche con
più
operazioni
(diagramma
di
flusso,
espressioni…)
di
espressioni…)
scuola
secondaria
Classe prima
 calcolare e misurare con accuratezza e precisione seguendo algoritmi
contenenti potenze e loro proprietà, frazioni o numeri fattorizzati
Classe seconda
 calcolare e misurare con accuratezza e precisione ed algoritmi
contenenti radici, proporzioni e loro proprietà
flusso,


potenze e proprietà,
frazioni o numeri
fattorizzati.

radici, proporzioni
e proprietà;

principi del calcolo
polinomiali e delle
equazioni;
Classe terza
 calcolare e misurare con accuratezza e precisione per ricercare
risultati di espressioni polinomiali ed equazioni
ABILITA’ DI ARGOMENTARE E SPIEGARE
BASE
infanzia
3 anni
▪ argomentare e spiegare: guardare la realtà e raccontarla con semplici parole
4 anni
▪ argomentare e spiegare: cominciare ad osservare la realtà, interrogarsi ed
interpretare a modo suo le situazioni concrete della vita quotidiana
5 anni
▪ argomentare e spiegare: osservare la realtà, rilevare aspetti problematici,
formulare possibili ipotesi risolutive spiegando le proprie idee al riguardo e
confrontandosi con gli altri
Scuola
Classe prima
primaria
▪ argomentare e spiegare: osservare la realtà, rilevare aspetti problematici,
formulare possibili ipotesi risolutive spiegando le proprie idee al riguardo e
confrontandosi con gli altri



semplici termini

differenze del vissuto
quotidiano.


realtà che ci circonda
semplici problemi.
Figure solide e piane
Struttura del problema:
dati,
domanda,
rappresentazione
grafica e parola chiave

La
proporzionalit
à diretta e
inversa
esplicita (addizione e
sottrazione)
Classe seconda
 argomentare e spiegare: osservare la realtà, rilevare aspetti
problematici, formulare possibili ipotesi risolutive spiegando le proprie idee al
riguardo e accettando il confronto con gli altri cominciando a verificarne la
tenuta



Classe terza
● argomentare e spiegare con chiarezza i procedimenti risolutivi seguiti e
confrontarli con altre possibili soluzioni


Lunghezza, capacità,
peso, tempo.
Quantificatori
indefiniti
( pochi,
alcuni,
tanti...)
possibile, impossibile,
certo
Struttura del problema
(algoritmo):
dati,
domanda,
parola
chiave
esplicita,
rappresentazione
grafica
Algoritmo
delle
operazioni
Probabilità:
eventi
certi,
possibili,
impossibili






Dati espliciti, impliciti
Domanda esplicita
Algoritmo
del
problema
Simmetria, traslazione
Classe quarta
 argomentare e spiegare con chiarezza il procedimento risolutivo seguito
e confrontarlo con altre possibili soluzioni


Il testo del problema,
dati,
le
domande
esplicite, parole chiave
esplicite ed implicite.
Classe quinta
 argomentare e spiegare in modo chiaro e preciso il procedimento

Il testo del problema,
dati,
le
domande

Linguaggio specifico
logico-probabilistico
Probabilità:
eventi
certi,
possibili,
impossibili
Dati
espliciti,
impliciti, mancanti,
superflui
Domanda esplicita,
implicita
risolutivo seguito e sa confrontarlo con altre possibili soluzioni
scuola
secondaria
Classe prima
 argomentare e spiegare le proprie conclusioni attraverso i concetti
di divisibilità, di elevamento a potenza, del numero razionale e di varie
rappresentazioni utilizzando le proprietà della geometria piana (utilizzando
segmenti, angoli, aree e perimetri di poligoni come triangoli e quadrilateri)
esplicite ed implicite,
parole chiave esplicite
ed implicite.


Classe seconda
 argomentare e spiegare conclusioni attraverso i concetti di
irrazionalità, proporzionalità diretta ed inversa e i principali teoremi della
geometria piana


Classe terza
 argomentare e spiegare: i concetti di numero relativo, il calcolo
letterale, la probabilità e la geometria solida




ABILITA’ DI RISOLVERE PROBLEMI
BASE
infanzia
3 anni
▪ risolvere problemi: affrontare piccoli problemi durante le routinesdella
giornata scolastica
4 anni
▪ risolvere problemi: cominciare ad affrontare e risolvere problemi durante le
routinesdella giornata scolastica (conta gli amici presenti e assenti, apparecchia
la tavola, distribuisce il materiale scolastico ai compagni, conta oggetti in senso
progressivo)
concetti di divisibilità,
di elevamento a
potenza, del numero
razionale, di varie
rappresentazioni
proprietà della
geometria
concetti di
irrazionalità,
proporzionalità diretta
ed inversa
principali teoremi della
geometria piana.
concetti di numero
relativo,
calcolo letterale,
la probabilità
geometria solida;

misure e distanze nello
spazio.

misure e distanze nello
spazio.
Localizzazione
di
oggetti in base ad un

riferimento.
scuola
primaria
5 anni
▪ risolvere problemi: cogliere problematiche nelle esperienze di vita
quotidiana che implicano processi di quantificazione, misurazione, previsione
(di più/di meno, uguale, maggiore/minore …) e che riguardino la collocazione
del proprio corpo nello spazio rispetto a oggetti
Classe prima
 analizzare e risolvere problemi: cogliere problematiche nelle
esperienze di vita quotidiana che implichino processi di quantificazione,
misurazione (di più/di meno, uguale, maggiore/minore …) o che riguardino la
collocazione del proprio corpo nello spazio rispetto a oggetti e ipotizzare
possibili soluzioni
Classe seconda
 risolvere problemi: cogliere problematiche nelle esperienze di vita
quotidiana che implichino processi di quantificazione, misurazione, previsione
(di più/di meno, uguale, maggiore/minore …), o che riguardino la collocazione
del proprio corpo nello spazio rispetto a oggetti, rappresentarle graficamente
e ipotizzare possibili soluzioni
Classe terza
 risolvere problemi semplici di vita reale o formulati
astraendo
dal quotidiano che implichino processi di quantificazione,
misurazione, previsione con le conoscenze di cui si dispone: riflettere con
calma e attenzione sui dati del problema, tradurli in rappresentazioni
matematiche; partendo dall’analisi di un problema, individuare le informazioni
necessarie per raggiungere un obiettivo, ipotizzare e organizzare un percorso
di soluzione, calcolare procedendo in modo ordinato
Classe quarta
 risolvere problemi semplici di vita reale
(compravendita, costo unitario, costo totale, peso netto, tara, peso lordo e
misure) con le conoscenze di cui si dispone sia numeriche che geometriche.
Riflettere con calma e attenzione sui dati del problema, tradurli in
rappresentazioni matematiche. Partendo dall’analisi di un problema,
individuare le informazioni necessarie per raggiungere un obiettivo, ipotizzare




estensioni spaziali.
proprietà con termini
quantificatori.
ipotesi e previsioni.
Struttura del problema:
dati,
domanda,
rappresentazione
grafica e parola chiave
esplicita (addizione e
sottrazione)

Struttura del problema
(algoritmo):
dati,
domanda,
rappresentazione
grafica e parola chiave
esplicita
(
addizione,
sottrazione,
moltiplicazione)
Dati espliciti, impliciti

Domanda esplicita





Algoritmo
problema
del

Testo del problema,
dati (utili, superflui,
impliciti, mancanti) e
le incognite (domande
esplicite, implicite)
Dati
impliciti,
superflui
Domanda
implicita
espliciti,
mancanti,
esplicita,
e organizzare un percorso di soluzione, calcolare con precisione procedendo in
modo ordinato
scuola
secondaria
Classe quinta
● risolvere problemi semplici (con almeno 2 domande) di vita reale
utilizzando le 4 operazioni: accettare la sfida e controllare l’impulsività,
riflettere con calma e attenzione sui dati del problema e tradurli in
rappresentazioni matematiche;
partire dall’analisi di un problema, individuare le informazioni necessarie per
raggiungere un obiettivo, ipotizzare e organizzare un percorso di soluzione,
calcolare con precisione, anche con l’ausilio di strumenti tecnologici,
procedendo in modo ordinato, e verificare i risultati conseguiti con precisione e
accuratezza.
Classe prima
 risolvere problemi di vita reale che richiedono l’uso di potenze
M.C.D e m.c.m. , frazioni, angoli, rette e poligoni, (come: calcolare il numero
di individui di una popolazione con crescita esponenziale dopo un certo
numero di generazioni; calcolare la sovrapposizione di turni con differente
periodicità; suddividere un certo numero di oggetti in gruppi senza sprechi e
ottimizzando al massimo le risorse a disposizione), perseverando per superare
difficoltà ed errori e migliorandosi continuamente nella ricerca della soluzione.
Accettare la sfida e controllare l’impulsività riflettendo con calma e attenzione
sui dati del problema, tradurli in rappresentazioni matematiche. Partendo
dall’analisi di un problema, individuare le informazioni necessarie per
raggiungere un obiettivo, ipotizzare e organizzare un percorso di soluzione,
calcolare con precisione procedendo in modo ordinato e verificare i risultati
conseguiti con precisione e accuratezza
Classe seconda
 risolvere problemi di vita reale che richiedono l’utilizzo di numeri
decimali periodici semplici e misti, radici, proporzioni e teoremi perseverando
nella ricerca della soluzione (Come calcolare percentuali e tassi di interesse;
ottenere risultati esatti attraverso la trasformazione di numeri decimali in
frazioni; calcolare, per esempio, quanto deve essere lunga una scala per
raggiungere una certa altezza, tenendo conto dell’inclinazione adeguata perché
non cada).
Accettare la sfida e controllare l’impulsività riflettendo con calma e attenzione

Situazioni
problematiche
e
strategie
risolutive
(diagramma di flusso,
espressione…)
sui dati del problema, tradurli in rappresentazioni matematiche. Partendo
dall’analisi di un problema, individua le informazioni necessarie per
raggiungere un obiettivo, ipotizzare e organizzare un percorso di soluzione,
calcolare con precisione procedendo in modo ordinato e verificare i risultati
conseguiti con precisione e accuratezza
Classe terza
 risolvere problemi di vita reale che richiedono l’utilizzo di polinomi,
equazioni, poliedri e corpi rotondi, perseverando nella ricerca della soluzione
(risolvere qualsiasi problema pratico che preveda l’utilizzo di una incognita;
calcolare la volumetria di recipienti) . Accetta la sfida e controlla l’impulsività
riflettendo con calma e attenzione sui dati del problema, tradurli in
rappresentazioni matematiche.
Partendo dall’analisi di un problema, individuare le informazioni necessarie
per raggiungere un obiettivo, ipotizzare e organizzare un percorso di soluzione,
calcolare con precisione procedendo in modo ordinato e verificare i risultati
conseguiti con precisione e accuratezza
ABILITA’ DI AVERE UN ATTEGGIAMENTO POSITIVO VERSO LA MATEMATICA
BASE
infanzia
3 anni
▪ avere un atteggiamento positivo verso la matematica: mostrare piacere e
partecipazione operando e giocando con materiali strutturati e non, costruzioni,
giochi da tavolo di diverse tipologie
4 anni
▪ avere un atteggiamento positivo verso la matematica: mostrare piacere e
partecipazione operando e giocando con materiali strutturati e non, costruzioni,
giochi da tavolo di diverse tipologie (giochi che implichino l’uso del corpo…)
5 anni
▪ avere un atteggiamento positivo verso la matematica: mostrare piacere e
partecipazione operando e giocando con materiali strutturati e non, costruzioni,
giochi da tavolo di diverse tipologie (tombole, tris, gioco dell’oca …, giochi che
implichino l’uso del corpo: ruba bandiera, percorsi su quadrante TERZI,
gimkane…); mostrare curiosità e interesse per il funzionamento di macchine
scuola
Classe prima
primaria
 avere un atteggiamento positivo verso la
matematica: mostrare piacere e partecipazione operando e giocando con
materiali strutturati e non, costruzioni, giochi da tavolo di diverse tipologie
.
scuola
secondaria
(tombole, tris, gioco dell’oca …, giochi che implichino l’uso del corpo: ruba
bandiera, percorsi su quadrante TERZI, gimkane…); mostrare curiosità e interesse
per il funzionamento di macchine, strumenti di misura ed esperimenti scientifici
semplici
Classe seconda
 avere un atteggiamento positivo verso la
matematica: mostrare piacere e partecipazione operando e giocando con
materiali strutturati e non, costruzioni, giochi da tavolo di diverse tipologie
(tombole, tris, gioco dell’oca …, giochi che implichino l’uso del corpo: ruba
bandiera, percorsi su quadrante TERZI, gimkane…); mostrare curiosità e interesse
per il funzionamento di macchine, strumenti di misura ed esperimenti scientifici
Classe terza
● avere un atteggiamento positivo verso la matematica: dimostrare di intuire
sempre più, attraverso esperienze significative, che gli strumenti matematici
risultano utili per operare nella realtà e di non scoraggiarsi di fronte alle difficoltà
e agli errori, ma di voler capire e migliorarsi
Classe quarta
 avere un atteggiamento positivo verso la
matematica: dimostrare di intuire sempre più, attraverso esperienze significative,
che gli strumenti matematici risultano utili per operare nella realtà e di non
scoraggiarsi di fronte alle difficoltà e agli errori, ma di voler capire e migliorarsi
Classe quinta
 avere un atteggiamento positivo verso la matematica: dimostrare di
intuire sempre più, attraverso esperienze significative, che gli strumenti
matematici risultano utili per operare nella realtà e di non scoraggiarsi di fronte
alle difficoltà e agli errori, ma di voler capire e migliorarsi
Classe prima
 avere un atteggiamento positivo verso la matematica dimostrando
di intuire sempre più, attraverso esperienze significative che gli strumenti
matematici siano utili per operare nella realtà e di non scoraggiarsi di fronte alle
difficoltà e agli errori, ma di voler capire e migliorarsi
Classe seconda
 avere un atteggiamento positivo verso la matematica dimostrando
di intuire sempre più, attraverso esperienze significative che gli strumenti
matematici siano utili per operare nella realtà e di non scoraggiarsi di fronte alle
difficoltà e agli errori, ma di voler capire e migliorarsi
Classe terza
 avere un atteggiamento positivo verso la matematica dimostrando
di intuire sempre più, attraverso esperienze significative che gli strumenti
matematici siano utili per operare nella realtà e di non scoraggiarsi di fronte alle
difficoltà e agli errori, ma di voler capire e migliorarsi