Generalità
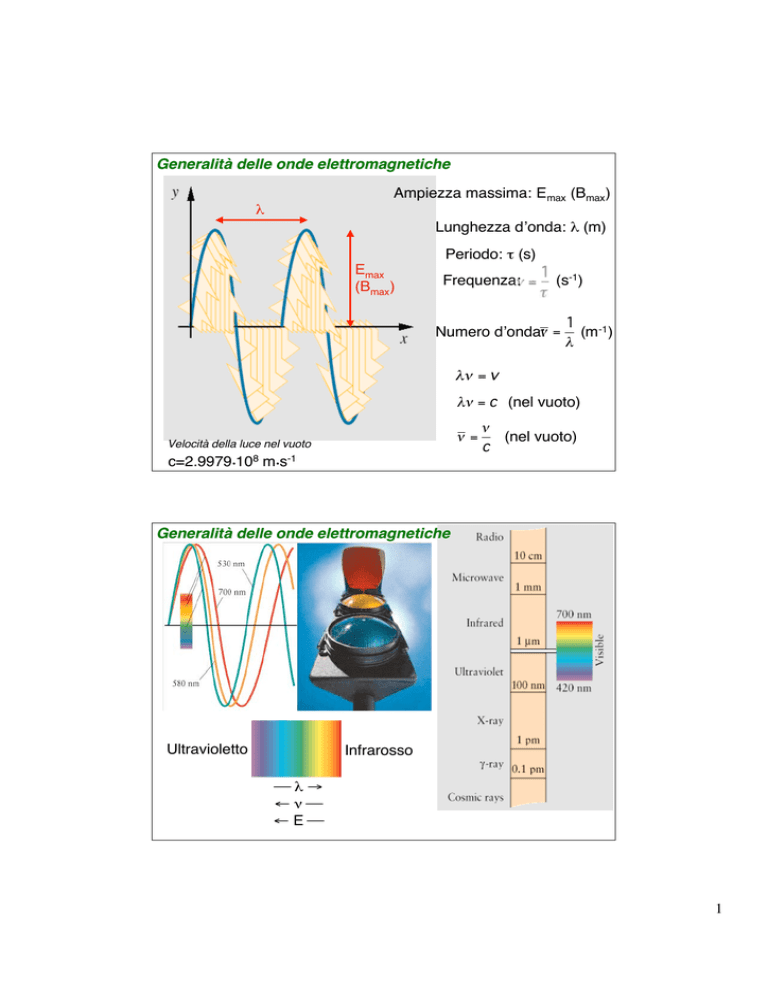
Generalità delle onde elettromagnetiche
Ampiezza massima: Emax (Bmax)
Lunghezza d’onda: (m)
Periodo: (s)
Emax
(Bmax)
Frequenza: =
1 -1
(s )
Numero d’onda: =
1
(m-1)
= v
= c (nel vuoto)
=
Velocità della luce nel vuoto
c=2.9979108 ms-1
(nel vuoto)
c
Generalità
Generalità delle onde elettromagnetiche
Ultravioletto
Infrarosso
E
1
Generalità
Generalità delle onde elettromagnetiche
La diffrazione della luce
La diffrazione della luce
2
La crisi della Fisica classica
•
•
•
•
Problemi di stabilità dimensionale degli atomi
Effetto fotoelettrico
Emissione del corpo nero
Interpretazione degli spettri di emissione degli
atomi
Struttura elettronica degli atomi
Modello
atomico di
Rutherford
--
+
+
+
---
Incompatibilità con le leggi classiche
dell’elettromagnetismo: una carica elettrica
in moto non rettilineo ed uniforme perde
progressivamente energia emettendo onde
elettromagnetiche per cui l’elettrone
collasserebbe sul nucleo in 10-11-10-12
secondi seguendo una traiettoria a spirale.
3
Emissione del corpo nero
Emissione del corpo nero
Risultati sperimentali
Previsione “classica”,
La “catastrofe ultravioletta”
4
La teoria di Planck
Scambio di energia tra materia e
radiazione elettromagnetica avviene per
“pacchetti discreti” ovvero QUANTI
E=h
h costante di Planck 6.626 x 10 -34 J s
la distribuzione delle loro energie segue la legge
statistica di Boltzmann
Effetto fotoelettrico
5
L’effetto fotoelettrico
Ema
x
h
e-
E = h > Eo
E cin = E E o = h( o )
o
Costante di Planck
h = 6.62610-34 Js
L’intensità degli elettroni emessi è proporzionale all’intensità della
radiazione incidente.
L’emissione di elettroni avviene solo se l’energia (e quindi la
frequenza) della radiazione incidente è superiore ad un certo
valore E0
L’energia cinetica è invece indipendente dall’intensità della
radiazione incidente ma dipende dalla frequenza Ecin=h(-0)
Ipotesi
di
Einstein:
radiazione
elettromagnetica costituita da particelle
(fotoni) con energia :
E = h
Nell’interazione con la materia il fotone colpendo
un atomo gli può cedere la sua energia h: se
questa è superiore all’energia necessaria per
strappare un elettrone all’atomo, l’elettrone viene
espulso ed assume energia cinetica pari alla
differenza tra l’energia del fotone incidente e la
propria energia di legame E0
6
Spettro di emissione dell’
dell’atomo di idrogeno
Spettro a righe
Analizzatore ottico
Spettro di emissione dell’
dell’atomo di idrogeno
n=
1
1
= RH 2 2 m
n Valida anche per ioni
idrogenoidi (He+, Li++, Be+++,
...
RH = 109677.76 cm-1
m = 1, 2, 3, …, n = m + 1, …, 7
L’atomo di Bohr
Base di partenza: fisica classica, in cui però Bohr
inserì i suoi due postulati.
1. Quantizzazione del raggio dell’orbita dell’elettrone
e di conseguenza dei livelli di energia;
2. Emissione (o assorbimento) di radiazione
elettromagnetica solo in corrispondenza del
passaggio da uno stato quantico ad un altro
r
-
+
Il modello atomico di Bohr:
Bohr: secondo postulato
Emissione
EA > EB
A > B
A < B
8
Lo spettro di emissione dell’idrogeno
secondo la meccanica quantistica
[da P Atkins, L. Jones Chimica Generale Zanichelli]
Il modello atomico di Bohr
h = E n ' E n "
En ' En "
h
E En "
= = n'
hc
c
=
1 2 2me4
En = 2
n
h2
Legge di Bohr
2 2me4 1
1
=
h 3c n '2 n "2 109737 cm-1
1
1
= RH 2 2 m
n RH = 109677.76 cm-1
9
Spettroscopia di emissione
Spettroscopia di assorbimento
Litio
Sodio
Potassio
Rubidio
10
Critica al modello atomico di Bohr
Uso di leggi della meccanica classica
Introduzione di postulati senza giustificazione
ORBITE di elettroni intorno al nucleo ?
Moto di un punto materiale nel piano x-y
Per conoscere la traiettoria di un corpo è necessario
conoscere posizione e velocità
velocità del punto materiale in un
dato istante
Principio di indeterminazione di Heisemberg (Nobel 1932)
È impossibile determinare con precisione
contemporaneamente la posizione e la velocità di una
particella di massa molto piccola
Effetto Compton
microscopio
microscopio
fotone
fotone
elettrone
elettrone
Principio di indeterminazione di
Per corpi di massa estremamente piccola, che si
Heisemberg
muovono a velocità prossime alla velocità della
x · (m · vx) h
luce, non è possibile conoscere con precisione la
y · (m · vy) h posizione, se è nota la quantità di moto, o
z · (m · vz) h viceversa.
11
Principio di indeterminazione di Heisemberg (Nobel 1932)
Sfera di massa m = 10-5
g
x vx h 6.6 1027erg s
=
= 6.6 1022cm2 s 1
5
m
10 g
x = 1010cm
vx = 6.6 1012cm s 1
Incertezza trascurabile
Elettrone m = 10-27 g
x vx h 6.6 1027erg s
=
= 6.6 cm2 s 1
27
m
10 g
x = 1010cm
vx = 6.6 1010cm s 1
Vx indeterminata
Le onde di De Broglie
h
=
mv
• Louis DeBroglie :
Alla propagazione di raggi elettronici si accompagna
un fenomeno ondulatorio come accade per la
propagazione dei raggi luminosi
Particella
m (g)
-28
Elettrone lento
9.1 x 10
Elettrone veloce
9.1 x 10 -28
Sferetta
10
Sferetta
1
-6
v (m s-1)
(nm)
1
7.3 x 107
5.9 x 107
1.2
0.01
6.6 x 10-12
0.01
6.6 x 10-18
12
Dualismo onda particella
Radiazione
elettromagnetica (luce)
Fascio di fotoni
Elettroni
Foglio metallico
policristallino o cristallo
1927, Davisson, Germer e Thomson
Fascio di elettroni
Dualismo onda particella
Sia il comportamento della luce che quello della
materia può essere spiegato in alcuni casi
considerandole come particelle in altri come onde.
luce
Comportamento ondulatorio:
Elettromagnetismo ed ottica in generale
Comportamento particellare:
Effetto fotoelettrico
Effetto Compton
materia
Comportamento particellare:
In tutti i casi di aggregati di più atomi
Comportamento ondulatorio:
Diffrazione di raggi di elettroni
13
La meccanica ondulatoria - L’
L’equazione di Schrö
Schrödinger
Propagazione delle onde elettro-magnetiche delle
onde sonore, delle vibrazioni di una corda
Onde e.m.
2f 2f 2f
1 2f
+
+
=
x 2 y2 z 2 c 2 t 2
f : E,B
densità di energia (E/V)
f2
(num. fotoni)/volume
probabilità di trovare un fotone
La meccanica ondulatoria - L’
L’equazione di Schrö
Schrödinger
Studio del moto degli elettroni attraverso le onde di De
Broglie ad essi associate
2 ' 2 ' 2 ' 1 2 '
+
+
=
x 2 y 2 z 2 v2 t2
Equazione dell’onda di De Broglie associata ad una
particella
2
' probabilità di trovare la particella in un
dato punto dello spazio in certo istante
Descrizione PROBABILISTICA del moto degli elettroni
14
Equazione di Schrödinger valida per gli
stati stazionari (indipendente dal tempo)
2 2 2 8 2 m
+
+
+ 2 ( E E p ) = 0
x 2 y 2 z 2
h
e2
Ep = r
La funzione deve:
• essere nulla all’infinito
• essere continua e ad un solo valore in ogni punto dello
spazio, insieme alle sue derivate
2
v = dV = 1
• soddisfare la condizione di normalizzazione
• soddisfare la condizione di ortogonalità v = m ndV = 0
L’atomo di idrogeno secondo la
meccanica quantistica
•E’ possibile risolvere in modo rigoroso l’eq. d’onda
per l’atomo di idrogeno
•Si determinano una serie di soluzioni (autofunzioni)
in corrispondenza di valori diversi dell’energia
(autovalori) ORBITALI atomici di H
•Lo stato dell’elettrone nell’atomo è descritto da uno
degli infiniti orbitali
15
Risoluzione dell’
dell’eq.
eq. di Schrö
Schrödinger per l’
l’atomo di idrogeno
2 2 2 8m e2 E + = 0 Integrando:
+
+
+
r h 2 x 2 y2 z2
Soluzioni accettabili solo per determinati valori dell’energia E
(autovalori):
En = 1 2 2me4 n = 1,2, 3,...,
Numero quantico principale
n 2 h2
coincide con l’espressione dedotta da Bohr!
Quantizzazione dell’
dell’energia (livelli energetici discreti):
• non da postulati arbitrariamente imposti (Bohr)
• conseguenza logica della natura dell’equazione e delle
condizioni che la funzione d’onda deve soddisfare per
avere un significato fisico valido
Numeri quantici
Le funzioni d’onda soluzioni dell’equazione di Schrödinger
(autofunzioni) sono funzioni matematiche complicate delle
coordinate dello spazio che contengono tre numeri quantici e
sono completamente definite dai loro valori
• Numero quantico principale n
• Numero quantico secondario o azimutale
l
• Numero quantico magnetico ml
pz = ml p = l (l + 1) h
2
h
2
n = 1,2,3,...,
l = 0,1,2,...,n 1
ml = l ,(l 1),...,0,+(l 1),+l
16
Numeri quantici
Il numero quantico n è in relazione con la
dimensione e l’energia dell’orbitale
Il numero quantico l è in relazione con la forma
degli orbitali atomici
Il numero quantico ml è in relazione con
l’orientazione relativa degli orbitali nello spazio
Numeri quantici e orbitali
Ogni autofunzione associata ad una definita terna di
valori di numeri quantici n, l, ml viene chiamata
ORBITALE.
Ogni orbitale corrisponde ad un determinato stato
quantico possibile dell’elettrone, la cui energia è:
1 2 2me4
En = 2
n
h2
Tipi di orbitali
l=0
l=1
l=2
l=3
Orbitale s
Orbitale p
Orbitale d
Orbitale f
17
Numeri quantici e orbitali
n = 1,2,3,...,
l = 0,1,2,...,n 1
ml = l ,(l 1),...,0,+(l 1),+l
n=1 l=0
n=2 l=0
l=1
ml = 0
ml = 0
ml = 0,±1
1 orbitale 1s
1 orbitale 2s
3 orbitali 2p
n = 3 l = 0 ml = 0
l = 1 ml = 0,±1
l = 2 ml = 0,±1,±2
1 orbitale 3s
3 orbitali 3p
5 orbitali 3d
n = 4 l = 0 ml = 0
l = 1 ml = 0,±1
l = 2 ml = 0,±1,±2
l = 3 ml = 0,±1,±2,±3
1 orbitale 4s
3 orbitali 4p
5 orbitali 4d
7 orbitali 4f
Numeri quantici e orbitali
18
Livelli energetici degli orbitali atomici dell’
dell’idrogeno
energia
Per l’atomo di idrogeno il valore dell’energia di un dato
orbitale dipende soltanto dal numero quantico principale n.
Orbitali caratterizzati dallo stesso livello energetico (2s-2p,
3s-3p-3d, ecc.) sono detti DEGENERI.
4s
3s
4p
3p
2s
2p
4d
3d
4f
Livelli energetici degli orbitali
atomici dell’idrogeno
1s
Rappresentazione degli orbitali atomici
ORBITA (meccanica classica)
definita da un’equazione matematica che ne determina
completamente il tipo e la rappresentazione geometrica nello
spazio
ORBITALE (meccanica quantistica)
definita da un’equazione matematica complicata
• la funzione d’onda non ha un significato fisico diretto
• 2 probabilità di trovare l’elettrone nel punto
considerato
19
Rappresentazione degli orbitali s dell’
dell’atomo di idrogeno
2 probabilità per unità di volume
2 è chiamata densità di probabilità
y
dr
r
x
z
2 · dV = 2 · 4r2dr = dP probabilità nel volume
infinitesimo di guscio sferico compreso fra r e r+dr
dP /dr = funzione di distribuzione della probabilità
20












