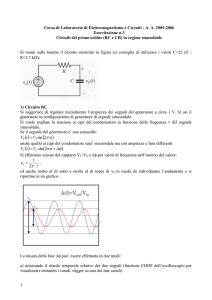
Circuito RC con d.d.p. sinusoidale
Un circuito RC-serie ha la seguente configurazione:
RG è la resistenza interna del generatore.
Misura dello sfasamento della tensione ai capi del condensatore rispetto alla tensione ai capi
della resistenza
Inviare all’ingresso del circuito una tensione sinusoidale. Collegare X e Y rispettivamente ai canali
1 e 2 dell’oscilloscopio facendo attenzione alla posizione dei terminali di terra. Scegliere X come
segnale di trigger e visualizzare i due canali contemporaneamente. Misurare il periodo T della
tensione sinusoidale e il ritardo temporale tr fra i due segnali per ricavare lo sfasamento θ:
θ=
tr
⋅ 360°
T
Determinare T e tr nel modo più preciso possibile e stimare l’errore di misura. Confrontare il valore
ottenuto per lo sfasamento con quello atteso secondo la formula:
tan θ =
1
ωτ
dove ω =
,
2π
e τ = RC .
T
1
Circuito RL con d.d.p. sinusoidale
Un circuito RL-serie ha la seguente configurazione:
RL e RG sono rispettivamente la resistenza dell’induttanza e del generatore.
Misura dello sfasamento della tensione ai capi dell’induttanza rispetto alla tensione ai capi
della resistenza
Procedere come nel caso del circuito RC. Utilizzare il valore ottenuto per lo sfasamento per dare
una stima del valore di L, sfruttando la relazione:
tan θ = ωτ
dove ω =
L
2π
eτ = .
T
R
Circuito RCL con d.d.p. sinusoidale
Un circuito RCL-serie ha la seguente configurazione:
2
RL e RG sono rispettivamente la resistenza dell’induttanza e del generatore.
L’ampiezza del segnale di corrente del circuito al variare della frequenza ω =
i=
2π
è:
T
V0
R 2 + (ωL −
1 2
)
ωC
dove V0 è l’ampiezza del segnale di tensione (VY nella figura).
La frequenza di risonanza è quella per cui:
1/ω0 C = ω0 L
di conseguenza per ω = ω0 la corrente i assume il suo valore massimo. Inoltre per questa frequenza
le tensioni Vx e Vy sono in fase fra loro.
La frequenza di risonanza è :
ω0 =
1
LC
(1) Misura della frequenza di risonanza
9 Montare il circuito in figura e impostare il generatore su una tensione sinusoidale. Collegare
Vx e Vy ai canali 1 e 2 dell’oscilloscopio e collegare i terminali di terra dei cavi coassiali
insieme col terminale di terra del generatore.
3
9 Impostare l’oscilloscopio in modalità X-Y. L’ellisse che si osserva sullo schermo è dovuta
allo sfasamento dei segnali Vx e Vy ; variando la frequenza del generatore si osserva una
variazione della forma dell’ellisse. Quando questa degenera in una retta, la frequenza
indicata dal generatore è quella di risonanza (N.B.: Agendo sui comandi di ampiezza dei
canali 1 e 2 fare in modo che la retta abbia un’inclinazione di circa 45°, per ottenere una
sensibilità maggiore).
9 Determinare l’errore su ω0 attraverso la minima variazione di frequenza del generatore che
provoca un significativo allargamento dell’ellisse.
(2) Determinazione dell’induttanza o della capacità
Dalla misura di ω0 è possibile determinare il valore dell’induttanza L se è noto il valore della
capacità:
L=
1
ω 02 C
oppure della capacità C se è noto il valore dell’induttanza:
C=
1
ω 02 L
Confrontare il valore di L così ottenuto, assumendo noto il valore di C, con la stima preliminare
fatta nella misura precedente.
Circuiti RC e RL con d.d.p. a onda quadra
La risoluzione del circuito RC (vedi figura a pag.1) porta alle seguenti espressioni per il potenziale
fra le armature del condensatore e ai capi della resistenza durante la fase di carica del condensatore:
−t
Vcond . (t ) = V0 1 − e RC e
−t
Vresist . (t ) = V0 ⋅ e RC
dove V0 è la tensione costante che il generatore raggiunge “istantaneamente” partendo da 0 V.
4
Durante la fase di scarica la tensione del generatore torna istantaneamente a zero: le espressioni dei
potenziali sono:
Vcond . (t ) = V0 ⋅ e
−t
RC
e
Vresist . (t ) = −V0 ⋅ e
−t
RC
.
Se si applica un segnale a onda quadra fra 0 e V0, per visualizzare le fasi di carica e scarica del
condensatore è necessario che il suo periodo T sia maggiore di τ = RC (costante di tempo del
circuito) ; la frequenza f del segnale va dunque scelta in modo che sia:
f < 1/τ
Sia misurando la d.d.p. ai capi della resistenza, come in figura a pag.1, sia misurando quella ai capi
del condensatore (si scambia R con C) è possibile ricavare il valore di τ attraverso la misura del
tempo di dimezzamento. Infatti nelle regioni in cui il potenziale ha un andamento esponenziale
decrescente si può scrivere:
V
t
t
V (t ) = V0 ⋅ exp −
→ 0 = V0 exp − 1 / 2 ,
2
RC
RC
da cui si ricava t1 / 2 = τ ⋅ ln 2 = RC ⋅ ln 2
La misura di τ consente di ricavare il valore di C nel caso di condensatore di valore incognito:
C=
τ
R
Misura del tempo di dimezzamento per valutare τ
9 Montare il circuito e impostare il generatore su segnale a onda quadra ponendosi nelle
condizioni f < 1/τ Nota: collegare il generatore di segnale al circuito tramite cavo coassiale
prelevando il segnale dall’uscita a 50 Ω per ridurre il contributo di questa resistenza interna
del generatore alla costante τ del circuito RC.
5
9 Impostare il canale dell’oscilloscopio su DC e regolare opportunamente la base dei tempi in
modo da visualizzare la zona con andamento esponenziale decrescente su tutto lo schermo
dell’oscilloscopio (usare anche il comando LEVEL)
9 Attraverso il comando Y-POS allineare la regione di andamento asintotico con una divisione
dello schermo e misurare la caduta di potenziale totale. Determinare quindi l’intervallo di
tempo per il quale il potenziale si riduce della metà spostando con il comando X-POS la
curva in modo che V0/2 coincida con l’intersezione della curva con una divisione verticale
dello schermo. In questo modo t1/2 è dato dalla distanza fra questa divisione e l’inizio della
curva ( V=V0 ) Nota: attraverso la regolazione dell’ampiezza del segnale in ingresso e della
sensibilità dell’oscilloscopio fare in modo che la curva abbia una pendenza non molto
elevata così da ridurre l’errore sulla determinazione di V0/2.
9 Determinare l’errore su t1/2 attraverso la minima traslazione sull’asse X che sposta
significativamente da V0/2 il punto di intersezione suddetto. Determinare quindi τ attraverso
la relazione t1 / 2 = τ ⋅ ln 2
9 Ripetere la misura scambiando R con C e misurando la ddp ai capi di quest’ultimo.
Misura di induttanza incognita in un circuito RL
Montare il circuito RL come nella figura a pag. 2 (misurare prima con il multimetro la resistenza
dell’induttanza).
Per effetto del gradino di tensione fra 0 e V0 inviato dal generatore al circuito RL, la tensione ai capi
della resistenza aumenta da 0 a V0 secondo la legge:
Vres = V0 (1 − e
−
R
t
L
)
Quando il segnale del generatore passa istantaneamente da V0 a 0 si ha invece:
Vres = V0 ⋅ e
−
R
t
L
La costante di tempo della funzione esponenziale è:
6
τ=
L
R
Determinare il tempo di dimezzamento in modo analogo a quanto fatto per il circuito RC
scegliendo una frequenza f opportuna, tenendo conto che deve valere la relazione:
f < 1/τ
Noto τ , ricavare nuovamente il valore di L e confrontarlo con le precedenti misure:
L =τ ⋅R
7