Dispensa 1

Istituto Statale d’Arte “ Max Fabiani ” di Gorizia
ANNO SCOLASTICO 2009 - 2010
CLASSE : 1^ e 2^
SEZIONE : A - B
DISEGNO GEOMETRICO
DISPENSA N° 1
GEOMETRIA - DEFINIZIONI
GLOSSARIO
GEOMETRIA
= La G. è quella parte della scienza che studia la forma e l’estensione del corpi .
I suoi enti fondamentali sono : il PUNTO, la LINEA e la SUPERFICIE
Le dimensioni di un corpo sono : la LUNGHEZZA, la LARGHEZZA e la PROFONDITA’
Il PUNTO non ha dimensioni, un granellino di sabbia può darne solo un’idea .
I PUNTI si indicano con le LETTERE maiuscole .
Un insieme di PUNTI costituiscono una FIGURA .
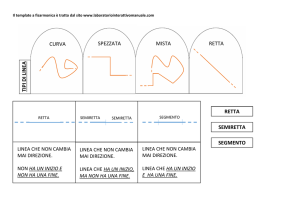
LINEA e RETTA = Dicesi LINEA la traccia lasciata da un PUNTO in moto .
La LINEA ha infiniti PUNTI, ma ha una sola dimensione : la LUNGHEZZA
La RETTA è la LINEA tracciata da un PUNTO che si muove sempre nella stessa
direzione .
Una RETTA si indica con una sola lettera minuscola o con due lettere maiuscole poste
su due suoi punti qualsiasi .
La RETTA è illimitata da ambo le parti .
SUPERFICIE
= Dicesi SUPERFICIE ciò che limita un CORPO e ne determina la forma .
Dobbiamo immaginare la SUPERFICIE come una pellicola sottilissima (priva di
spessore) che delimita da ogni parte il CORPO .
Su di una SUPERFICIE giacciono infiniti PUNTI ed infinite LINEE : queste possono
essere RETTE, SPEZZATE, CURVE e MISTE .
Per comprendere cosa sia il PIANO immaginiamo la SUPERFICIE di un tavolo, della
lavagna o del foglio di carta e pensiamo di estenderle da ogni parte indefinitamente .
Un PIANO è infinitamente LUNGO ed infinitamente LARGO, ma non ha SPESSORE .
Il PIANO si indica con una lettera minuscola dell’ALFABETO GRECO .
DISEGNARE
= l’azione del DISEGNARE viene (più correttamente) indicata come : RAPPRESENTARE
TRACCIANDO (con matite, compassi, ecc.) una RETTA, un PIANO, ma in effetti
disegneremo soltanto una parte di essi, per l’impossibilità di giungere ... all’infinito .
Lo SPAZIO è l’insieme di tutti i PUNTI, di tutte le LINEE e di tutte le SUPERFICI è cioè
l’insieme di tutti i CORPI .
1/20
GEOMETRIA PIANA
RETTE - SEMIRETTE - SEGMENTI
L’idea della RETTA ci viene data da un filo sottilissimo ben teso .
Per un PUNTO passano infinite RETTE .
Per due PUNTI passa una sola RETTA .
Un PUNTO divide una RETTA in due SEMIRETTE, le quali hanno un PUNTO in comune “ O “ detto anche
ORIGINE o LIMITE .
La SEMIRETTA è indefinita da una parte sola .
Due PUNTI determinano su di una RETTA un SEGMENTO e due SEMIRETTE .
I due PUNTI diconsi ESTREMI del SEGMENTO e sono le ORIGINI delle due SEMIRETTE .
Pertanto si definisce che il SEGMENTO è quella parte di RETTA delimitata fra due PUNTI i quali diconsi
ESTREMI del SEGMENTO .
SEGMENTI CONSECUTIVI : hanno un estremo in comune .
B
A
C
SEGMENTI ADIACENTI : sono consecutivi se giacciono sulla stessa RETTA, ma gli estremi giacciono
da parti opposte rispetto all’estremo comune .
B
A
C
SEGMENTI SOVRAPPOSTI : non sono adiacenti perchè A e C non giacciono da parti opposte rispetto a B
I due SEGMENTI si dicono SOVRAPPOSTI PARZIALMENTE
C
A
B
Aspetti finali sui SEGMENTI : uguaglianza, somma, sottrazione, multipli, ecc. .
PIANI - SEMIPIANI
come detto il PIANO è una SUPERFICIE “ speciale “ . Il PIANO ha infiniti PUNTI ed infinite RETTE .
Una RETTA divide il PIANO in due SMIPIANI .... in tal caso la RETTA dicesi LIMITE o FRONTIERA dei due
SEMIPIANI .
2/20
Una RETTA che ha in comune con un PIANO due PUNTI, giace tutta sul PIANO, cioè appartiene al PIANO
Per un PUNTO dello spazio passano infiniti PIANI .
Per due PUNTI dello spazio ed anche per una RETTA dello spazio, passano infiniti PIANI
Perchè un PIANO sia individuato è necessario tener presente che esso è determinato :
1°) da tre PUNTI non allineati sulla stessa RETTA e, logicamente :
2°) da una RETTA ed un PUNTO fuori di essa .
3°) da due RETTE che si intersecano (o da due RETTE parallele) .
ANGOLI
Se due RETTE di un PIANO s’intersecano dividono il PIANO in quattro regioni, dette REGIONI ANGOLARI
od ANGOLI .
A
D
o
B
C
Perciò :
si dice ANGOLO la REGIONE di PIANO compresa fra due SEMIRETTE aventi la medesima ORIGINE .
Le due SEMIRETTE si dicono LATI e la loro ORIGINE comune dicesi VERTICE dell’ANGOLO .
un ANGOLO si può indicare con tre lettere maiuscole, due poste lungo i LATI ed una al VERTICE .
Quella al VERTICE si legge per seconda e, scrivendo, le si pone il segno “ /\ “ .
A volte l’ANGOLO si indica o meglio si legge con la sola lettera maiuscola posta al vertice od una lettera
minuscola messa all’interno .
A
B
vertice
lato
a
M
C
lato
Un ANGOLO si dice CONVESSO se i prolungamenti dei lati (al di là del VERTICE) risultano esterni
all’ANGOLO - ovvero i prolungamenti dei LATI non l’attraversano .....
Si dice CONCAVO se i prolungamenti risultano interni all’ANGOLO - ovvero se gli stessi prolungamenti
attraversano i LATI .
3/20
A
A
B
B
C
ANGOLO CONVESSO
C
ANGOLO CONCAVO
Un ANGOLO si dice PIATTO se i suoi LATI sono SEMIRETTE opposte .
A
O
B
Un ANGOLO GIRO è formato da due ANGOLI PIATTI .
ANGOLI CONSECUTIVI - ANGOLI ADIACENTI
Due ANGOLI CONVESSI si dicono CONSECUTIVI se hanno il VERTICE ed un LATO in COMUNE e gli
altri due LATI sono disposti da parti opposte rispetto al LATO COMUNE .
Due ANGOLI si dicono ADIACENTI se sono CONSECUTIVI ed i LATI non COMUNI giacciono sulla stessa
RETTA .
D
A
C
B
A
D
ANGOLI CONSECUTIVI
B
ANGOLI ADIACENTI
4/20
C
CONFRONTO DI ANGOLI
Tutti gli ANGOLI PIATTI sono uguali ....
Se un ANGOLO è uguale ad un secondo ed il secondo è uguale ad un terzo, il primo è uguale al terzo
(proprietà transitiva) .
La misura, il confronto e le operazioni sugli AMGOLI si possono fare servendosi del GONIOMETRO o
RAPPORTATORE . Esso in effetti è un ANGOLO PIATTO il cui arco è diviso in 180 parti detti GRADI
SESSAGESIMALI .
Per misure di maggior precisione, ogni GRADO si divide in 60 MINUTI PRIMI ed ogni PRIMO in 60 MINUTI
SECONDI .
Per misurare un ANGOLO con il RAPPORTATORE si pone il centro O di questo sul VERTICE dell’ANGOLO
ed uno degli SPIGOLI dello strumento su uno dei LATI .
Il numero sul quale l’altro LATO dell’ANGOLO incontra il SEMICERCHIO graduato dà la misura richiesta .
SOMMA e DIFFERENZA di ANGOLI - MULTIPLI e SOTTOMULTIPLI
Per ADDIZIONARE due ANGOLI si rendono CONSECUTIVI; l’ANGOLO formato dai due LATI non COMUNI
è la loro SOMMA .
Per SOTTRARRE due ANGOLI si sovrappone al maggiore in modo che abbiano il VERTICE ed un LATO
COMUNE . La parte rimanente del maggiore si dice DIFFERENZA fra i due ANGOLI .
La DIFFERENZA di due ANGOLI uguali è NULLA .
Si dice multiplo di un ANGOLO un altro ANGOLO eguale alla somma di tanti ANGOLI uguali al primo .
Viceversa l’ANGOLO MINORE, in tal caso, è un SOTTOMULTIPLO del maggiore .
Due ANGOLI si dicono SUPPLEMENTARI se la loro somma è un ANGOLO PIATTO .
Due ANGOLI ADIACENTI sono sempre SUPPLEMENTARI .
N.B. : se due ANGOLI sono SUPPLEMENTARI non è VERO che debbano essere per forza ADIACENTI,
poichè uno di essi potrebbe essere disegnato a ROMA e l’altro a MILANO ..... e la loro somma risultare un
ANGOLO PIATTO .
ANGOLI SUPPLEMENTARI di ANGOLI uguali sono uguali .
ANGOLI ADIACENTI di uno stesso ANGOLO sono uguali .
ANGOLI ADIACENTI di ANGOLI uguali sono uguali .
Due ANGOLI si dicono OPPOSTI al VERTICE se i LATI dell’uno sono i prolungamenti dei LATI dell’altro .
Due ANGOLI OPPOSTI al VERTICE sono uguali .
Si dice BISETTRICE di un ANGOLO la SEMIRETTA che divide l’ANGOLO in due parti uguali .
5/20
RETTE PERPENDICOLARI e RETTE PARALLELE
Due RETTE intersecandosi formano quattro ANGOLI a due a due OPPOSTI al VERTICE e perciò a due a
due UGUALI .
Due RETTE si dicono PERPENDICOLARI se incontrandosi formano tutti e quattro gli ANGOLI uguali .
Gli ANGOLI formati in tal caso si dicono RETTI .
L’ANGOLO RETTO è la metà dell’ANGOLO PIATTO .
Cioè l’ANGOLO PIATTO è uguale alla somma di due ANGOLI RETTI .
L’ANGOLO GIRO, che vale due ANGOLI PIATTI, è uguale perciò a quattro ANGOLI RETTI .
Si dice ANGOLO ACUTO l’ANGOLO minore di un RETTO .
Si dice ANGOLO OTTUSO l’ANGOLO maggiore di un RETTO .
Due ANGOLI si dicono COMPLEMENTARI se la loro somma è un ANGOLO RETTO .
ANGOLI COMPLEMENTARI di uno stesso ANGOLO sono uguali .
ANGOLI COMPLEMENTARI di ANGOLI uguali sono uguali .
REGOLE
Da un PUNTO non si può condurre che una ed una sola PERPENDICOLARE ad una data RETTA :
sia se il PUNTO è sulla RETTA o fuori della RETTA .
Dicesi distanza di un PUNTO da una RETTA il SEGMENTO di PERPENDICOLARE che va dal PUNTO alla
RETTA .
Da un PUNTO fuori di una RETTA si può condurre un solo SEGMENTO PERPENDICOLARE alla RETTA .
Ogni altro SEGMENTO condotto dal PUNTO alla RETTA dicesi OBLIQUO .
Lo strumento che serve a condurre delle PERPENDICOLARI ad una RETTA è la SQUADRETTA .
RETTE PARALLELE
Se due RETTE qualsiasi di un PIANO vengono tagliate da una terza RETTA, detta TRASVERSALE, la quale
forma otto angoli che a coppie prendono dei nomi che gli ALLIEVI hanno l’obbligo di imparare ad individuare
ed a nominare molto bene : ANGOLI INTERNI, ANGOLI ESTERNI, ANGOLI CORRISPON_ DENTI, ANGOLI
CONIUGATI INTERNI e ANGOLI CONIUGATI ESTERNI .
Dure RETTE distinte di un PIANO possono presentarsi soltanto nelle due posizioni :
RETTE che si INTERSECANO - ovvero avere un PUNTO vicino o lontano in COMUNE ....
RETTE che non si INTERSECANO - ovvero non avere un PUNTO vicino o lontano in COMUNE ....
Due RETTE si dicono PARALLELE se non hanno alcun PUNTO in COMUNE .
Si dice DISTANZA fra due RETTE PARALLELE il SEGMENTO di PERPENDICOLARE condotto da un
PUNTO qualunque di una RETTA all’altra .
6/20
Le distanze fra ogni PUNTO di una RETTA ed una PARALLELA a questa sono sempre uguali .
REGOLE
Per stabilire se due RETTE sono PARALLELE si può ricorrere alla seguente regola di grandissima
importanza .
Due RETTE sono PARALLELE se con una trasversale formano :
1° ANGOLI alterni interni od alterni esterni uguali ;
2° ANGOLI corrispondenti uguali ;
3° ANGOLI CONIUGATI interni o CONIUGATI esterni SUPPLEMENTARI .
Questa REGOLA va imparata molto bene e verificata su un vostro disegno con il GONIOMETRO .
POSTULATI
Della PARALLELA unica : per un PUNTO fuori di una RETTA passa una ed una sola PARALLELA
alla RETTA
N.B. : questa regola rassomiglia a quella della PERPENDICOLARE unica, già trattata .
In effetti quella è vera perché è vera questa e viceversa .
POLIGONI
Si dice POLIGONO la parte di PIANO limitata da una SUPERFICIE chiusa .
Si dicono LATI del POLIGONO i LATI della SPEZZATA , VERTICI del POLIGONO gli ESTREMI dei LATI .
ANGOLI INTERNI o semplicemente ANGOLI del POLIGONO gli ANGOLI formati da due LATI
CONSECUTIVI .
Un ANGOLO ESTERNO di un POLIGONO è quello formato da un LATO e dal “ prolungamento “ del LATO
CONSECUTIVO .
Un POLIGONO si dice CONVESSO se prolungando i LATI da ambo le parti, nessun prolungamento taglia il
POLIGONO, altrimenti il POLIGONO si dice CONCAVO .
Si dice DIAGONALE di un POLIGONO il SEGMENTO che congiunge due VERTICI non CONSECUTIVI di
esso .
Il PERIMETRO di un POLIGONO è la somma dei LATI .
Nome del POLIGONO in base al n° dei LATI : triangolo, quadrilatero o quadrangolo, pentagono, esagono,
ettagono, ottagono, ennagono, decagono, endecagono, dodecagono .....
e poi POLIGONO di 13 LATI, 14 LATI, ecc. ( eccetto quello di 15 LATI che viene chiamato
PENTEDECAGONO e quello di 20 detto ICOSAGONO ) .
Un POLIGONO si dice EQUILATERO se ha tutti i LATI uguali .
Un POLIGONO si dice EQUIANGOLO se ha tutti gli ANGOLI uguali .
Un POLIGONO si dice REGOLARE se ha tutti i LATI e gli ANGOLI uguali .
7/20
TRIANGOLO
Il TRIANGOLO è il POLIGONO limitato da TRE LATI .
Esso ha logicamente tre ANGOLI ed è sempre CONVESSO .
In ogni TRIANGOLO la somma di tutti gli ANGOLI INTERNI è un ANGOLO PIATTO - cioè due RETTI .
Tipi di TRIANGOLI rispetto ai LATI : - equilatero se ha i LATI tutti uguali fra di loro ;
- isoscele se ha due LATI eguali fra loro detti LATI OBLIQUI
ed il terzo disuguale detto BASE ;
- scaleno se ha i LATI tutti disuguali .
Tipi di TRIANGOLI rispetto agli ANGOLI : - acutangolo se ha gli ANGOLI tutti ACUTI ;
- rettangolo se ha un ANGOLO RETTO (e gli altri
due necessariamente ACUTI e COMPLEMENTARI)
- ottusangolo se ha un ANGOLO OTTUSO (e gli altri due
necessariamente ACUTI, ma non COMPLEMENTARI) .
Il TRIANGOLO EQUILATERO è anche EQUIANGOLO .
Nel TRIANGOLO ISOSCELE gli ANGOLI alla BASE sono uguali .
ALTEZZE - MEDIANE - BISETTRICI
Si dice ALTEZZA di un TRIANGOLO il SEGMENTO di PERPENDICOLARE condotto da un VERTICE sul
LATO OPPOSTO ( o sul prolungamento di questo ) .
In ogni TRIANGOLO ogni LATO può fare da BASE - perciò ogni TRIANGOLO ha tre ALTEZZE il PUNTO COMUNE “ O “ viene chiamato ORTOCENTRO .
Si dice MEDIANA di un TRIANGOLO il SEGMENTO che unisce un VERTICE con il PUNTO MEDIO
del LATO OPPOSTO - perciò ogni TRIANGOLO ha tre MEDIANE - il PUNTO COMUNE “ G “ viene
chiamato BARICENTRO o CENTRO di GRAVITA’ del TRIANGOLO .
Si dice BISETTRICE di un TRIANGOLO il SEGMENTO che va da un VERTICE al LATO OPPOSTO
dividendo per META’ l’ANGOLO - perciò ogni TRIANGOLO ha tre BISETTRICI - il PUNTO COMUNE
“ I “ viene chiamato INCENTRO o CENTRO del cerchio inscritto nel TRIANGOLO .
N.B. : nel TRIANGOLO ISOSCELE l’ALTEZZA, la MEDIANA e la BISETTRICE, relative alla cosiddetta
BASE : coincidono .
CRITERI D’EGUAGLIANZA DEI TRIANGOLI
Due TRIANGOLI sono eguali se sovrapponendo l’uno all’altro, gli ANGOLI ed i LATI dell’uno coincidono con
quelli dell’altro .
In particolare :
1° - due TRIANGOLI sono uguali se hanno due LATI e l’ANGOLO compreso rispettivamente uguali .
2° - due TRIANGOLI sono uguali se hanno un LATO ed i due ANGOLI ADIACENTI rispettivamente uguali .
3° - due TRIANGOLI sono uguali se tutti e tre i LATI dell’uno sono eguali rispettivamente a quelli dell’altro .
8/20
LUOGHI GEOMETRICI
Si dice luogo geometrico una figura i cui punti godono di una certa proprietà geometrica e solo i suoi punti
hanno quella proprietà .
Per esempio : la circonferenza , infatti tutti i suoi punti hanno la proprietà di avere sempre la stessa
distanza dal centro (raggio) . Ne parleremo in seguito ....
Altri luoghi geometrici importanti sono : l’asse di un segmento e la bisettrice di un angolo .
L’asse di un segmento, che è la perpendicolare passante per il punto medio del segmento, è il luogo
geometrico dei punti equidistanti dagli estremi del segmento .
Anche la bisettrice di un angolo ha tutti i suoi punti equidistanti dai lati dell’angolo .
QUADRILATERI
Il QUADRILATERO è un POLIGONO di quattro LATI, quattro VERTICI, quattro ANGOLI e due DIAGONALI.
Tanto più il Q. tende a diventare regolare nei suoi elementi, tanto più cambiano le sue caratteristiche ed
assume vari nomi .
TRAPEZIO
Dicesi T. il Q. che ha due LATI OPPOSTI PARALLELI .
I due LATI PARALLELI diconsi BASI del T. e gli altri due LATI non PARALLELI diconsi LATI OBLIQUI .
Dicesi ALTEZZA di un T. la distanza fra le due BASI .
Un T. si dice SCALENO se ha i LATI OBLIQUI diseguali .
Un T. si dice ISOSCELE se ha i LATI OBLIQUI uguali .
Un T. si dice RETTANGOLO se uno dei LATI non PARALLELO diventa PERPENDICOLARE alle BASI .
PARALLELOGRAMMA
Dicesi P. un Q. avente i LATI OPPOSTI PRALLELI .
Il P. ha le seguenti proprietà :
- ogni diagonale lo divide in due triangoli uguali ;
- i lati opposti sono uguali ;
- gli angoli opposti sono uguali ;
- le diagonali di tagliano per metà .
9/20
PARALLELOGRAMMI PARTICOLARI
Correggendo alcune sue irregolarità, dà luogo a tre figure particolari :
- il P. RETTANGOLO
- il P. ROMBO
- il P. QUADRATO
:dicesi R. il parallelogramma che ha tutti gli angoli uguali (quindi retti) ;
: dicesi R. il parallelogramma che ha tutti i lati uguali (ed in particolare le diagonali
sono perpendicolari tra loro e sono anche bisettrici degli angoli ai vertici - ved. T.
ISOSCELE) ;
: dicesi Q. il parallelogramma che ha tutti gli angoli uguali (quindi retti) e
tutti i lati uguali .
Il Q. perciò discende dal parallelogramma e più direttamente dal rettangolo e dal
rombo insieme. Non meraviglia quindi se ha tutte le proprietà dei suoi ... antenati .
Il Q. è anche come : QUADRILATERO REGOLARE .
CIRCONFERENZA e CERCHIO
Si dice Crf. (CIRCONFERENZA). una linea piana chiusa, i cui punti sono tutti equidistanti da uno stesso
punto del piano, detto CENTRO .
La distanza di un punto qualunque dal centro è detta RAGGIO
La Crf. è il luogo geometrico dei punti del piano tutti equidistanti dal centro .
Lo strumento che si usa per tracciare le Crf. è il compasso .
Si dice CORDA un segmento di retta che unisce due punti della Crf. .
Il DIAMETRO è la CORDA passante per il CENTRO .
La CORDA maggiore di una Crf. è il DIAMETRO .
Dicesi ARCO una parte di Crf. compresa fra due punti .
Ogni DIAMETRO divide la Crf. in due ARCHI eguali detti SEMICIRCONFERENZE .
Dicesi CERCHIO la parte di piano limitata dalla CIRCONFERENZA .
N.B. : quindi mentre la Crf. è una linea, il CERCHIO è una superficie .
L’una ha una lunghezza e l’altra ha un’area ; l’una sarà misurata in metri lineari (ml.) , l’altro in metri
quadrati (mq.) .
Un DIAMETRO divide un CERCHIO in due SEMICERCHI (uguali) .
Due Crf. o due CERCHI aventi raggi uguali sono uguali, infatti facile è sovrapporli .
La parte di CERCHIO racchiusa fra una CORDA e l’ARCO che la sottende dicesi SEGMENTO CIRCOLARE
AD UNA BASE . Invece la parte racchiusa fra due CORDE PARALLELE è detta SEGMENTO CIRCOLARE A
DUE BASI .
Il SETTORE CIRCOLARE è la parte di CERCHIO compresa fra due raggi e l’arco sotteso .
10/20
POSIZIONI RELATIVE DI RETTE E CIRCONFERENZE E DI CIRCONFERENZE FRA DI LORO
Una RETTA si dice SECANTE se ha due punti in comune con la Crf. . La sua distanza dal centro è minore
del raggio .
Una RETTA si dice TANGENTE se ha un solo punto in comune con la Crf. . La sua distanza dal centro è
uguale al raggio .
Ricordarsi che la TANGENTE è sempre PERPENDICOLARE al RAGGIO passante per il punto di
TANGENZA .
Una RETTA si dice ESTERNA ad una Crf. se non ha alcun punto in comune con essa. La sua distanza dal
centro è sempre maggiore del raggio .
CONVINZIONI
- per tre punti non allineati passa una sola Crf. . Perciò, se due Crf. hanno tre punti in comune :
COINCIDONO ;
- due Crf., per essere distinte, non possono avere più di due punti in comune. Cosicché. anch’esse, se
hanno due punti di intersezione, si dicono SECANTI, se hanno un punto di contatto si dicono TANGENTI
(internamente od esternamente) ;
- e se non hanno alcun punto in comune si dicono ESTERNE ( o INTERNE) . Per le Crf. INTERNE
l’una all’altra c’è un caso particolare e si ha quando le due Crf. hanno lo stesso centro, cioè sono
CONCENTRICHE .
La parte di cerchio compresa fra la Crf. maggiore e quella minore dicesi : CORONA CIRCOLARE .
Ogni ANGOLO inscritto in mezza Crf. (SEMICIRCONFERENZA) è RETTO .....
Infatti l’ANGOLO al centro relativo è PIATTO ....
POLIGONI INSCRITTI e CIRCOSCRITTI
Un P. si dice INSCRITTO in una Crf. quando i suoi VERTICI sono punti della Crf. .
Nel P. INSCRITTO, perciò, i lati sono CORDE della Crf., la quale si dirà CIRCOSCRITTA al P. .
Un P. si dice CIRCOSCRITTO ad una Crf. se i suoi LATI sono TANGENTI alla Crf. .
In tal caso la Crf. si dice INSCRITTA nel P. .
Ricordando che :
un POLIGONO si dice regolare se ha lati ed angoli uguali, cioè se è EQUILATERO e EQUIANGOLO
contemporaneamente .
FIGURE INSCRITTIBILI MA NON CIRCOSCRITTIBILI E VICEVERSA
Come noto alcune figure possono essere INSCRITTE ma non CIRCOSCRITTE ad una Crf. , mentre altre
si possono CIRCOSCRIVERE ma non INSCRIVERE .
11/20
FIGURE INSCRITTIBILI E CIRCOSCRITTIBILI CONTEMPORANEAMENTE
Ogni POLIGONO regolare è sempre INSCRITTIBILE e CIRCOSCRITTIBILE ad una Crf.
I due centri, quello della Crf. INSCRITTA e quello della CIRCOSCRITTA, coincidono in un unico punto detto
CENTRO DEL POLIGONO .
C’è solo un P. che, anche se irregolare, è sempre INSCRITTIBILE e CIRCOSCRITTIBILE, questo P. è il
TRIANGOLO .
Se il T. è equilatero il centro delle due Crf., logicamente è unico, ma se il T. non è regolare i centri sono due
punti distinti .
Il centro della Crf. CIRCOSCRITTA al T. si dice CIRCUMCENTRO ed è il punto d’incontro degli ASSI dei
LATI .
ll centro della Crf. INSCRITTA nel T. si dice INCENTRO ed è l punto d’incontro delle BISETTRICI degli
ANGOLI .
EQUIVALENZE DI FIGURE PIANE
Come già descritto, due figure sono uguali quando, con la sovrapposizione si possono fare coincidere in ogni
loro parte .
Pertanto, due figure eguali hanno eguali superficie od estensione .
Due figure possono invece avere eguale estensione e non essere sovrapponibili, cioè non essere eguali .
Per esempio : un triangolo isoscele ed un rettangolo non sono sovrapponibili, ma potrebbero avere
eguale superficie (e si badi che sono costituiti da triangoli uguali) .
Quando due figure hanno EGUAGLIANZA di estensione si dice che sono EQUIESTESE, od
EQUISCOMPONIBILI od EQUIVALENTI .
CASI PARTICOLARI DI EQUIVALENZA
1) Due parallelogrammi aventi eguali basi ed eguali altezze sono equivalenti .
2) Un parallelogramma è equivalente ad un rettangolo che ha egual base ed eguale altezza .
3) Un rombo è equivalente alla metà di un rettangolo che ha le dimensioni eguali alle diagonali del rombo .
4) Un triangolo è equivalente alla metà di un parallelogramma avente egual base ed eguale altezza .
5) Un trapezio è equivalente ad un triangolo avente eguale altezza e per base la somma delle basi .
6) Un cerchio è equivalente ad un triangolo avente per base la Crf. e per altezza il raggio .
12/20
PITAGORA
Il quadrato costruito sull’ipotenusa di un triangolo rettangolo è equivalente alla somma dei quadrati costruiti
sui cateti .
AREA DELLA SUPERFICIE DEI POLIGONI REGOLARI
Ricordando che il P. regolare è equivalente ad un TRIANGOLO che ha per base il perimetro del P. e per
altezza l’APOTEMA, si può subito dare la seguente regola :
REGOLA : l’area della superficie di un P. regolare si ottiene moltiplicando la lunghezza del perimetro
per quella dell’apotema e dividendo il prodotto per 2 .
ovvero
S = Perimetro * Apotema / 2
da cui ne deriva che
P=2*S/A
ed anche
A=2*S/P
cioè l’APOTEMA vale quindi : 2 * SUPERFICIE / Perimetro
L’inconveniente grave quando si tratta di POLIGONI è quello di non poter conoscere la misura
dell’APOTEMA .
Nei P. regolari esistono, per fortuna, delle relazioni costanti dette “ RAPPORTI FISSI “ che permettono di
trovare la misura dell’APOTEMA data quella del LATO e viceversa (Ved. Tabelle ...) .
AREA DELLA SUPERFICIE DEL CERCHIO - CORONA CIRCOLARE - SETTORE CIRCOLARE E
SEGMENTO CIRCOLARE
Potendo considerare il CERCHIO come un P. regolare il cui PERIMETRO è la Crf. ed il cui APOTEMA è il
RAGGIO .
REGOLA :
L’area della SUPERFICIE del CERCHIO si ottiene moltiplicando la LUNGHEZZA della Crf. per il RAGGIO e
dividendo il prodotto per 2 .
L’area della SUPERFICIE di un CERCHIO si ottiene moltiplicando il quadrato del RAGGIO per 3,14 (cioè per
).
Conoscendo l’area del CERCHIO, per avere la lunghezza del RAGGIO si divide l’area per
radice quadrata del quoziente .
Cioè :
R= S/
e si estrae la
REGOLA :
L’area della SUPERFICIE di una CORONA CIRCOLARE è data dalla differenza del CERCHIO maggiore e
l’area del CERCHIO minore .
Ne deriva :
2
2
Scc =
* (R - r )
Considerando che un SETTORE CIRCOLARE è come un TRIANGOLO ISOSCELE avente per base l’ARCO
e per altezza il RAGGIO, si ha subito :
13/20
Ssc =
* r
2
*
/ 360°
da cui :
r=
360° * S /
*
ed anche :
= 360° * S /
* r
2
Se si volesse l’area del SEGMENTO CIRCOLARE ad una base, e non contenente il CENTRO, si potrebbe
trovare l’area della SUPERFICIE del SEGMENTO minore e poi sottrarla all’area del CERCHIO .
Oppure si potrebbe calcolare l’area del SETTORE con l’angolo CONCAVO ed a questa aggiungere, anziché
togliere, l’area del TRIANGOLO ISOSCELE .
14/20
GEOMETRIA SOLIDA
Finora tutte le figure studiate le abbiamo immaginate su di un unico piano .
La GEOMETRIA SOLIDA o STEREOMETRIA invece studia le figure comunque disposte nello spazio e tali
che in un sol piano non possono essere contenute .
RETTE E PIANI NELLO SPAZIO
RICORDANDO :
Nello spazio perché un PIANO sia ben determinato bisogna che sia individuato da una di queste tre
condizioni :
1^) da tre punti non allineati, cioè non posti sulla stessa retta ;
2^) da una retta e da un punto fuori di essa ;
3^) da due rette che s’intersecano (o da due rette parallele) .
Lo spazio che da un PIANO viene diviso in due SEMISPAZI, contiene infiniti PIANI e quindi infinite RETTE ed
infiniti PUNTI .
Una RETTA fuori di un PIANO può avere un sol PUNTO in comune con esso . Questo PUNTO in comune
dicesi PUNTO d’INTERSEZIONE o d’INTERSECAZIONE .
Se una RETTA ha in comune due PUNTI con un piano giace tutta sul PIANO, cioè appartiene al PIANO .
Due RETTE nello spazio possono essere :
COMPLANARI se stanno in uno stesso PIANO (Esempio : due rette che s’intersecano o che sono parallele)
SGHEMBE od ANAPLANE se non possono giacere in uno stesso PIANO e perciò non si incontrano mai .
A loro volta due PIANI distinti o si INTERSECANO o sono PARALLELI .
I PIANI non possono essere SGHEMBI ......
Due PIANI distinti non possono avere che una sola RETTA comune detta RETTA di INTERSECAZIONE o di
INTERSEZIONE .
RETTE E PIANI PERPENDICOLARI
Se una RETTA, incontrando un PIANO, è perpendicolare a tutte le RETTE del PIANO che passano per il suo
PUNTO di INTERSEZIONE di dice che è PERPENDICOLARE al PIANO .
Non è necessario né possibile stabilire che una RETTA sia PERPENDICOLARE a tutte le RETTE del PIANO
passanti per la sua INTERSEZIONE per concludere che la RETTA è PERPENDICOLARE al PIANO
Basta il seguente criterio :
se una RETTA è PERPENDICOLARE a due RETTE di un PIANO è PERPENDICOLARE al PIANO .
Necessariamente queste due RETTE debbono passare per il PUNTO d’INTERSEZIONE .
15/20
Si dice distanza di un PUNTO dal un PIANO il SEGMENTO di PERPENDICOLARE condotto dal PUNTO al
PIANO .
Si dice ANGOLO di una RETTA con un PIANO l’ANGOLO che la RETTA forma con la sua PROIEZIONE sul
PIANO .
Questo ANGOLO è il minore di tutti gli ANGOLI che la RETTA forma con le RETTE del PIANO passanti per il
PUINTO d’INTERSEZIONE .
RETTE E PIANI PARALLELI
Perché una RETTA, ESTERNA ad un PIANO, sia PARALLELA ad esso, basta che sia PARALLELA ad una
RETTA del PIANO .
Tutti i PUNTI di una RETTA PARALLELA ad un PIANO sono EQUIDISTANTI dal PIANO .
Se due PIANI sono PARALLELI ad un terzo sono PARALLELI fra loro .
Se due PIANI sono PARALLELI, il PIANO che INTERSECA l’uno deve INTERSECARE anche l’altro e le due
RETTE d’INTERSEZIONE risultano PARALLELE .
ANGOLI DIEDRI
Due SEMIPIANI uscenti da una stessa RETTA dividono lo spazio in due REGIONI. Ognuna di queste
REGIONI è detta ANGOLO DIEDRO .
La RETTA comune dicesi SPIGOLO o COSTOLA ed i due SEMIPIANI diconsi FACCE .
L’idea del DIEDRO ce la dà il libro semiaperto . Anzi il libro ci suggerisce come può immaginarsi generato un
DIEDRO .
Infatti il DIEDRO si può generare facendo ruotare un SEMIPIANO da una posizione di partenza e sempre
nello stesso senso .
Si avrà così, ad esempio, il DIEDRO PIATTO quando le due facce sono opposte e situate sullo stesso
PIANO; si avrà il DIEDRO GIRO quando la faccia ruotante sarà, appunto dopo un giro completo, tornata sulla
posizione di partenza . Come avete visto, ormai, gli ANGOLI DIEDRI ripetono nello spazio ciò che fanno gli
ANGOLI comuni nel PIANO .
Un DIEDRO si dice CONVESSO se non contiene i prolungamenti delle sue facce, altrimenti si dice
CONCAVO .
Valgono anche qui, le nozioni di DIEDRI CONSECUTIVI e ADIACENTI SUPPLEMENTARI e
COMPLEMENTARI, OPPOSTI allo SPIGOLO ecc., e le definizioni facili ad enunciarsi le lasciamo agli Allievi
veramente bravi e diligenti .
Si dice SEZIONE NORMALE di un DIEDRO l’ANGOLO PIANO intersezione del DIEDRO con un PIANO che
lo taglia perpendicolarmente alla COSTOLA .
Le SEZIONI NORMALI di uno stesso DIEDRO sono eguali .
A seconda dell’ampiezza della SEZIONE NORMALE abbiamo il DIEDRO RETTO, ACUTO ed OTTUSO .
Per misurare un DIEDRO se ne misura la SEZIONE NORMALE .
Come applicazione possiamo dire :
- due DIEDRI ADIACENTI sono SUPPLEMENTARI. Infatti, le SEZIONI NORMALI fatte con uno stesso
PIANO sono ANGOLI ADIACENTI e perciò SUPPLEMENTARI .
16/20
PIANI PERPENDICOLARI E PIANI PARALLELI
Due PIANI incontrandosi formano quattro ANGOLI DIEDRI a due a due OPPOSTI alla COSTOLA ed eguali
Due PIANI si dicono PERPENDICOLARI se intersecandosi formano quattro ANGOLI DIEDRI uguali,
necessariamente DIEDRI RETTI .
ANGOLOIDI
Se da un punto V dello spazio conduciamo tutte le SEMIRETTE congiungenti detto PUNTO con i punti
del contorno di un POLIGONO delimitiamo nello spazio una REGIONE detta ANGOLOIDE od ANGOLO
SOLIDO .
In essa le semirette diconsi SPIGOLI; gli ANGOLI piani si dicono FACCE e V, VERTICE comune a tutte le
FACCE, dicesi VERTICE dell’ANGOLOIDE .
Due FACCE vicine individuano un DIEDERO, perciò un ANGOLOIDE ha tanti DIEDRI quante FACCE, come
il POLIGONO aveva tanti ANGOLI quanti LATI .
Se le FACCE sono soltanto TRE l’ANGOLOIDE si dice TRIEDRO .
Cosicché nel TRIEDRO abbiamo tre SPIGOLI, tre FACCE, e tre DIEDRI le cui COSTOLE sono gli SPIGOLI
suddetti .
POLIEDRI
Dicesi P. un solido limitato da POLIGONI PIANI
Questi POLIGONI si dicono FACCE del P. ed i loro VERTICI ed i loro LATI, diconsi VERTICI e SPIGOLI del
P. .
Ogni SPIGOLO del P. è comune a due FACCE, mentre ogni VERTICE deve essere comune a non meno di
tre FACCE
Ogni SPIGOLO è la COSTOLA di un DIEDRO, ogni VERTICE è il VERTICE di un ANGOLOIDE .
Un P. non può avere meno di 4 FACCE .....
Il P. con 4 FACCE dicesi
Il P. con 5 FACCE dicesi
Il P. con 6 FACCE dicesi
Il P. con 7 FACCE dicesi
Il P. con 8 FACCE dicesi
Il P. con 9 FACCE dicesi
Il P. con 10 FACCE dicesi
Il P. con 11 FACCE dicesi
Il P. con 12 FACCE dicesi
Il P. con 15 FACCE dicesi
Il P. con 20 FACCE dicesi
TETRAEDRO ( ha 4 triangoli equilateri, 4 vertici e 6 spigoli)
PENTAEDRO
ESAEDRO
ETTAEDRO
OTTAEDRO
( ha 8 triangoli equilateri .... )
ENNAEDRO
DECAEDRO
ENDECAEDRO
DODECAEDRO o PENTA DODECAEDRO ( ha 12 pentagoni regolari .... )
PENTADECAEDRO
ICOSAEDRO ( ha 20 triangoli equilateri .... )
In effetti, però , eccetto alcuni dei suddetti nomi più adoperati si dice più comunemente :
POLIEDRO a 7 FACCE , di 11 FACCE, di 13 FACCE, ecc. .
Sviluppare un POLIEDRO significa, immaginandolo vuoto all’interno e fatto ad esempio di cartone, ritagliarlo
opportunamente lungo determinati SPIGOLI e stendere tutta la sua SUPERFICIE sul PIANO.
17/20
POLIEDRI REGOLARI
Un P. è regolare quando ha FACCE uguali, DIEDRI uguali ed ANGOLOIDI uguali .
I P. regolari sono soltanto cinque : il TETRAEDRO, l’ESAEDRO o CUBO, l’OTTAEDRO, il PENTAGONO
DODECAEDRO e l’ICOSAEDRO .
PRISMA
Il PRISMA è un P. limitato da due POLIGONI eguali, detti BASI, situati in PIANI PARALLELI e da tanti
PARALLELOGRAMMI, detti FACCE LATERALI, quanti sono i LATI di uno dei POLIGONI di BASE .
La somma delle SUPERFICI delle FACCE LATERALI si dice SUPERFICIE LATERALE del PRISMA .
Se alla SUPERFICIE LATERALE si aggiungono le SUPERFICIE delle DUE BASI, si ha la SUPERFICIE
TOTALE (abbreviandole in : Sl .... ed St ) .
Secondo che la BASE è un TRIANGOLO, un QUADRILATERO, ecc. il PRISMA si dice TRIANGOLARE,
QUADRANGOLARE, ecc.
Un PRISMA si dice RETTO se gli SPIGOLI LATERALI sono PERPENDICOLARI alle BASI, altrimenti si dice
PRISMA OBLIQUO ( o PRISMA NON RETTO) .
Un PRISMA si dice RETTO REGOLARE o semplicemente REGOLARE se è RETTO e la BASE è un
POLIGONO REGOLARE .
Si dice ALTEZZA di un PRISMA la distanza fra i PIANI delle BASI . Se il PRISMA è RETTO REGOLARE
l’ALTEZZA, condotta dal centro della BASE SUPERIORE passa per il centro del POLIGONO della BASE
inferiore .
Nel PRISMA REGOLARE RETTO l’ALTEZZA è uguale ad uno qualsiasi degli SPIGOLI LATERALI .
Un PRISMA particolare è il PARALLELEPIPEDO o ROMBOEDRO , il quale ha per BASE un
PARALLELOGRAMMA .
Il PARALLELEPIPEDO si dice RETTANGOLO o RETTOEDRO se tutte le FACCE sono dei RETTANGOLI .
Il CUBO od ESAEDRO è un POLIEDRO REGOLARE, è infatti un PARALLELEPIPEDO RETTANGOLO
particolare a FACCE tutte QUADRATE e perciò uguali .
Nel PARALLELEPIPEDO RETTANGOLO il QUADRATO costruito sulla diagonale è equivalente alla somma
dei QUADRATI costruiti sulle tre dimensioni .
PIRAMIDE
La P. è un POLIEDRO avente per BASE un POLIGONO e per FACCE LATERALI tanti TRIANGOLI che
convergono in uno stesso VERTICE detto VERTICE della PIRAMIDE .
La P. si può immaginare come ottenuta “ segando “ un ANGOLOIDE .
La P., come il PRISMA, prende nome dal POLIGONO di BASE .
Una P. si dice RETTA quando nel POLIGONO di BASE si può inscrivere un cerchio e l’altezza, condotta dal
vertice, passa per il centro di questo cerchio .
Una P. si dice RETTA REGOLARE quando il POLIGONO di BASE è REGOLARE e l’ALTEZZA passa per il
centro del POLIGONO .
18/20
Nella P. RETTA REGOLARE le FACCE LATERALI sono dei TRIANGOLI ISCOSCELI tutti eguali .
Si dice APOTEMA della PIRAMIDE RETTA REGOLARE l’ALTEZZA di una delle FACCE LATERALI .
N.B. : da non confondere questo APOTEMA con quello del POLIGONO di BASE . Il secondo è la proiezione
del primo, per cui si può notare che :
- altezza, apotema di base ed apotema laterale formano un triangolo rettangolo .
SOLIDI DI ROTAZIONE o ROTONDI
CILINDRO
Se immaginiamo che un rettangolo ABCD ruoti di un giro completo attorno al LATO AB, preso come asse
fisso di rotazione, il SOLIDO generato si dice : CILINDRO CIRCOLARE RETTO .
Il rettangolo ECDF che si ottiene sezionando il C. con un PIANO passante per l’asse AB (PIANO
MERIDIANO) dicesi SEZIONE MERIDIANA o PRINCIPALE del C. .
Un C. si dice EQUILATERO se la sua SEZIONE MERIDIANA è un QUADRATO .
Perciò nel C. equilatero il diametro di base è uguale all’altezza .
CILINDRO CIRCOLARE OBLIQUO, è sempre generato da un rettangolo (che ruota attorno ad un asse fisso)
e poi viene tagliato obliquamente (il rettangolo) . Un esempio è la TORRE di PISA .
Il C. obliquo sta all’impiedi se la perpendicolare condotta dal centro di gravità G sul piano orizzontale di base
cade dentro la base di appoggio .
CONO
Se immaginiamo che un TRIANGOLO RETTANGOO VOA ruoti di un giro completo attorno al cateto VO
preso come asse fisso di rotazione, il SOLIDO generato si dice CONO CIRCOLARE RETTO .
Il triangolo isoscele VAB che si ottiene sezionando il C. con un PIANO passante per l’asse VO (PIANO
MERIDIANO) dicesi SEZIONE MERIDIANA o PRINCIPALE del CONO .
Un C. si dice EQUILATERO se la sua sezione meridiana è un triangolo equilatero .
Nel C. EQUILATERO il diametro di base è uguale alla GENERATRICE od APOTEMA
CONO CIRCOLARE OBLIQUO, la SEZIONE MERIDIANA non è un TRIANGOLO ISOSCELE, ma qualunque
.
Se G è il centro di gravità il SOLIDO sta in equilibrio se la perpendicolare di G abbassata sul PIANO
orizzontale di BASE, cade dentro la base stessa .
19/20
SFERA
Se immaginiamo che un SEMICERCHIO di centro O e DIAMETRO AB ruoti di un giro completo attorno ad
AB, preso come asse fisso di rotazione, il SOLIDO generato si dice SFERA .
La SEMICIRCONFERENZA genera la SUPERFICIE della SFERA .
La SUPERFICIE SFERICA è l’insieme di tutti i punti dello spazio equidistanti da uno stesso punto detto
centro .
PARTI DELLA SFERA
Se si taglia la S. con un PIANO si ottiene per SEZIONE un CERCHIO e se il PIANO è DIAMETRALE, cioè
passa per il centro, la SEZIONE è un CERCHIO MASSIMO, il cui raggio, cioè, è quello della SFERA .
La Crf. del CERCHIO MASSIMO è detta Crf. MASSIMA od EQUATORE .
Un PIANO che taglia una S. la divide in due parti dette SEGMENTI SFERICI.
Se il PIANO è DIAMETRALE, i SEGMENTI SFERICI sono due SEMISFERE .
Un SEGMENTO SFERICO può avere due BASI ed in tal caso è il segmento compreso fra due PIANI
PARALLELI che tagliano la SFERA .
La parte di SUPERFICIE SFERICA appartenente ad un SEGMENTO SFERICO ad una BASE è detta
CALOTTA SFERICA .
Se il SEGMENTO SFERICO è a due BASI, la parte di SUPERFICIE SFERICA che gli appartiene è detta
ZONA SFERICA .
Si di ce SPICCHIO SFERICO, per analogia con lo spicchio di una arancia, la parte di S. compresa fra due
SEMIPIANI passanti per lo stesso DIAMETRO . In altri termini è la parte di SFERA compresa fra due
SEMICERCHI MASSIMI con DIAMETRO comune .
La SUPERFICIE SFERICA, a differenza delle altre SUPERFICI degli altri SOLIDI studiati fino ad ora,
NON SI PUO’ SVILUPPARE .
L’ area della SUPERFICIE SFERICA è uguale a QUATTRO VOLTE quella del CERCHIO MASSIMO .
ARCHIMEDE (determina l’Area della Superficie Sferica con metodo mirabile)
A. dimostrò che : l’AREA della SUPERFICIE SFERICA è uguale a quella LATERALE del CILINDRO
EQUILATERO CIRCOSCRITTO .
S = 4 *
* r
2
Si narra che tale disegno venne scolpito sulla tomba del grande matematico siracusano .
Gorizia lì, 14 settembre 2009
Il Docente
prof. Maurizio VISINTIN
20/20