m.c.m. (minimo comune multiplo) tra due numeri

m.c.m. (minimo comune multiplo) tra due numeri
Un numero intero positivo ha un numero infinito di multipli.
Esempio 1:
I multipli del 5 sono 5, 10, 15, 20, 25, 30, 35, ..., 70, ..., 105, 110, ..., 140, ... (e così via)
I multipli del 7 sono 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, ..., 105, 112, 119..., 140, ... (e così via)
In grassetto sono evidenziati I primi 6 numeri che sono multipli sia del 5 che del 7 (I multipli in comune
sono infiniti).
Il minimo comune multiplo (indicato con m.c.m.) tra due numeri è il più piccolo fra I multipli comuni. Il
minimo comune multiplo tra il 5 e il 7 è il 35.
Esempio 2:
Determinare qual è il m.c.m. tra I numeri 4 e 18.
I multipli del 4 sono 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, ...
I multipli del 18 sono: 8, 36, 54,72, 90, ...
Sono stati evidenziati I primi 2 multipli comuni ad entrambi (36 e 72). Il m.c.m. è il più piccolo fra questi,
ossia il 36.
Poiché il m.c.m. deve essere un multiplo di entrambi I numeri, sarà sempre maggiore o uguale al maggiore
tra I due numeri.
Rappresentazione grafica.
Si può immaginare che i due numeri rappresentino le lunghezze di due asticelle di legno (in metri, cm,
“tacchette”, non ha importanza quale unità di misura si considera). Determinare il m.c.m. significa allora
trovare la lunghezza della più piccola asticella che contenga un numero intero di volte sia la prima
asticella che la seconda.
Se, come nell’esempio 2, le asticelle sono lunghe rispettivamente 4 e 18 “tacchette”, le possiamo
disegnare in questo modo:
Una asticella lunga quanto la seconda contiene, ovviamente, un numero intero di volte la seconda (una
volta), ma non la prima (avanzano infatti 2 “tacchette”). Allora dobbiamo considerare una asticella lunga il
doppio della seconda:
Questa contiene 2 volte l’asticella più lunga e 9 volte quella più corta:
Come determinare il minimo comune multiplo fra due numeri?
Si può procedere in due modi:
1. Si parte dal numero più grande e si considerano via via i suoi multipli. Ci si ferma quando si trova un
numero che è multiplo anche del numero più piccolo.
Nel primo esempio (con I numeri 5 e 7) si parte dal numero 7 (7∙1=7);
•poiché 7 non è multiplo del 5 si passa al multiplo successivo del 7, ossia il 14 (7∙2=14);
•neanche questo è multiplo del 5 e si passa al successivo multiplo del 7, ossia al 21 (7∙3=21);
•neanche questo va bene e si passa al successivo, 28 (7∙4=28);
•neanche questo va bene e si passa al successivo, 35 (7∙5=35).
•Questo è anche un multiplo del 5 quindi è proprio il m.c.m.
Nel secondo esempio (con I numeri 4 e 18) si parte dal numero 18 (18∙1=18);
•poiché 18 non è multiplo del 4 si passa al multiplo successivo, ossia al 36 (18∙2=36).
•Poiché 36 è anche multiplo del 4 significa che 4 è proprio il m.c.m.
2. Esiste un procedimento più rigoroso che consiste nello scomporre i numeri in fattori primi; poiché si
cerca il più piccolo multiplo che sia comune ad entrambi, si calcola il prodotto dei fattori comuni e non
comuni dei due numeri.
Ovviamente, se un numero compare come fattore comune ripetuto, ossia compare sottoforma di potenza,
e le potenze non hanno lo stesso esponente, si considera la potenza con esponente maggiore.
Nel primo esempio 5 e 7 sono già scomposti (sono numeri primi). L'unico fattore comune è 1, mentre sia 5
che 7 sono fattori non comuni e vanno considerati entrambi. Il m.c.m. è quindi 5∙7=35.
Nel secondo esempio, scomponendo 4 e 18 si ottiene:
4= 22 ; 18= 2∙32
L'unico fattore comune è il 2 che compare però 2 volte nel 4 (come 22); quindi si considera sia il 2 che è
comune sia l'altro fattore 2 che compare solo nel 4, quindi si considera 22; l'altro fattore non comune è 32.
In definitiva il m.c.m. è dato da 22∙32 ossia 36.
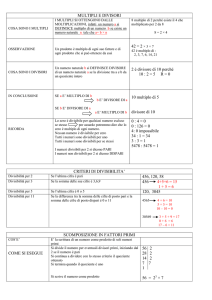
Esempi:
1° numero=scomposizione 2°numero=scomposizione
m.c.m.
4 = 22
10 = 2∙5
22∙5=20
4 = 22
8 = 23
23=8
24 = 23∙3
32 = 25
25∙3=96
10 = 2∙5
20 = 22∙5
22∙5 = 20
4 = 22
18 = 2∙32
22∙32 = 36
M.C.D. (Massimo Comune Divisore) tra due numeri
Un numero intero può avere diversi divisori (oltre al numero stesso e al numero 1).
Per esempio:
i divisori del 10 sono il 2 e il 5;
i divisori del 18 sono il 2, 3, 6, 9
i divisori del 24 sono il 2, 3, 4, 6, 8, 12
Due numeri possono avere dei divisori in comune. Per esempio, il 18 e il 24 hanno in comune il 2, 3, 6.
Il Massimo Comune Divisore (indicato con M.C.D.) tra due numeri è il più grande fra i divisori comuni. Il
M.C.D. tra 18 e 24 è perciò il 6.
Poiché il M.C.D. deve essere un divisore di entrambi I numeri, sarà sempre minore o uguale al minore tra i
due numeri.
Rappresentazione grafica
Si può immaginare che i due numeri rappresentino le lunghezze di due asticelle di legno (in metri, cm,
“tacchette”, non ha importanza quale unità di misura si considera). Determinare il M.C.D. significa allora
trovare la lunghezza della più grande asticella che sia contenuta un numero intero di volte sia nella prima
asticella che nella seconda.
Se, per esempio, le asticelle sono lunghe rispettivamente 18 e 24 “tacchette” le possiamo disegnare in
questo modo, evidenziando i vari divisori, ossia le parti (uguali) in cui possono essere suddivise le due
asticelle. I punti corrispondenti a tagli di 6 tacche corrispondono anche a tagli di 2 tacche e di 3 tacche
(nel disegno le linee sono sovrapposte)
Entrambe le asticelle possono essere divise in tagli lunghi 2, 3 e 6 tacche.
Il taglio più grande che divide entrambe le asticelle in parti uguali è lungo 6 tacche. Quindi 6 è il M.C.D. Tra
18 e 24
Come determinare il Massimo Comune Divisore fra due numeri?
Poiché si cerca un divisore che sia comune ad entrambi e che sia il più grande, si scompongono i numeri in
fattori primi e si calcola il prodotto dei soli fattori comuni ad entrambi i numeri.
Ovviamente, se un numero compare come fattore comune ripetuto, ossia compare sottoforma di potenza,
e le potenze non hanno lo stesso esponente, si considera la potenza con esponente minore.
Esempi:
1° numero=scomposizione 2°numero=scomposizione
M.C.D.
4 = 22
10 = 2∙5
2
4 = 22
8 = 23
22=4
24 = 23∙3
32 = 25
23=8
10 = 2∙5
20 = 22∙5
2∙5 = 10
4 = 22
18 = 2∙32
2
m.c.m e M.C.D. tra polinomi
La prima cosa da fare è scomporre i polinomi in fattori irriducibili, e questo è un problema che va
affrontato a parte.
Supposto che i polinomi siano scomposti, è necessario innanzitutto capire bene quali sono i fattori.
Esercizio: evidenziare i vari fattori dei seguenti polinomi (già scomposti)
a) 4(x+1)(y+3)(y2+1)
i fattori sono: 4, (x+1), (y+3), (y2+1)
b) 3x2(y2+1)
i fattori sono: 3, x2, (y2+1)
c) 3x2+1
c’è un unico fattore che è (3x2+1)
d) (3x2+y+1)(y2+1)
i fattori sono: (3x2+y+1) e (y2+1)
Attenzione: Nel caso c) 3x2 e 1 sono legati dal segno di addizione, non dal segno di moltiplicazione, quindi
sono addendi, non fattori.
Negli altri casi, invece, i vari “pezzetti” sono legati dal segno di moltiplicazione e, per esempio, nel caso d)
tutto il polinomio (3x2+y+1) è uno dei fattori e tutto il polinomio (y2+1) è l’altro fattore.
Per il calcolo del m.c.m. e del M.C.D. si procede con un ragionamento analogo a quello fatto
precedentemente nel caso dei numeri, ossia:
• per il m.c.m. si considera il prodotto dei fattori comuni e non comuni dei polinomi (con le stesse
osservazioni fatte a proposito delle potenze)
• per il M.C.D. si considera il prodotto dei fattori comuni dei polinomi (con le stesse osservazioni
fatte a proposito delle potenze)
Esempi
m.c.m. e M.C.D. tra diverse terne di polinomi (i polinomi sono già stati scomposti in fattori irriducibili):
1°polinomio
2°polinomio
3°polinomio
m.c.m.
M.C.D.
(x-4)(x+4)
4(x-4)
(x-4)2
4(x-4) 2 (x+4)
(x-4)
3(x+y)
x(x+y)
5(x - y)
15x(x+y)(x-y)
1
3(x-y)
x(x-y)
5(x - y) 2
15x(x-y) 2
(x-y)